履带起重机拉管结构流固耦合数值分析

奚传峰 高顺德 徐金帅 孙丰科 郭二棒

1大连理工大学机械工程学院 大连 116025 2大连理工大学工程力学系 大连 116025

0 引言

随着基础工程建设的不断发展，大吨位履带起重机不断出现，其臂架组合总高度达到200 m以上，作为重要连接部件的拉管结构也随之变得细长、轻柔。拉管结构的自振频率低，属于风载荷敏感性较强的大跨度柔性结构，在风载荷作用下易产生较大振动和变形，且强烈的振动会导致拉管结构的固结处发生疲劳破坏[1]。

对于工程中的拉管以及与拉管类似的拉索系统，国内外学者均有研究，王春江等[2]研究了长单索结构的风载荷响应现象，对比采用传统单索动力学计算方法和采用流固耦合方法的计算结果，发现考虑流固耦合效应得到的风压峰值比传统计算方法得到的值大15%～20%；Liu M M等[3]利用数值计算的方法对间距不同的并列拉索进行研究，得出风载荷对不同间距拉索结构的动力系数和静力系数的影响；刘庆宽等[4]采用风洞实验的方法针对并列拉索出现的尾流涡激振动现象进行研究，得到尾流涡激振动现象产生时的升力和阻力系数；杜晓庆等[5]研究了不同风攻角对串联和错列拉索的影响，提出了增加阻尼比来解决下游拉索出现的涡激共振问题；孙亭亭等[6]对脉动风条件下近距离并列拉索进行数值分析，分析上游拉索对下游拉索周围流场的影响，得出上游拉索出现的圆柱绕流现象使下游拉索的流场变得更加复杂。通过理论分析、风洞试验、数值分析等方法对拉索等大跨度柔性结构风载荷响应的作用机理、发生条件及影响因素等做了大量研究。从研究结果看，学者们对履带起重机中的拉管结构的研究较少。鉴于此，本文采用计算流体力学（Computational Fluid Dynamics，CFD）的方法，应用Ansys Workbench软件对拉管结构和流场进行双向流固耦合数值计算，分析拉管结构周边流场的压力分布以及结构的风载荷响应，并与GB/T 3811－2008《起重机设计规范》[7]中的计算结果进行对比，为履带起重机拉管结构的工程设计与计算提供参考。

1 数值分析模型

1.1 模型建立

如图1所示，以660 t履带起重机塔臂后拉管结构作为研究对象，拉管结构由不同规格尺寸的拉管通过销轴连接而成。为了避免在数值分析过程中出现网格数量多、网格形状畸形、计算数据过大而导致计算过程中出现错误，在保留拉管结构主体特征的基础上，忽略拉管连接处的复杂曲面，对模型进行简化。利用SolidWorks按1:1参数比例建立拉管三维实体模型，拉管结构模型高为36 m，外径D为0.14 m，内径d为0.11 m，2个拉管中心距L为2.8 m。

图1 660 t履带起重机塔臂后拉管结构示意图

1.2 计算域与网格模型

在ICEM CFD中建立拉管结构的流场计算域，并采用结构化网格划分。计算域采用长方体，上游来流为40D，下游为50D，宽为40D，中心距L为20D，计算域二维示意图如图2所示。

图2 计算域二维示意图

为了能够简易、高效、精确模拟出拉管在实际工程环境下的风载荷，利用O-Block方法进行结构化网格划分，并在流固场接触面进行加密处理，如图3所示。为尽可能模拟拉管外部无限大的流场环境，降低流场边界对分析结果的影响，计算域的阻塞率为2.5%，满足阻塞比小于3%的要求。计算域网格划分完成后，节点数为7 160 362，网格数量为7 399 512。

图3 网格模型划分示意图

1.3 湍流模型

拉管结构主体特征为圆管，在风流经拉管表面时会产生钝体绕流效应，进而出现旋转和分离流动现象。计算域流场为完全发展的湍流流场，所以选用适用于湍流发展非常充分并具有稳定性好、计算精度较高等优点的Standardκ-ε模型。

1.4 边界条件设置

1）入口为速度进口边界条件，由于边界条件较复杂，无法通过Fluent标准界面直接完成，故用户可采用自定义函数（User Defined Functions，UDF）实现。

2）为了能够实现更好的收敛，出口为压力出口边界条件。

3）除拉管模型表面和地面采用无滑移壁面条件，其他面均为对称面条件，用来模拟无限大空间流场。

4）采用Simplce算法对速度-压力耦合方程进行求解，离散格式采用二阶迎风格式，收敛残差均采用默认值为10-3，并监测进出口质量流量，不平衡误差为0.000 3%，满足小于0.1%的收敛要求。

2 计算结果分析

数值模拟在Ansys Workbench平台上进行，模拟20 s拉管结构与流场双向耦合过程，利用Fluent模块进行流场计算，得到流场的压力分布情况，分析拉管结构附近的流场在不同高度处的压力变化情况；利用Transient Structural模块进行结构分析，得到拉管结构的风载荷响应曲线，分析拉管结构在风场中的风载荷响应。

2.1 流场分析

为了描述不同高度时拉管结构周围流场压力场和压力分布情况，将其分成4段研究，高度分别为9 m、18 m、27 m和36 m，并分析压力变化明显的局部流场区域，绘制出图4～图11所示不同高度的压力分布云图和流固交界面上的周向压力，图中白色区域为拉管结构，来流风从左侧流入右侧流出，按照风先后流经的顺序，左侧为前拉管，右侧为后拉管。

图4 9 m高度前后拉管的压力云图

图5 9 m高度前后拉管的周向压力

图6 18 m高度前后拉管的压力云图

图7 18 m高度前后拉管的周向压力

图8 27 m高度前后拉管的压力云图

图9 27 m高度处前后拉管周向压力

图10 36 m高度前后拉管的压力云图

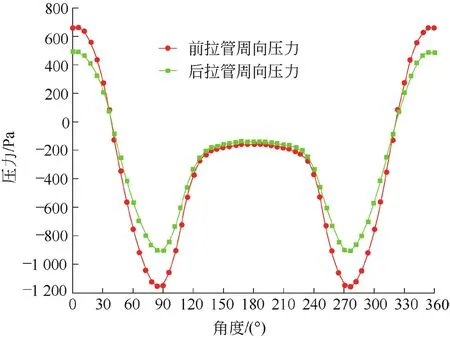
图11 36 m高度前后拉管的周向压力

由图4～图11可知，前后拉管的最大正压力值出现在结构迎风面的最前端，最大负压力值出现在结构两侧的位置；对比前后拉管在同一高度时的周向压力，可以看出前后拉管的周向压力变化趋势相同且对称分布；在同一高度时，前拉管的最大正压力和最大负压力的绝对值都大于后拉管的最大正压力和最大负压力的绝对值。

对同一拉管在不同高度时拉管结构表面的周向压力进行比较，如图12所示。从图中可以看出，前后拉管的最大压力值随拉管高度的增加而增大，前后拉管的最大负压力值随拉管高度的增加而减小；拉管后面形成的负压区压力均值也随高度的增加而减少，其变化值小于最大负压力的变化值。

图12 前后拉管不同高度时的周向压力

根据GB/T 3811－2008《起重机设计规范》，通过在风压计算公式中引入风压高度变化系数来处理风载荷高度变化引起的影响，将规范与数值计算得到的最大正压力结果做对比，得到表1、图13所示结果。

表1 最大正压力数值计算结果与规范比较

图13 不同高度最大正压力值比较

由图13可知，最大正风压力数值随高度的增加而不断增大，数值计算结果和规范结果比较接近，但规范值比数值计算结果略大，这是因为规范中将风载荷当作静载荷处理，为了使公式结果达到真实风载荷大小，对各参数的取值偏大相对保守。在实际工程中，由于存在钝体绕流、拉管结构背风面有旋涡产生、出现局部回流、风速减小等情况，使得风载荷局部损失增大，同时也是造成同一高度时前拉管最大正压力大于后拉管最大正压力的主要原因。

2.2 拉管结构分析

大气边界层中的自然风由平均风和脉动风组成，在GB/T 3811－2008《起重机设计规范》中将结构风载荷按照平均风载荷处理，未考虑到自然风中脉动风对结构的动力作用。通过双向流固耦合数值分析，可得到拉管结构在流场中的风载荷响应现象，如图14所示。

图14 前后拉管顺风向位移

由图14可知，前后拉管在风载荷作用下均出现了风致振动现象，并在结构阻尼作用下先后变成周期性振动。对比前后拉管顺风向位移曲线，可知前拉管平均位移略小于后拉管的平均位移，前拉管振动频率比后拉管振动频率大，前拉管振幅比后拉管的振幅大，后拉管比前拉管更快进入稳定振动周期。

对前后拉管顺风向振动进行频谱分析，由图15可以看出引起振动的频率成分有很多，其中频率较低的部分是结构所受阻力的频率，另一个为0.65 Hz的卓越频率接近前后拉管的自振频率（0.62 Hz），同时也是引起前后拉管强迫振动的主要原因。对比前后拉管的频谱可知，频率为0.60～0.80 Hz区间时前后拉管在相同频率上出现幅值差异，主要原因是风流经前拉管时出现圆柱绕流现象，使得后拉管的上游风场出现扰动，进而使该范围内的周期成分得到削弱或增强。因此，可以通过在拉管上分段布置小的连接结构改变拉管结构的固有频率，减少风对拉管结构的影响。

图15 前后拉管顺风向位移频谱

3 结论

本文以实际工程背景为依托，基于计算流体力学对拉管结构进行双向流固耦合数值分析，并采用计算精度较高，稳定性较好、经济性较高的Standard 湍流模型，研究拉管结构在风载荷作用下的风载荷响应特性以及不同高度处流场分布，基于数值计算结果得出以下结论：

1）将拉管结构附近的流场分成4段进行研究分析发现，前后拉管的最大压力值随拉管度的增加而增大，前后拉管的最大负压力值随拉管高度的增加而减小；

2）前后拉管的周向压力变化趋势相同，最大压力均出现在拉管迎风的最前段，最大负压出现在拉管结构的两侧；

3）将规范计算的结果与数值计算得到结果做对比发现，两者比较接近，但由于GB/T 3811－2008《起重机设计规范》中将风载荷当作静载荷处理，为了使公式结果达到真实风载荷大小，对各参数的取值偏大，使得规范值比数值计算结果略大。

4）将前后拉管顺风向位移进行频谱分析发现，来流风中的频率成分主要集中分布在0.60～0.80 Hz，而前后拉管的固有频率也在此范围内，这是引起前后拉管强迫振动的主要原因。所以，在履带起重机拉管结构设计中，应考虑在拉管上分段布置小的连接结构来改变拉管结构的固有频率，减少风载荷响应引起的振动。