基于改进多维规划的生产材料智慧订购问题研究
2022-06-11李景晗任桓君陈晓艺王丽莎
李景晗 任桓君 陈晓艺 王丽莎
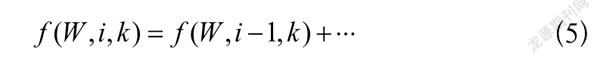
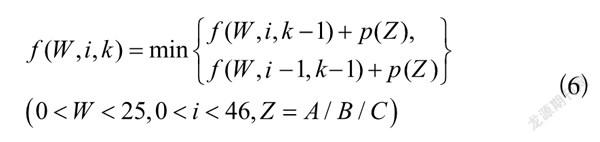

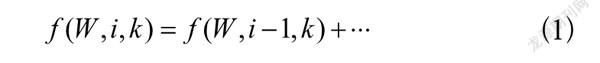
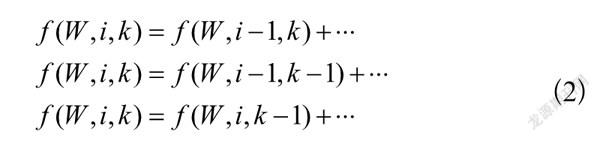

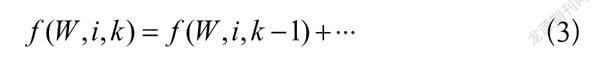
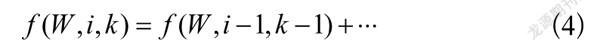
摘 要:目前,在解决生产型企业对多个供应商的最佳订购方案进行选取问题时,通常使用多目标规划或遗传算法。这些方法效率普遍不高,尤其是对复杂问题求解耗时很长。为提高求解效率,提出一种基于改进多维动态规划的智慧订购方案求解方法,该方法以最小生产成本为目标,通过约束最低生产需求和最大供货量,建立从二维延展至三维的动态规划模型,再对三维模型进行简化求解。通过实例验证了该方法的可行性和有效性。对比遗传算法,改进多维动态规划在运行效率和模型简练度上有很大优势。
关键词:动态规划;材料订购;方案决策;多维规划
中图分类号:TP31 文献标识码:A
Research on Intelligent Ordering of Production Materials
based on Improved Multi-dimensional Planning
LI Jinghan REN Huanjun CHEN Xiaoyi WANG Lisha
Abstract: At present, multi-objective planning or genetic algorithm is usually used by production enterprises to solve the problem of selecting the best ordering plan when facing multiple suppliers. These methods are generally inefficient and take a long time especially for solving complex problems. In order to improve the solution efficiency, this paper proposes an intelligent ordering plan solution based on improved multi-dimensional dynamic planning. Taking minimum production cost as the goal, This solution establishes a dynamic planning extending from 2D to 3D by constraining minimum production demand and maximum supply quantity, and then simplifies the solution of the 3D model. The feasibility and effectiveness of the proposed method are verified by an example. Compared with genetic algorithm, the improved multi-dimensional dynamic planning has great advantages in operation efficiency and model simplicity.
Keywords: dynamic planning; material ordering; plan decision; multi-dimensional planning
1 引言(Introduction)
為了满足生产需求和把控供应链风险,部分生产型企业采用多供应商供货、多次少量订购的策略采购生产材料。如果对原材料的订购工作缺乏足够重视,可能会导致生产活动受到严重影响[1]。目前在解决生产型企业对多个供应商的最佳订购方案进行选取问题时,通常使用多目标规划或遗传算法[2-3]。这些方法虽然可以得出订购方案,但解决复杂问题需要大量计算时间。面对这一问题,改进的动态规划模型脱颖而出。在这类单生产企业、多供应商的情景下,已经有郑广珠等[4]提出了遗传算法和动态规划的双层规划方法。考虑到传统的动态规划算法无法解决这类复杂问题,我们将传统的动态规划模型从二维延展至三维,再对三维模型进行简化求解。相较于其他方法,该方法具有高效、简洁、逻辑明晰的特点。
2 问题描述(Problem description)
企业每周的产能为2.82万立方米,每立方米产品需消耗甲类原材料0.6 立方米,或乙类原材料0.66 立方米,或丙类原材料0.72 立方米。原材料的采购成本直接影响企业的生产效益,实际中甲类和乙类原材料的采购单价分别比丙类原材料高20%和10%。在生产活动中,供应商的数量往往较多,现有50 个以订购欲望为目标排序的供应商,需要根据实际情况预测企业在未来24 周的订购方案。考虑到在实际情况中,单个供应商的供应能力会随时间改变,所以设定每个供应商的供货能力、企业仓库存货的数量以及企业生产材料的需求量等因素会随着周数W的增加而不断变化。可以从任意供应商订购生产材料,订购周期为每周一次。
为了解决上述问题,本文提出了一种基于改进动态规划的生产材料订购决策方法。
3 简化的三维供应商选取动态规划模型(Simplified dynamic planning model of 3D supplier selection)
3.1 模型建立
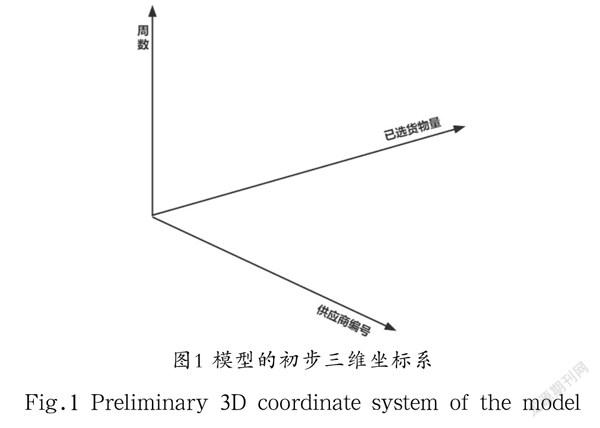
传统的动态规划大多是在二维状态变量上实现的,但此问题拥有周数、供应商编号、材料的购置数量三个状态变量,二维模型不能解决该问题。要将模型扩展至三维,就需要引入时间变量作为第三个维度,即以周数、供应商编号、已选货物量为三维的坐标系,如图1所示。
3.2 模型简化
由于三维状态变量的动态规划在本问题下求解复杂,不宜直接使用。先在时间不变的前提下,建立以已选货物量、供应商编号为状态的二维动态规划,当求得该天在满足约束条件后成本的最小值时,将周数W加1,重新进行本次动态规划,从而将三维状态变量的动态规划简化为多个二维状态变量的动态规划。
3.3 模型定义
(1)动态规划原问题
针对选出的50 个供应商,给出未来24 周企业最经济的材料订购方案。
(2)动态规划子问题
针对选出的50 个供应商,给出未来第W 周企业最经济的材料订购方案。
(3)定义状态
为未来W 周的最小成本,i为供应商编号,k为企业目前已选货物量。尤其当
(1)
时就是要求解的原问题。
4 基于改进动态规划决策模型的实现(Realization of decision model based on improved dynamic planning)
4.1 状态转移方程约束条件的分析
本问题主要存在两个约束,分别为生产需求的约束和最大供货量的约束。其中,生产需求的约束要求为:如果目前已经选择的货物足够满足本周生产需求,那么就不必再购买其他材料;最大供货量的约束要求为:如果某家供应商达到了最大供货量,那么不能在此供应商处继续购买,强制转移到下一家供应商。
4.2 二维部分的DP数组状态更新
当W固定时,在二维数组中进行状态更新,如图2所示。此时,状态更新一般具有三种方式[5]:
(2)
在本情景中:
(3)
表示从供应商i处购买一个货物。
(4)
表示更改至下一个供应商并且购买一个货物。
(5)
表示转到下一个供应商但没有购买任何货物。由于要进行择优购买,因此当出现这种情况时即表示满足约束,跳转至。因此最后一种状态转移是不存在的。
由于在更新初始点的状态时数组中不存在任何有效数值,此时无状态转移关系,因此要对其进行单独赋值。尤其是当时,状态位于边界,因为此时的状态只能从上方转移而来,要对其进行特殊考虑。
4.3 三维部分的DP数组状态更新
当满足的约束条件时,周数要进行至 周,同时进行下一时间段的状态更新,更新原理与4.2部分同理。
由此得到的状态转移方程为:
(6)
其中,表示供应商提供的材料的单价,A、B、C代表不同优先级的供应商。
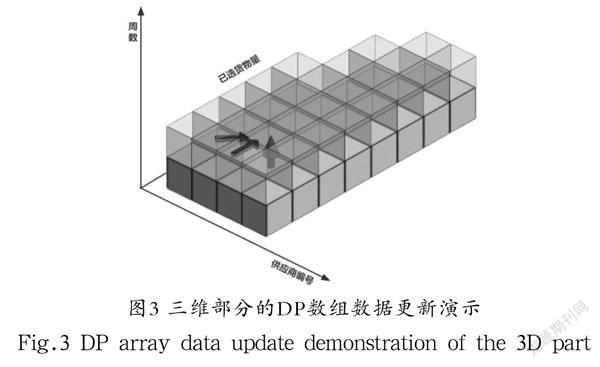
该动态规划的流程图如图3所示。
5 程序设计实现(Program design and implementation)
在实际编程的状态转移过程中,除了要考虑状态转移方程和约束条件,还需要考虑其他一系列量的变化,主要包括上一状态的位置信息、已选择货物的总生产量、此状态累计各供应商供货量。在每次状态更新时需要同步更新信息,由于程序采用了结构体的数据存储方式,可以方便地实现上述过程。
如果状态转移方程的前者为最小值,则用的值更新上一状态的位置信息;用状态的货物总生产量与目前购买商品可生产量之和更新已选择货物的总生产量;通过自增目前供应商对应的存储量来更新累计各供应商供货量。
如果后者为最小值,则用的值更新上一状态的位置信息;用状态的货物总生产量与目前购买商品可生产量之和更新已选择货物的总生产量;通过自增目前供应商对应的存储量来更新累计各供应商供货量[6-7]。
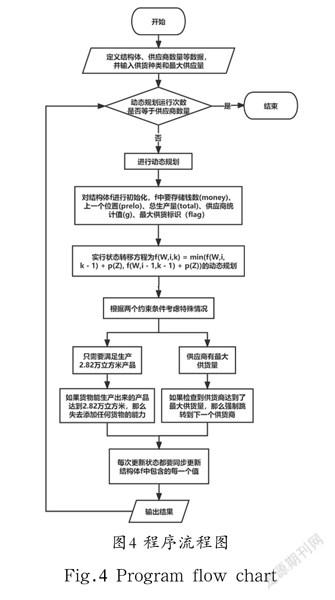
程序流程图如图4所示。
6 结果分析(Result analysis)
将实验所用的24 家运营商的数据分析带入,为该企业制定未来24 周每周最经济的原材料订购方案,并记录程序运行时间。程序运行结果中的每一行代表一周,每一列代表一个供应商,数字表示这一周该供应商的采购量。由于数据量过大,仅展示某次运行的部分结果,如图5所示。
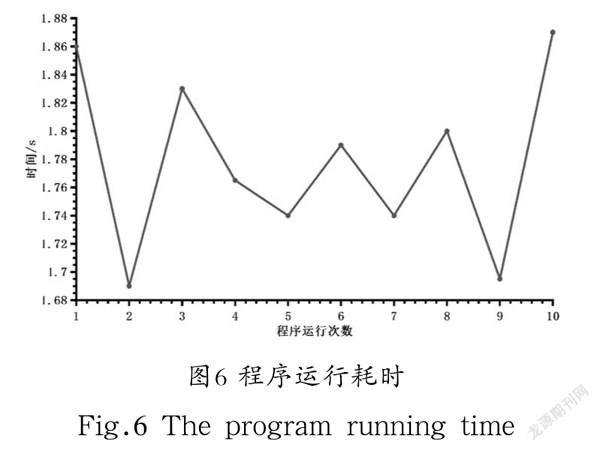
图6为程序运行十次的时间记录。
程序平均运行时间为1.778 秒,且浮动不显著。前文提到,本文提出的模型需要解决的一个重要问题就是节约时间,这也是本文提出方法的目的之一。对比雷绍雍等[8]的基于遺传算法的装备采购决策模型,本文方法的程序运行效率有很大优势。从本文的论述过程中可以看出:本文模型具有结构简练、冗余少和逻辑清晰的特点。
这项成果不但可以帮助生产型企业在快节奏、短周期的生产活动中快速做出订购决策,还有利于加强企业对供应链的把控,减少风险,调高抵御风险的阈值,最终增加利润。
7 可使用场景及优势分析(Available scenarios and advantage analysis)
7.1 无人零售
无人零售领域的核心企业能否高效整合无人零售终端的供应链网络,既影响着消费者的购物体验,也影响着无人零售模式的长远发展[9]。但无人零售终端往往使用低性能的设备,比如自动柜员机、自动售货机等,机器性能的局限导致无人零售终端很难使用复杂模型预测供货。本模型先通过现有技术检测每个货物的库存量和消耗量,再输入针对使用场景的定制程序。程序可以快速计算出补货需求和补货时机并反馈给维护人员。生产材料智慧订购模型的高效性和低性能要求可以避免因为设备性能低导致的宕机。这项应用也有利于无人零售终端的供应链资源整合优化。
7.2 医药采购
目前在我国基层药店,有时由于供应采购不及时会发生药品短缺的情况。生产材料智慧订购模型可以平衡需求量、积压量和保质期三者的关系,达到药店利益最大化,病人也可以及时足量地购买药品。这其实也可以为医药采购云平台的实现[10]奠定基础。
7.3 中小制造业辅助决策
新型冠状病毒肺炎疫情对我国的制造业造成了一定影响,对生产型企业提出了新的要求。生产型企业要生存,就必须抛弃原先的粗放式经营概念,对供应链和库存的把控要更加精准,建立更加科学的供应体系。这就必然要解决生产材料的订购决策问题。针对中小型企业往往难以负担大型运算设备,并且订购决策具有较大的即时性,生产材料智慧订购模型可以很好地完成这项需求。
7.4 其他应用
生产材料智慧订购模型的应用是非常广泛的,除了上文提到的场景外,还可以在智慧农业、小微快餐食品行业等场景中发挥作用。
8 结论(Conclusion)
针对生产型企业的生产材料智慧订购问题,本文提出了基于改进多维规划的解决方法。先建立从二维延展至三维的动态规划模型,再对模型做出局部简化。该模型在运算单供货商及24 家供货商且供货量随时间变化的复杂情景中,其程序平均运行时间为1.778 秒。实验结果直接体现出该方法的高效性。由于条件限制,本文取得的企业数据是有限的,要证明算法的普适性还需要进一步的研究。
参考文献(References)
[1] 冯瑞华,万勇.欧盟关键原材料需求与供应风险分析[J].新材料产业,2021(1):20-23.
[2] 钟映竑,张培新.基于FTOPSIS和模糊多目标规划的多产品低碳供应商选择方法研究[J].科技管理研究,2014,34(22):
223-226.
[3] 魏萌.基于改进遗传算法的原材料智能采购系统的研究与实现[D].沈阳:辽宁大学,2021.
[4] 郑广珠,杨晓英,张瑞敏,等.基于双层规划的多供应商物料配送期量优化[J].计算机应用与软件,2021,38(7):87-92.
[5] BELLMAN R. The theory of dynamic programming[J]. Bulletin of the American Mathematical Society, 1954, 60(6):503-515.
[6] HOWARD R A. Dynamic programming[J]. Management Science, 1966, 12(5):317-348.
[7] HO W, XU X, DEY P K. Multi-criteria decision making approaches for supplier evaluation and selection: A literature review[J]. European Journal of Operational Research, 2010, 202(1):16-24.
[8] 雷绍雍,刘靖旭.基于遗传算法的装备采购决策优化研究[J].中國管理科学,2020,28(10):194-200.
[9] 锁立赛,姚建明,周佳辉.基于顾客需求偏好的面向无人零售终端的供应链资源整合优化研究[J].中国管理科学,2021,
29(10):84-95.
[10] 孙朋.基于SaaS模式的医药采购云平台设计与实现[D].南京:东南大学,2019.
作者简介:
李景晗(2001-),男,本科生.研究领域:计算机与决策分析.
任桓君(2001-),男,本科生.研究领域:土木工程.
陈晓艺(2001-),女,本科生.研究领域:管理科学与工程.
王丽莎(1980-),女,博士,副教授.研究领域:微分方程及其数值离散系统的动力学性质研究.本文通信作者.
