带误差的等式约束优化问题的BFGS-SQP-L方法分析
2022-06-10周永辉
武 听,周永辉
(1.贵州师范大学 数学科学学院,贵州 贵阳 550025;2.贵州师范大学 大数据与计算机科学学院,贵州 贵阳 550025)
0 引言
BFGS方法是求解无约束优化问题的拟牛顿法中最有效的方法之一,由Broyden[1],Fletcher[2],Goldfarb[3]和Shanno[4]提出。其经典的收敛分析是在假定目标函数及其梯度是精确的情况下进行的,结果表明该算法具有很好的数值效果和快速的收敛效果。目前BFGS被认为是迄今最好的拟牛顿公式[5],并成为工程师和数学家解决最优化问题的主要方法。关于等式约束优化问题,Fukushima[6]提出序列二次规划(SQP)方法,成为解决约束优化最有效的数值算法之一。而对于二次规划子问题有许多求解方法,如BFGS-SQP法、Powell-SQP法、PSB-SQP法以及Salsa-SQP法等[7-8]。
但是随着社会的发展,一些无法精确估计目标函数和梯度的现实优化难题摆在眼前,如机器学习和函数评估容易受到计算误差影响的模型。因此,人们开始研究带误差问题的优化算法及其理论性质和实际性能。Choi等[9]和Kelley[10]针对不精确梯度的BFGS方法采用了隐式滤波法,该方法假设噪声可以在任何迭代中随意减小,通过确保噪声随着迭代接近解而衰减,保证了该方法的收敛性。Dennis等[11]和Ypma[12]研究了带误差的拟牛顿法的有界变差性质和局部收敛性,当在解附近开始时,Hessian近似接近精确的Hessian近似。Barton[13]提出了BFGS方法的一种实现方式,其中假设函数中的噪声是已知的,通过适当的有限差分技术来计算梯度。Berahas等[14]使用Hamming的有限差分技术估计函数中的噪声,并使用这种估计来计算BFGS方法中的有限差分梯度,其中将噪声考虑在内并放宽了Armijo条件,但没有研究噪声对BFGS更新的影响。Xie等[15]在文献[13]的基础上,保留了标准的Armijo-Wolfe线搜索,提出了目标函数和梯度存在误差的无约束优化问题的BFGS算法,证明了所提出的算法是局部线性收敛的。
本文在文献[1-4,6-13]基础上,针对目标函数及其梯度均有误差的等式约束优化问题,给出BFGS-SQP-L优化算法。其主要方法是将经典的BFGS公式嵌入到序列二次规划(SQP)框架,采用拉格朗日(L)步长,并应用延长差分技术以保证算法的可行性。最后,我们将考虑目标函数及其梯度估值的误差是一致有界的情形,研究所提出的BFGS-SQP-L优化迭代算法的局部收敛性。
1 等式约束优化问题
考虑带误差的等式约束优化问题(简记为EOEP)
minΦ(x)
s.t.ci(x)=0,(i=1,2,…,m)
(1)
其中Φ,ci:Rn→R,Φ和ci是非线性的,c(x)=(c1(x),c2(x),…,cm(x))T。现在目标函数Φ∈C1及其梯度▽Φ不能直接得到,然而我们能得到Φ和▽Φ不精确(或噪声)的表达式,分别用f(x)和g(x)表示
f(x)=Φ(x)+ε(x)
(2)
g(x)=▽Φ(x)+e(x)
其中ε(x)和e(x)为目标函数和梯度的误差。
2 算法
根据经典的BFGS算法[5],借鉴无约束优化的带误差的线搜索BFGS方法[15],结合序列二次规划(SQP)方法[6],我们给出EOEP的序列二次规划-拉格朗日线搜索-BFGS方法(简称BFGS-SQP-L)如下:
步0 函数f(·)和g(·);常数0
步1
xk + 1=xk+αkdk
(3)
λk+1=Λ(xk,Bk)
步2 求搜索方向dk,即解噪声函数的二次规划子问题:
(4)
步3 求步长α*,满足Armijo-Wolfe条件
(5)
步4 如果步3这样的步长存在,令αk=α*;否则,令αk=0。
步5 如果‖αkdk‖≥ρ,则令sk=αkdk,yk=▽xl(xk+1,λk+1)-▽xl(xk,λk+1)。
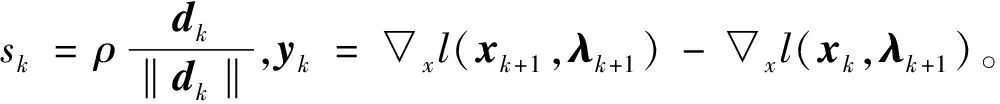
步6
(6)
其中函数Λ是λ的更新公式(见3.3节),式子中λk+1的一个常见选择是与子问题的解dk相关联的乘数,Ak=(▽c1(xk),▽c2(xk),…,▽cm(xk))。l、▽l分别是误差函数f所对应的拉格朗日函数和梯度,矩阵Bk是l在(xk,λk)处的Hessian矩阵或其近似。
3 收敛性分析
在这一节中,给出保证上述BFGS-SQP-L方法产生可接受解的条件。文中,‖·‖表示l2范数。我们的分析依赖于以下假设。
假设1 设Φ对应的拉格朗日函数L(x,λ)是有下界的且二次连续可微的,并且有M-Lipschitz连续(M>0)梯度的,即
‖▽xL(x,λ)-▽xL(y,λ)‖≤M‖x-y‖,∀x,y∈Rd
(7)
这个假设可以放宽,只要求梯度是Lipschitz连续的,取M>0简化下面定理的证明过程。
假设2 目标函数Φ和梯度值▽Φ中的误差是一致有界的,即对于所有的x∈Rd,存在非负常数εf,εg:
|f(x)-Φ(x)|=|ε(x)|≤εf
‖g(x)-▽Φ(x)‖≤‖e(x)‖≤εg
假设3 设x*是EOEP的局部最优解:
a) 存在最优拉格朗日乘子λ*使得
▽xl(x*,λ*)=▽f(x*)+▽c(x*)λ*=0
b)A(x*)=▽c(x*)列满秩;
c)B*对称正定;
d)f,ci均在λ*的某个邻域内二次连续可微,且▽2f(x),▽2ci(x)在x*的邻域内李普希兹连续。
假设2见文献[12];假设3是约束优化问题经典的标准假设,见文献[5]。以下均假定假设1,假设2和假设3成立。
3.1 Armijo-Wolfe步长的存在
Xie等[15]在应用BFGS 求解EOEP在无等式(1)约束优化问题时,给出了真实函数Φ满足的Armijo-Wolfe步长条件,同时证明了误差函数f也满足该条件。类似地,可证明在本文有约束的情况下,这样的步长也是存在的。满足等式约束条件(1)和真实目标函数Φ所对应的拉格朗日函数及梯度分别为:
▽xL(x,λ)=▽Φ(x)-▽c(x)λ=g(x)-▽c(x)λ-e(x)=▽xl(x,λ)-e(x)
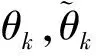


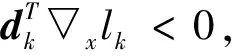
(8)
那么,存在步长αk,使得
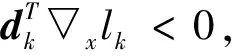
(9)
则αk满足
定理1和定理2表明,如果假设真实拉格朗日函数的梯度▽xLk不会太小,那么噪声拉格朗日函数l和梯度▽xl的Armijo-Wolfe步长存在,同时满足l的Armijo-Wolfe条件也会满足真实拉格朗日函数L。
这2个定理的证明,完全类似文献[15]定理3.4和3.5的证明过程,故略去。
3.2 延长差分参数的选择
文献[15]的定理2.1表明,运用BFGS方法处理无约束优化时,在某些假设下,对于迭代的一部分,可以建立线性收敛。特别地,要求更新中的(sk,yk)必须满足:
(10)
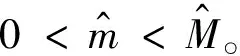
因此,在处理EOEP时,还需要作出以下附加假设。
假设4 真实拉格朗日函数L是m-强凸的,0 其中M由式(7)给出。 以下均假定假设4成立。注意,即使所给假设成立,仍然不足以支撑条件(10)成立。因此,和文献[15]一样,我们这里也采用延长差分的方法,在执行BFGS更新之前增加差分间隔并重新计算梯度,即在BFGS-SQP-L算法中 要求延长差分参数ρ满足: 以使得条件(10)成立。 为了便于研究算法的收敛性,下面我们给出子问题的解和λ乘子估计[6]。 令N(▽c(x)T)表示▽c(x)T的零空间。N(▽c(x)T)的投影矩阵记为 P(x)=I-▽c(x)[▽c(x)T▽c(x)]-1▽c(x)T 又设x*,λ*分别为(1)的一个局部最优解和相应的拉格朗日乘子,即l(x*,λ*)=0。 噪声函数的二次规划子问题 的解为 dk=hk+vk 其中 其中λk+1为拉格朗日乘子。 又由Newrton公式有 下面,分3步来研究迭代的收敛性。 1)说明BFGS-SQP-L算法搜索方向为目标函数的下降方向,即BFGS-SQP-L算法的搜索方向和真实函数的搜索方向之间成锐角。事实上,真实的二次规划子问题求解的方向 从而, 2)考虑部分好的迭代。固定标量p∈(0,1),设 (11) (12) 根据文献[15]的定理2.1,有相应的结果,证明略去。 |Jk|≥pk (13) 定理3表明,如果满足更新条件(10),当p选择接近1时,就可以认为大部分的迭代都是好的迭代。 3)可以证明,由BFGS-SQP-L算法生成的迭代的一部分产生了与其拉格朗日梯度成比例的真实拉格朗日函数的下降,以至于真实目标函数值的下降。 (14) 其中 B=max 则存在一个步长αk,满足参数(c1,c2)的(l,▽xl)的Armijo-Wolfe条件,即 且 L(xk+αkdk,λk+1)-L(xk,λk+1)≤ (15) 证明取k∈J,显然有cosθk≥β1,得 同时, L(xk+αkdk,λk+1)-L(xk,λk+1) (16) 常数A,B以及(15)中的常数不取决于目标函数或噪声,而仅取决于参数c1,c2。 本文提出了目标函数和梯度均带有界误差的等式约束优化问题(EOEP),针对该问题提出了BFGS-SQP-L算法。 受经典文献启发,我们首先给出Armijo-Wolfe线搜索条件,然后选择合适的延长差分参数,其次求解SQP子问题的搜索方向以及拉格朗日乘子迭代公式,最后给出可接受解的必要条件,使得在这些条件下,误差函数对应的拉格朗日函数的Armijo-Wolfe线搜索在目标函数对应的拉格朗日函数中产生足够的下降,以至目标函数也产生下降。由于误差总是存在的,因此我们考虑可行性仅侧重于一小部分的迭代收敛。 注意,在目标函数对应的拉格朗日的梯度比误差大得多的情况下,经典的BFGS方法尽管表现良好,但误差仍有可能破坏Hessian更新,导致拉格朗日线搜索给出带有冲突的信息。本文中的BFGS-SQP-L算法是采用拉格朗日线搜索L步长,嵌入SQP框架,对BFGS方法的简单修改,结果发现误差本身对约束的影响并不大,从而继承了没有误差时BFGS经典方法的良好性能。3.3 子问题的解和λ乘子估计
3.4 迭代的收敛

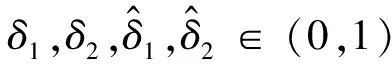
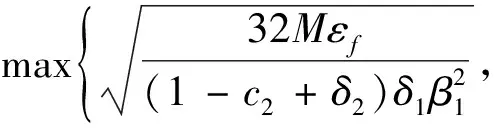
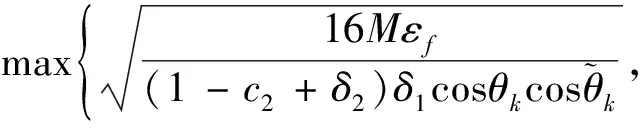

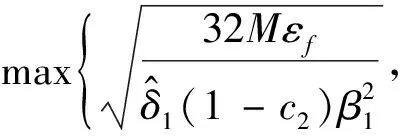

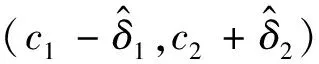
4 结束语
