基于VMI的PC构件库存管理优化研究
2022-06-10汪和平
汪和平, 刘 艳
(安徽工业大学管理科学与工程学院 安徽 马鞍山 243000)
0 引言
装配式建筑工程具有标准化设计、工业化生产、装配式施工、信息化管理及绿色化建造的特点[1],得到世界各国的一致认可。但由于装配式建筑PC构件自重大、形状固定、完整性要求较高、构件现场长时间储存困难等特性,使装配式PC构件的库存管理问题成为阻碍装配式建筑快速推广的一大难题。同时据已有数据表明,装配式建筑中建筑材料往往占工程总造价的60%~70%,其中库存费用占工程材料费用的20%~40%[2],而在装配式建筑中,PC构件是建筑材料的最主要组成部分,因此,装配式建筑PC构件库存管理问题亟待解决。
当前PC构件预制件厂为施工单位配送预制构件的周期一般在6~9天,而这种固定时间的供应计划并没有考虑到施工单位PC构件的存储与供应并不是连续的、均衡的,也没有考虑到配送次数与配送量之间的合理性。不合理的PC构件供应计划将会导致库存成本增加。因此供应商与施工单位的总库存成本最小的优化研究具有十分重要的现实意义。
随着供应链理论的深入发展,供应链思想开始应用于我国的不同行业。其中供应商管理库存(VMI)是一种新的、有代表性的供应链库存管理思想,可通过供需双方的合作,降低供应链的总库存成本。有学者通过大量的研究发现企业运用供应链管理可以节约大量的物流成本,每年节约量达到5%~15%[3],给企业带来了巨大的利润。
目前,国内外许多学者针对VMI进行了大量的研究,已将VMI应用到各个不同的领域:Dua Weraikat[4]等通过建立一个分析模型来探讨实施VMI系统对减少医院过期药品数量的影响,以提高药品供应链的可持续性。Liu Wenqian[5]等通过建立一个供应商管理的血液制品库存路径问题来优化血液制品的调度方案,结果表明该方法可有效降低血液制品供应链的运行成本。蔡建湖[6]等在季节性商品销售环境下引入VMI机制,考虑一个供应商对两个零售商的二级供应链模型,考虑供应商的最优库存决策。范旭[7]等提出为了减少供应链中不确定性的发生, 可引入CFAR、VMI机制等来加强企业应对不确定性的能力。张志韬[8]等研究基于跨境VMI供货模式下的生产-库存联合优化问题,其研究结果表明,采用供应商管理库存供货模式的库存管理是可行的。
在建筑材料库存管理研究方面,赵雪峰[9]等根据建筑企业库存管理的现状与特点,总结了建筑企业库存管理的改进方法。李忠富[10]等根据建筑企业的材料存储和供应的特性,建立动态存储模型,并证明该模型在建筑企业库存管理中的有效性。段文凤[11]等通过建立两种材料联合库存成本优化模型,求解给出恰当的订购计划,从而降低联合库存成本。黄鹏[12]等研究了单个供货商与单个建筑单位的集成情况,建立了二级供应商管理库存集成模型,说明供应商管理库存模式能够降低供应商和建筑单位的总库存成本。许杰峰[13]等提出了基于BIM的建筑供应链管理,利用IT机制来保证供应链目标实现。邵必林[14]等提出了利用建筑供应链管理方法控制成本并建立模型,并与传统模式下的库存成本进行比较,结果证明应用该方法库存成本能有效减少。以上文献对建筑业库存管理的研究证明库存管理优化能有效降低建筑业的库存管理成本,但在这些研究中大多仅以施工单位为视角,考虑如何合理安排订购策略从而减少库存以及库存成本,几乎没有研究是从供应商的角度出发去考虑如何去降低建筑供应链的总库存成本。
本文在VMI条件下,针对预制件厂和施工单位的库存管理问题,建立单个预制件厂多个施工单位的二级供应链库存成本模型,并采用改进灰狼算法对模型进行求解,将求解结果与传统配送方案结果比较,验证基于VMI模式下库存管理的优越性。
1 问题描述与模型建立
1.1 VMI集成与运行
VMI模式改变了原来预制件厂与施工单位各自为政的库存管理模式,强调双方的库存集成及合作,供应商和施工单位将构件需求计划、工程进度计划及PC构件的运输、消耗等信息进行共享,从而促进供应链库存管理的持续改进,进而共同制定构件库存计划,其具体流程图如图1所示。
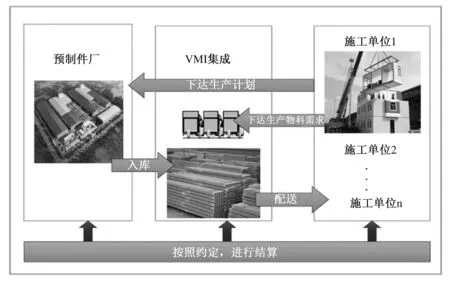
图1 VMI集成流程图
在实践中,一个预制件厂存在多个订单,同时可为多家施工单位进行供货,因此将一家预制件厂与多个施工单位进行集成,其集成结构如图2所示。

图2 供应商管理库存集成图
1.2 问题描述
某一装配式PC构件预制件厂可同时为多个施工单位供应多种类型PC构件,预制构件供应商拥有对PC构件的库存管理权,并且能保证预制构件充足。每个施工单位都有至少一种或多种构件需求,且需求量确定,在施工单位施工过程中,装配式PC构件从到货到全部消耗完成需要一定的时间,因此施工单位也存在库存。本文基于供应商管理库存对供应链之间存在的库存成本进行讨论,并将现实供应链简化为构件供应商与施工单位两个环节来讨论,建立一个构件供应商对多个施工单位的二级供应链库存成本模型,研究当一个构件供应商面对多个施工单位未来T期的需求,供应商如何安排供应计划使得VMI二级供应链库存成本最小。
1.3 问题假设
为完成模型的设定,本文在如下假设的情况下进行讨论:(1)当供应商的PC构件到达工地后,施工单位能够立即投入施工。(2)配送车辆每辆车的装载量相同且已知预制构件加工厂可供调配的车辆有限。(3)PC构件的运输车辆由预制构件厂车队自行提供,不考虑第三方物流。(4)不考虑车辆运输时间与装卸货时间。(5)VMI集成环节仅考虑构件供应商与施工单位。(6)各施工单位的工程进度可完全控制,即各施工单位的构件需求量依据可控的进度,可在计划工期内所需构件数量和所需时间完全确定。(7)不允许缺货。
1.4 符号和决策变量
本文对所建模型的符号定义如下:i为施工单位编号,i=1,2,3…,N;N为施工单位数量;j为配送车辆编号,j=1,2,3…,M;M为可供调配的车辆数目;k为派往施工单位i的车次编号,k=1,2,3,…,Ki;Ki为为施工单位i进行配送的车次数量总和;r0为单位车辆启动成本;r为单位可变运输成本;e0i为供应商到施工单位i的距离(0代表供应商);A0为供应商固定备货成本;Ai为施工单位固定订货成本;ni为施工单位i的订货次数;h0为供应商单位时间单位构件数库存成本;hi为施工单位i处单位时间单位构件数库存成本;xij为车辆j运往施工单位i的构件数量;Tip为施工单位i处第p次供货时间;Tni为供应商第ni次供货时间;di为施工单位i的需求量;W为车辆装载容量;αf为工地i所需构件的单件重量,f=1,2,3,…,F;f为构件种类;Zijk表示施工单位i的第k次服务是否由车辆j提供。
2 模型建立
2.1 施工单位库存成本
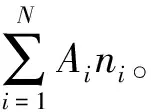
2.2 供应商库存成本
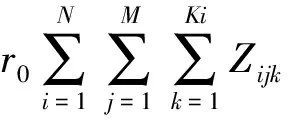
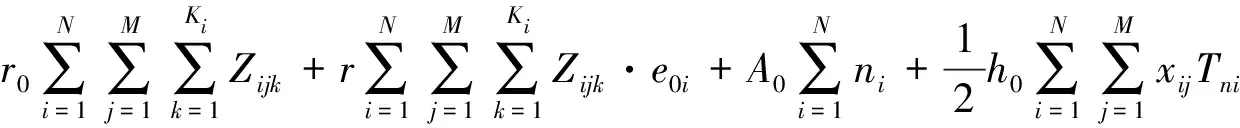
2.3 VMI下的库存成本模型
基于以上的问题描述及假设,建立在VMI条件下的库存总成本C最小的目标函数
minC
=min(C1+C2)
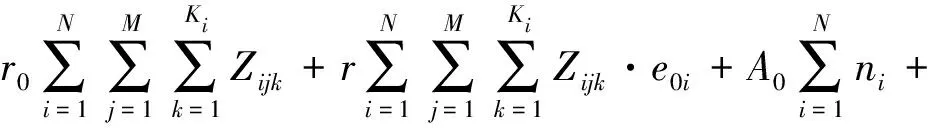
约束条件如下所示。
(1)时间限制条件
Ti(p-1)≤Tip≤Tni
(1)
(2)缺货限制条件,保证在计划工期内各个施工单位的装配式PC构件充足,不允许缺货
(2)
(3)车辆荷载量约束条件,运输的车辆不能超负荷作业
(3)
(4)单次车次约束条件,每个施工单位每个车次的构件由一辆车实施配送
(4)
(5)总车次约束条件:预制构件厂所有配送车辆的配送次数总和与全部施工单位需求的配送车次总和必须是相同的
(5)
(6)非负约束条件,在模型中配送量及需求量均为非负值
xij≥0,di≥0
(6)
3 模型求解算法设计
本文采用灰狼优化算法求解该模型。灰狼优化算法具有结构简单、需调节的参数少等特点,因此在对问题的收敛速度和求解精度方面都有良好的性能。灰狼优化算法基本原理可参考文献[15]。
为了提高搜索结果的求解精度以及收敛速度,本文采用自适应调整步长公式对算法进行改进。同时为了解决灰狼优化算法在攻击猎物阶段容易陷入局部最优的问题,引入模拟退火算法,使得灰狼优化算法跳出当前局部最优,并最终趋于全局最优。
3.1 编码方式及初始种群的生成
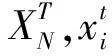
式中:i为施工单位,t为时间节点(i≤N,t≤T)。
3.2 自适应调整步长
群智能算法中步长的规定将影响搜索结果的精度,所以本文将采用文献[16]的方法,根据α狼的位置自适应调整的步长。当灰狼距离α狼位置较远时,将以较大步长进行搜索;当灰狼距离α狼位置较近时,将以较小步长逼近α狼,以加快收敛速度,步长公式为
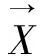
3.3 适应度函数
适应度函数的选取直接影响到算法是否能找到最优解以及其收敛速度,而适应度函数大多是根据目标函数确定的。在本文中,目标函数为供应商管理库存下的最小库存成本,则采用目标函数(最小库存成本)的倒数作为适应度函数。F越小,适应度值越大,则适应度函数为
3.4 结合模拟退火算法
模拟退火算法(SA)在退火过程中不但接收好的解,还以一定的概率接收差的解,能够避免在搜索过程中陷入局部最优。因此在灰狼算法中,若搜索结果陷入局部最优,则在迭代过程中以一定的概率随机选取一部分狼群进入模拟退火过程,以避免算法陷入局部最优。
具体结合方式如下: 当狼群中的每一匹灰狼都完成一次搜索之后,能得到一个此次搜索的最优解,然后在此次最优解之外随机生成其他解集,最后由模拟退火算法来判定是否接受新解以代替之前的最优解。
3.5 算法流程图
改进灰狼优化算法流程图如图3所示。
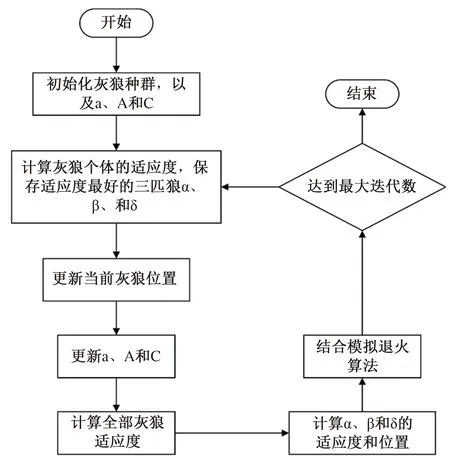
图3 算法流程图
4 案例应用
4.1 算例构造
现有一装配式PC构件供应商,同时为3家施工单位进行供货,该构件供应商主要生产4种装配式构件(预制楼梯、预制阳台板、预制外墙和预制叠合板),且施工的各阶段构件需求量已知。单位车辆固定成本为198元,单位车辆变动成本为3.47元/km,供应商单次补货成本为1200元,施工单位单次订货成本均为600元,施工单位库存持有成本为8.4元/(天·块),供应商库存持有成本为3.5元/(天·块),车辆荷载为25 t,可供调配的车辆为6辆,构件供应商到施工单位1、2、3的距离分别为21 km、65 km、35 km。其各类构件的单件重量见表1,各施工单位的需求量、需求时间见表2。
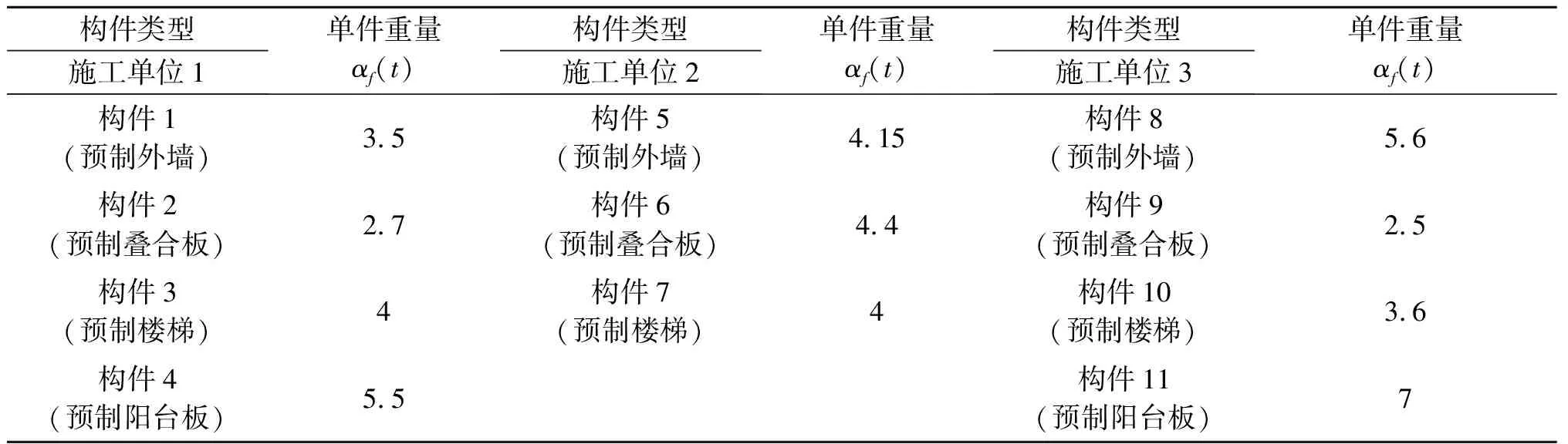
表1 各类构件的单件重量

表2 各施工单位的构件需求量
4.2 算例结果分析
将案例中的数据代入到总库存成本模型中,采用Matlab2019a编程实现,并分别用经典遗传算法、基本灰狼算法、改进灰狼算法进行求解,各算法分别运行500次,3种算法的目标函数值值与迭代次数变化关系曲线如图4所示。
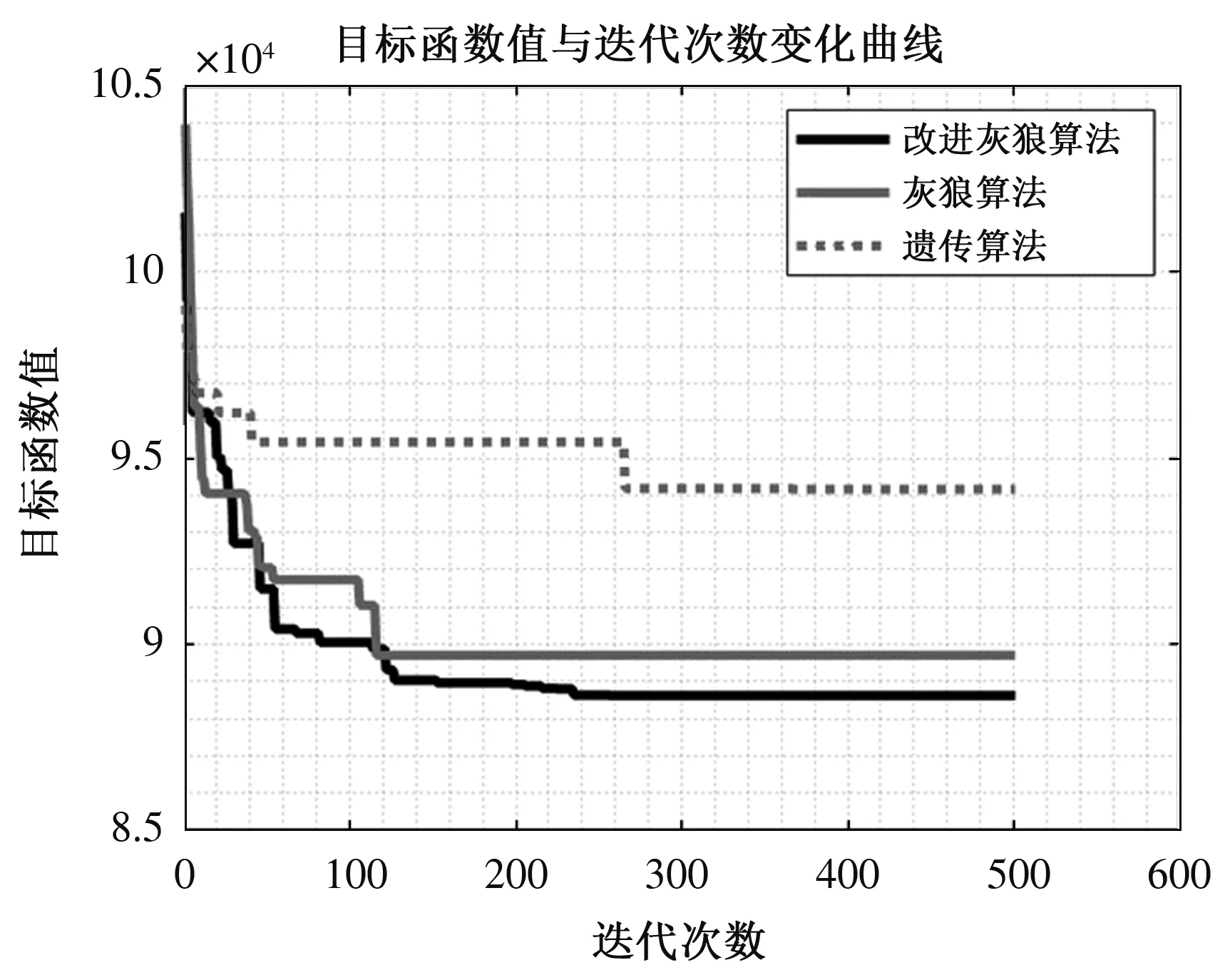
图4 3种算法迭代过程对比图
在VMI模式下根据二级供应链库存成本模型求得的最优库存成本为88577.17元,最优供货方案及成本详见表3。

表3 运用VMI模型求解的最优运输方案及成本
为验证模型的有效性,将模型求解得到的最优供货方案与成本,与传统周期性供货方案结果进行比较。传统周期性配送方案及成本如表4所示,各个算法与传统配送方案最终成本对比见表5。

表4 传统周期性配送方案及成本

表5 成本对比
根据以上案例结果和成本对比可以看出,基于VMI下的装配式PC构件库存管理的方法可有效减少预制件厂与施工单位双方的库存成本,可证明该方法在降低库存成本方面有明显的优势。
通过对比图4中3种算法的收敛情况可知,改进灰狼算法比遗传算法和灰狼算法更具有优越性。遗传算法与灰狼算法收敛速度快,但都具有陷入局部最优的缺陷,在采用了模拟退火和自适应调节步长的情况下,改进的灰狼优化算法能够快速地跳出局部最优,并得到更好的结果。也证明改进后的灰狼优化算法性能及结果更为优越。
5 小结
本文基于一个PC构件供应商对多个施工单位的库存管理问题,分析了供应商管理库存环境下的上游预制件厂与下游施工单位之间存在的库存成本,建立了二级供应链库存成本模型,并根据实际案例,应用改进灰狼优化算法对模型进行求解,验证模型的有效性。研究结果表明,在装配式建筑库存管理问题中采用VMI模式是可行的,通过与传统的周期性配送方案对比发现,采用VMI模式不仅满足了原有需求,还使得整个供应链的库存总成本更低,更具有经济优越性;同时通过对3种算法的对比分析,验证了改进灰狼算法的优越性。
