基于V-REP的主动柔顺式机器人轴孔装配仿真
2022-06-10刘尚争朱清慧刘群坡
刘尚争, 朱清慧, 刘群坡
(1.南阳理工学院智能制造学院 河南 南阳 473004;2.河南理工大学电气工程与自动化学院 河南 焦作 454000)
0 引言
装配在机械制造工业中占有较大比重[1],随着工业机器人的广泛应用,利用机器人进行轴孔装配的场景越来越多,然而在轴孔装配作业的过程中出现的卡阻现象会对装配工件甚至机器人造成损害[2]。为解决轴孔自动装配中的卡阻问题,确保装配过程顺利进行,提出一种主动柔顺装配的方法进行去卡阻,使轴孔装配作业可以平稳顺利地进行。
在主动柔顺装配方面,国内学者李焕[3]提出基于阻抗控制的机械臂末端工具的柔顺控制,以腕力传感器反馈值为依据进行相应调整,将其控制在一定范围内,对精细操作具有指导意义。再有学者王小涛[4]设计出一种空间五指灵巧手单指力柔顺控制系统,在对接过程中采用阻抗控制方法进行接触力和位置控制,可快速跟踪手指关节位置以及精确控制腱张力的大小。
本文针对6自由度机器人轴孔装配过程中经常遇到的卡阻问题,设计了一种主动柔顺装配方法。为模拟机器人在实际的轴孔装配中遇到的卡阻现象,在V-REP(virtual robot experimentation platform)仿真平台下搭建仿真环境并进行了实验验证,证明了该主动柔顺装配策略理论上的正确性与可行性[5-7]。
本文主要研究内容包括:对机器人正逆运动学的分析、轴孔装配理论分析、主动柔顺装配控制系统的设计以及基于V-REP的主动柔顺装配仿真[8,9]。
1 轴孔装配系统模型建立
1.1 仿真装配平台
如图1所示,轴孔装配的系统主要由UR5机器人、六维力传感器、待装配工件和工件孔组成。为简化仿真,在装配平台中未添加夹具,将工件直接连接在六维力传感器上。
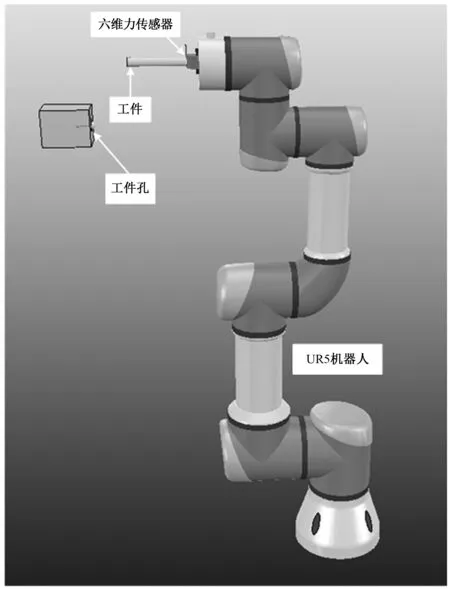
图1 V-REP仿真装配平台
1.2 UR5机器人运动学分析
1.2.1 机器人D-H建模
机器人的每个连杆都可以用4个运动学参数来描述,两个参数用于描述连杆本身,两个参数用于描述连杆之间的关系,这种用连杆参数描述机构运动关系的规则称为D-H(Denavit-Hartenberg)方法[10]。并有给出连杆参数定义如下:ai为沿着Xi轴,从Zi轴移动至Zi+1轴的距离;αi为围绕Xi轴,从Zi轴旋转至Zi+1轴的角度;di为沿着Zi轴,从Xi-1轴移动至Xi轴的距离;θi为围绕Zi轴,从Xi-1轴旋转至Xi轴的角度。据此,建立如图2所示的UR5机器臂的连杆坐标系。

图2 UR5机械臂连杆坐标系
根据图2机械臂各连杆坐标的相对位置,可得到UR5机械臂的D-H参数表如表1所示。
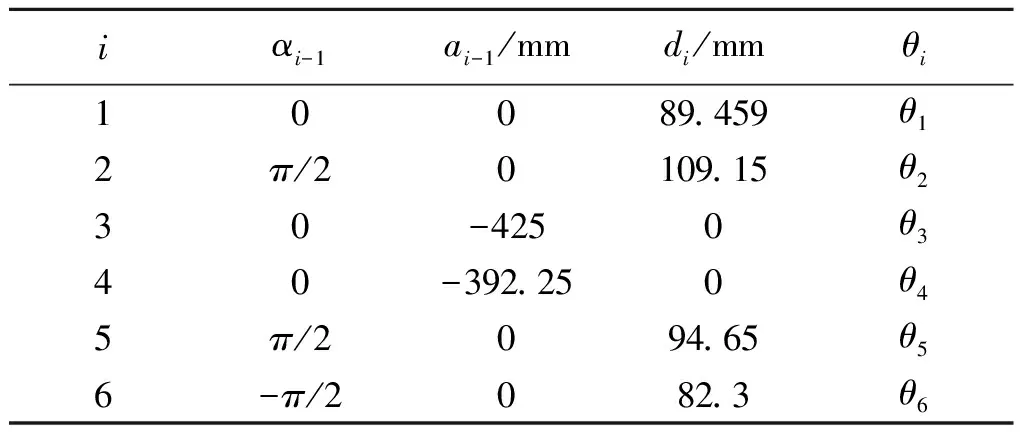
表1 UR5机械臂D-H参数表
1.2.2 机器人正运动学分析
在已知机械臂当前各关节角值的情况下,则可通过对机械臂正运动学的分析得到机械臂末端工具的位置和姿态。下面对机械臂末端坐标系{6}到固定坐标系{0}的变换矩阵进行推导[11,12]。
rot(xi,ai)·trans(xi,αi)
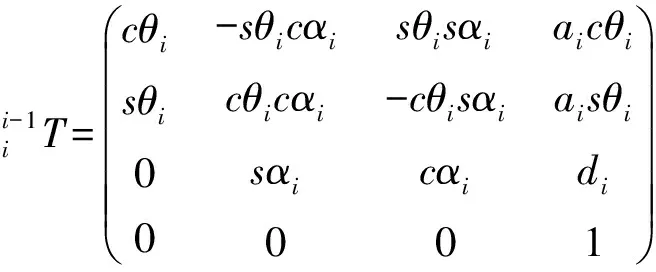
代入UR5机械臂DH参数表中各参数可得到各连杆变换矩阵
故腕部坐标系{6}相对于坐标系{0}的变换矩阵为
(1)
1.2.3 机器人逆运动学分析

θ2=atan2(s2,c2)
θ3=±arccos(m2+n2-a22-a32/2a2a3)
θ4=atan2(t1,t2)-θ2-θ3
θ5=±arccos(axs1-ayc1)
θ6=atan2(m/s5,n/s5)
其中
m=d6ay-py;n=axd6-px;
m2+n2-d42≥0;axs1-ayc1≤1;
s2=(a3c3+a2)n-a3s3m/a22+a32+2a2a3c3;
c2=m+a3s2s3/a3c3+a2;
s5≠0;m2+n2≤(a2+a3)2;
t1=-s6(nxc1+nys1)-c6(oxc1+oys1);
t2=ozc6+nzs6;
2 轴孔装配原理分析
2.1 工件装配条件分析
轴孔装配过程共有两步,寻孔阶段和入孔之后的姿态调整阶段。理想情况下的工件入孔情况如图3所示,工件与轴孔既没有位置偏差也没有姿态偏差,工件中心轴线与轴孔中心轴线完全重合,在整个装配过程中,工件与轴孔之间没有接触力或接触力在一个合理的范围内,则不需调整姿态。

图3 理想情况下工件入孔示意图
在现实操作环境中,由于机器人的精度误差、测量误差等,装配过程中会出现工件中心轴线与轴孔中心轴线不完全重合的情况。若工件中心轴线与轴孔中心轴线偏差角较小(如图4和图5所示),在整个装配过程中,机械臂无需调整姿态仍可顺利入孔。但当该偏差角达到某一特定值时,若不调整工件姿态,在装配过程中会产生卡阻,工件将无法顺利入孔,并会对工件产生一定的磨损,严重时会损坏机械臂。

图4 恰能入孔的极限情况

图5 恰能无卡阻入孔的建模分析
设轴孔深度AB为h,工件直径CE为d,轴孔直径BE为Q,工件中心轴线与轴孔中心轴线所形成的倾斜角为θ。
由几何关系可知
BD=h·tanθ
DE=d·cosθ
由BD+DE=BE可知
h·tanθ+d·cosθ=Q
(2)
在实际装配环境中,轴孔深度、工件直径及轴孔直径均为已知条件,代入公式中即可求得工件恰能无卡阻入孔的最大偏差角θ。

图6 工件不能入孔临界情况
图6为工件不能入孔的临界情况,可以看到工件的一侧底角已经入孔,而另一侧底角还卡在轴孔边缘,此时工件与轴孔轴线的夹角为α,对该夹角进行计算,由图中的几何关系可知
(3)
当工件与轴孔轴线的偏差角大于α时,工件不能入孔,此时机械臂需要重新定位轴孔入口处圆心的位置,并通过旋转工件减小工件与轴孔轴线的偏差角,使工件可以顺利入孔。
2.2 工件与轴孔各接触状态分析
在轴孔装配过程中,经常遇到的情况是图7中(a)和(b)两种情况,其中图(a)为一点式卡阻的情形,图(b)为两点式卡阻的情形,此时必须要调整工件姿态才能保证装配过程顺利进行,使工件顺时针或逆时针旋转,尽量使工件中心轴线与轴孔中心轴线重合,有两种可能情况。
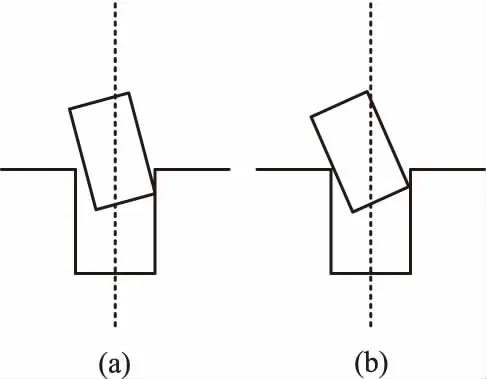
图7 常见的轴孔装配卡阻现象
1) 旋转机械臂末端夹具
由图8可知,只旋转机械臂末端夹具的方案是行不通的,调整后工件左侧会与轴孔内壁发生碰撞,进而损坏工件或机械臂。
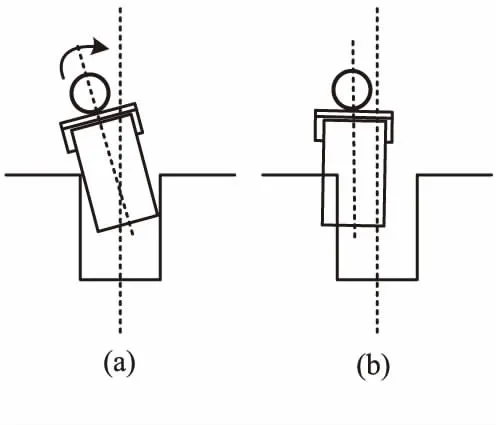
图8 仅旋转机械臂末端夹具
2)以工件自身某一点为旋转中心进行旋转
由图9中可以看出,绕工件自身m点进行旋转后,工件不会与轴孔内壁发生碰撞,并且可以实现工件中心轴线与轴孔中心轴线重合。调整前后机械臂末端夹具的姿态与位置均发生了变化。
2.3 卡阻姿态分析
2.3.1 一点式卡阻
如图10所示,装配过程中出现的一点式卡阻现象,也是在装配过程中最容易出现的卡阻情况,工件在轴孔内任意的卡阻现象都可以分解到力传感器坐标系的XOY和XOZ两个平面,如图11所示XOY坐标系的力分解,XOZ平面类似。
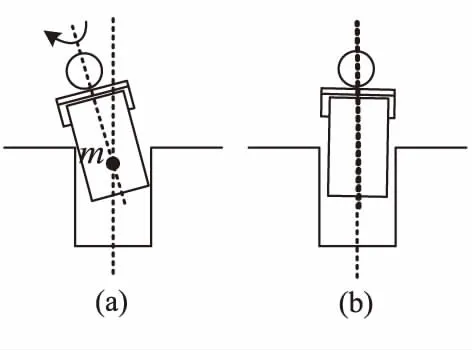
图9 以工件的m点为中心进行旋转
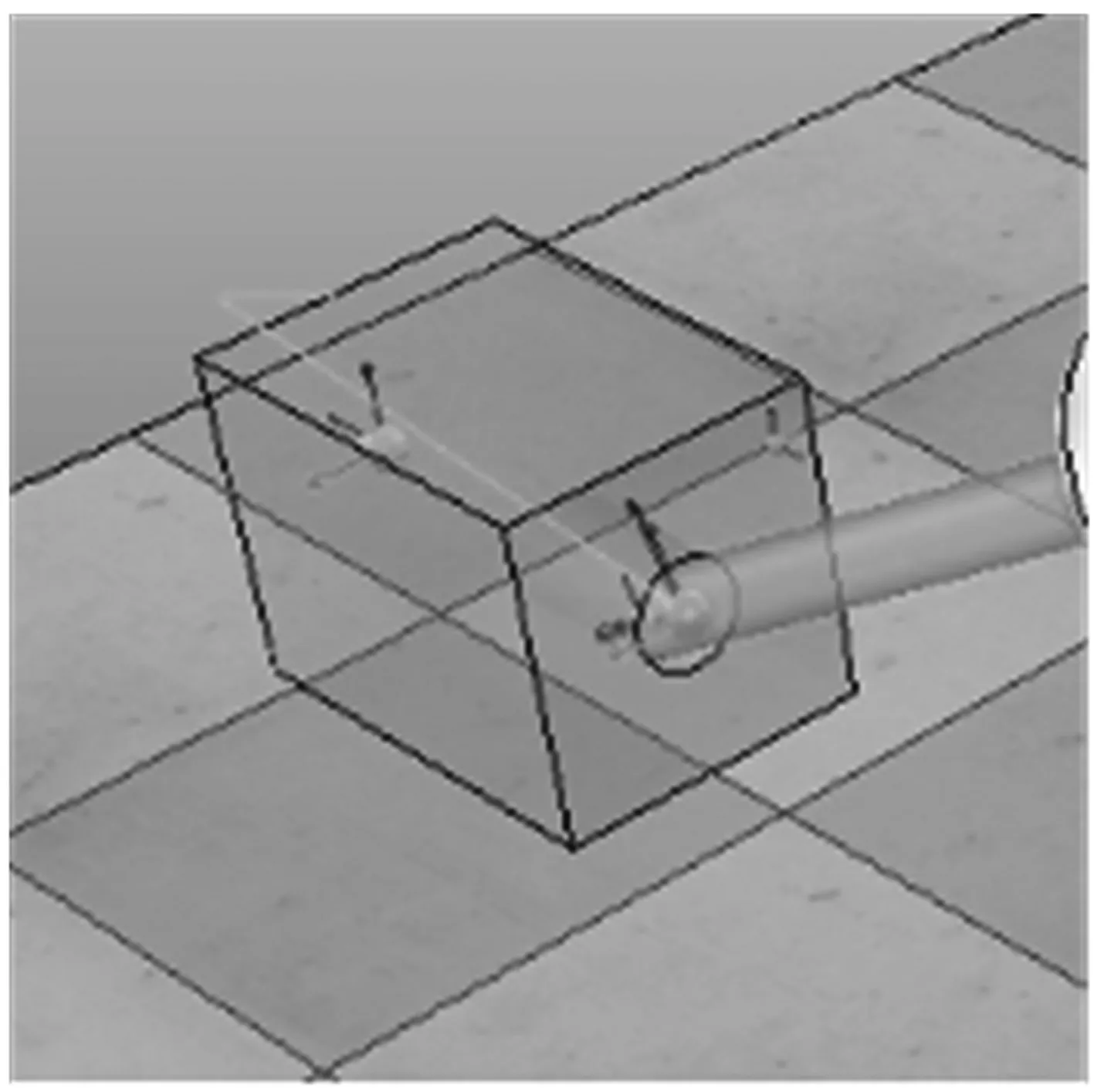
图10 轴孔装配卡阻图
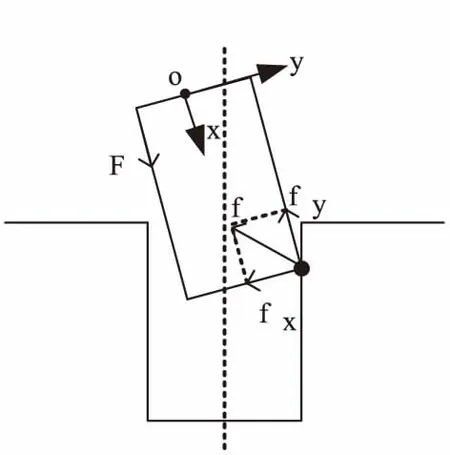
图11 在XOY平面的卡阻现象
2.3.2 两点式卡阻
当工件装配形成如图12所示的两点式卡阻时,轴孔对工件的反作用力F2必然大于F1。此时类似一点式卡阻现象,可将工件旋转后再尽行装配,最终会变为如图11所示的一点式卡阻现象。由此可以看出,两点式卡阻现象是一点式卡阻现象的特殊情况,仍可按照一点式卡阻情况进行分析。
3 主动柔顺装配系统设计
3.1 卡阻建模分析
3.1.1 自适应姿态调整中心点建模
三维空间轴孔装配过程中发生卡阻现象时的一个场景如图12所示。对该卡阻现象进行建模分析,如图13所示。其中A、C两点分别为工件中心轴线与其上下底面的交点,B、E两点所在直线为轴孔中心轴线,M点为工件中心轴线与轴孔中心轴线的交点,力传感器坐标系与工具坐标系姿态相同。

图12 两点式卡阻

图13 工件卡阻现象的平面建模分析
以世界坐标系为参考坐标系,已知A点坐标为(Xa,Ya,Za),E点坐标为(Xe,Ye,Ze),C点坐标为(Xc,Yc,Zc),工件长度AC=L,AB为A点到轴孔中心轴线的垂线距离,DC为C点到轴孔中心轴线的垂线距离。
根据上图可推导出B点坐标为(Xa,Ye,Ze),D点坐标为(Xc,Ye,Ze)
则根据以上点坐标可推导出
BD=Xa-Xc
由几何关系可知,△ABM相似于△CDM,故可得到如下关系式
AB/DC=BM/MD=SM/MC=k1
BM+MD=BD
得
BM=(k1/1+k1)(Xa-Xc)
(4)
AM=L(k1/1+k1)
(5)
M点在参考坐标系下坐标为
(Xa-(k1/1+k1)(Xa-Xc),Ye,Ze)
其中
3.1.2 工具坐标系与目标坐标系各轴夹角计算
图14为工件卡阻现象的空间建模分析,其中AM所在直线为工件中心轴线,BM所在直线为轴孔中心轴线,A′M为AM在A′BMM′平面上的投影,A″M为AM在A″BM平面上的投影。工具坐标系{0}与目标坐标系{7}均位于M点,若要工件中心轴线与轴孔中心轴线完全重合,则需要将旋转中心M点坐标系{7}的姿态调整到与目标坐标系{0}的姿态完全一致。

图14 工件卡阻现象的空间建模分析
设工具坐标系与目标坐标系的Z轴夹角为β角,由图14可以看出
β=∠AMA″
在直角△AA″M中
sinβ=AA″/AM
进而得
β=arcsin(|Za-Ze|·L·(1+k1)/k1)
设工具坐标系与目标坐标系的Y轴夹角为α角,由图14可以看出
α=∠AMA′
在直角△AA′M中,
sinα=AA′/AM
进而得
α=arcsin(|Ya-Ye|·L·(1+k1)/k1)
(6)
3.2 基于动态自适应M点的运动学分析
工件入孔出现卡阻情况时,应调整机械臂使工件分别绕着旋转中心M点的Y轴和Z轴旋转一定角度。因此需要根据工件旋转中心M点的期望位置和当前姿态信息,通过逆运动学解析出机械臂调整后的各关节角度大小。
设工具坐标系位于M点处,坐标系{6}与旋转点M之间的关系如图15所示。机械臂关节6到工件上底面圆心点A点的距离可测,设该距离已知为d,则坐标系{6}与工件上旋转中心点 M点的距离为
d7=d+AM

图15 坐标系{6}与工具坐标系{7}之间的关系
由公式5得
d7=d+L(k1/1+k1)
其中L为工件长度。
则由变换矩阵定义可知,位于M点的坐标系{7}相对于坐标系{6}的变换矩阵
(7)
3.2.2 M点坐标系旋转前后的变换矩阵
工件旋转前后,M点的位置不变,仅姿态发生了变化,设M点旋转前的坐标系为{7},旋转后的坐标系为{7 ′}。若力矩值My>0,工件应绕旋转中心点M的Y轴逆时针旋转ε角,则坐标系为{7 ′}由坐标系{7}绕自身Y轴旋转-ε角得到,则变换矩阵为
(8)
若力矩值My<0,工件应绕旋转中心点M的Y轴顺时针旋转ε角,则坐标系为{7 ′}即为坐标系{7}绕自身Y轴旋转ε角,则变换矩阵为
(9)
ε角有两种选择方案:(1)ε角每次选定为某一固定角;(2)ε每次以工具坐标系与目标坐标系的Z轴夹角β角为参考标准进行取值
ε=kβ=k·arcsin(|Za-Ze|·L·(1+k1)/k1)
(10)
若力矩值Mz>0,工件应绕旋转中心点M的Z轴顺时针旋转η角,则坐标系{7 ′}即为坐标系{7}绕自身Y轴旋转η角,则变换矩阵为
(11)
若力矩值Mz<0,工件应绕旋转中心点M的Z轴逆时针旋转η角,则坐标系{7 ′}即为坐标系{7}绕自身Y轴旋转-η角,则变换矩阵为
(12)
η角有两种选择方案:(1)η角每次选定为某一固定角;(2)η每次以工具坐标系与目标坐标系的Y轴夹角α角为参考标准进行取值
η=kα=k·arcsin(|Ya-Ye|·L·(1+k1)/k1)
(13)
如图16所示,工件旋转前机械臂末端连杆坐标系及M点坐标系分别为{6}和{7},旋转后机械臂末端连杆坐标系及M点坐标系分别为{6′}和{7′}。根据机械臂正运动学分析可知

图16 工件旋转前后机械臂末端连杆坐标系{6}及M点坐标系{7}的变换
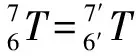
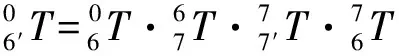
由此即可计算出机械臂调整后的坐标系{6′}到坐标系{0}之间的变换矩阵为
(14)
根据机械臂逆运动学解析公式即可求出机械臂调整后的各关节角度。
当力矩反馈值My小于0时,工件应绕旋转中心点M的Y轴顺时针旋转ε角。假设当前机械臂各关节角分别为θ1、θ2、θ3、θ4、θ5、θ6,机械臂关节6到工件上底面圆心点的距离为d,工件长度为L,则根据公式(14)可得
由逆运动学解析公式即可求出机械臂调整后的各关节角度。其中:s234表示sin(θ2+θ3+θ4),c234表示cos(θ2+θ3+θ4),其余以此类推。
3.3 基于力反馈的自适应装配流程
在装配过程中,实时获取机械臂末端的六维力传感器各个方向的力矩值。正常装配过程中,六维力传感器的3个方向的力矩值会有一个最大值,则设置力矩阈值稍大于正常装配过程的最大力矩值,若3个方向的力矩值均不超过该阈值,则工件继续沿着轴孔前进;若力矩值超过阈值,证明此时出现了卡阻现象,则转去执行去卡阻方案[13,14]。
卡阻现象发生时,首先计算出工具旋转中心M点,然后判断Y轴力矩是否超限,若超限则继续判断力矩的方向。若力矩大于零则应使工件绕M点Y轴处顺时针旋转一定角度,若力矩小于零则应使工件绕M点Y轴处逆时针旋转一定角度。接下来判断Z轴力矩是否超限,超限则使工件在M点处沿自身坐标系Z轴旋转一定角度,旋转方向也由力矩的正负决定。若力矩为正则逆时针旋转,反之则顺时针旋转。此时读取传感器的力矩反馈值,若已成功消除卡阻则工件继续执行入孔作业,否则继续调整至无卡阻状态再进行装配。通过将工件与轴孔接触时六维力传感器的力矩反馈值控制在一个合理的范围内,就可以保证机械臂平稳顺利地完成装配任务,装配流程如图17所示。其中调整角度的计算以工件当前工具坐标系与目标坐标系之间的偏差角为参考标准来动态调整工件旋转角度。当偏差角较大时使工件以一个较大的角度旋转,从而减少调节次数。当偏差角较小时就适当减小工件旋转角度,从而避免出现超调现象。

图17 装配流程图
4 实验仿真
在仿真中首先设定起始工作环境,使在装配过程中出现卡阻,如图18所示设定工件入孔夹角为30°时。
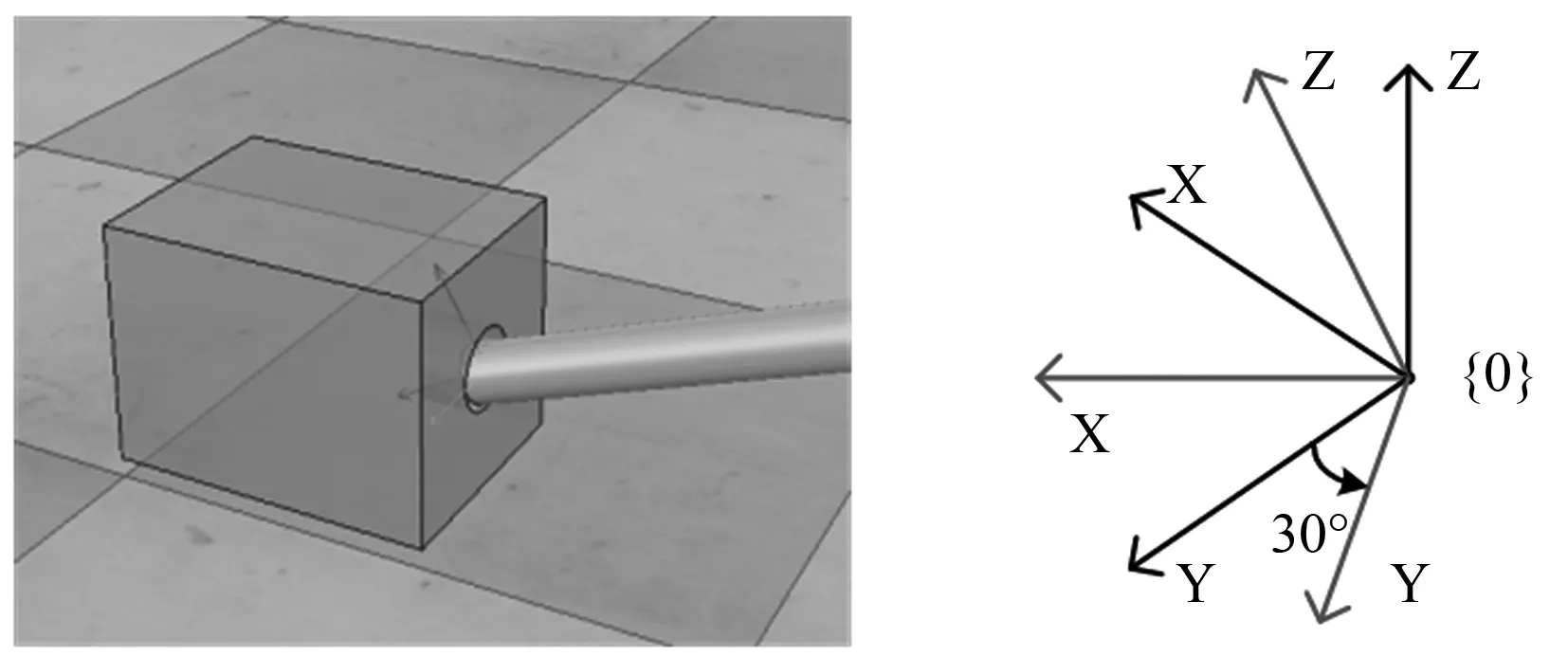
图18 工件入孔起始偏差角
机械臂根据力传感器反馈力矩值大小自适应调节装配过程,如图19所示,在装配过程中,机械臂调整两次即可令工件与轴孔中心轴线重合。由图20所示的机器人各个关节角值易可看出两次调整平滑且流畅。最终实现了工件的装配如图21所示。

图19 力传感器X、Y、Z方向受力变化

图20 各关节角度变化
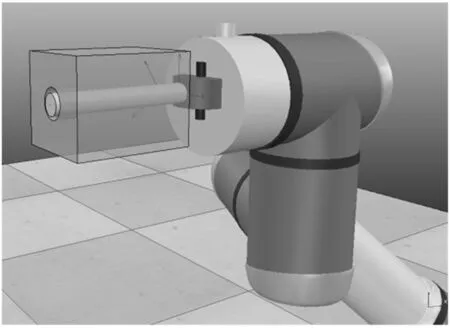
图21 装配完成
由仿真可以看出,该主动柔顺式装配方案在装配过程中机械臂的调节次数较少,缩短了机器人的轴孔装配时间,且装配过程柔顺。
