基于震源机制的套管变形量控制方法研究*

吴建忠，乔智国，慈建发，何 龙，连 威，李 军,4

(1.中国石化西南油气分公司科技管理部 四川 德阳 618400；2.中国石化西南油气分公司石油工程技术研究院 四川 德阳 618400；3.中国石油大学(北京)克拉玛依校区 新疆 克拉玛依 834000；4.中国石油大学(北京) 北京 102249)

0 引 言

中国川渝盆地页岩气开发过程中套管变形现象显著，截至2019年10月，长宁区块压裂211口井，其中49口井出现套管变形，比例为23.2%。套管变形导致压裂成本增加，井筒寿命降低，气体产量下降，亟待解决。针对此现象，科研工作者针对套管变形的机理和控制方法进行了大量分析。田中兰等[1]基于页岩气井工程实际，分析了热应力、弯曲应力、轴向应力等对套管应力的影响；Sugden等[2]综合井眼轨迹、温度变化以及储层应力的影响，明确了套管承受的热应力和弯曲应力；蒋可等[3]分析了水泥环性能、居中情况、缺失情况等对套管载荷的影响，认为高强度、低刚度、居中良好的水泥环有利于降低套管应力；刘奎等[4]建立了局部载荷作用下套管载荷计算模型，认为增加壁厚、减小外径有利于减小套管变形；席岩[5]等基于热传导理论，建立了体积压裂过程中套管温度和热应力计算模型，明确了动态温度影响下的套管抗拉、抗外挤强度变化规律，认为热应力能使套管抗拉强度降低23%，内压和热应力耦合能使套管抗外挤强度降低19%；Furui[6]认为套管在内压交替变化和轴向屈曲共同作用下存在变形的风险；杨尚谕等[7]从套管自身强度出发，认为高钢级、低径厚比的套管有利于提高套管的极限承载能力，同时，复合管串设计能够有效降低套管使用成本。

随着MIT多臂井径测井、微地震、蚂蚁属性体成像以及斯通利波测井等手段在页岩气井中的应用，科研工作者对井下套管变形形态、变形位置与地层物性参数、断层、天然裂缝发育情况的相关性有了进一步认识，并在此基础上对套管变形的原因有了进一步分析。Chipper-field[8]、Hossain[9]和Wu等[10]认为复杂网络的形成会使套管承受剪切、滑移载荷，从而导致套管失效；Lian等[11]基于岩石损伤理论和微地震分布特征，认为套管变形的原因是压裂后地层压实与错动；Zoback[12]、Qian[13]等认为裂缝非对称扩展使储层产生剪应力，这种剪应力使地层滑移并剪切套管；沈新普等[14]发现套管变形和微地震信号的非均匀分布存在对应关系，并建立了数值计算模型分析了压裂压力和套管变形量之间的关系；陈朝伟等[15-17]基于现场施工实际明确了压裂液激活断层的路径，并基于震源机制方法以及套管变形量反演了断层半径和滑移量。在此基础上，席岩[18]、郭雪利等[19]采用震源机制方法对页岩气井套管变形机理进行了进一步分析，量化了水泥环、套管等参数对套管变形量的影响。

水力压裂过程中，无论是形成人造缝网还是断层滑移，都涉及地层岩石的拉伸或剪切破坏，岩石破坏产生的能量释放以微地震事件的形式展现，这些微地震事件产生的地震波信号可以在一定范围内被检波器检测到，基于记录到的微地震信号结合对应的解释方法可以得到震源信息。微地震信号强度不同，意味着地层产生的拉伸/剪切量不同。因此，通过监测微地震信号的强度，可以确定断层大小和滑动量的相关信息，为监测或控制套管变形提供了一种有效的方法。

1 基于震源机制的断层滑移量分析

1.1 震源参数基本关系

水力压裂过程中，地层在压裂液作用下产生裂缝，岩石变形过程中能量的释放可以通过微地震进行监测，和天然地震的数学定律类似，微地震解释中也存在基于震源参数的数学计算模型。其中，地震矩是量化地震整体大小的量度，与地层断裂破坏过程密切相关。其定义为式(1)[20]：

M0=GAD

(1)

式中：M0为地震矩，N·m；G为剪切模量，Pa；A为断层平均滑移量，m；D表示断层面积，m2。

矩震级Mw是利用地震矩的大小确定的震级，是描述地震力学强度的物理量。矩震级和地震矩关系如式(2)[21]：

(2)

矩震级可通过地震波谱的综合反演求得，综合式(1)和式(2)可知，量化断层平均滑移量的前提是明确活化断层的面积。

Stein等[22]基于圆形断层滑移情况提出了滑移半径的计算方法，主要是使用断层面上的应力降进行分析。所谓应力降，指的是断层累积的应变突然释放后产生应力的变化，断层滑移半径r0计算方法如式(3)：

(3)

式中：Δσ为地震能量释放时的应力降，Pa。

联立式(1)、(2)、(3)可以明确圆形断层半径和断层滑移量的表达式为：

(4)

(5)

从式(5)可以看出，断层滑移距离、断层半径以及矩震级均与应力降相关，Mukuhira 等[23]对压裂过程中的微地震数据进行了统计分析，结果如图1所示。可以看出，压裂过程中产生的应力降集中在0.01～1 MPa区间，极少超过1 MPa。

图1 地震矩和断层面积的关系[23]

压裂过程中断层滑移的主要控制因素为断层内的孔隙压力，压裂液进入断层则是孔隙压力变化的直接原因。压裂液进入地层后使地层孔隙压力增加，对应的增量为式(6)～式(8)：

(6)

(7)

(8)

式中：λ为拉梅系数，Pa；G为剪切模量，Pa；ΔV为压裂液体积，m3；V为饱和岩石体积，m3；μ为泊松比，无因次；E为弹性模量，Pa。

断层稳定性一般使用摩尔库伦准则进行判定，依据如式(9)：

τ=τ0+η(σn-P)

(9)

式中：τ为作用在断层面上的剪应力，Pa；τ0为内聚力，Pa；η为摩擦系数，无因次；σn为正应力，Pa，P为孔隙压力，Pa。

设断层面内孔隙压力增加至P′时断层活化，同时设ΔP=P′-P，则对应的摩尔库伦准则为式(10)：

τ′=τ0+η(σn-P′)

(10)

联立式(9)和式(10)可得式(11)：

(11)

压裂过程中每一个微地震信号对应一次岩石的破坏过程，而每一次岩石的破坏又存在对应的应力矩，Kostrov等[24]明确了岩石应变和应力矩之间的关系式(12)：

(12)

式中：Δεij应变张量，无因次；Mij为应力矩张量，N·m。

作用在断层面上的剪应力发生变化时，由弹性本构方程可知式(13)：

Δτ=GΔε

(13)

联立式(12)和式(13)，可得式(14)：

(14)

进一步联立式(6)和式(14)，可得式(15)：

(15)

根据古登堡-里克特复发关系式，一定区域足够长的时段内，不同震级大小的地震数量遵循的关系式如式(16)：

(16)

式中：N表示地震震级大于M0的总数，次；A，B为和地震相关系数，无因次。

设微地震事件过程中产生的最大地震矩为M0(max)，式16转变为式(17)[25]：

(17)

一级压裂过程中所有微地震事件产生地震矩的总和为不同地震矩对应次数的积分：

(18)

联立式(15)和式(18)可得式(19)：

(19)

上述公式推导过程为计算断层半径和滑移量提供了依据。首先，对于页岩地层中的断层而言，其拉梅常数和剪切模量为固定值，参数B的取值范围一般为0.5～1，断层面内摩擦系数一般为0.6～1，断层滑移产生的地震矩可以通过矩震级进行计算，而矩震级可以通过现场仪器测量，如陈朝伟等[20]测量现场矩震级最大值为3.5，因此，通过式(19)可以估算含断层页岩区域压裂液的体积；然后，基于现场微地震信号三维分布规律，明确压裂液波及页岩的体积，结合式(6)可以分析地层孔隙压力的变化值；再次，根据式(11)可以明确压裂前后断层内的应力降；最后，根据式(4)和式(5)可以计算断层半径以及滑移量。

综上所述，通过监测或者控制矩震级的大小，可以明确压裂过程中断层滑移量。由于断层滑移是导致套管变形的直接因素，套管变形到一定程度(变形量大于套管内径与桥塞直径之差)时导致桥塞无法正常通过，因此可以通过控制矩震级的大小达到控制套管变形的目的。

1.2 断层滑移量计算

以长宁H9-1井为例，基于微地震信号监测结果结合地层参数对断层滑移量进行预测。基本参数为：井深4 560 m，垂深2 571 m, 水平段长 1 400 m，第18段压裂过程中桥塞在第21段(井深3 338 m)位置遇卡，导致第19、20、21段压裂施工放弃，H9平台裂缝预测结果和套管变形情况如图2所示。

图2 H9平台裂缝预测结果和套管变形情况

该井压裂过程中使用微地震手段监测人造缝网的扩展情况，考虑到3 338 m位置处的套管变形主要由第18段压裂施工导致，因此本节着重分析第18段压裂过程中的微地震信号分布特点，结果如图3所示。

图3 H9-1井微地震信号分布

从图3中可以看出，H9-1井第18段压裂过程中受图2中天然裂缝影响显著，除在18段附近地层形成缝网(俯视图区域(1))外，大部分压裂液沿着天然裂缝形成的通道进入断层附近地层(俯视图区域(2))，高压压裂液进入断层后使断层面内孔隙压力升高，达到临界时断层活化导致套管变形。

根据现场微地震测量可知,断层区域最大矩震级为3.4级，而正常裂缝扩展过程对应的矩震级小于0。取式(19)中B值为0.5与1之间的均值0.75，断层面摩擦系数η为0.6，测井结果显示，页岩弹性模量为34.2 GPa，泊松比为0.17，可以计算图3俯视图中进入区域(2)压裂液的体积为1 525 m3。

进一步结合微地震信号估算压裂液波及页岩地层体积，将含断层区域的微地震信号简化为立方体，如图3中立体侧视图所示，立方体尺寸为549 m×426 m×98 m，根据式(6)可以计算含断层区域孔隙压力增加量为1.149 MPa，进一步根据式(11)可计算断层面内的应力降为0.69 MPa，结合图1可知此值在合理范围内。最后结合式(4)、式(5)可以计算断层半径和滑移量分别为123.7 m和42 mm。

设压裂过程中监测到的最大矩震级在1～3.4级之间变化，保持地层以及压裂参数不变，分析最大地震矩变化对地层滑移量的影响，结果如图4所示。

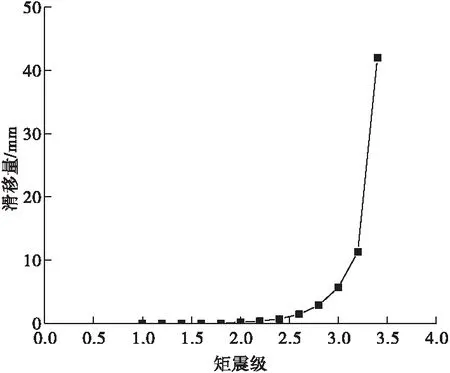
图4 矩震级与断层滑移量对应关系

从图4中可以看出，当矩震级小于2级时，地层滑移距离接近0，随着地层滑移距离的进一步增加，地层滑移距离和矩震级呈指数关系。

考虑到不同井深、不同区域页岩弹性模量存在一定区别，同时，压裂液进入断层后，压裂液在断层面之间产生浮水效应和润滑效应使断层面内的摩擦系数降低,因此有必要分析页岩弹性模量和断层面内摩擦系数对地层滑移量的影响，在H9-1井微地震测量的基础上，进一步分析地层弹性模量和断层面内摩擦系数对地层滑移距离的影响，计算结果如图5、图6所示。

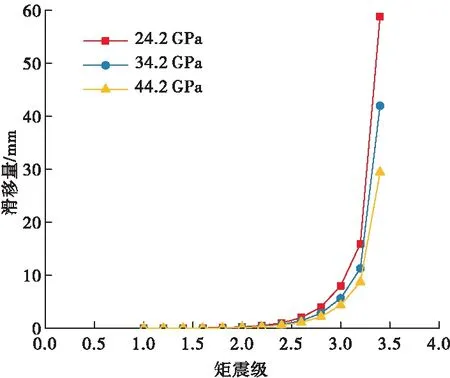
图5 弹性模量影响

图6 摩擦系数影响结果

从图5中可以看出，地层弹性模量对滑移距离具有一定影响，具体体现为当矩震级高于2.5级时，弹性模量越低，滑移距离越大；但是当矩震级小于2.5级时，不同弹性模量条件下地层滑移量基本相同。对于断层界面摩擦系数而言，断层面摩擦系数越小，滑移距离越大，当矩震级小于2.5时，不同摩擦系数条件下地层滑移量也基本相同。

前文以H9-1井为例，分析了压裂过程中可人为监测的矩震级与地层滑移距离之间的关系。现有研究结果认为，地层滑移是导致套管变形的主要原因，但是地层滑移量和套管变形量之间的关系尚未明确。因此，有必要建立有限元模型分析地层滑移量和套管变形之间的关系，从而明确矩震级和套管变形量的关系，最终明确施工过程中允许的最大矩震级。

2 地层滑移条件下套管变形量分析

2.1 地层滑移数值模型建立

按照H9-1井的井筒尺寸和地层参数计算地层滑移条件下的套管变形量。地层、水泥环设置为线弹性材料，套管设置为理想弹塑性材料，可承载应力峰值为屈服强度，随后进入塑性变形状态。套管-水泥环-地层组合体的几何以及力学参数见表1。

表1 组合体几何与力学参数

根据圣维南原理，模型尺寸取大于5倍井眼尺寸，模型长、宽、高分别为7、1.3、1.3 m。地层以滑移面为分界，右侧地层相对左侧地层产生相对位移错动，从而模拟地层滑移，地层滑移数值计算模型如图7所示。

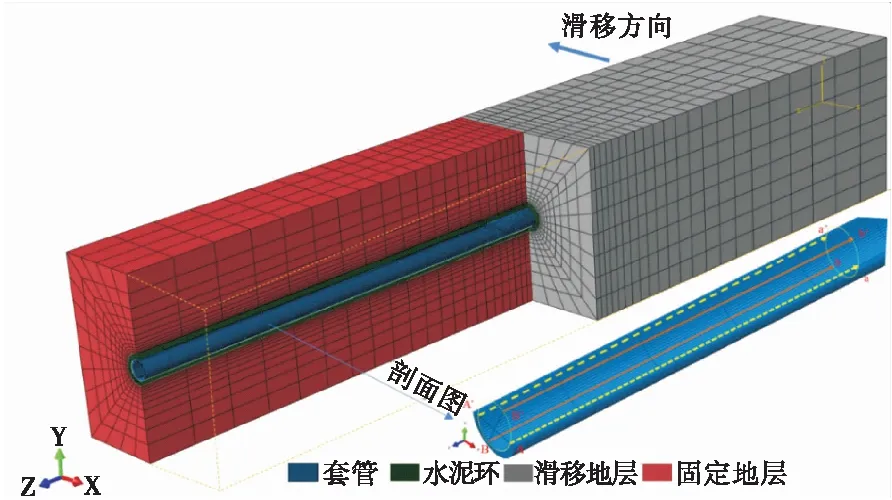
图7 地层滑移数值计算模型

2.2 参数设置及网格划分

在载荷设置方面，设置套管内压等于静液柱压力与地面泵压之和，模型中取110.7 MPa；同时在页岩地层上施加初始地应力，其中，水平最大、最小和垂向地应力分别为75、64和82 MPa。

在网格划分方面，地层、水泥环以及套管均采用六面体网格，地层、水泥环和套管采用变密度网格划分形式，并在接近断层位置进行网格细化，用以准确分析套管的变形规律。

在接触设置方面，由于不考虑固井胶结面的脱粘行为，将套管外壁和水泥环内壁、水泥环外壁和地层井眼之间的接触属性设置为绑定。断层界面之间的摩擦属性设置为摩尔-库伦摩擦，摩擦系数为0.6。

在边界条件设置方面，对固定地层进行位移约束，对滑动地层施加固定位移，代表沿断层面发生的相对错动，其值取微地震信号反演的地层滑移量，大小为42 mm。

2.3 套管变形结果分析

图8为地层滑移后套管位移与塑性变形量数值有限元计算结果。从图8可见，地层滑移条件下套管存在明显的剪切变形，地层滑移量为42 mm时，套管变形量为13 mm。同时可以分析套管内径发生变化的机理为：地层滑移时，套管仅在180°圆周上承受剪应力，导致一侧产生显著的塑性变形，而另一侧基本处于弹性变形状态，从而使内径产生变化。

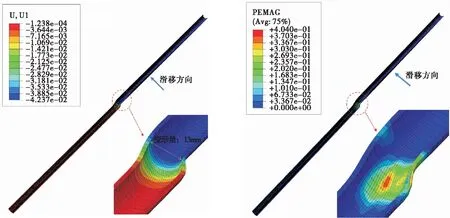
图8 套管位移与塑性变形

进一步分析套管在不同方向上的变形情况，将套管在轴向上分为Aaa′A′和Bbb′B′两个方向，如图9所示，分析套管在上述两个方向上内径的变化规律。

如图9即为A′a′Aa和B′b′bB方向上套管内径变化规律，显然，A′a′Aa方向上的套管变形量明显大于B′b′bB方向上的套管变形量，原因在于地层的剪切载荷主要作用在A′a′Aa曲面形成的圆周上，B′b′bB曲面形成的圆周基本上不承载地层滑移产生的剪切载荷。

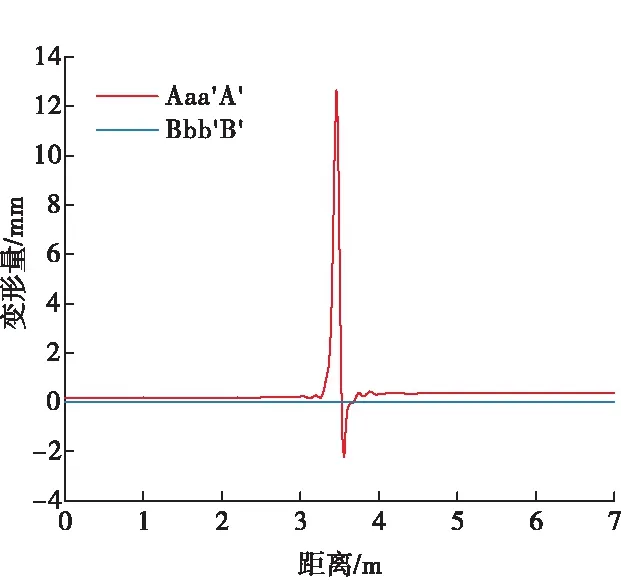
图9 套管变形计算结果

进一步分析变形量与滑移量之间的对应关系，结果如图10所示。可以看出，套管变形量随地层滑移量的增加基本上呈线性增加，当地层滑移量为42 mm时，对应的套管变形量为13 mm。对比现场多臂井径测量数据可知套管变形量为15.2 mm，测量值和计算值较为接近，说明了数值计算结果的正确性。

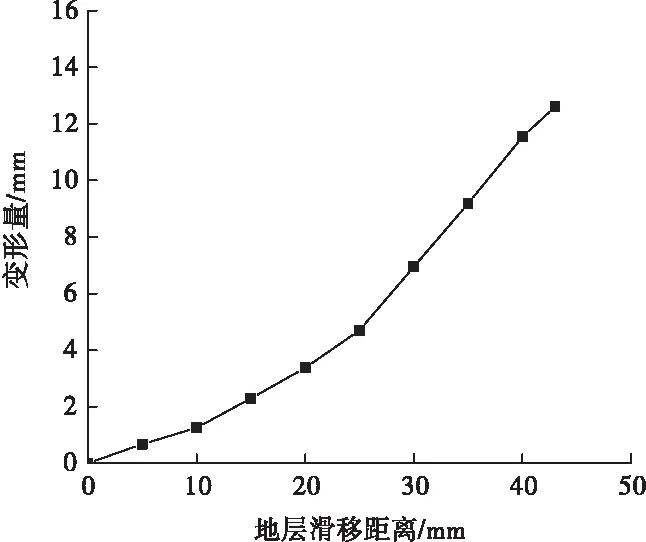
图10 地层滑移量和套管变形量的关系

2.4 套管变形影响因素分析

套管通过水泥环和地层胶结在一起，地层滑移产生的剪切载荷通过水泥环传递至套管外壁，因此套管产生的剪切变形不仅受地层滑移量的影响，也受套管自身几何、力学参数的影响。因此有必要分析上述参数对套管变形量的影响。

2.4.1 套管壁厚

套管壁厚对于套管强度影响显著，增加壁厚有利于缓解套管应力和增加套管强度，保持其它参数不变，设置壁厚在10.7～16.7 mm之间变化，分析不同壁厚条件下的套管变形量，结果如图11所示。可以看出，增加套管壁厚对于缓解套管变形量具有一定效果，但并不显著，壁厚由10.7 mm增加至16.7 mm时，变形量由15.03 mm降低至10.73 mm，降低幅度为28.6%，但变形量为10.73 mm时并不能保证桥塞顺利通过。因此，增加套管壁厚对于保护套管具有一定效果，但不能完全避免套管变形。

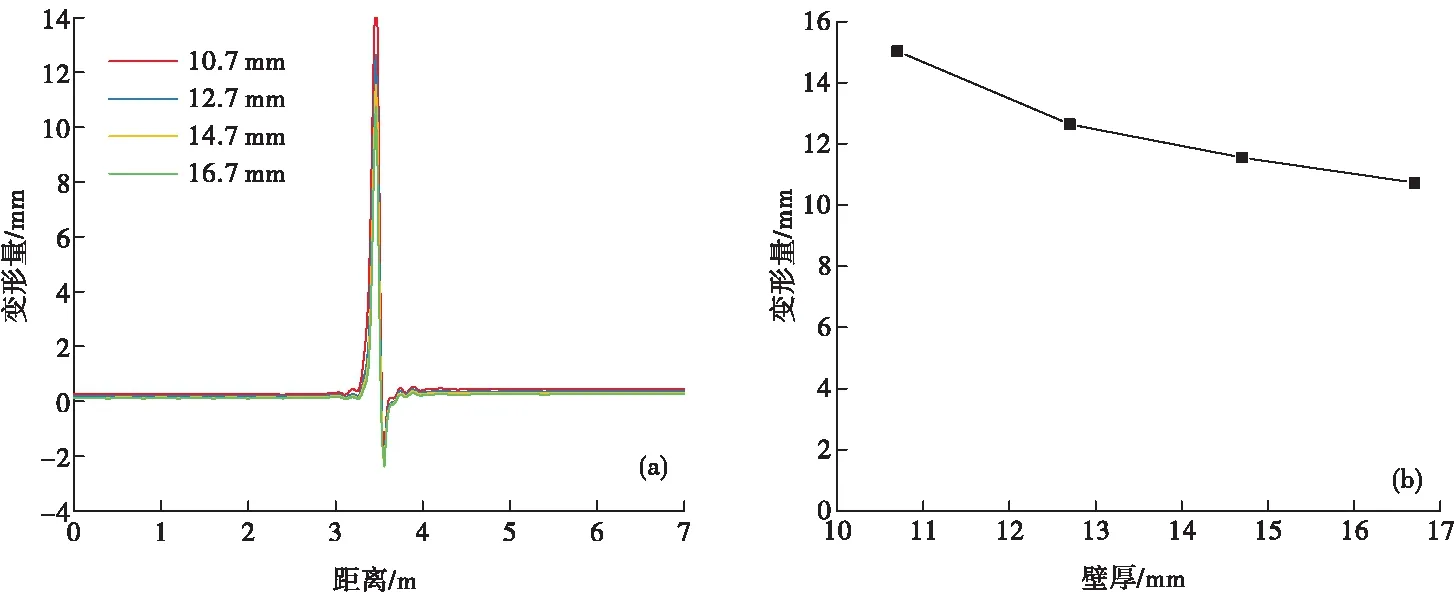
图11 不同套管壁厚下套管变形量

2.4.2 套管屈服强度

受套管材料以及锻造工艺的影响，不同钢级套管的屈服强度存在显著区别。从材料力学的角度来看，材料弹性模量一定的条件下，屈服强度越高，弹性变形区间越大，抵抗外载荷的能力越强，越有利于其完整性。保持其它参数不变，设置套管屈服强度在600 MPa至1 200 MPa的过程中，分析屈服强度对套管变形量的影响，如图12所示。

图12 套管屈服强度对套管变形量影响

从图12中可以看出，套管屈服强度对于缓解套管变形具有一定的效果，屈服强度由600 MPa增加至1 200 MPa的过程中，套管内径变化量由15.43 mm降低至10.01 mm，降低幅度为35.1%，变形量降低至10.01 mm时同样不能保证桥塞完全通过。因此，与增加套管壁厚效果类似，提高套管屈服强度对于缓解套管变形具有一定效果，但不能完全避免套管变形。

3 套管变形量与矩震级对应性分析

前述分析明确了地层滑移条件下不同影响因素对套管变形量的影响，结果对比如图13所示。可以看出，套管壁厚和屈服强度对于缓解套管变形具有一定影响，地层滑移量是套管变形的主要影响因素。

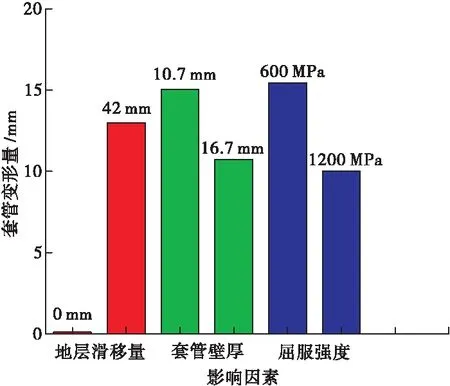
图13 套管变形影响因素

图4明确了地层滑移量和矩震级的关系，图10明确了套管变形量和地层滑移量之间的关系。忽略套管壁厚、屈服强度对套管变形量的影响时，可以进一步明确套管变形量和矩震级之间的对应关系，如图14所示。

图14 矩震级和套管变形的关系

从图14可以看出，当矩震级在0～3级范围内时，套管变形量基本为0。随着矩震级进一步增加，套管变形量基本上呈指数增加，此时桥塞存在遇阻的风险。因此，多级压裂过程中若监测到矩震级接近3级时，应该降低施工强度甚至停止施工作业，从而降低套管变形的风险。

4 结论

本文基于套管剪切变形机理，分析了多级压裂过程中防止地层滑移导致套管变形的方法。主要得到以下结论：

1)基于震源机制基本方程，结合地层滑移的摩尔-库伦准则，推导了矩震级与地层滑移量的关系。研究结果表明：矩震级小于2级时，地层滑移量基本为0，矩震级大于2级时，地层滑移量随着矩震级的增加呈指数增加。

2)结合所计算的地层滑移量，建立了地层滑移条件下的套管变形量计算模型，计算结果表明：套管变形量的主要影响因素为地层滑移距离，二者基本呈线性关系；壁厚由10.7 mm增加至16.7 mm时，屈服强度由600 MPa增加至1 200 MPa、套管变形量分别降低28.6%、35.1%，提高屈服强度和壁厚具有一定效果，但不能完全避免套管变形。

3)套管变形量和矩震级的拟合结果表明，矩震级小于3级时，套管变形量基本为0，矩震级大于3级时，套管变形量随着矩震级的增加呈指数增加，建议多级压裂过程中检测到矩震级接近3级时，降低施工强度或者停止施工，防止地层滑移导致套管变形。