一种新型电容式六维力/力矩传感器设计及解耦分析

姚起宏，王奉阳，黄 伟，2，蒲明辉，2

（1.广西大学机械工程学院，广西 南宁 530004；2.广西大学 广西制造系统与先进制造技术重点实验室，广西 南宁 530004）

0 引言

六维力/力矩传感器能够实现空间直角坐标系中3个方向力分量FX、FY、FZ和3个方向的力矩分量MX、MY、MZ的测量，其作为实现工业智能化重要的设备之一，广泛应用在机械加工、汽车制造、智能化机器人、航空航天等领域[1，2]。力传感器种类较多，目前国内外已经有较成熟的六维力/力矩传感器。按力信号转换方式可分为应变式、压电式、压磁式、光学式电容式等[3，4]，其中应变式力传感器是目前研究最多、应用最为广泛的一种力传感器[5-6]。应变式力传感器灵敏度高、响应快，但其结构和电路设计都很复杂，力矩解耦困难。在测量时需要额外的A/D转化器，才能完成。其应变片对粘贴精度要求高且容易损坏，对电磁噪声过于灵敏[7]；电容式力传感器具有结构简单、灵敏度高、动态性能好、能实现非接触式检测等优点。同时，目前国内电容式六维力/力矩传感器的研究相对较少，故对电容式传感器进行深入研究有一定的实际意义。

传统的电容传感器可分为3类：极距变化型、面积变化型和介质变化型[8]。但由于边缘效应的存在，会出现非线性误差。随着电容边缘效应的研究不断深入，基于电容边缘效应原理的传感器的实现将成为可能。

本研究基于平行极板变极距电容原理和电容边缘效应原理，采用一种新型的双十字差动式结构，通过极板对于不同分量的力的差动关系，对六维力/力矩传感器的测量进行解耦。并通过仿真实验验证了该传感器的解耦特性，为后续的物理实验奠定了一定的基础。

1 电容式六维力/力矩传感器原理分析

1.1 平行板变极距式电容传感器

当忽略电容边缘效应时，平行极板间电容量C的计算式为：

式中ε=ε0·εr为介电常数；ε0为真空介电常数；εr为极板间介质的相对介电常数；S为两极板的相对有效面积；d为两极板间距。

变极距平板电容传感器的结构原理图如1。

图中，上极板为静电极，下极板为动电极，d0为两极板初始间距，当动电极移动了△d，电容量变换了△C，初始电容为C0。电容相对变化量为：

当△d/d0＜＜1时，由泰勒公式得其理想拟合方程：

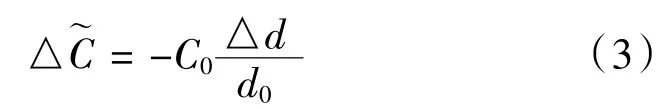
其理论线性度δL：

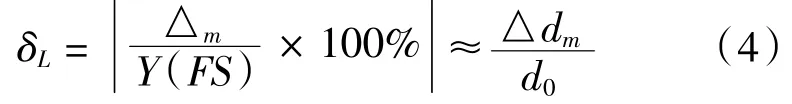
式中△m为最大拟合偏差，Y（FS）为传感器的满量程输出。

由式（2）～（4）可知，变极距型平板电容传感器△C与△d理论上为非线性关系，当极距变化很小时可近似为线性关系，故其常用于小位移变化的测量中[9]。

由式（3）可得变极距型平板电容传感器的灵敏度Kd为:

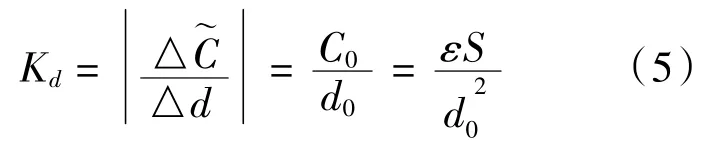
由式（5）可知变极距平行极板电容传感器的灵敏度和极板面积正相关，和极板间距成负相关。

1.2 垂直板变极距式电容传感器

动极板和静极板采用垂直布置的形式，如图2所示，静极板非常薄，仅0.1μm，两极板间距h，静极板宽度为W，高度为H。当在两极板间施加电压时，两极板将形成一个边缘场[10，11]。两极板产生的边缘电容为[12]：

图2 电容边缘效应垂直式结构

当极板间距变化△h时，初始电容C0改变△C：

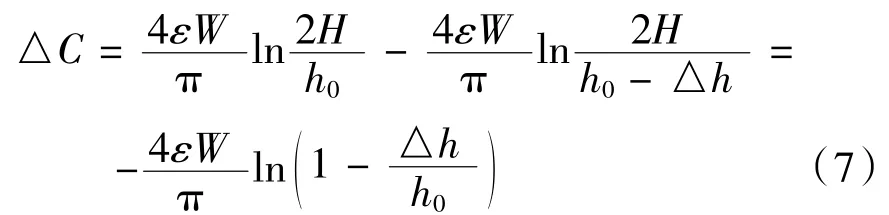
将式（7）进行泰勒展开得：

当动极板位移量远小于极板初始间距时，即△h远小于h0时，忽略式（8）中高阶项，得：

则最大拟合偏差Δmax：

将最大变形量Δhmax和最小变形量0代入式（9）可得基于垂直极板的电容式力传感器满量程输出Y（FS）为：

理论线性度为：

对比式（4）和（12）可得，基于电容边缘效应的变极距垂直型电容传感器的输入输出特性为非线性，但其线性度相对平行板线性度提高了一倍。

根据式（9）可得灵敏度Kvert：

式中h0为两极板初始间隙。

根据式（13）可知，变极距垂直型电容传感器的灵敏度Kvert与静极板的宽度W正相关，与两极板初始间隙h0负相关，与静极板高度H无关。

若设平行极板的面积S=W H，极板间距d0=h0，则由式（5）可得变极距平行板电容传感器的灵敏度为：

比较（13）和（14）两式可知，电容边缘效应变极距垂直型电容传感器的灵敏度Kvert相比Kd在仅考虑极板间距的情况下受到极板间距的影响更小，即其灵敏度更稳定。

2 传感器结构设计

该传感器主要应用于协作机器人末端关节力的测量，根据应用场景，传感器的量程见表1。

表1 传感器量程

传感器结构图如图3，整体结构如图3所设计传感器结构图如图3，整体结构如图3（a），下层S型弹性梁起到X、Y方向分力的解耦作用，并能提高传感器的灵敏度，考虑到加工可行性，将本传感器进行分层，如图3（b）。传感器工作时，外圈固定，内圈受力带动测量层产生位移，通过PCB电路板检测由此引起的电容量的变化。

图3 传感器结构图

3 测量及解耦分析

传感器的信号传递过程见图4，前而已对位移和电容之间关系进行了详细分析，这里测量及解耦验证时仅考虑力-位移之间的关系。

图4 信号传递图

测量结构平面见图5，采取双十字结构布置电容器极板。图5中的虚线为电容器静电极，静电极布置在PCB板（在图7中未显示）的下底面上，其厚度方向（垂直X Y平面方向）的尺寸很小，在5μm～105μm范围，这是由PCB板覆铜工艺所决定的。其中C1～C4为垂直极板布置方式，原理示意图见图2，C5～C8为平行极板布置方式，原理示意图如图1，采取了上文描述的两种电容测量原理实现六维空间力/力矩的测量。

图1 变极距型电容传感器原理图

图5 测量体平面结构

各维力测量原理 切向力FX通过垂直电极板测量（FY同理），如图6（b）所示，受到X方向力后，垂直布置的电极板极距发生变化，从而引起电容量变化，通过检测电容量的变化达到测量目的。Z方向的力矩M Z通过C1和C2，C3和C4之间的差动关系进行测量，如图6（c）。

图6 Fx、Fy和Mz的测量原理

法向力FZ和力矩MX、MY移引起电容的变化见图7。FZ作用时，所有平行极板电容器极矩变小电容增大（图7（b））。当受到MX时（MY同理），如图7（c），两侧平行布置的极板，一侧间距增大，另一侧减小，通过这种差动式关系来进行MX的测量。

图7 法向力和力矩的测量原理

表2列出了每个电容器受到各正向力/力矩时电容变化的趋势。在表中，“⇑”和“⇓”代表相对强劲的电容的增加和减少，“↑”、“↓”分别表示相对较弱的增加和减少。“～”意味着电容几乎没有改变。

表2 电容随相应力的变化趋势

由表2可知，每个电容器在6种不同的力分量输入下变化趋势不同。此处分析仅考虑位移和力的关系，假设输入力与位移变化呈线性关系，可以建立此传感器的位移和力之间的测量方程为:

其 中F= [Fx，Fy，Fz，Mx，My，Mz]T，△h=[△h1，△h2，△h3，△h4，△h5，△h6，△h7，△h8]T，T为6×8的标定矩阵。

4 解耦可行性的仿真验证

对传感器结构建立有限元模型如图8。

图8 传感器机械结构有限元模型

对外圈施加固定约束，内圈通过rbe3单元进行加载。由于有限元分析材料为弹性材料，在应力小于材料屈服强度时位移和力的关系是线性的，仿真分析时仅对力各分量满量程单次加载，对C1～C8电容所产生的有效测量位移进行提取（均取动极板节点位移的平均值），并根据式（15）计算标定矩阵T。

进一步任取3组力进行仿真，提取测量位移数据，对解耦矩阵进行验证，数据表见表3。

表3 解耦误差分析

通过式（15）计算所得的力和实际施加的力进行对比发现，仿真解耦计算结果和实际施加力之间误差不超过0.9%，可见误差较小解耦效果较好，故仿真验证初步满足解耦要求。

5 结束语

（1）本研究设计的六维力/力矩传感器的测量原理，采用基于电容边缘效应和平行板变极距电容原理进行测量，理论分析表明其整体线性度比仅采用平行板电容传感器要好，同时垂直和平行两种极板的结构布置方案能更好地利用空间，使所设计的传感器结构更加紧凑。

（2）测量体采用双十字式结构，通过不同极板之间的差动关系进行解耦，测量原理简单；并通过仿真验证了解耦的可行性，为后续静态物理标定试验打下了一定的基础。