基于FPGA的星地量子信号同步方案
2022-06-10王潮泽李凤芝刘尉悦
李 叶,金 标,王潮泽,李凤芝,刘尉悦
(宁波大学信息科学与工程学院,浙江 宁波 315211)
0 引言
量子密钥分发(QKD)基于量子不确定性原理和未知量子态不可克隆等量子力学基本原理,以量子态为信息载体,在相距遥远的用户间建立相同的随机数序列,实现安全的密钥共享[1-4],广泛应用于地面光纤链路、地面自由空间链路和星地自由空间链路[5-8]。时间同步作为一种量子信号同步技术,能够准确恢复接收到的单光子信号在发射单光子信号序列中的位置,是实现QKD的基础[9]。
在QKD系统中,使用的时间同步方法一般有三种:GPS系统、电同步和光同步。与光同步相比,前两种需要较多的硬件设备,增加了系统的复杂性和投入成本。因此对于已建成的卫星中继洲际量子通信网络和已成功发射的“墨子号”科学实验卫星,均使用光同步的时间同步方法。在星地自由空间链路中,通常采用提高系统发射频率的方法,以降低因光链路不稳定所导致光信号接收损耗的影响。然而目前光量子波包发射频率已提升至百兆量级,使得恢复光量子波包位置的难度提升。并且已发射的“墨子号”卫星的时间同步方案,是将数据采集和时间同步作为两个分立的步骤执行,执行周期较长,不利于未来的实际应用。为了改进上述不足,本文实现了一种适用于高发射频率的QKD接收系统,且本系统集成了数据采集和时间同步功能。在QKD接收系统中,接收端需具备高精度时间测量功能,以提高所记录光量子波包到达的时间精度。同时卫星与地面的相对运动会产生多普勒效应,影响量子信号的接收频率,并且接收端探测到的四路光量子波包在经过基于BB84协议[10]设计的光学模块时所途经的链路存在差异,为消除该部分影响,需对测得的时间值进行多普勒效应修正,并对四路差异值进行补偿。基于此,本文实现了一种星地量子信号同步方案,以满足量子传输通信过程中高频率光量子波包条件下接收端的量子信号同步需求。
1 方案设计
1.1 方案概述
所提出方案主要有两个方面的技术难点,精度达52.4 ps的高精度时间测量和时移量达14 kHz的多普勒修正。高精度时间测量的技术难点主要是由于采用FPGA加法器进位链(延迟链)资源进行高精度时间测量时,FPGA长时间的运行会使时钟产生漂移现象,导致所探测的时间信息存在误差。为保证高精度时间测量结果,利用短时间内(小于1 s)漂移所导致的时间误差可忽略不计的特点,在卫星端产生同步信号作为编号对发射的一段光量子波包进行时间位置标定,并使用经典信道在接收端恢复出同步编号(N),以消除时钟漂移对时间测量精度的影响。同时,卫星与地面站之间的高速相对运动产生多普勒效应,使接收端探测到的量子信号频率发生改变,影响时间同步结果。采用多普勒修正方案,利用同步信号和同步编号,通过收发双方的同步信号时间比可实现量子信号频率校准,获得准确的位置信息。针对以上技术难点,设计了“高精度时间测量”和“多普勒修正”两个主要功能模块,其系统结构框图如图1所示。
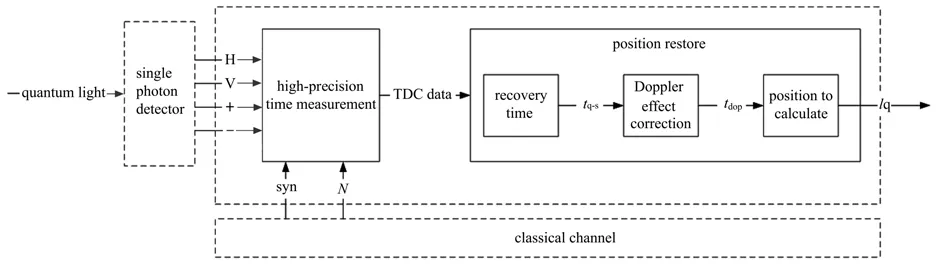
图1 基于FPGA的时间同步方案原理图Fig.1 Schematic diagram of time synchronization scheme based on FPGA
在系统中,接收到的光量子波包经单光子探测器响应获得四路电信号分别为“H”、“V”、“+”、“-”,将四路电信号以及同步信号通过加法器延迟链进行高精度时间测量得到时间数字转换(TDC)的数据。并利用位置恢复功能模块恢复接收到的光量子波包在发射端光量子波包序列中的位置,过程包括三部分:将获得的TDC数据进行时间恢复,得到量子信号相对同步信号的时间值tq→s;进行多普勒修正得到tdop,即实际卫星发射光量子波包相对同步信号的时间值;通过位置计算获得与发射光量子波包一致的位置信息lq。
1.2 高精度时间测量
如图1所示,为解决高精度时间测量模块时钟飘移对时间同步的影响,首先从经典信道恢复出同步编号,产生一个同步信号,使用高精度时间测量模块对同步信号进行测量,得到同步编号到达地面的时间值;其次,将同步编号嵌入到每一个TDC数据中,标记地面探测到的光量子波包和同步信号对应的同步编号;最后,采用“粗”时间测量和“细”时间测量相结合的方法,使用FPGA内部专用的加法器延迟链资源,完成高精度时间测量功能[11],得到高精度时间测量TDC数据,其系统设计框图如图2所示。
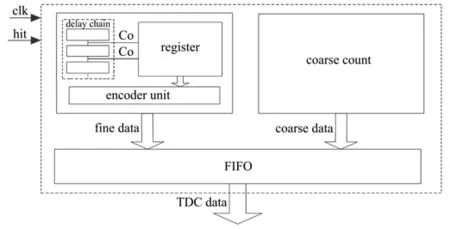
图2 高精度时间测量系统设计框图Fig.2 Block diagram of high-precision time measurement system design
1.3 位置恢复
1.3.1 时间恢复
在进行恢复时,为得到光量子波包和同步信号到达地面的时间值,需要对高精度时间测量数据进行解析,恢复出时间信息。高精度时间测量数据格式由同步编号、粗计数、细计数和通道号四部分组成,其中同步编号即为同步信号的编号;粗计数为系统时钟的计算值,从零开始累加,系统复位时清零;细计数为一个系统时钟周期内,脉冲信号在加法器延迟链中经过的通道数;通道号为单光子探测器的脉冲响应编号。时间恢复的公式可表示为

式中:Tclk为高精度时间测量模块的系统时钟,ncoarse为粗计数值,Bin为脉冲信号经过单个加法器的延迟时间值,nfine为细计数值。
在时间恢复过程中,得到了光量子波包的时间值和同步信号的时间值。计算出当前光量子波包相对于当前同步信号的位置信息,结合同步编号即能准确恢复出地面的位置信息。因此首先计算出光量子波包相对同步信号的时间差值

式中tq、ts分别为用(1)式计算的接收端光量子波包探测的时间值、当前同步编号对应的同步信号的时间值。
理想情况下,依据

即能恢复出地面的位置信息,式中:lq为接收端探测到光量子波包的时间位置,Tq为载荷光量子波包的发光周期,N为接收端恢复出的同步脉冲编号,Qq为每一个同步脉冲对应的载荷发光数。然而由于卫星与地面存在着多普勒效应,且相对于同步信号而言,四路光量子波包途经的链路存在着差异,这些原因均导致tq→s相对于实际值存在着误差,因此需要对tq→s进行进一步处理。
1.3.2 多普勒修正
多普勒修正阶段对tq-s数据进行进一步处理,以降低多普勒效应对收发两端时间同步的影响。在进行方案设计时,需考虑星地QKD的特殊性,即自由空间信道是不稳定的。当轨道存在云层遮挡时会出现短时间的数据丢失,因此在进行多普勒修正系数计算时,结合同步编号和两个同步信号间的时间值,设计了如下的计算方法

式中:Tdop为多普勒修正系数,Ts为同步信号周期,tsn为接收端当前同步信号的时间值,tsn-1为接收端上一个同步信号的时间值,Δn为当前同步信号与上一同步信号的同步序号差值。初始时刻,n=1时,tsn-1的值按0进行计算。
在(4)式中,当自由空间信道不稳定时,依然可以得到多普勒补偿系数。多普勒修正后的时间值可表示为

1.3.3 位置计算
位置计算阶段利用多普勒修正后的时间数据tdop,结合四路延迟值ΔTdm(m=1,2,3,4分别对应“H”、“V”、“+”、“-”相对于同步信号到达高精度时间测量模块的延迟值)、载荷光量子波包的发光周期Tq、同步编号N和每一个同步编号对应的光量子波包个数Qq,即可得到接收端探测光量子波包准确的位置信息lq,可表示为

2 实验验证
2.1 高精度时间测量功能
在所提出的量子信号同步方案中,高精度时间测量是该方案的核心功能。高精度时间测量模块使用Intel公司Stratix IV系列FPGA的EP4SGX230KF型号的芯片进行设计,存在五条加法器延迟链,系统时钟为100 MHz,每条延迟链包含300个延迟单元。为验证所设计高精度时间测量模块的性能,对高精度时间测量模块进行了测试,实验装置示意图如图3所示。
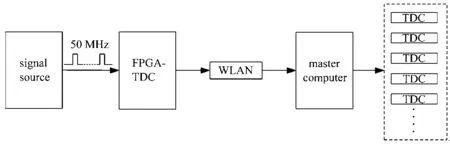
图3 高精度时间测量模块实验装置示意图Fig.3 Schematic diagram of high-precision time measurement experimental equipment
在测试时,认为信号源所输出的信号是标准的,则以高精度时间测量模块(FPGA-TDC)所探测到的第一个脉冲信号为起始点。在理想情况下,两个相邻脉冲间的时间差值即为信号源的调制周期值(20µs),然而由于高精度时间模块在工作时存在晃动,导致相邻两个脉冲间的时间差值在20µs上下晃动。为进一步分析高精度时间测量模块的晃动,使用后一个脉冲时间值减去当前脉冲的时间值,再减去信号的周期值,得到时间差值Δt(理想条件,该值为0),对Δt进行拟合,得到抖动范围如图4所示。
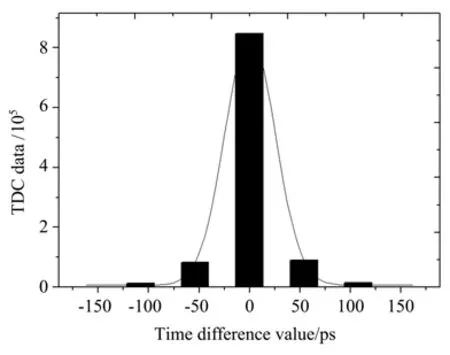
图4 高精度时间测量抖动范围Fig.4 High-precision time measurement of shaking range
如图4所示,对1048576个TDC数据处理后,得到Δt时间值在-162~162范围内晃动,Δt的均方差值为36.45 ps。同时为测量模块中信号经过单个加法器的时间值,统计了90000个高精度时间测量数据的细计数,其细计数最大值为191道,即在一个系统时钟周期内,信号在加法器延迟链中所经过的加法器个数最大值为191个,因此在系统周期10 ns下,信号经过单个加法器的时间值约为52.4 ps,该精度对于分辨发射周期为1.6 ns的量子信号是足够的。上述测试所设计的高精度时间测量模块,在百兆量级的光量子波包发射频率下可以满足接收端光量子波包和同步信号的时间测量需求。
2.2 量子信号同步方案验证
为验证“星地量子密钥分发量子信号同步方案”的可行性,在实验室搭建了星地QKD的模拟系统,对所提出方案的性能进行验证。在模拟系统中,发送端光源波长为850 nm、发射频率为625 MHz,接收端单光子探测器的暗计数为150 cps、死时间为30 ns,经典信道为激光信道,量子信道的链路衰减设置为40 dB,接收端所探测到的总量子信号数约为55000 cps。
在量子信号同步系统中,同步精度越高所探测的有效量子信号计数率越高,筛选码的误码率越低。如图5、6所示,有效探测计数约为50000 cps,占总探测计数的90%左右,每100 kbit的筛选码误码率约为1.78%,满足QKD系统对同步精度的要求。因此在卫星发射高频率光量子波包条件下,所提出的量子信号同步方案能较准确恢复出接收端所探测到的光量子波包的时间位置信息,并且卫星与地面也能依据该位置信息完成各自筛选码的生成,从而完成量子传输通信过程中的筛选码提取。
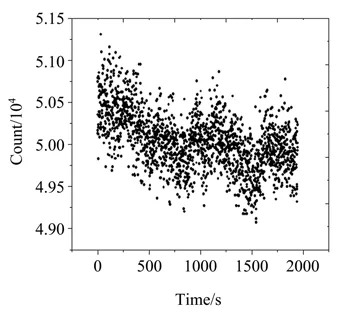
图5 有效量子信号计数率Fig.5 Count rate of effective quantum signal
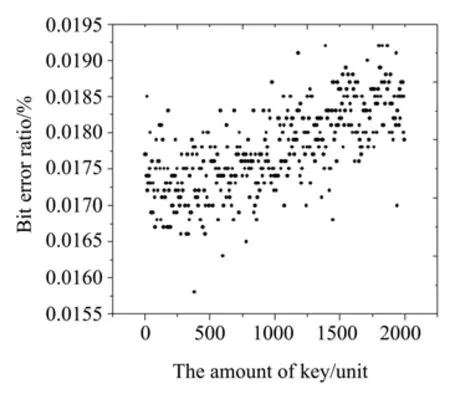
图6 筛选码误码率Fig.6 Bit error ratio of sifted code
3 结论
基于FPGA平台实现了一种量子信号同步方案,针对时间测量的精度和位置恢复提出优化策略。采用基于加法器延迟链的高精度时间测量技术,对探测的量子信号进行高精度时间测量,其时间测量精度达到52.4 ps。利用测量的时间值进行多普勒修正,精确地恢复出接收端所探测光量子波包的时间位置信息,获得较好的同步效果,实现量子密钥分发。在量子通信领域,所提出方案既适用于高速实时星地QKD系统,也适用于地面的高速QKD方案,具有广泛的应用范围。
