永磁同步电机系数自整定速度补偿控制方法
2022-06-10宋哲杨军陶涛黄建梅雪松
宋哲,杨军,陶涛,黄建,梅雪松
(1.中国航天科工集团北京自动化控制设备研究所,100074,北京;2.西安交通大学陕西省智能机器人重点实验室,710049,西安;3.西安交通大学机械制造系统工程国家重点实验室,710049,西安)
随着工业控制领域生产和应用的迅速发展以及日趋多样化,对于不确定的参数变化和外界扰动,要求永磁同步电机(PMSM)伺服系统应具备良好的适应性和抗扰性[1-3]。然而,在PMSM实际运行过程中,系统所带负载转矩的变化会对电机的速度造成较大的波动,降低电机的控制性能[4-6]。常用的方法是在PMSM运行中及时准确的获取负载转矩,并对其加以适当的控制或补偿,抑制转矩变化引起的速度波动。目前,PMSM负载转矩的获取方式主要包括测试测量和估计辨识两大类。其中,转矩测量方法主要是通过添加转矩传感器的方式来进行。但随着机器人、数控机床等高端装备向着一体化、微小型化发展的趋势[7],受限于操作空间、测量成本和精度,实际应用中通常采用估计辨识的方法获取电机的负载转矩。
一般来说,负载转矩的辨识方法主要有直接计算法、状态观测器、卡尔曼滤波器和滑模观测器等。直接计算法简单易于实现,但容易产生强烈的干扰,在实际中应用较少[8]。卡尔曼滤波器辨识精度高,对噪声具有很强的抵抗能力,但算法相对复杂,计算量大,对数字处理器的要求较高[9]。滑模观测器的动态响应快、抗干扰能力强,而且具有很强的鲁棒性,但是存在无法克服的高频抖振问题[10-11]。状态观测器按照维数可以分为全维状态观测器和降维状态观测器,它的输入状态变量容易测量,转矩观测的速度较快,误差较小,是目前常用的转矩辨识方法[12]。此外,一些人工智能算法如模糊控制[13]、神经网络[14]、遗传算法[15]等也被逐渐应用于转矩扰动的估计与控制,并且取得了一定的效果,但这些方法大都存在算法复杂、计算量大的特点,尚处于研究阶段,在实际工程中应用较少。
因此,在PMSM伺服系统受到负载转矩的外部扰动时,通过转矩观测器和前馈补偿来及时削弱转矩扰动对电机转速的影响,是常用的控制方式。文献[16]将自抗扰控制器和负载观测器相结合,设计了二阶速度控制系统,通过对负载扰动的观测和补偿,提高了PMSM电动履带车辆的抗扰动能力。文献[17]将系统未建模的不确定性干扰考虑在内,设计了带有转矩观测器的PMSM模糊滑模速度控制器,有效抑制了抖振,提高了电机运行的鲁棒稳定性。为使系统在不同负载条件下稳定运行,文献[18]设计了非线性扩张状态观测器用于PMSM无传感速度控制,通过转矩估计及补偿,在全速范围减小了转速波动。目前已有的研究成果提高了PMSM控制系统的抗转矩扰动性能,但并未考虑系统中转动惯量对转矩辨识的影响,没有对转矩辨识中转动惯量的影响机理进行研究和分析,更没有对此提出行之有效的控制策略。
对此,本文研究了PMSM负载转矩辨识与自适应速度补偿,并提出一种系数自整定的速度补偿控制方法。首先,采用状态空间表示法设计了PMSM负载转矩的降维状态观测器,对负载转矩进行实时辨识与估计。然后,将转矩辨识值补偿到PMSM电流控制器的输入端,实现自适应速度补偿,以此来提高对负载转矩的抗扰性。考虑到系统中转动惯量的时变特性,分析了转动惯量的变化对转矩观测器辨识结果的影响规律,提出一种基于sigmoid函数的补偿系数自整定的控制方法,用于提高自适应速度补偿对转矩辨识结果的鲁棒性,减小转矩辨识结果对前馈补偿的影响。最后,通过实验对本文所提方法的正确性和有效性进行了研究和验证。
1 PMSM自适应速度补偿
1.1 降维状态观测器设计
根据PMSM的工作原理,建立其降维动力学状态方程[19-21]
(1)

针对式(1)的降维动力学状态方程,设计一个降维状态观测器对负载转矩进行观测
(2)

由式(1)减去式(2),可得降维状态观测器的误差状态方程
(3)

(4)
s2-(α+β)s+αβ=0
(5)
由待定系数法,联立式(4)和式(5),可得
(6)
由PMSM机械运动方程可知,黏滞摩擦系数Bm值一般很小,可忽略不计,即Bm=0。为了控制方便,容易工程实现,通常取α=β,则式(6)可以改写为
(7)
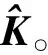

图1 特征方程根轨迹Fig.1 Root locus of characteristic equation
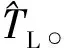
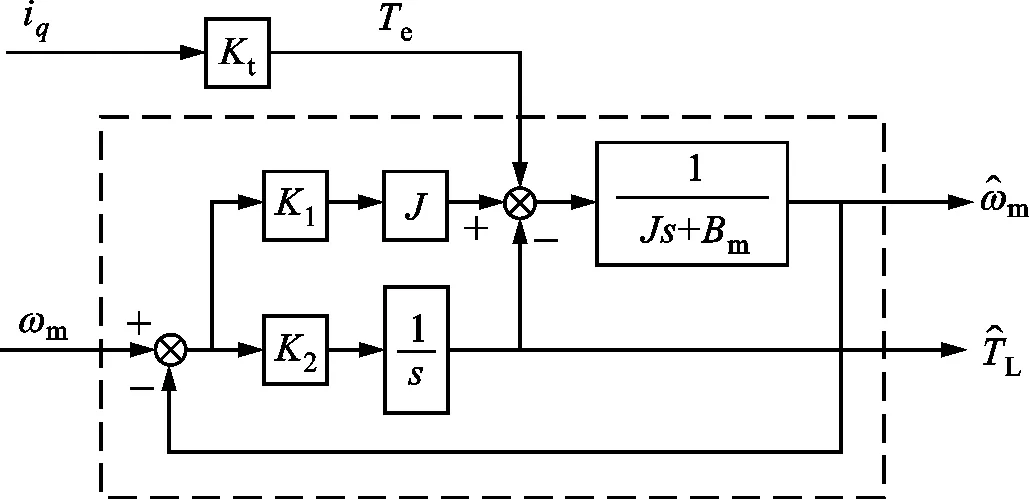
图2 负载转矩降维观测器原理框图Fig.2 Block diagram of load torque dimension reduction observer
在PMSM伺服系统中,降维状态观测器通过离散递推的方式来实现数字化控制,假设观测器辨识算法的控制周期为T,对式(1)进行离散化可得
ωm(k+1)=
(8)
式中T为辨识算法的控制周期。
结合式(8)将式(2)进行离散化可以得到电机转速和负载转矩观测值的递推公式
(9)

1.2 自适应速度补偿


图3 PMSM自适应速度补偿控制框图Fig.3 PMSM adaptive speed compensation control block diagram
根据自动控制原理,可得PMSM自适应速度补偿控制的补偿公式
(10)
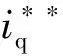
通过调节补偿系数β1,利用负载观测器的辨识和前馈补偿就可以校正因负载突变而引起的速度变化。如果参数设置合理,当补偿系数β1取临界值β1_full时,静态误差消失,此时理论上可完全消除负载转矩扰动带来的速度影响,称为“全补偿”。当β1<β1_full时,称为“欠补偿”,扰动补偿时速度会存在静差;当β1>β1_full时,称为“过补偿”,此时电机出现转矩扰动时,补偿后速度曲线上翘,容易引起系统不稳定。一般情况下,为避免出现“过补偿”现象,通常将补偿系数设置在“欠补偿”状态。
2 惯量对转矩观测的影响
以TI公司的TMS320F2812为主控芯片搭建实验平台,如图4所示。实验平台主要包括伺服电机、联轴器、转速转矩传感器、磁粉制动器、信号发生器、功率放大器和示波器7部分。使用的永磁同步电机具体参数如表1所示,其中直流母线电压Udc=310 V,开关频率fc=8 kHz。电机和转速转矩传感器通过联轴器实现同轴旋转;信号发生器的信号经功率放大器转换后控制磁粉制动器,为电机提供负载转矩;示波器用于显示各个波形。实验数据以通信的方式由DSP控制芯片传送至计算机。
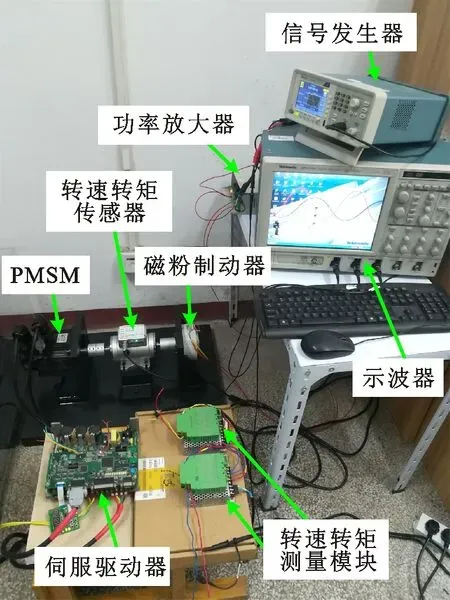
图4 实验平台Fig.4 The experimental platform
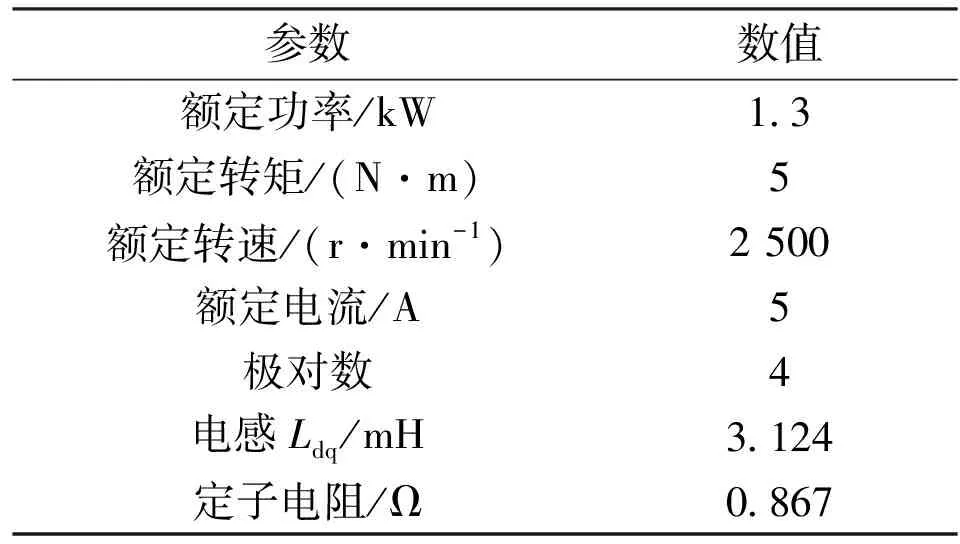
表1 PMSM参数
2.1 参数敏感性分析
为了验证状态观测器中转动惯量对负载转矩辨识结果的影响,分别将系数矩阵中转动惯量的值取为0.2J和5J,进行实验研究,并与真实转动惯量J下的辨识结果对比分析。实验中伺服系统的转动惯量包括电机转子惯量,联轴器惯量,转速转矩传感器转动轴惯量和制动器惯量,折算出来为1.51×10-3kg·m2。电机稳定运行在1 000 r/min,突加负载转矩为恒定的4 N·m,不同转动惯量的转矩辨识结果如图5所示。由图5(a)可以看出,降维状态观测器能够快速准确地辨识出PMSM伺服系统的负载转矩,而且效果较好,转矩辨识值与施加负载转矩的变化趋势一致,转矩辨识的响应时间约为70 ms,辨识误差约为5%。对比图5(b)、图5(c)可以看出,当负载转矩观测器的系数矩阵中转动惯量偏离其真实值的时候,负载转矩的辨识结果出现较大超调或偏差。具体表现为当惯量取值小于真实值的时候,转矩辨识的结果出现较大超调;当惯量的取值大于真实值的时候,转矩辨识收敛减缓,辨识过程中容易出现偏差。

(a)转动惯量为J时的辨识结果

(b)转动惯量为0.2J时的辨识结果

(c)转动惯量为5J时的辨识结果图5 转动惯量对转矩辨识的影响实验波形Fig.5 Influence of inertia on torque identification experimental waveforms
2.2 补偿系数自整定

(11)
式中:a>0,用于调节sigmoid函数的斜率;M>0、N>0分别用于设置sigmoid函数的幅值和偏置。


图6 补偿系数sigmoid函数曲线Fig.6 Compensation coefficient curves of sigmoid function
3 实验研究
针对伺服系统的惯量时变场合,如工业机器人系统,转动惯量随机械臂的运动而改变,控制中设置的转动惯量通常与真实值之间存在一定的偏差,或大或小。为了验证提出的自整定补偿系数控制方法的正确性和有效性,分别将转矩观测器的系数矩阵中转动惯量的值设置为0.2J、5J和真实值J,进行实验研究,并与常规的固定补偿系数控制方法的实验结果对比分析。实验平台如图4所示,实验中伺服系统的转动惯量包括电机转子惯量,联轴器惯量,转速转矩传感器转动轴惯量和制动器惯量,折算出来为1.51×10-3kg·m2。实验平台中磁粉制动器的许用转速为1 500 r/min,考虑到实验的安全性和实验数据的可靠性,本文以许用范围内的常用中间速度为例,进行了实验研究。由于突加负载转矩和突减负载转矩的情况完全类似,实验中仅针对突加负载转矩的常用情况进行了研究,突减负载转矩的情况不再复述。为了验证惯量变化对转矩辨识速度补偿的影响,提高PMSM速度控制的抗转矩扰动性能,对比分析电机稳态运行中的动态转矩扰动,动态性能指标选用调节时间和超调量来进行说明。实验中电机稳定运行在1 000 r/min,突加负载转矩恒定为4 N·m,实验结果如图7~图9所示。

(a)固定补偿系数的实验结果

(b)自整定补偿系数的实验结果图7 转动惯量为J时的实验波形Fig.7 Experimental waveforms at inertia J
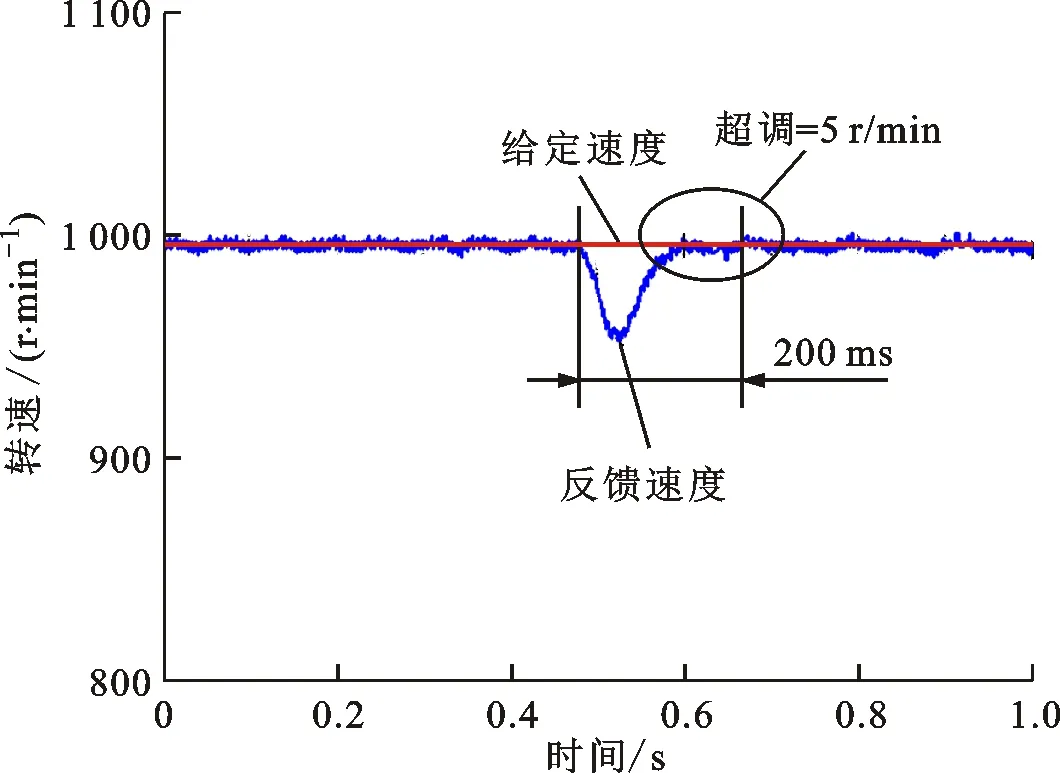
(a)固定补偿系数的实验结果

(b)自整定补偿系数的实验结果图8 转动惯量为0.2J时的实验波形Fig.8 Experimental waveforms at inertia 0.2J
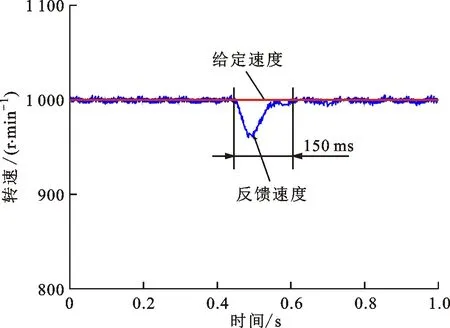
(a)固定补偿系数的实验结果

(b)自整定补偿系数的实验结果图9 转动惯量为5J时的实验波形Fig.9 Experimental waveforms at inertia 5J
当负载转矩降维状态观测器的系数矩阵中转动惯量偏离其真实值时,负载转矩的辨识结果会出现较大超调或偏差,由此影响速度补偿的效果。但是,相比常规固定补偿系数的控制方法,提出的自整定补偿系数的控制方法由于可以在线调节,动态调整,自适应速度补偿的效果更好。当转动惯量取真实值J时,固定补偿系数的速度调节时间约为120 ms,而自整定补偿系数的速度调节时间约为100 ms,如图7所示。当转动惯量取0.2J时,固定补偿系数的速度超调约为5 r/min,速度调节时间约为200 ms;而自整定补偿系数的速度超调约为2 r/min,速度调节时间约为170 ms,如图8所示。当转动惯量取5J时,固定补偿系数的速度调节时间约为150 ms,而自整定补偿系数的速度调节时间约为130 ms,如图9所示。
由以上实验结果可以看出,当转矩观测器的惯量参数偏离其真实值导致负载转矩的辨识结果出现较大误差时,提出的补偿系数自整定的控制方法能够根据转矩辨识结果在线调节补偿系数,减小了因惯量偏离真实值而导致转矩辨识出现超调或偏差时,通过前馈补偿对速度控制造成的冲击和振荡,有效提高了PMSM伺服系统的速度控制性能。
4 结 论
为了提高永磁同步电机速度伺服系统的抗转矩扰动性能,提出一种基于sigmoid函数的补偿系数自整定的控制方法,得到以下结论:
(1)降维状态观测器能够准确辨识出PMSM伺服系统的负载转矩,动态响应较快,稳态误差较小,通过自适应速度补偿可以有效地抑制因负载转矩变化而引起的速度波动;
(2)当转矩观测器的系数矩阵中转动惯量偏离其真实值时,负载转矩的辨识结果将会出现较大超调或偏差,通过前馈补偿至电流环输入端时,容易造成速度的冲击和振荡,影响电机的运行性能;
(3)提出的基于sigmoid函数的补偿系数自整定的控制方法能够根据转矩辨识结果在线调节补偿系数,减小了转矩辨识结果对前馈补偿的影响,增强了自适应速度补偿对转矩辨识结果的鲁棒性,提高了PMSM伺服系统的控制性能。
