基于涡旋电磁波雷达的人体目标步态精细识别
2022-06-10袁航罗迎李开明陈怡君张群
袁航, 罗迎,2, 李开明, 陈怡君, 张群,2
(1.空军工程大学 信息与导航学院, 陕西 西安 710077; 2.复旦大学 电磁波信息科学教育部重点实验室, 上海 200433;3.西安电子科技大学 雷达信号处理国家重点实验室, 陕西 西安 710071; 4.武警工程大学 信息工程学院, 陕西 西安 710086)
0 引言
由于雷达侦察距离远,可全天时工作,受极端天气影响较小,雷达成为主要的侦察手段之一。在身份检测[1]、医疗救助[2]、军事[3]等领域,关于基于雷达对人体目标步态识别进行了诸多研究,也取得了较多的成果。该类识别方法往往是基于目标径向运动产生的线多普勒效应[4],利用不同方法提取特征,输入分类器中获得结果。常见的特征有散射特征、多普勒特征、平动特征等。文献[5]将卷积神经网络作为分类器,将回波时频图的幅度作为输入,获得人体目标的分类结果。文献[6]通过距离- 多普勒帧和峰值搜索算法提取目标平动、多普勒、雷达散射截面积(RCS)特征,再将机器学习模型作为分类器,获得结果。文献[7]首先获取目标雷达回波,再通过改变短时傅里叶变换的窗长,从而得到不同窗口长度下的时频图,再将时频图输入到双通道卷积神经网络中,最终获得识别结果。上述方法均使用传统的平面电磁波雷达,并在此基础上进行研究,其目标均为差异较大的人体运动(如行走、奔跑、跳跃、蹲下等)[8]。当人体运动轨迹相近(如摆双臂行走、摆单臂行走、不摆臂行走)时,多普勒效应很相似,传统方法难以准确分类目标。
与传统电磁波相比,由于涡旋电磁波拥有螺旋形相位波前分布,其含有独特的轨道角动量,获取目标信息的能力显著提高[9-10]。涡旋电磁波照射目标时,目标运动会产生线多普勒效应和角多普勒效应[11],线多普勒为雷达与目标的径向相对运动引起的频率偏移;角多普勒为雷达与目标的方位角相对运动引起的频率偏移。当径向运动相似时,利用角多普勒可取得更好的效果。由于涡旋电磁波的独特性质,众多涡旋电磁波生成方法被提出,常见的生成装置有均匀圆环阵(UCA)[12]、相控阵[13]、螺旋反射面[14]等。涡旋电磁波雷达大多被应用于成像领域,取得了不错的效果[15-17]。现有基于涡旋电磁波的人体步态识别研究较少,文献[18]利用单频涡旋电磁波照射目标,利用短时傅里叶变换获得时频图,将时频图输入到分类器中获得结果。该方法直接利用单频涡旋电磁波,并未将线多普勒与角多普勒分离。与线多普勒相比,角多普勒较微弱,易淹没在线多普勒中,回波中的角多普勒并未被很好利用。
针对上述问题,本文利用线性调频涡旋电磁波照射目标,获得双模态回波,利用双通道卷积神经网络模型预测结果。首先建立了人体目标的涡旋电磁波雷达回波模型;然后将回波变换到距离域,利用双模态回波的互相干涉,抑制线多普勒,获得角多普勒信息;再利用短时傅里叶变换获得角多普勒和线多普勒的时频图,将时频图的幅度值作为特征,输入到双通道卷积神经网络模型中,从而获得分类结果。仿真结果表明,该方法可以对人体步态进行精细识别,并对噪声具有一定的鲁棒性。
1 涡旋电磁波雷达回波模型
近年来,由于涡旋电磁波的独特性质,多种涡旋电磁波生成方法被提出。本文采用最常见的UCA装置来生成涡旋电磁波。图1所示为UCA与目标的几何关系。图1中,Oxyz为空间直角坐标系,在Oxy平面上存在一个以O为圆心、半径为a的圆周,Orθφ为球坐标系,点目标p位于(x0,y0,z0)处,v为点目标p的速度矢量。Q个天线在圆周上等间距排列,第q个天线的相移为exp(iαφq),α为模式数,φq=2πq/Q,q=0,1,…,Q-1,雷达视线方向为z轴正半轴,i为虚数。
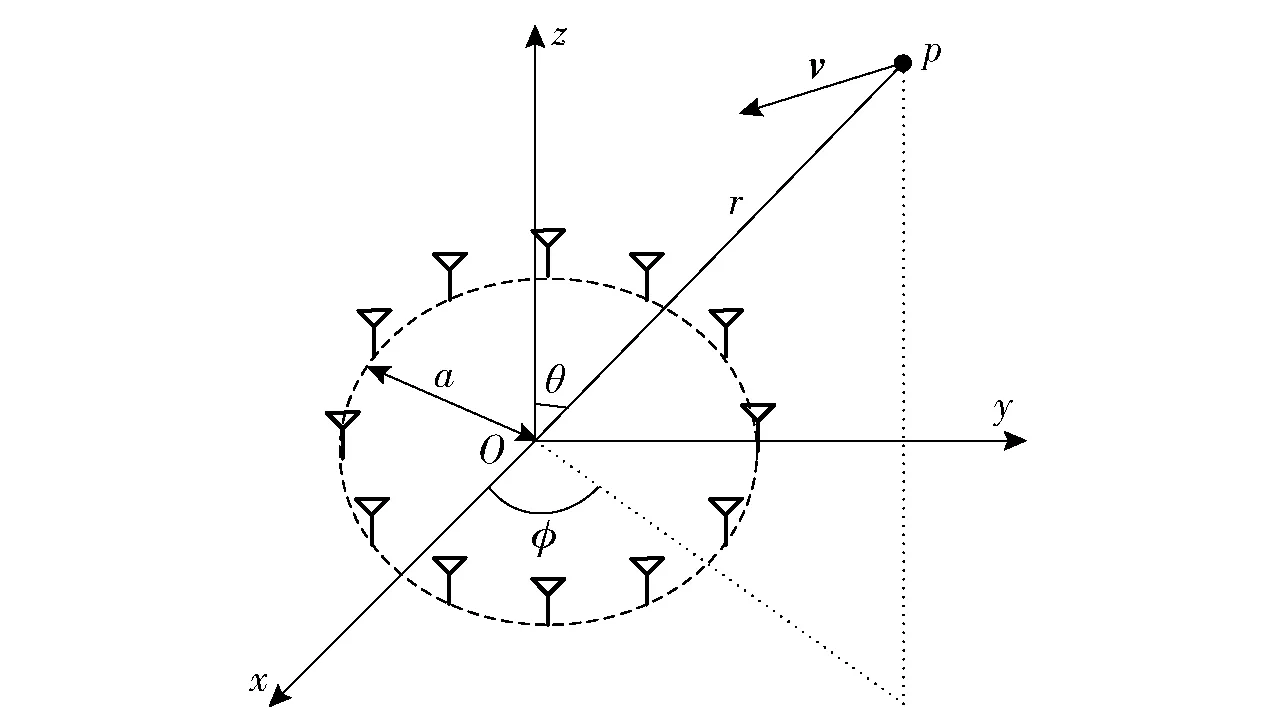
图1 UCA与目标几何关系示意图Fig.1 Geometric relationship between UCA and target
则点目标p的运动轨迹为
(xp(t),yp(t),zp(t))=(x0+vxt,y0+yyt,z0+vzt)
(1)
式中:vx、vy、vz分别为速度矢量v在x轴、y轴、z轴3个方向的分量。p点在球坐标系(r,θ,φ)下的位置为
(2)
式中:θp(t)∈[0,π];φp(t)∈[0,2π)。雷达发射线性调频信号,第p个散射点的点回波[14]可表示为

(3)
式中:σp为散射系数;Jα为第一类α阶贝塞尔函数;k(t)=2π(fc+γt)/c,fc为载波频率,γ为调频率,c为光速;τp(t)=2rp(t)/c,rp为第p个散射点到雷达的距离;TP为脉冲持续时间;rect(·)为矩形窗函数。将s(t,α)乘以参考信号sref(t)=exp (-i2π(fct+0.5γt2)),获得sp(t,α),其表达式为

(4)
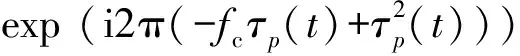
(5)
假设在ts时刻,散射点p位于空间直角坐标(x0,y0,z0)处,且在时间Δt内的瞬时速度矢量为(vx,vy,vz),则该时刻的瞬时角多普勒频率fA[11]为
(6)
角多普勒频移由目标位置矢量和速度矢量到Oxy平面的投影决定。
2 人体回波生成
人体可视为由多个不规则区域组成的集合,当雷达信号照射人体时,多个区域的回波相互叠加,雷达散射截面积的计算异常复杂。为便于分析及仿真,可利用椭球体近似模拟人体各区域[6]。此时人体被简化为14个椭球体(见图2),简化模型[6]如图2(a)所示。图2(b)中,Los为雷达视线方向,αR、βR为雷达视线方向在球坐标系下的角度,dn为第n个椭球体长轴的方向矢量,φR,n为椭球体长轴与雷达视线方向的夹角。

图2 椭球体模型Fig.2 Ellipsoid model
雷达视线方向为
Llos=[cosαRcosβR,sinαRcosβR,sinβR]
(7)
则φR,n可由(8)式计算:
(8)
式中:〈〉表示内积;‖‖2为2-范数。在全局坐标系下,第n个椭球体的RCS计算公式[19]为
(9)
式中:an、bn、cn为第n个椭球体的3个半轴。设雷达到第n个椭球体质心的矢量为mn。由于角多普勒与目标方位角有关,定义两个单位向量L2、L3,构成雷达平面,
L2=[-sinαR,cosαR,0]
(10)
L3=[-cosαRsinβR,-sinαRsinβR,cosβR]
(11)
目标投影到L2、L3的大小为
p2,n=〈mn,L2〉
(12)
p3,n=〈mn,L3〉
(13)
可计算出
(14)
(15)
式中:θn(ts)为第n个椭球体球心矢量的俯仰角。
则人体14个区域总回波为
(16)
3 回波信号处理


(17)
式中:H(f)=sinc(Tpf)⊗F(f),⊗为卷积操作。H(f)与sinc函数的性质类似,其绝对值为
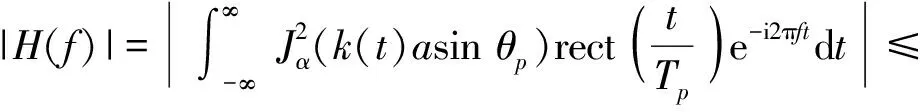
(18)
(19)
为获取回波中的角多普勒信息,需要利用双模态回波
(20)
线多普勒和角多普勒相互耦合,为提取目标角多普勒,将(20)式中的双模态回波共轭相乘,

(21)
式中:上标*代表共轭操作。
当γτp(ts)≈γτk(ts)时,设有L个区域处于同一距离单元,此时f=γτl(ts),l为某个距离单元,距离对于幅度的影响较小。该距离单元的信号可表示为
(22)
目标时频图如图3所示,图3(a)为目标线角多普勒混合时频图,图3(b)为目标线多普勒时频图,图3(c)为目标角多普勒时频图。在分离前,角多普勒对时频图的影响较小。由于共轭相乘操作,其线多普勒被抑制,角多普勒凸显。图3(c)中的波峰为目标手臂摆动引起的角多普勒频移,与线多普勒时频图相比,其信息更为突出。同时,为利用目标的线多普勒信息,将s(f,tm,α)作为线多普勒。
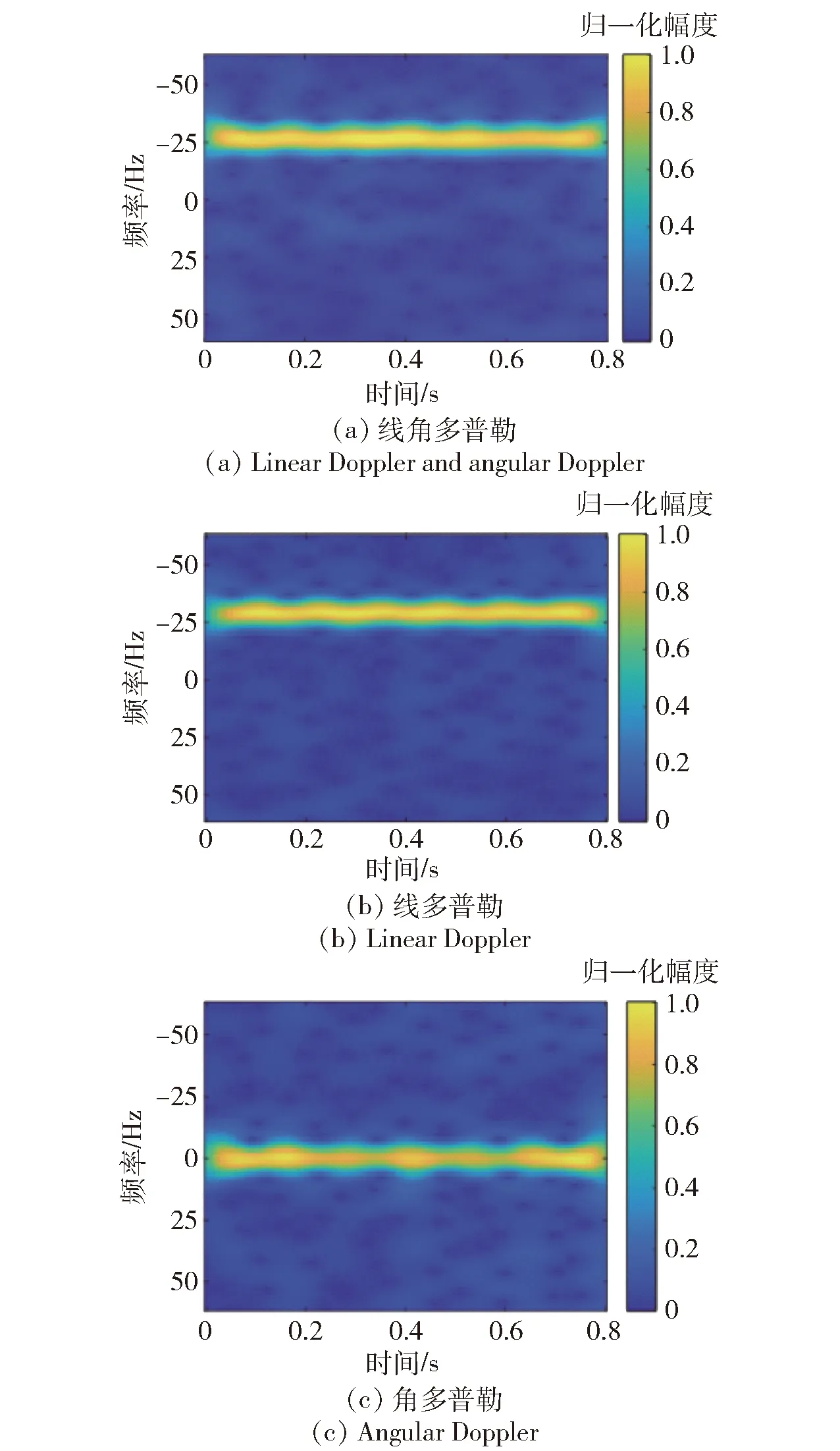
图3 时频图Fig.3 Time-frequency diagram
为更好地识别目标,需要对上述信号进一步处理,用时频图来表征信号。常用的时频变换方法有短时傅里叶变换、Gabor变换和小波变换等。文献[20]利用短时傅里叶变换来获得目标时频图,短时傅里叶变换的过程可表示为
(23)
式中:u的长度决定短时傅里叶变换的时频分辨率;w(·)为窗函数,不同窗函数有不同的效果。选择合适的窗长来表达目标的时频特性。
4 识别模型
近年来,卷积神经网络广泛应用于雷达图像分类任务中[19,21-22],取得了一系列较好的成果。现有的算法大多是在基于卷积神经网络模型的基础上,再将提取到的目标深层次信息输入到模型中,取得分类结果。本文利用的深度学习模型结构如图4所示。图4中,模型由卷积层、池化层、批规范化层、Softmax层和全连接层组成,主体部分为双通道的5层卷积神经网络;Conv代表一层卷积核大小为9×9、步长为1卷积层;批标准化(BN)为批规范层;ReLU为损失函数;Pool表示该层为池化大小和步长都为2的池化层;Concatenation为拼接操作,将两通道的输出拼接起来,输入到全连接层。
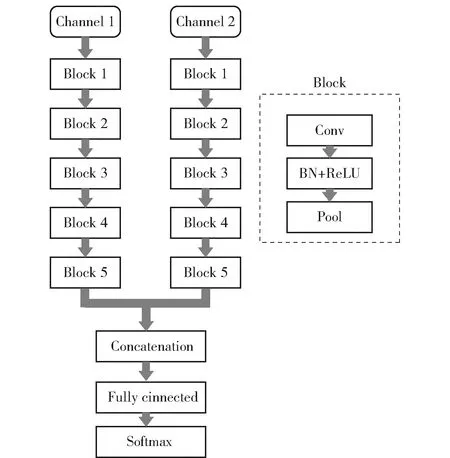
图4 识别模型Fig.4 Recognition model
算法分类过程可简单表述为:首先将时频图的幅度值输入到两个通道中,时频图经过5层网络后,拼接其输出,输入到全连接层中,最后将全连接网络的输入到Softmax层,获得分类结果。该模型的激活函数为ReLU函数。假设输入到Softmax函数的数组为zj,j=1,2,…,J,Softmax层的输出表达式为
(24)
Softmax层的输出为(0,1)范围内的值,该层输出之和为1。该数值可表征分类结果,其数值越接近1,代表某个目标为真的可能性越大。Softmax层输出的向量长度代表待分类目标数,若为1×3阶的向量,则代表模型对三类目标进行预测。为衡量预测输出与标签的差异,需要通过损失函数量化。先将目标标签以one-hot码表示,再通过损失函数计算损失,损失函数可表示为
(25)
式中:P(xj)为xj的实际概率分布;q(xj)为输入xj时模型分类结果。当实际概率分布和模型分类结果越接近,则损失越小。通过不断优化,预测正确率逐渐增大。算法流程图如图5所示,先对回波作关于快时间的傅里叶变换,在距离域分离信号;再利用双模态回波,对目标进行干涉处理,提取距离域的峰值信号;最后利用短时傅里叶变换,获得目标线多普勒和角多普勒时频图,将时频图输入到分类器中,获得分类结果。
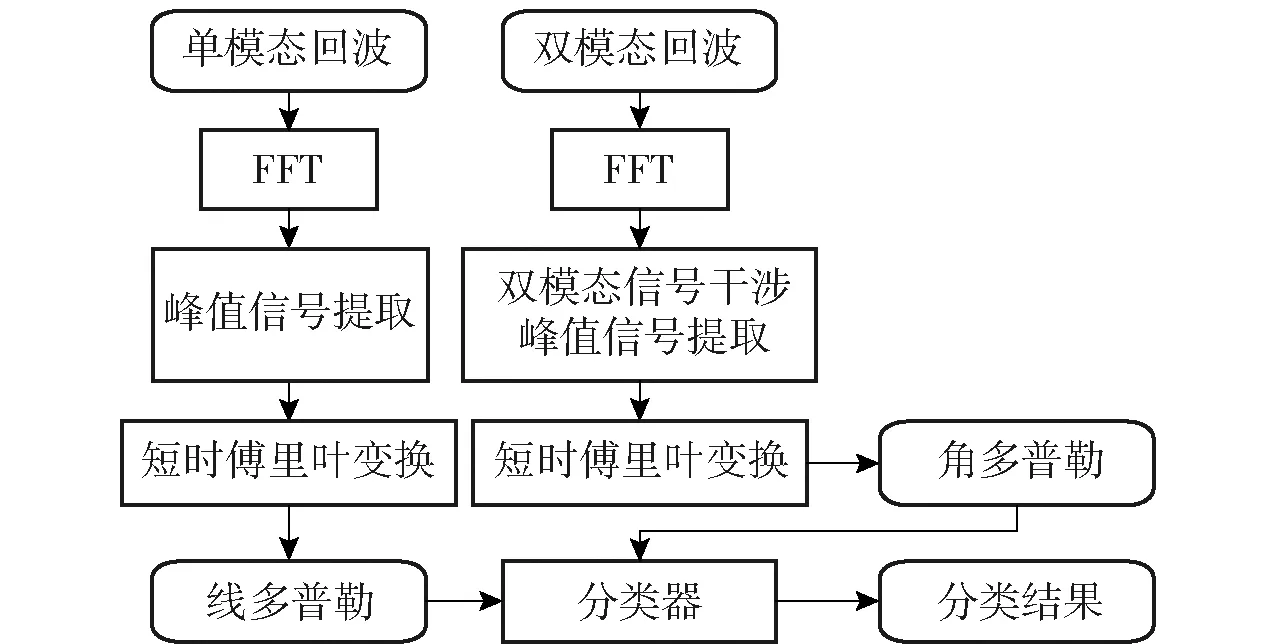
图5 算法框图Fig.5 Algorithm block diagram
5 仿真结果
雷达参数设置如表1所示。人体目标的身高设置为1.6~1.8 m,行走方向随机,行走速度为2~4 m/s,初始位置距雷达中心1 500~1 600 m,雷达视线方向为αR=0.5π rad,βR=0 rad。

表1 雷达参数Tab.1 Radar parameters

图7 目标时频图Fig.7 Time-frequency diagram of target
三类目标的行走过程如图6所示。目标1为正常摆双臂行走;目标2为右手相对静止,左臂正常摆动;目标3为双手置于胸前,与身体保持相对静止。三类目标的腿部动作一致,区别在于双手状态的不同。三类目标的时频图如图7所示,图7(a)、图7(b)、图7(c)为三类目标的线多普勒时频图。由于目标2和目标3手臂与身体相对静止,其多普勒效应与躯干相似,目标主体多普勒效应增强。从中可以发现:图7(a)和图7(b)的主体多普勒较为相似,背景不同,其多普勒频移主要由双臂摆动造成。由于目标3中双臂与身体相对静止;图7(c)的时频图更光滑,其多普勒频移主要由双腿摆动造成。图7(d)、图7(e)、图7(f)分别为三类目标的角多普勒时频图,与线多普勒相比,角多普勒呈现出更多信息。由于双臂同时摆动,图7(d)的角多普勒明显,时频图背景也较为复杂,一个周期内角多普勒存在两处峰值。图7(e)为摆单臂行走,其角多普勒时频图背景复杂度较低,角多普勒主要由腿部和单臂摆动造成,一个周期内角多普勒存在一处峰值。图7(f)为双臂静止行走,与图7(d)和图7(e)相比,其时频图背景最为简单,角多普勒主要由躯干移动和腿部摆动造成。

图6 不同时刻下的行走过程Fig.6 Walking process at different times
为验证将线多普勒、角多普勒分离的优势,仿真中将目标的线多普勒和角多普勒的混合信息、线多普勒和角多普勒分离信息和角多普勒信息输入到同一个识别模型中,从而获得不同输入下的分类结果,如表2所示。表2中,线角分离为分别利用线多普勒和角多普勒特征;线角混合为不将线多普勒和角多普勒分离[18],直接输入分类器中;角多普勒为只利用角多普勒信息,将线多普勒信息抛弃。由于角多普勒远小于线多普勒,线角混合的方法并不能取得最好的效果。同时,角多普勒并不能全面反映目标信息,只利用角多普勒的方法难以获得很好的分类性能。由于角多普勒中含有额外的目标信息,通过联立角多普勒信息和线多普勒信息,可以有效提高识别能力。将线多普勒和角多普勒分离后,有益于准确识别人体精细步态目标。

表2 仿真结果Tab.2 Simulated result
数据集共含有2 000个数据,目标1、目标2、目标3分别为666、667、667个。无噪声条件下的识别混淆矩阵展示在表3中,模型对1类目标的识别率最高,2类目标的识别率最低。在实际中,回波中必然存在各类噪声。为验证本文方法在有噪条件下的性能,为回波中加入复高斯白噪声,使信噪比为5 dB、10 dB、15 dB。对不同信噪比下表2方法的表现进行仿真实验,结果如表3所示。由表3可见,由于利用了目标在不同域的表示,线多普勒和角多普勒被输入到分类器中,其鲁棒性更好。
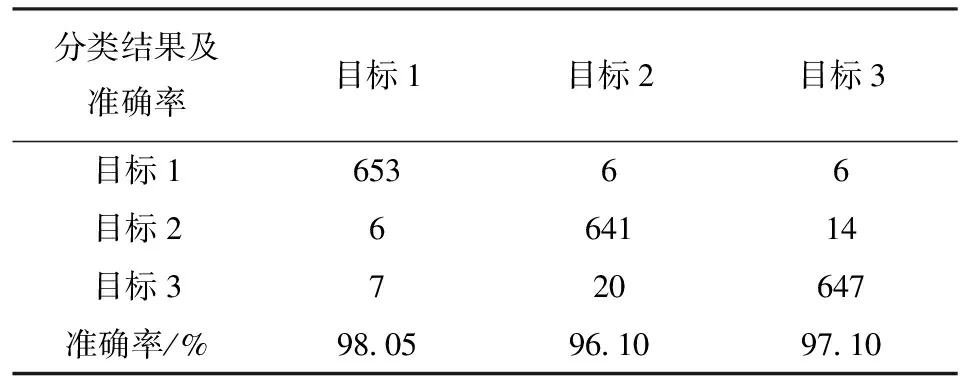
表3 无噪声下的识别混淆矩阵Tab.3 Recognition confusion matrix without noise


图8 角多普勒时频图Fig.8 Time-frequency diagram of angular Doppler

表4 相对位置对识别率的影响
6 结论
1)利用涡旋电磁波而不是传统电磁波,可提高人体步态精细目标的识别准确率。
2)将涡旋电磁波中的线多普勒信息和抑制线多普勒后的角多普勒信息分别作为输入,可进一步提高识别准确率。
3)将线多普勒和角多普勒彻底分离,有望获得更高的识别准确率。
