基于OpenFOAM的化学危害扩散预测求解器的开发与验证

韩朝帅， 诸雪征， 顾进， 张宏远， 张赫， 左钦文

(1.陆军防化学院， 北京 100000； 2.军事科学院 防化研究院， 北京 100000；3.陆军装备部项目管理中心， 北京 100000)

0 引言

化学危害扩散预测作为化学危害扩散模拟的关键基础，要将地形、障碍物、湍流等对危害扩散的扰动进行精细描述，以求精准可靠地预测未来时刻危害时空传输和扩散情况，是国家核生化安全和国防安全领域的重要基础性课题，对精确化提供防化保障辅助决策意义重大[1]。

化学危害扩散具有扩散尺度小、易受下垫面干扰，外部环境复杂、干扰因素多，数据来源杂、精度格式不一等特点，使得化学危害扩散预测的复杂性和不确定性大大增强。Scargiali等[2]采用计算流体力学软件CFX 4.4将重气扩散分解成污染物释放前的流场模拟、污染物释放时的扩散模拟两个步骤，开展了重气扩散精准预测研究。Henry等[3]利用大气模拟预测软件AERMOD模型对微粒污染的输运和扩散进行模拟分析，验证了大气扩散模型(AERMOD)在模拟面源排放颗粒物输运方面的预测能力。Vianello等[4]采用计算流体力学软件Fluent和工艺危险源分析软件(PHAST)开展城区氯气排放的数值模拟研究，分析了两种软件的适用性。

然而，目前化学危害扩散预测大多是通过商业软件来进行的，而现有商业软件中基本没有针对战场化学危害扩散模拟的功能，难以形成综合性的态势感知。在我国大力发展自主知识产权软件的大背景下，计算流体力学软件OpenFOAM的开源特性有助于打破软件的版权壁垒，自主地开发研究工具。Deng等[5]将内双迭代高效算法代替interFOAM求解器中的PIMPLE算法，构建适用于非稳态两相流问题求解的压力速度耦合求解器，并通过算例验证了所建算法的正确性、收敛性和有效性。曾剑锐等[6]通过热物性表制备与读取、原热物理派生类改写、热物性库编译3个步骤，构建了适用于超临界CO2流动与传热问题的sCO2FOAM求解器，该研究对于OpenFOAM求解器的移植性和拓展性编译的借鉴性较强。马宇等[7]针对中子输运模拟的复杂性和耦合性，基于OpenFOAM软件和有限体积法构建了中子输运动力学求解器ntkFOAM，实现了中子输运过程中传热传质的精细耦合计算。Abhishek等[8]将连续等离子体输运模型用于OpenFOAM软件开发平台，通过对几何体并行模拟、网格剖分、动量守恒模型进行设计编译，构建SOMAFOAM求解器，实现了低温等离子体在有限体积内的连续扩散模拟。

此外，化学危害扩散预测还包括信息融合、源项反演、数据同化等3项关键技术，通过OpenFOAM软件定制化开发化学危害扩散预测求解器，对于研究这3项技术具有很强的互通拓展性。陈存杨等[9]在压力- 隐式操作符分裂(PISO)FOAM求解器的基础上引入浓度标量场，开发用于重气扩散浓度预测的MyPISOFOAM求解器，但是其用于控制浓度标量场的微分方程未考虑沉降、多源效应，同时未植入相应的信息融合、源项反演、数据同化等算法，导致预测精度不高。因此，本文在PISOFOAM瞬态求解器[10]的基础上，将信息融合算法、四维变分同化算法(4DVAR)[11]、智能寻优算法植入OpenFOAM软件，详细研究化学危害扩散预测中基础参数和数据导入并实现智能更新的方法，构建用于化学危害扩散预测的求解器ChdpFOAM，同时对新开发的求解器进行应用验证，以确保不会因参数设置不当而导致预测失准。

1 ChdpFOAM求解器

1.1 ChdpFOAM求解器工作流程设计

PISOFOAM瞬态求解器中，PISO算法通过迭代求解离散化的动量预测方程和压力泊松方程，实现速度与压力的收敛耦合，进而构建扩散空间流场分布[12]。在PISOFOAM瞬态求解器的基础上，ChdpFOAM求解器综合化学危害扩散环境复杂、数据来源多维、边界条件多变的特点，嵌入信息融合模块、数据同化模块、源项反演模块，并通过智能寻优算法实现边界条件的智能更新和求解器的快速计算。ChdpFOAM求解器工作流程如图1所示。

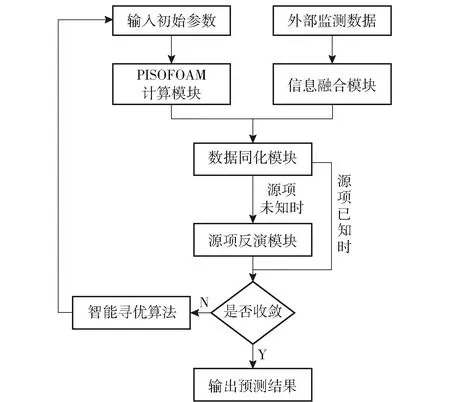
图1 ChdpFOAM求解器工作流程Fig.1 Flow chart of ChdpFOAM solver

由图1可知，在OpenFOAM软件中构建ChdpFOAM求解器的关键是如何将信息融合模块、数据同化模块、源项反演模块、智能寻优算法设计并编译至求解器中。因此，通过关键算法设计、基础参数和数据线索表的制备与读取、算法库和求解器的编译3个步骤，实现ChdpFOAM求解器的开发。

1.2 关键算法设计

1.2.1 信息融合算法设计

信息融合算法用于对外部监测数据进行处理和融合分析。针对外场环境面临化学危害浓度的差异性大、温湿度条件不可控等问题，采用联合分布函数对化学危害浓度和湿度进行漏警率影响分析，构建传感器漏警率与当前位置浓度、湿度的关系模型；根据环境中汽油、柴油、煤油等对报警装备的干扰影响，构建单个传感器虚警率模型；根据传感器分布规律，设计多个传感器分布式信息融合规则，构建基于贝叶斯的信息融合判决规则。信息融合模块中的模型算法已在文献[13-14]中详细介绍，最终的信息融合判决规则为

(1)

式中：k为地理网格坐标点的个数或监测节点个数；ui为单个监测节点的局部判决；PMi、PFi分别表示监测节点i的漏警和虚警概率，PMi=Pr(ui=0|H1)，PFi=Pr(ui=1|H0)；u0为融合后的判决；η为门限。当(1)式的左边大于等于右边时，融合输出u0=1，即认为H1成立，即危害事件成立，否则H0成立，即不存在危害事件。

1.2.2 数据同化算法设计

数据同化算法用于对产生化学危害浓度分布进行修正，其数据来源为信息融合模块(观测数据)和PISOFOAM计算模块(模拟数据)。相对于其他同化方法，4DVAR实现了整个同化时间窗口观测数据的同化，预测精度更高，适用范围更广，在解决化学危害扩散预测中具有明显的优势。本文采用4DVAR作为数据同化算法，构建适用于化学危害扩散的目标泛函梯度模型、数值预报模式及切线性算子。化学危害扩散目标泛函模型为

(2)

式中：C为扩散空间危害浓度分布；n为危害源数量；cj,0为第j个危害源初始时刻危害物浓度状态向量；cb为背景场向量；B为背景误差协方差矩阵；T为同化时间窗口；Ht为t时刻观测算子；cj,t为第j个危害源t时刻扩散浓度状态向量；yt为t时刻危害物浓度观测向量；R为观测误差协方差矩阵。

(3)

考虑化学危害扩散主要影响因素为对流项，为降低扩散预测误差，采用泰勒级数迎风差分构建各监测节点处的数值预报算子。t时刻监测节点(x,y,z)处的数值预报算子表达式为

(4)

根据t时刻各个监测节点的数值预报算子，即可得到t时刻整个状态向量的数值预报模式Mt=(M1,t,M2,t,…,Mk,t)。同理可得不同时刻的数值预报模式。假设t-1时刻各个监测节点的危害物预测浓度依次为ct-1=(c1,t-1,c2,t-1,…,ck,t-1)，根据切线性算子定义，得到t时刻数值预报切线性算子Dt：

(5)

1.2.3 源项反演算法设计

源项反演算法用于对真实源强与爆炸位置进行反向推演。通过以下3个步骤构建源项反演算法：1)根据等值线(面)梯度快速估算生成危害源位置的初始猜测，如图2所示；2)将初始猜测作为初始源项信息进行扩散模拟仿真，综合场景中不同位置布设的观测节点阵列的多组观测值进行数据同化；3)将同化后的预测数据与观测数据进行相对均方根误差(rRMSE)[15-16]计算分析，通过智能寻优算法实现循环迭代，最终获得rRMSE极小下的危害源位置和强度。图2中，A为梯度下降基准点，C、D、E为梯度下降中间节点，F为危害源位置初始猜测，B为A点等值线的极点。rRMSE计算模型为

(6)

图2 追踪格网数据估算等值线的梯度方向Fig.2 Gradient direction of contour line estimatedfrom tracking grid data

1.2.4 智能寻优算法设计

智能寻优算法用于对数据同化算法和源项反演算法进行快速求解最优值，以求得极小目标泛函梯度和最优源项信息。改进花朵授粉算法(IFPA)是Zhu等[17]提出的一种高效智能寻优算法，该算法将佳点集种群初始化、Deb可行性比较法、ε约束法融入花朵授粉算法(FPA)，全面提高了FPA的全局寻优能力和处理不同约束问题的灵活性。与此同时，相比于粒子群优化(PSO)算法、人工蜂群(ABC)算法、协同进化差分进化算法(CDEA)、遗传算法(GA)等方法，IFPA不受可行域不连通的限制，在求解过程中不需要目标函数的梯度或导数信息，为解决高维、多极值、不连续、不可微等复杂系统约束优化问题提供了新的思路和手段。因此，本文选取IFPA作为智能寻优算法。

1.3 求解器的编译

ChdpFOAM求解器的编译分为以下8个步骤：1)复制目录PISOFOAM到新的位置，新目录名为ChdpFOAM；2)将PISOFOAM.C改名为ChdpFOAM.C；3)删除依赖文件PISOFOAM.dep；4)修改编译文件files，进入Make目录，打开files文件，将EXE=$(FOAM_APPBIN)/ PISOFOAM改为EXE=$(FOAM_USER_APPBIN)/ChdpFOAM；5)删除原来的obj文件；6)在creatFiles.H文件中建立浓度场预测模型、信息融合算法、数据同化算法、源项反演算法、智能寻优算法；7)在ChdpFOAM.C中，通过fvScalarMatrix、fvVectorMatrix和.solve()工具加入浓度微分方程(CHEqn)、信息融合(u0Eqn)算法、数据同化(J4DEqn)算法、源项反演(rRMSEEqn)算法、智能寻优(CSEqn、QEqn)算法；8)编译wmake，实现算法模型间数据格式和接口设置。编译后的ChdpFOAM求解器计算过程如图3所示。

图3 ChdpFOAM求解器计算过程Fig.3 Calculation process of ChdpFOAM solver

2 ChdpFOAM求解器的适用性验证

以2018年福州大学某次六氟化硫(SF6)示踪实验为例，通过构建虚拟地理三维场景，对释放源信息、气象信息、扩散空间等进行设置或剖分，通过ChdpFOAM求解器对扩散过程进行模拟和求解。

2.1 SF6示踪实验基本情况介绍

2018年11月8日上午6时，在福州大学进行了大气扩散示踪实验，施放示踪物为SF6，风向为西北风，风速达中性稳定度，释放量为4.65 kg，释放时间为80 s。本次实验场地空间约为1.0 km×1.5 km，共设立2个固定气象站、7个便携式气象观测点和120个不规则取样点，以实时观测风速、温度、湿度、气压和示踪剂浓度等数据，释放点和监测节点布置如图4所示。

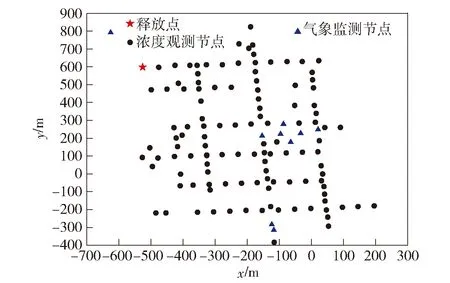
图4 实验点位布置Fig.4 Layout of experimental points

2.2 实验模拟与分析

2.2.1 实验参数设置

采用ChdpFOAM求解器对整个扩散过程进行模拟计算，空气设为主相，SF6作为第2相，各参数设置为：SF6密度6.52 kg/m3，动力黏度0.000 014 2 Pa·s。智能寻优算法中参数设置如下：种群规模N=200，授粉方式转换概率P=0.8，最大迭代次数T=500。

2.2.2 网格剖分及边界条件设定

通过blockMesh剖分、snappyHexMesh剖分和正交式非均匀交错网格剖分，对扩散空间中的释放源、下垫面和障碍物附近进行加密网格划分，如图5所示。图5中，扩散空间由x轴正向1 500 m、y轴正向1 000 m、z轴正向100 m的截取方式创建，网格分辨率设为10 m×10 m。

图5 扩散空间网格剖分Fig.5 Mesh generation of diffusion space

在网格剖分的基础上，对危害物的扩散初始边界条件进行设定：根据各气象观测点数据，构建扩散空间内初始风场信息，如图6所示。危害物释放点坐标为(-527 m，597 m)，释放高度为10 m，释放强度为58 g/s，释放持续时间为80 s；入口湍流强度为4.02%，入口面积为10 m×10 m，出口湍流强度为4.15%，外部气压为101 920 Pa，湿度24%。初始边界条件设定如表1所示。

表1 初始边界条件设定Tab.1 Initial boundary condition setting

2.2.3 实验过程模拟

在实验参数设置和计算仿真的基础上，对示踪剂在不同时刻、不同高度、不同剖面的浓度分布情况进行模拟和可视化展示。

2.2.3.1 不同时刻扩散过程模拟

图7所示为沿风向切面10 s、30 s、1 min、2 min、3 min、4 min时的示踪剂扩散浓度分布模拟状况。

图7 沿风向方向各时刻示踪剂扩散浓度分布效果Fig.7 Tracer diffusion concentration at each time along the wind direction

由图7可知，随着时间的增加，示踪剂沿风向方向逐渐蔓延至整个扩散空间；在遇到建筑物等干扰后，示踪剂会从两侧或上方随气流输送；在建筑物密集区域，示踪剂的扩散速度会减缓，部分地带出现滞留现象。

2.2.3.2 不同高度扩散模拟分析

以t=4 min为例，对示踪剂在不同高度h的空间分布状况进行模拟和分析，如图8所示。

图8 不同高度下示踪剂扩散浓度分布效果Fig.8 Tracer diffusion concentration distribution at different heights

由图8可知，2 m高度时，示踪剂扩散受地形、建筑物和树木的影响非常明显，部分区域示踪剂存在明显滞留现象，危害区域标识呈杂乱无序特征；随着高度的增加，地形和建筑物对示踪剂扩散的影响逐渐减小，危害区域也逐渐呈规则化特征。表明小尺度空间内危害物的扩散受下垫面影响明显，采用计算流体力学开展化学危害扩散预测优势十分突出。

2.2.3.3 不同剖面扩散模拟分析

以t=4 min为例，对示踪剂在平行于风向、平行于地面、垂直于风向等3种剖面下的空间分布状况进行模拟和分析，如图9所示。

图9 不同剖面下示踪剂扩散浓度分布效果Fig.9 Tracer diffusion concentration distribution in different sections

图10 4DVAR同化空间轨迹图Fig.10 4DVAR assimilation space trajectory

由图9(a)可知，沿着风向方向，随着扩散区域的增大，除部分建筑物密集区域外，其余区域示踪剂浓度呈逐渐降低态势。由图9(b)可知，同一高度下，示踪剂浓度分布主要受风向和下垫面作用。由图9(c)可知，同一区域内，不同高度的示踪剂浓度分布也相差较大，示踪剂的扩散不仅受下垫面影响，受风向风速和湍流的作用也十分明显。综合3个剖面可知，化学危害扩散预测不仅要按地域划分，更要按空间分层，对不同维度危害态势进行标注和显示。

2.2.4 ChdpFOAM求解器计算仿真

在实验参数设置基础上，按照ChdpFOAM求解器计算流程，对示踪剂扩散实验进行模拟仿真，求解经过数据同化和智能寻优后的流场和浓度场(源项已知)。由于释放量较小，持续时间较短，仅将4 min以内观测数据作为校验对象。图10所示为4DVAR同化空间轨迹图，图11所示为IFPA寻优变化曲线。

图11 IFPA寻优变化曲线Fig.11 IFPA optimization curve

由图10可知，4DVAR同化窗口基本覆盖整个搜索空间，可通过多组观测浓度场数据对预测浓度场数据进行同化处理，达到求解器同化目的；但是，受实验限制，观测浓度场数据较少，同化计算与真实环境下数据量和计算量均相差较大，算法的稳定性还需进一步进行验证。

由图11可知，5次寻优计算在迭代200～300次时均基本达到稳定收敛状态，J4DVAR(C)可逐渐降低至10%左右，说明IFPA的整体收敛性较强，预测结果基本满足现实需求，可通过减少迭代次数提高算法的计算速率。

2.3 实验结果分析

2.3.1 误差原因分析

由模拟实验可知，通过ChdpFOAM求解器可使J4DVAR(C)值降至10%左右，误差原因主要以下3个方面：

1)寻优算法计算误差。IFPA只能通过循环迭代求得相对最优值，很难类似穷举法得到最优值。此类误差可通过多次独立仿真进行降低，但是不可能避免的。通过对上述实验进行20次独立实验，最终J4DVAR(C)最小值为9.54%。

2)观测仪器测量误差。示踪剂取样设备、气象测量设备、示踪剂分析设备等测量偏差也是导致计算误差产生的原因。为此，对0.522 μg/m3浓度的SF6进行了7次分析，相对标准偏差为4.1%，如表2所示。

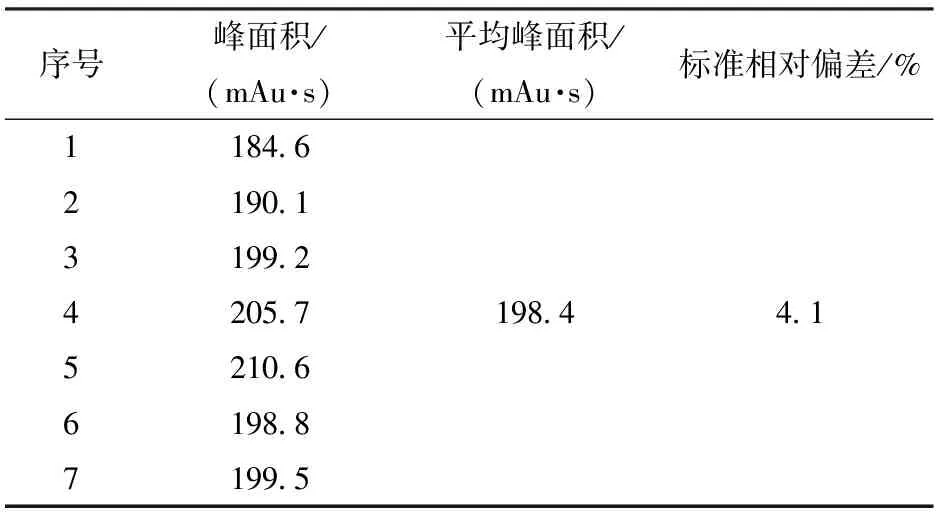
表2 SF6分析相对标准偏差Tab.2 Relative standard deviation of SF6 analysis

3)背景场误差。造成实验预测模拟误差的另一个重要原因是背景场误差，主要由下垫面干扰误差和风场误差构成。下垫面干扰误差与地理模型精细程度、气流与建筑物的干涉等息息相关。风场误差主要由监测节点的数量和布局不够系统均匀造成。

2.3.2 ChdpFOAM求解器优劣性分析

为验证ChdpFOAM求解器优劣性，按照均匀分布、覆盖面全的规则选取10个监测节点，以90 s、120 s、180 s、240 s 4个时刻数据作为分析数据，分别通过ChdpFOAM求解器和PISOFOAM求解器计算求解，分析二者与真实观测值之间的差异性，结果如表3所示。各监测节点坐标依次为：(-420 m，570 m)、(-170 m，600 m)、(-190 m，820 m)、(-340 m，410 m)、(-320 m，100 m)、(-400 m，450 m)、(-330 m，260 m)、(-360 m，-60 m)、(-330 m，130 m)、(-350 m，-210 m)。浓度差异计算表达式为

(7)

式中：d1为ChdpFOAM求解器模拟预测浓度值与真实观测浓度值的差异；cC为ChdpFOAM求解器模拟预测浓度值；cT为真实观测浓度值；d2为PISOFOAM求解器模拟预测浓度值与真实观测浓度值的差异；cp为PISOFOAM求解器模拟预测浓度值；d3为ChdpFOAM求解器相对PISOFOAM求解器模拟精度提高程度。通过数据分析，将ChdpFOAM、PISOFOAM求解器扩散模拟与真实观测结果进行对比分析，如图12和图13所示。

由表3和图12、图13可知：d1最小值(4.71%)出现在6号监测节点(120 s)，最大值(34.73%)出现在8号监测节点(240 s)，平均误差百分比为12.98%；d2最小值(7.76%)出现在10号监测节点(180 s)，最大值(33.98%)出现在5号监测节点(180 s)，平均误差百分比为18.95%；d3最小值(-0.20%)和最大值(16.43%)均出现在240 s时刻(1号、3号监测节点)，平均误差差异为5.97%。从模拟结果角度分析，在下垫面相对平坦、建筑物少的区域(6号监测节点、10号监测节点)，ChdpFOAM和PISOFOAM求解器计算误差均较低；在距建筑物相对密集的区域(8号监测节点、5号监测节点)，ChdpFOAM和PISOFOAM求解器计算误差均较高；相比于PISOFOAM求解器，ChdpFOAM求解器的计算精度总体提升6%左右；180 s内ChdpFOAM求解器计算精度明显高于PISOFOAM求解器，但是240 s时刻同化效果比较微弱。

表3 ChdpFOAM、PISOFOAM求解器扩散模拟与真实观测结果对比Tab.3 Comparison of the simulated diffusion results ChdpFOAM and PISOFOAM solvers and the real observed results

图12 ChdpFOAM、PISOFOAM求解器扩散模拟与真实观测数据分析Fig.12 Analysis of the simulated diffusion data of ChdpFOAM and PISOFOAM solvers and the true observed data

图13 ChdpFOAM和PISOFOAM求解器预测误差分析Fig.13 Prediction error analysis between ChdpFOAM and PISOFOAM

为进一步分析植入模块后对求解器计算效率的影响，分别对不同迭代次数、不同时间步长下ChdpFOAM和PISOFOAM求解器需要的计算时间进行统计分析，如表4所示，其中d4表示ChdpFOAM和PISOFOAM求解器的耗时比。

表4 ChdpFOAM和PISOFOAM求解器不同步长模拟时间消耗统计Tab.4 Time consumption statistics of ChdpFOAM andPISOFOAM solvers at different step sizes

由表4可见：以模拟240 s扩散为前提，使用ChdpFOAM和PISOFOAM求解器对不同时间步长时的扩散进行模拟，时间步长越短、迭代次数越多，二者的耗时越长；以30 s步长为例，采用PISOFOAM求解器耗时729 s，采用ChdpFOAM求解器耗时967 s， PISOFOAM求解器的计算效率相对更高；从耗时比角度分析，ChdpFOAM求解器与PISOFOAM求解器的平均耗时比为1.33，计算效率下降了约32.57%。说明信息融合、数据同化、智能优化等模块的运行，未对求解器计算效率造成明显下降，基本满足实际需求。

3 结论

本文针对化学危害扩散受地形、障碍物、湍流等影响显著的特点，基于OpenFOAM软件开发平台设计适用于化学危害扩散预测的ChdpFOAM求解器，并对其适用性进行实验验证。通过实验验证分析，得到如下主要结论：

1)小尺度空间内，危害物的扩散受下垫面作用明显，ChdpFOAM求解器具有较强的实用性。在下垫面相对平坦、建筑物少的区域，干扰因素较少，ChdpFOAM求解器的预测误差相对较低；在建筑物密集区域，SF6的扩散速度会减缓，部分地带出现滞留现象，ChdpFOAM求解器的求解难度大大增加，可能导致预测精度的降低。

2)沿风向方向，由于SF6的密度约为空气的5倍，易受沉降效应聚集形成近地面毒剂云团；远离释放点位置，经过建筑物和下垫面的湍流扰动，部分SF6会发生抬升导致浓度下降，经过建筑物后又逐渐向近地面沉降。

3)相对于PISOFOAM求解器，ChdpFOAM求解器在计算精度约提升6%，求解精度改进效果明显。

4)相对于PISOFOAM求解器，ChdpFOAM求解器计算效率下降约32.57%，下一步可通过模块优化和内部接口设计提升计算效率。