基于CFD的双道超车过程气动特性分析

唐洪涛，杨峻程，张 祥，刘学龙

（1.天津科技大学机械工程学院，天津 300222；2.中汽研（天津）汽车工程研究院有限公司，天津 300300）

双道超车会对主超车及被超车产生连续干扰，破坏单车流场，对汽车的操纵稳定性和行驶稳定性产生较大影响。由ABDEL进行的风洞试验结果表明，在选取的11个纵向位置的水平截面上，压力分布存在明显变化，阐明了道路车辆行驶时的相互气动干扰。HOWELL等在对轿车与卡车模型进行的试验中发现，超车过程卡车周围的压力场，特别是卡车前部，所呈现出的负荷响应更为显著。针对车辆相对位置这方面的研究，HOMOUD等通过Solid Works Flow得到4个超车位置的流场压强和速度变化，并发现轿车在完成变道时出现最大阻力系数，但试验选取位置较少，对超车的连续性变化规律研究存在局限性。NOGER等则通过试验发现不同横向间距和纵向间距对超车过程的气动力和力矩产生明显影响，但试验模型过于简化，对试验精度会产生一定影响。张世村在对两个Ahmed模型进行仿真时发现，随着横向距离的变小，两车之间的相互响应变大，相应的阻力系数就会变大。而吴允柱等则利用Ahmed模型探究了车速对超车过程的影响，研究表明，相对速度对主超车的影响较小，对被超车的影响较大，相同相对速度下，绝对速度较低的两辆车存在更大的瞬态气动响应。邵南在进行超车过程的气动特性研究时，引入了涡的概念，并提出边缘旋转圆柱法对尾部涡流进行优化，阐述了涡流对超车过程的影响，对提高车辆气动性能具有重要意义。

基于以上研究，本文对双道超车过程中的流场变化做出分析，研究超车过程中压力场、速度场以及涡的变化对各车辆的气动力及风压中心的影响，并分析不同车速在超车过程中对气动力的影响，最后据研究结果给出相应结论。

1 基本控制方程组

依据《道路交通安全法》第78条规定，道路行驶车辆最高车速不得超过120 km/h。本文选用汽车的最大行驶速度约为108 km/h，马赫数约为0.088，小于0.4，可认为该风速范围内为不可压缩流体，所以密度为常数，适用质量守恒方程为：

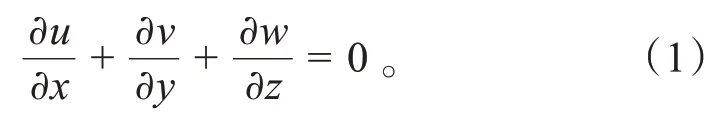
动量守恒方程为：

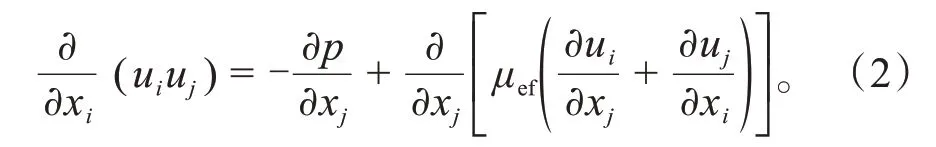
能量守恒方程为：

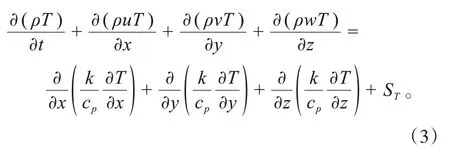
式中：、和分别为速度矢量在、和方向上的分量；为流体微元上的压力；为湍流粘性系数；为时间；S为流体的内热源及由于粘性作用流体机械能转换为热能的部分；为流体力学传热系数；c为比热容；为温度。

在汽车空气动力学中，通常用气动力系数来描述汽车的空气动力学特性。式（4）为侧向力系数计算公式。

式中：为车身所受侧向力；v为合成气流相对速度；为汽车正投影面积。

2 数值模拟

2.1 模型选取和计算域的确定

模拟选用某款SUV，原车尺寸为：长4 629 mm，宽1 898 mm，高1 655 mm，轴距约2.8 m。汽车质量约1.8 t，正投影面积约2.7 m。按原车尺寸简化为矩形，长用表示，宽用表示。车头与车尾按照比例做圆角处理。为确保超车过程中车辆周围的流场不受计算域的影响，将计算域长度设为40，宽设为20。各方案提前行驶一段距离再进入数据采集区域，保证气体的充分流动。计算域和超车模型如图1所示。

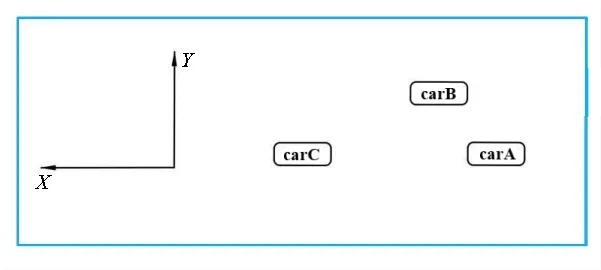
图1 汽车模型和计算域

2.2 网格划分

模拟采用三角形非结构化网格，车身网格尺寸设定为0.1，计算域网格尺寸设定为0.6，目的是保证车身周围网格密集些，远离车身的网格疏松些，提高模拟过程车身周围流场的精度。图2为计算域网格模型，网格数约158 000个。

图2 网格模型

2.3 计算域的设定

计算域右侧为压力进口，左侧为压力出口。求解器选用transient（瞬态求解器），计算采用-epsilon湍流模型，动网格参数选择Smoothing（网格光顺）和Remeshing（网格重划分），Spring Constant Factor（弹性因子）设置为0.05。采用动网格进行数值模拟，当车辆发生位移时，需要对网格重新划分，目的是为了保证较好的网格质量。

2.4 双道超车方案

3车均从右侧向左行驶，carA为主超车，carB和carC为被超车，且速度相同，所有方案车辆间距一致。carB在主超车右前方，carC在主超车正前方，记carA的中心与carB的中心沿轴正方向的距离为，沿轴正方向的距离为。超车方案见表1。

表1 超车方案

3 仿真结果分析

3.1 压力云图分析

以case2为例进行压力云图分析，时间步长为0.000 5 s，时间步数为10 000步，每隔25个时间步采集一张图片。并以行驶方向为正方向，规定carB在carA右侧，carC在carA左侧。图中单位为Pa。

图3 b、图3a的放大图，carA超越carB半个车身。通过观察放大图标记区域，carA右侧存在一个压强分布变化明显的区域，两车之间压强由高压向低压过度，使carA右侧车身受力不均。同时carA车头左侧与车尾右侧的低压区会加剧carA车身的扭转趋势，该位置carA车身存在逆时针横摆力矩，有使carA绕垂直轴转动的趋势。carB也存在同向扭转趋势，引起carB车身横摆角发生改变，影响carB的行驶稳定性和驾驶安全。

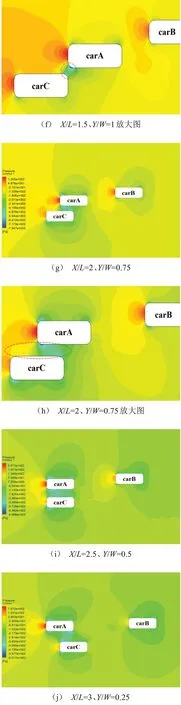
图3 双道超车压力云图

carA车头的正压区已经干涉carC车身右侧压强场，使carC右侧压强略高于左侧，carC车身受力发生变化。

在超车过程中，该位置主超车carA与被超车carB存在同向扭转趋势，容易发生碰撞，存在一定危险性。

如图3c、图3d所示，carA右侧受到carB前端正压区影响，与carA左侧形成较大压强差，使carA车身两侧受力不平衡，对carA的行驶稳定性造成影响。通过观察放大图的标记部分，carA车头左侧和carA尾部与carB车头之间均存在负压区，使carA车身存在逆时针扭转趋势，仍存在与carB剐蹭的风险。

随着车辆相对位置的变化，carB与carA之间的负压区减小，carB左侧正压区增大，车身两侧压强差逐渐减小。

carA车头正压区开始干涉carC右侧压强场，导致carC右侧压强偏高，车身两侧压强差变大，使carC车身受力增大。但carA距离carC车尾仍有半个车身，所以两车出现碰撞的概率较小。

如图3e、图3f所示，此时carA车头与carC车尾接近。carA右侧压强高于左侧，放大图标记处的小面积负压区会使carA车头两侧压强差增大，carA行驶变得不稳定，carA车头存在向carC扭转趋势，对carA变道形成阻碍作用。

carC受carA正压区影响，右侧车身周围呈现大面积正压区，与左侧的负压形成较大压强差，对carC的行驶稳定性带来不利因素。加之车尾负压区的共同作用，使carC存在逆时针扭转趋势，可能引起carC车身偏离正常行驶轨迹，存在与carA车头相撞的风险。

carB两侧压强差逐渐减小，但车身左侧仍然受到carA尾流影响行，两侧仍存在压强差，车身受力仍存在不平衡。

如图3g、图3h所示，carA追上carC半个车身，carA与carC之间出现负压区。放大图标记处能够看出carC右侧前车身呈正压区，后车身呈负压区，使carC右侧车身受力不均，高压区将carC车头向左侧推，低压将carC车尾向右侧吸引，carC车身存在逆时针扭转趋势，产生影响carC直线行驶的横摆角，carC存在跑偏现象。

由于两车之间的负压区，carA前车身两侧存在明显压强差，使carA车头有向carC扭转的趋势，对carA变道形成阻碍作用。当两车间距较近时仍存在剐蹭风险。

此时carA尾流对carB左侧流场干扰已经很小，carB基本恢复单车行驶状态。

如图3i所示，carA与carC车头平齐。两车之间存在负压区，carC受负压区影响车身会产生被吸近carA的趋势。而carA此时仍然处于变道过程，为远离carC的状态，因此发生碰撞的概率较低。

如图3j、图3k所示，主超车carA在方向逐渐远离carC，两车之间的气流干涉逐渐减弱。carA完全超过carC时，超车过程结束。

3.2 速度矢量图分析

以case2的速度矢量图进行分析，图中单位为m/s。

图4a为/=0.5时的速度矢量图，此时carA右侧气流与carB左侧气流相互干涉，两车之间形成一个流向复杂、流速较低的气流干涉区，通过放大图4b可知，由于carA右侧与carB车头气流干涉，形成三向气流相互冲击现象，明显降低了该处气流速度，而carA左侧此时存在紧贴车身且尺寸较大的涡结构，导致carA前车身两侧受力不平衡。carA后车身与carB前车身之间形成的狭窄区域使流入该区域的气流流速明显变快，导致该处两车车身相互吸引。该时刻carA两侧空气流动状态不平衡，对carA超车过程的稳定性造成影响。

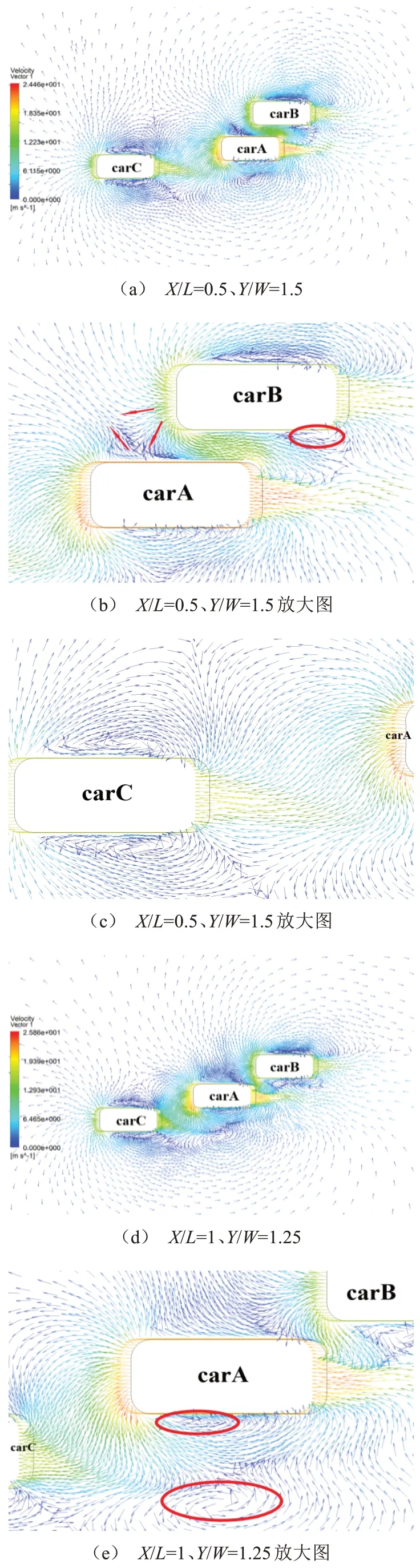
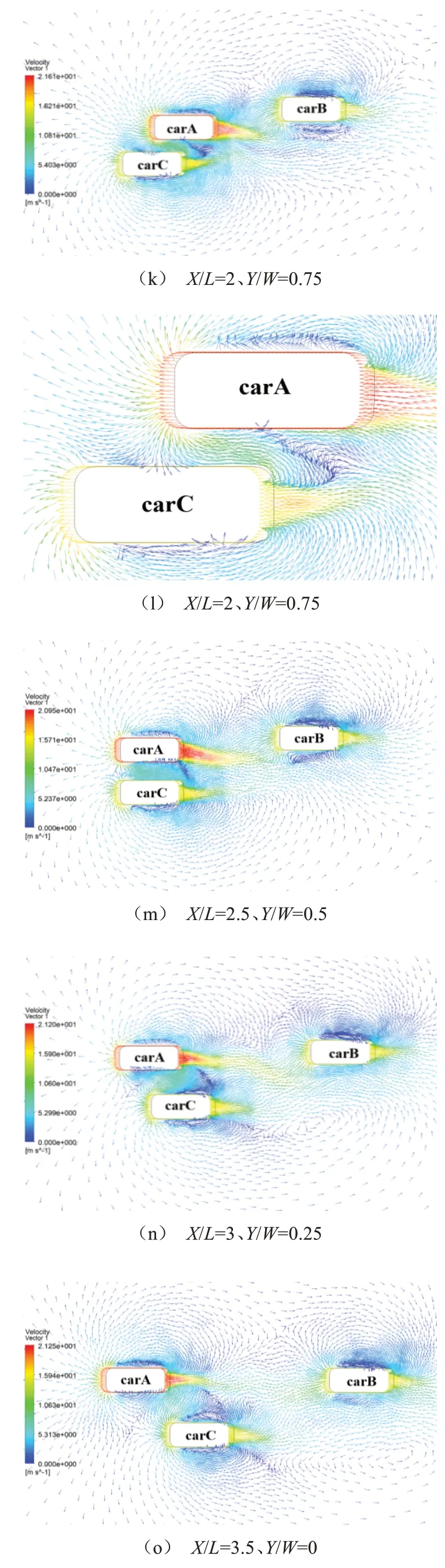
图4 速度矢量图

从图4b中可以观察到，carA和carB之间流出的气流速度逐渐降低，一部分在carB尾部形成涡流，一部分与carA尾流融合，而此时carB右侧存在尺寸较大的涡结构，与carB左侧小涡为非对称状态，导致carB两侧空气流动状态差异明显，行驶变得不稳定。carA和carB此时存在剐蹭风险。

随着carA、carC在方向上的接近，carC右侧气流开始受到carA前端气流影响，如图4c所示，此时carC右侧涡的涡心偏移，涡形状由扁变圆，两侧涡变得不对称，carC车身受力发生变化。

如图4d为/=1时的速度矢量图，carA完全超越carB。由放大图4e可知，carA右侧气流与carB车头气流相互干涉，形成低速流区，且此时carA左侧有两个较大涡流，紧贴车身的涡呈扁平状，尺寸较小，而远一些的涡呈椭圆形，尺寸较大。此时carA车身两侧空气流动状态相差明显，carA车身两侧形成较大压力差，给carA变道带来不利因素。

如图4f所示，随着carA在方向上与carB的距离拉开，两车之间的快速气流区域迅速减小，同时carB左侧涡的涡心前移，两侧涡形态仍存在明显差异，车身仍会受到两侧气流状态不平衡而产生的压力差。

随着carA与carC在方向上靠近，如图4g所示，carA前端气流加强对carC车身右侧气流干涉，carC车身右侧涡的涡心继续前移，涡形态由扁变圆，两侧涡形态变的不对称，两侧气流状态失去平衡，使carC受力发生变化。

如图4h所示，carA车头与carC车尾平齐，由于carA车头气流的强烈干扰，此时carC右侧涡消失。如图4i所示，carC右侧气流呈低速流动状态，而此时carC左侧存在尺寸较大且紧贴车身的涡，导致carC车身两侧气流流动状态产生较大差异，carC两侧受力不平衡，行驶状态变得不稳定，可能产生横摆角，影响其直线行驶。

而此时carA右侧出现紧贴车身的强制涡流，如图4j所示，carA前端气流一部分冲击在carC车身，一部分从两车之间流向后方，在carA左侧形成涡结构，该涡尺寸较小，且涡心靠前，与carA右侧涡形态差异明显，使carA两侧受力不平衡。

同时carB左侧受到carA尾流的干扰继续减小，carB逐渐恢复单车行驶状态。

如图4k所示，carA追上carC半个车身，而carA与carB在方向上已经存在一定距离，对carB的气动干扰逐渐减小，carB车身受力逐渐减小，基本恢复稳定行驶状态。

如图4l所示，carA前端流向两侧的气流冲击carC车身，流速降低，carA和carC之间的狭窄区域使流经空气速度加快，导致两车相互吸引。流经两车之间的气流一部分合入carC尾流，一部分与carA后方的反向流相互冲击，使流速迅速降低。该时刻carA与carC之间形成一个空气流速变化复杂的区域，使两车行驶的稳定性受到影响，产生横摆角，增大两车剐蹭风险。

如果产生的横摆力矩具有减小横摆角的作用，那么汽车具有稳定的气动特性。

如图4m所示，carA车头与carC平齐，两车之间空气流速明显大于两侧，仍存在相互吸引趋势，而carB前端气流对carA尾流造成一定干扰，使carA尾流向左侧偏移，但随着carA、carC在方向上距离的拉开，危险系数大大降低。

如图4n、图4o所示，随着carA变道的完成，carA与carB在方向上的距离和carA与carC在方向的距离均已拉开。3车之间的气动干扰逐步减弱，最后3车恢复单车行驶状态。

3.3 流线图分析

湍流的一种特征就是旋涡，即流体中存在着的局部迅速旋转的流体微元，并且这些流体微元处于不断的形成、变化与被破坏过程中，并在此动态过程中消耗流场能量，使流场中的车身受力变得复杂多变，给车辆行驶稳定性带来影响。

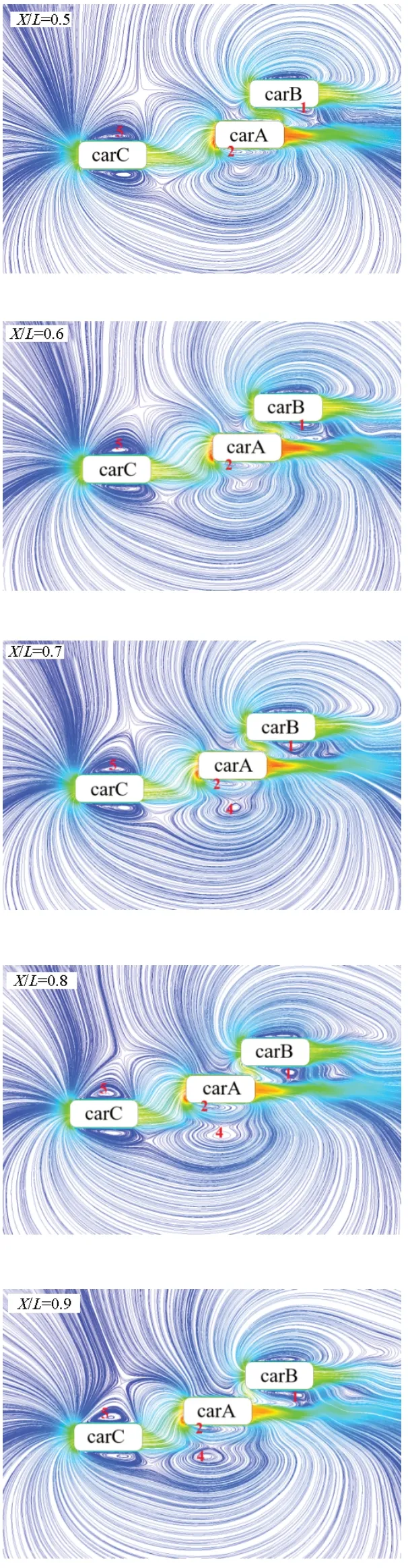
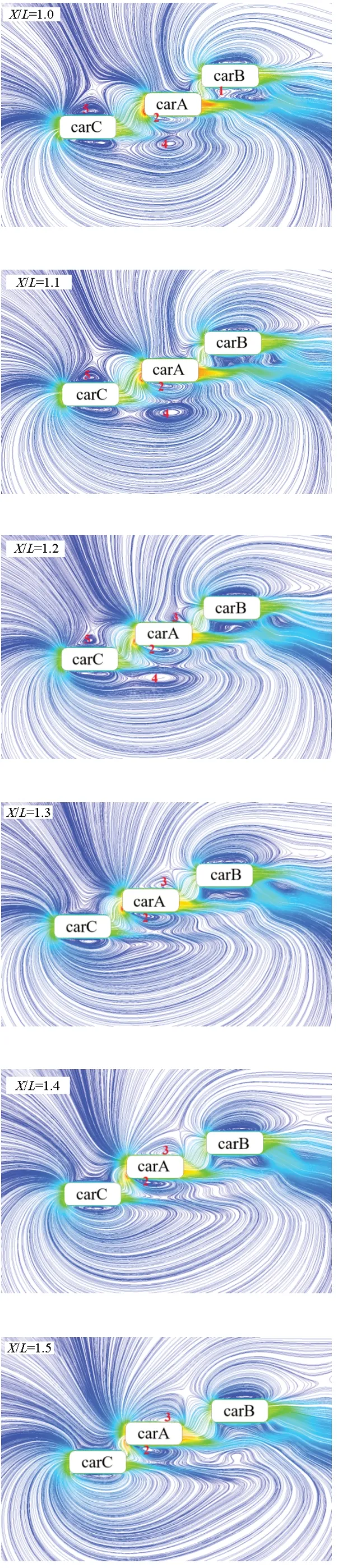
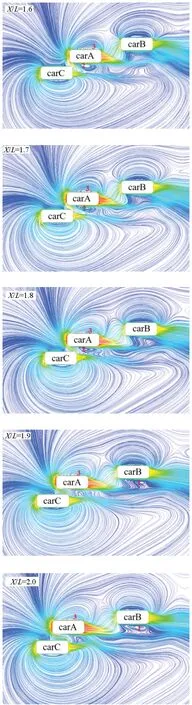
图5 速度流线图

在/=0.5时，carB内侧存在1涡，该涡为紧贴车身的强制涡。由于主超车此时与carB较近，其尾流对carB内侧流场产生干涉，使1涡受到carA尾流的挤压，形状呈扁椭圆形，且尺寸较小。carB两侧涡形态此时很不对称。随着carA对carB的超越，1涡的涡心向前移动，尺寸逐渐变大，/=1.1时，1涡消失。1涡在超车过程中经历形状、尺寸的变化，从形成到消失消耗流场能量，使carB的受力一直在变化。/=1.9时，主超车与carB已存在一定距离，1涡再次出现，carA的尾流对1涡影响越来越小，直至干涉消失，1涡回归正常形态。

在/=0.5到/=2.0的过程中，carB左侧涡的变化很活跃，是carB侧向力变化的原因之一。

carA在超车时，车身两侧流场存在明显变化。随着车辆相对位置的变化，carA车身两侧的强制涡，2涡和3涡，也随之变化。2涡受carC尾流影响，形状较扁。carA运动至/=1.6时，2涡的涡心向车身后方移动，且形状从扁逐渐变圆。/=1.9时，2涡消失。

3涡在/=1.2时出现，此时3涡尺寸较小，位于carA车身后部。随着carA与carB的距离拉开，3涡尺寸逐渐变大。涡心向前移动，逐渐回归正常形态。

在/=0.7时，carA外侧约2 m处出现一个自由涡，4涡，该涡尺寸较大。随着车辆的运动，4涡尺寸继续变大。在/=1.3时，4涡消失。自由涡的涡心压强较小，会对carA产生吸引力。

主超车carA周围的大涡在/=0.5至/=2.0变化较为活跃，使其车身受力变化较为频繁，是此过程carA车身侧向力产生波动的重要因素之一。

在主超车carA不断向carC靠近的过程中，对carC车身内侧流场影响越来越大。/=0.5时，carA距离carC在方向上为5 m远，此时carC两侧涡形态正常。随着carA的靠近，观察到carC内侧的5涡有“起鼓”的现象，逐渐由紧贴车身的扁涡变成椭圆形涡。在/=1.3时，5涡消失。

在carA不断接近carC的过程中，随着5涡的消失，carC内侧压强将逐渐变大，使carC侧向力发生较大幅度变化，可能导致carC在行驶时出现偏离正常行驶轨迹的现象，对驾驶产生负面影响。

综上所述，双道超车过程中，车辆相对位置的变化将对车身周围涡产生较大影响，从而影响车辆稳定性，给车辆行驶带来不利因素。所以，超车时涡的研究对驾驶安全具有重要意义。

3.4 侧向力分析

双道超车时，汽车的相对位置发生变化，侧向力随之改变。在特殊超车位置会使主超车和被超车的侧向力产生较大波动，给车辆稳定性和驾驶安全带来不利因素。文中提及的侧向力均为垂直车身的力。

如图6所示，carA侧向力在/=0.5至/=2.5过程中变化幅度很大。在/=1.0附近出现最大值。在/=1.0至/=2.0的过程中，主超车位于两辆被超车之间，此区间流场变化相对复杂，使carA的侧向力出现较为频繁的波动，给超车过程的稳定性带来不利影响。

图6 三车侧向力系数C s变化图

carB的最大侧向力出现在/=0.5附近，此时的carB有被吸近主超车的趋势，该位置属超车过程的高危位置。随着carA完成对carB的超越，carB受力急剧变化。在/=1附近，carB侧向力出现了方向改变。当carA逐渐远离carB后，carB受力逐渐恢复稳定。

随着主超车的靠近，carC侧向力逐渐增大。在/=1.75附近出现最大值。此时carA的车头距离carC车尾较近，但随着主超车在方向上对carC的超越，两车方向上距离越来越远，carC侧向力在达到最大值后开始减小，在/=2.5附近，carC车身受力方向改变。当carA完成超车时，carC侧向力最终趋于平稳。

双道超车使3辆车的气动力产生强烈变化，且主超车在两车之间时出现更为强烈的力的波动，所以，在进行双道超车时，主超车在两车之间时的危险性是非常高的。

3.5 风压中心数据分析

双道超车时，由于车辆之间的气动干涉的随机性，车身气动力等效作用点会发生位置变化，即汽车风压中心位置的变化，影响车辆行驶的稳定性。以case3为例，图中正值代表风压中心相对质心前移，负值则反之，对超车过程的风压中心变化进行分析。

如图7为3辆车行驶过程的风压中心变化图。在超车过程中，/=0至/=0.5，carA风压中心由质心后移到质心之前，且位移量较大，给carA变道超车带来不利因素。在/=0.5、/=1和/=1.5时，carA压力中心向前偏移量较大，且/=2时出现最大向前偏移距离，对carA的行驶稳定性造成一定影响。/=3时，carA压力中再次移向质心之后，而风压中心的位置变化会对carA的变道行驶带来一定干扰。

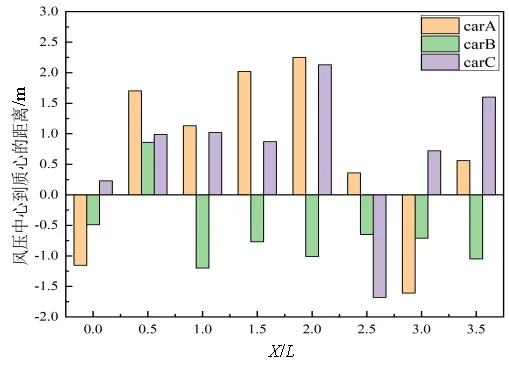
图7 三辆车风压中心位置变化

超车过程中，carB压力中心在/=1时出现最大后移，其位置变化影响carB的行驶稳定性。/=0.5时出现carB在行驶过程中唯一风压中心前移，/=0.5至/=1过程中，carB风压中心位移量较大，使该过程carB受力点变化较大。

由于carA的靠近而产生的气动干扰，在/=2时carC风压中心出现最大位移，对其行驶稳定性造成一定影响，在/=2.5时，风压中心后移，所以在/=2至/=2.5过程中，carC风压中心从质心前移动到质心后，且位移量较大，使此过程carC的受力点位置变化幅度较大，对carC的行驶稳定性造成一定影响。

表3为3车不同时刻的风压中心位置、侧向力及力矩方向变化情况。可以看出，从/=0到=3，carA车身均存在逆时针横摆力矩，在/=1和/=1.5时，carA风压中心位移和侧向力较大，产生较大横摆力矩，且在/=1附近，横摆力矩达到最大值，表明/=1附近存在carA超车过程最不稳定的位置，变道方向与力矩方向相反，容易引起车身振动，影响超车过程的稳定性。

表3 不同位置车辆横摆力矩方向

carB在行驶过程中，/=0时车身存在顺时针横摆力矩，而/=0.5至/=3.5均为逆时针横摆力矩，在/=0.5附近carB所受横摆力矩达到最大值，表明当carA超越carB半个车身时，会使carB产生较大逆时针扭转趋势，影响carB直线行驶的稳定性，该位置为carB行驶过程中最不稳定的位置。

carC在/=0至/=2.5行驶过程中，车身存在逆时针横摆力矩，而/=3至/=3.5，车身则受到顺时针横摆力矩影响。/=1.5和/=2时，carC车身横摆力矩较大，在/=1.5附近，carC所受横摆力矩达到最大值，即carA车头接近carC车尾时，carC出现较大逆时针扭转趋势。此时刻为carC行驶过程最不稳定的位置。

4 不同车速对超车过程的影响

4.1 压力云图对比分析

根据上文侧向力变化趋势，分别选取carA，carB和carC的最大侧向力位置压力云图进行分析。

由图8a、图8b对比发现，30 m/s时的carA车身右侧呈现更高的压强，且高压区域面积更大，而车身左侧同时出现更低的负压，且负压区更大，即30 m/s时的carA相比于20 m/s时的carA车身两侧出现更大的压强差。表明速度越大，此时carA车身两侧压强差越大，对超车越不利。不同车速时carA车头左侧与车尾右侧均呈现出负压区，且速度较大的carA呈现出更为明显的负压区，说明速度较大时，将使carA车头产生更强烈的扭转趋势，对变道过程的稳定性产生更多影响。

/=0.5附近出现carB的最大侧向力，通过图8c、图8d的比较，发现速度的增大，使carA与carB之间出现压强更低的低压区。主要表现为车速越快，压强越低，低压区面积越大。表明随着车速的增大，两车之间压强变低，carB扭转趋势越强烈，使carB更大几率会出现逆时针横摆角，影响carB直线行驶的稳定性，更容易发生两车相撞的风险。

且25 m/s时的carB前端呈现更高的压强，高压区面积更大，使carA前车身两侧产生更大压强差，加强carA在变道行驶时的扭转趋势，使超车过程的危险性提升。

由图8e、图8f对比可知，carA速度增大，车头正压区面积和压强明显增大，使carC车身右侧压强明显增大，同时，车速的增大使carC车尾右侧与carA车头左侧之间的低压区压强降低，面积增大。速度的增大使carC车身两侧产生更大的压强差，车身承受更大气动力带来的负荷，增大了carC偏离直线行驶的风险。

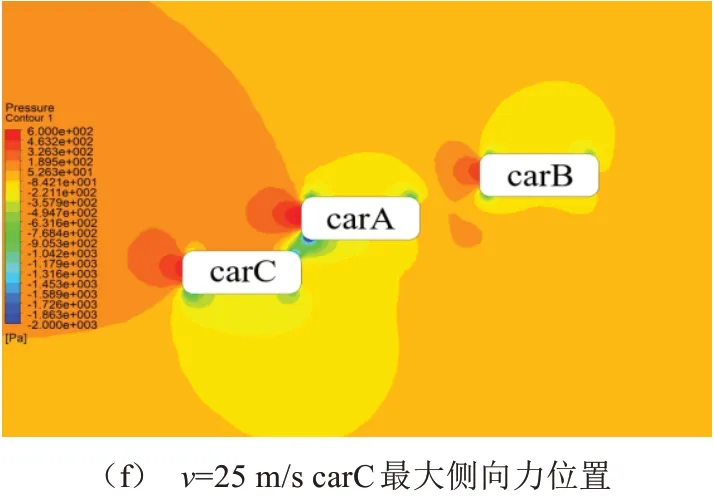
图8 三辆车最大受力位置压力云图

4.2 最大侧向力分析

如图9所示，随着车速的增长，主超车和被超车的最大侧向力近似线性增长。从4个工况中比较主超车carA的最大侧向力发现，case1比case2增长约74.2%，比case3增长约146.7%，比case4增长约215.4%。比较carB发现，case1比case2增长近72.6%，比case3增长近175.7%，比case4增长近315.2%。再比较carC，case1比case2增长近41.7%，比case3增长近105.8%，比case4增长近202.0%。

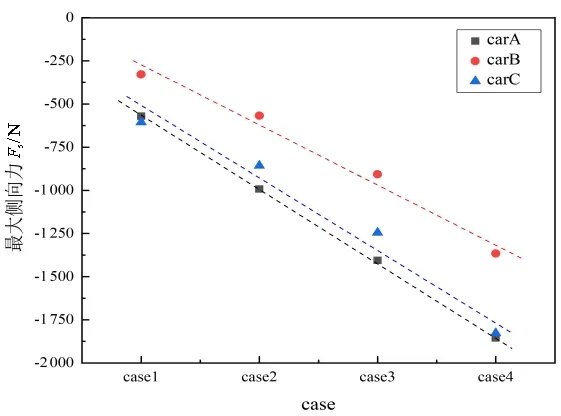
图9 不同绝对车速最大侧向力变化图

综上所述，在双道超车过程中，车速的提高对被超车carB的影响最为明显，其次是主超车carA，影响较小的是被超车carC。但从变化图中可以看出，被超车carC在相同速度超车过程中的侧向力是大于被超车carB的，所以3辆车经过最大受力位置时，行驶稳定性均会受到较大影响。

5 结论

（1）双道超车过程中3辆车周围的压力场、速度矢量场和涡量场发生剧烈变化，且主超车在两辆被超车之间时流场变化更为剧烈，对汽车行驶稳定性和操纵稳定性带来负面影响。

（2）双道超车过程，随着主超车相对位置的变化，使3车周围涡形态发生复杂变化，涡的变化是车辆气动力变化的重要原因之一。

（3）车辆行驶时，侧向力是影响行驶稳定性的重要因素。在双道超车过程中，随着车辆相对位置的变化，/=0.5附近出现carB最大侧向力，/=1.0附近出现carA最大侧向力，/=1.75附近出现carC最大侧向力值。

（4）通过对3辆车各位置的横摆力矩进行分析，carA在/=1附近横摆力矩达到最大值；carB在/=0.5附近达到最大值；carC在/=1.5附近达到最大值，即这3个位置分别为carA、carB和carC行驶过程中最不稳定的位置。

（5）随着绝对速度的增加，主超车与被超车所受最大侧向力呈线性增长。车速的提升对被超车carB的影响最为明显，其次是主超车carA，影响较小的是被超车carC。