基于形状特征的导航信道群时延约束分析
2022-06-10倪少杰王峰毅李蓬蓬肖志斌
倪少杰,王峰毅,李蓬蓬,肖志斌,张 可
(国防科技大学 电子科学学院, 长沙 410000)
0 引言
全球卫星导航系统(global navigation satellite system, GNSS)可以通过卫星向用户提供全天候、连续、实时和高精度的定位、导航及授时服务。其信道模型对预测和评估 GNSS的性能以及改进接收信号处理算法设计是极其重要的。其中接收信道为卫星导航系统完成高精度定位授时、星地时间同步、卫星精密定轨等重要系统业务提供重要支撑,是保障导航系统服务性能的基础。接收信道中,射频前端的非理想群时延特性会影响导航系统的定位性能。当相频响应呈线性关系时,群时延特性为一个常数。它对于测距的影响只有一个延时。当相频响应不是线性关系时,群时延特性成为一个变量,它对测距的随机误差和系统误差将产生一定的影响。
对于高精度导航系统而言,接收信道的伪距测量精度会对后端的钟差解算精度产生影响,从而影响授时精度,因此需要根据实际需求对接收信道的伪距测量精度进行约束。为了在此约束条件下,更加直观地指导接收信道射频前端的设计,为高精度导航信道模拟提供支撑,需要探究射频前端非理想群时延特性对高精度导航系统的测距性能影响,并对其指标进行约束分析。
由于导航信道群时延的非理想特性,其信号自相关函数的相关峰会发生畸变,由此会引入时延估计偏差,一般用于评估导航系统的测距定位性能。时延估计偏差一般采用较为成熟的早迟码估计器进行估计,在实际工程中一般采用非相干的形式。
利用非相干早迟码估计器,很多学者关于群时延特性对导航系统测距性能的影响做了相关研究。文献[9]选取椭圆滤波器进行建模,得到了全球定位系统(global positioning system, GPS)信号和伽利略卫星导航系统(Galileo navigation satellite system, Galileo)信号经过固定参数的椭圆滤波器后,在不同相关器间隔和不同信号功率情况下的时延变化情况,文献[10]在此基础上,继续研究了以巴特沃兹和切比雪夫滤波器群时延建模情况下的时延变化情况,但这些研究都没有对群时延参数进行改变,并探究其对导航系统的时延影响规律。文献[4]设计并分析了线性和抛物线群时延滤波器对时延估计的影响,并得到线性群时延相比于抛物线群时延对时延估计影响更大的结论,但是其群时延特性没有以实测群时延数据为参考进行设计,只得到理论的仿真结果,无法指导实际射频前端设计。文献[11]分析了低通滤波器群时延特性的波动幅度和不同的波动形状特性对测距系统误差的影响,但是对于群时延特性的波动形状特性的分析没有得到规律性结论。文献[12-15]对相频曲线进行泰勒展开,对零阶、线性和抛物线群时延产生的测距误差影响进行了定量研究,但是其参数没有实际物理意义,无法反映出群时延特性具体特征。文献[6,16]利用三角函数和抛物线函数对群时延特性进行建模,得到了三角函数频率幅度以及抛物线幅度等参数对时延估计误差的影响,但是其数据为理想的对称仿真数据,而实际的滤波器群时延特性并不呈现上述规律性特征。综上所述,传统群时延模型无法对群时延特性的具体特征进行描述,其参数不具有实际物理意义。基于上述分析,本文根据射频前端滤波器群时延特性实测结果,提取群时延形状特征参数,提出了基于分段抛物线的导航信道群时延分析模型。利用非相干早迟码估计器分析群时延形状特征参数对导航系统测距性能的影响,并得到给定时延估计误差指标下的形状特征约束结果。
1 传统群时延分析模型
群时延特性对于接收机的影响主要体现在波动特性,即相对群时延特性。利用矢量网络分析仪测量出某型号射频前端腔体滤波器的相对群时延特性如图1所示。
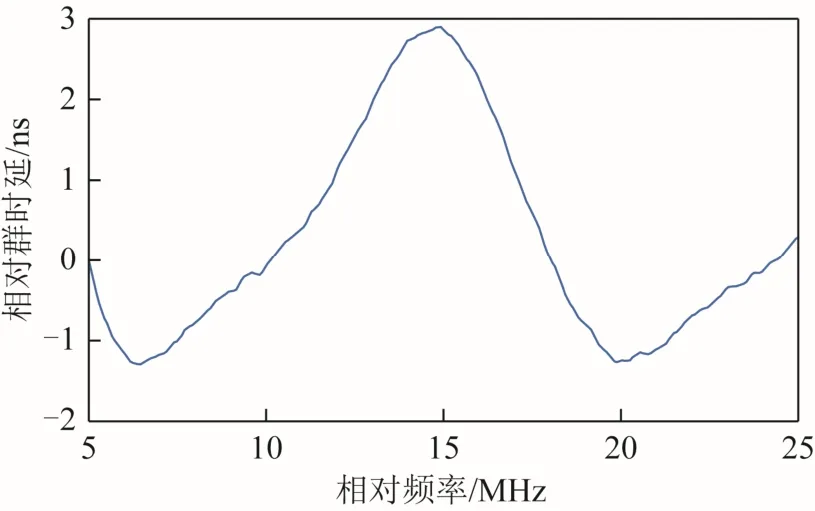
图1 相对群时延特性
传统的群时延分析模型包括线性模型、抛物线模型和三角函数模型等,根据图1所示的相对群时延特性,对于窄带系统而言,在不同的带宽条件下,可以用不同的相对群时延分析模型表示,如图2所示。
通过图2分析可知,传统的群时延分析模型适用于带宽较窄且形状较为规则的情况。对于矢量网络分析仪测量的多组同型号射频前端腔体滤波器相对群时延特性,可以分析总结出以下规律:

图2 不同带宽下的相对群时延分析模型
1)相对群时延特性在通带范围内呈波动特性,在通带范围内有至少一个极大值和极小值;
2)各极值的绝对值一般不同;
3)各极值部分所占带宽一般不同。
线性模型和抛物线模型无法准确描述群时延通带范围内的多个极值特性,三角函数模型无法体现极值绝对值以及所占带宽不同的特点。
有学者将群时延特性进行泰勒展开或者傅里叶展开进行分析,泰勒展开表达式为
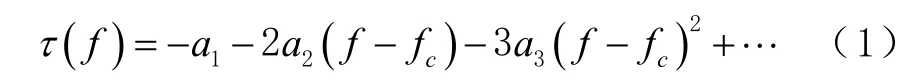
式中:()为群时延特性;为频率,其取值范围为通带频率范围;f为中心频点;,=1,2,3,…为泰勒展开系数。
傅里叶分解展开表达式为

式中:为带宽;为常数项系数;c和s为非常数项傅里叶系数。但是看出泰勒展开和傅里叶展开只能对给定的群时延特性进行分析,其参数无法描述群时延的具体特征,无法依据分解展开系数对实际群时延特性进行有意义的分析。
针对上述传统群时延分析模型的局限性,需要建立新的群时延分析模型。
2 基于形状特征的相对群时延分析模型
针对传统群时延分析模型无法对射频前端相对群时延模型准确分析的问题,本文提出了基于形状特征的相对群时延分析模型,根据上一节得到的实测数据规律分析,提取相对群时延特性形状特征,并根据形状特征提出能够准确分析相对群时延特性的分析模型。
由图1可以得出,该相对群时延特性在通带范围内存在 2个极小值和 1个极大值,其极值点分布情况为实测结果中最为普遍的情况,可以作为该型号腔体滤波器的通用极值点分布情况,并在此条件下提取波动幅度、极值不一致性和占空比不一致性等相对群时延特性形状特征。
为了对相对群时延建立数学模型,需要对其形状特征进行约束并规定其具体表现形式,其详细描述总结如表1所示。

表1 相对群时延特性形状特征详细描述总结
假设相对群时延特性在通带边缘处的相对群时延值为0,则利用起始点和结束点以及极值间的零点可以将通带分为极小值部分和极大值部分。极小值部分即为包含相对群时延极小值的相邻零点之间部分,极大值同理。根据表1所提出的形状特征及其具体表现形式,本文提出以各极值部分为分段的分段抛物线相对群时延分析模型。
对于左右两端零点分别为f和f,段内极值点为的分段相对群时延,则段内抛物线模型为

通带内相对群时延特性共有3个分段,假设第 1个极小值部分、极大值部分和第 2个极小值部分的分段编号分别为1、2、3。若第1个极小值数值为,其余分段极值与第 1个极小值的比值分别为、。按照分段编号顺序,极值部分的占空比为,,,其占空比应满足++=1。
对于通带带宽为(单位为MHz)的带通滤波器,其相对频率范围为0~,则各分段参数如表2所示。

表2 分段参数
基于以上分析,通带内相对群时延特性分段抛物线模型的数学表达式为

为了方便后续仿真分析,在此规定相同类型的极值部分占空比相同为先验条件,即

由此将表1中形状特征的详细描述转化为模型参数表示,结果如表3所示。

表3 相对群时延特性形状特征总结的模型参数表示结果
以上述分析为基础,可以以形状特征的具体表现形式为变量,仿真分析形状特征对时延估计误差的影响。
3 仿真原理
仿真流程图如图3所示。

图3 仿真流程
本文采用自主生成二相移相键控(binary phase shift keying, BPSK)信号,根据通带中心频率和带宽要求设计带通滤波器,将BPSK信号通过带通滤波器后下变频至中频,剥离载波至基带信号。将基带信号送入非相干早迟码估计器中进行时延估计。其中带通滤波器的幅频特性为理想幅频特性。
以上一节分析得到的形状特征的模型参数表现形式为变量,设计生成通带内相对群时延特性。
根据相对群时延分段抛物线模型的数学表达式,推导得出通带范围内的相频特性表达式为

由于相位函数为连续函数,根据分段处函数相等可以得出

式中:为相位;为常数项,可设为0。
因此可以得到通带范围内的相频特性。根据幅频特性和相频特性则可以设计出给定群时延的带通滤波器。
利用早迟码估计器得到的码片偏移量将偏移后的伪码与输入信号进行相关累加得到伪码信号的归一化自相关函数,如图4所示。

图4 非理想自相关函数
根据归一化自相关函数,对于给定的早迟相关间隔,可以得到更精确的码片偏移量,使得(−/2)=(+/2),由此可以得到对应的时延估计误差τ为

根据上述分析,可建立形状特征的模型参数对时延估计误差的影响分析平台。
4 仿真结果与实测分析
依据于上一节搭建的影响分析平台,本节以表3中表示形状特征表现形式的模型参数为变量,在规定的相应前提条件下进行仿真,并分析得出基于物理可实现的形状特征对τ的影响结果,最后在给定时延估计偏差约束条件下对相对群时延形状特征约束条件进行分析。
为了使仿真参数变化范围满足物理可实现的约束范围,在此默认仿真参数变化范围为
1)第一个极小值数值为不超过4 ns;

3)各分段占空比不少于0.1。
当所有的极大值与极小值绝对值都相同时,在以3-1表示的不同占空比差异下,波动幅度对时延估计误差的影响如图5、图6所示。
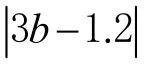
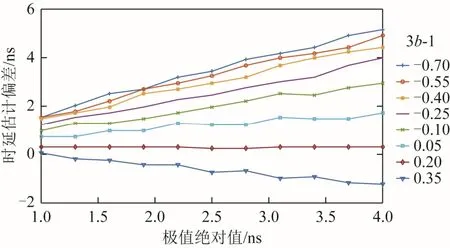
图5 不同占空比差异下,波动幅度对时延估计误差的影响
当占空比无差异时,在不同极小值的情况下,极值不一致性对时延估计误差的影响如图6所示。

图6 不同极小值的情况下,极值不一致性对时延估计误差的影响

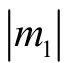
从图6中可以得出以下结论:
1)当占空比与极值间比例固定时,时延估计偏差的绝对值与波动幅度呈正相关;
2)当占空比与波动幅度固定时,时延估计偏差会随极大值的增大而增大,随第 2个极小值的增大而减小。
以基于卫星双向比对的钟差测量不确定度2 ns为时延估计偏差约束条件,在不改变仿真参数设置的前提下,对图5、图6中的仿真结果设置阈值,得到在物理可实现前提下,占空比不一致性与波动幅度的约束关系以及极值不一致性与波动幅度的约束关系如图7所示。

图7 形状特征之间的约束关系
图7(a)至图7(c)的仿真参数设置分别与图5、图6(a)、图6(b)相对应。根据图7所得到的形状特征约束关系,可以为高精度导航接收信道射频前端滤波器设计提供形状特征约束指标,从而保证高精度卫星双向比对钟差计算结果,实现精准授时。
实测实验利用矢量网络分析仪测量多组接收机的射频前端模块群时延特性,通过信号源产生 B3I信号,测量相对应的定位误差,测量时长为1 000 s。群时延特性及相对应的定位误差如图8所示。

图8 群时延特性与对应定位误差实测结果

图8(a)为测量得到的近似于规则波动的群时延特性;图8(b)为对应的定位误差,其均值为9.021 2 m;如图8(c)所示的群时延特性测量结果相比于图8(a),其波动幅度相对增大;图8(d)为对应的定位误差,其均值为10.131 1 m;图8(e)所示的群时延特性测量结果相比于图8(a)存在极值不一致性;图8(f)为对应的定位误差,其均值为 15.351 6 m,因此波动幅度增大会引起定位误差的增大;图8(g)所示的群时延特性测量结果相比于图8(a)存在占空比不一致性;图8(h)为对应的定位误差,其均值为12.021 6 m。
通过上述 4组具有不同形状特征的群时延特性及其对应的定位误差测量结果,可以得出波动幅度、极值不一致和占空比不一致等形状特征对高精度接收机定位误差会产生影响,从而证明了基于分段抛物线的相对群时延分析模型从形状特征的角度对群时延特性进行分析具有实际意义,其研究结果对于高精度导航接收信道射频前端滤波器的设计优化具有一定的指导意义。
5 结束语
本文以某型号射频腔体滤波器的相对群时延特性实测数据为参考,以 2个极小值和 1个极大值的极值点分布情况代表该型号腔体滤波器的通用极值点分布,并提取基于物理可实现的波动幅度、极值点不一致性和占空比不一致性等群时延形状特征。
建立基于分段抛物线的相对群时延分析模型,相比于传统群时延分析模型,更准确地体现相对群时延形状特征。利用早迟码估计器探究相对群时延形状特征对时延估计误差的影响并得到以下结论:
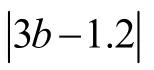
2)在占空比无差异的情况下,当极值间比例固定时,时延估计偏差的绝对值与波动幅度呈正相关。
3)在占空比无差异的情况下,当波动幅度固定时,时延估计偏差会随单个极大值的增大而增大,随第2个极小值的增大而减小。
以卫星双向比对钟差测量精度为时延估计误差约束指标设置阈值,获得群时延特性形状特征之间的具体约束关系。最后利用多组监测接收机实测数据,证明了基于分段抛物线的相对群时延分析模型良好的分析效能,对高精度导航接收信道射频前端滤波器的设计具有一定的指导意义。
