电力现货市场出清价格预测误差风险分析

赵越，刘思捷，白杨，高海翔，龚超，蔡秋娜，王子石，龚昭宇

(1.广东电网有限责任公司电力调度控制中心，广州510060；2. 广东电网有限责任公司市场安全经济运行与市场化调度重点实验室，广州510230；3. 北京清能互联科技有限公司，北京100084)

0 引言

放松管制、引入竞争已成为电力市场建设的重要任务，目前国内8个现货试点均已进入结算试运行阶段[1 - 2]，形成具有时间及空间特性的现货市场出清价格。准确的出清价格预测对系统运营商及市场主体具有重要意义[3]，系统运营商需要通过预测价格对市场风险进行预警及预控，发电厂、售电公司则需要通过预测价格评估交易风险、制定竞价策略。

现有的现货价格预测方法主要可分为数据驱动和模拟出清两类[4]。数据驱动即挖掘出清价格与自身及其他相关因素规律，并使用统计学习、人工智能等方法建立并拟合回归模型。文献[5]将外生变量引入自回归模型，使传统时间序列模型可考虑其他相关因素影响；文献[6]使用随机森林模型预测现货出清价格，并形成一套科学的输入特征筛选和模型调参方法；文献[7]分析了高比例风电下影响电价的主要因素，使用长短期记忆网络(long short term memory，LSTM)算法构建电价预测模型。数据驱动方法在风电[8]、气象[9]及负荷预测[10 - 11]等领域也应用广泛，具有较强的通用性。然而，不同于上述领域，现货出清价格具有明确的计算模型(安全约束经济调度，security constrained economic dispatch，SCED)，模拟出清法即通过模拟该计算模型间接得到出清价格。文献[12]通过预测负荷、发电、边界条件等信息，基于SCED模型和多参数规划得到节点电价和线路阻塞的概率预测结果。

无论是对预测方法本身的改进还是评价能否实际应用，均需要基于对预测误差的评估。现有文献中的价格点预测评估指标与其他预测领域相同，都是基于时段平均与绝对值的准则，如绝对值误差(absolute error, AE)、平均绝对值误差(mean absolute error, MAE)[13]、平均绝对值百分比误差(mean absolute percentage error, MAPE)[14]、均方根误差(root mean square error, RMSE)[15]等，认为预测效果可以随上述指标的减小而改善。

然而传统指标应用于价格预测误差分析，存在以下不足：1)系统运营商、发电商、售电商等主体预测价格用途不同，传统指标没有基于特定用途分析误差影响；2)不同主体在各时段交易电量不同，采用平均准则无法衡量不同时段预测误差带来的经济风险；3)若出现传统指标在模型间各有优劣的情况，将导致预测模型难以选择。

相比传统评估指标，风险评估指标可以考虑在工程应用中由误差导致的实际后果。如文献[16]提出了风电功率预测误差的风险评估指标，其认为风电功率预测正误差与负误差对系统可靠性影响不同，误差绝对值与经济性影响也不同，故采用预测事件概率与事件发生损失的积分作为模型评价指标。文献[17]提出使用负荷预测误差对系统机组组合成本的影响作为负荷预测模型评价依据。文献[18]分析了电价预测误差对市场参与者的经济影响。但目前仍未有在电价预测领域统一建模、针对不同决策主体分别考量其风险的分析方法。

综上，本文提出价格预测误差风险评估指标，该指标考虑了市场主体因价格预测误差产生的不同经济后果，针对主体各时段交易电量赋予不同权重，可以准确反映风险成本。本文所提指标综合衡量不同决策主体因预测误差带来风险，可以给予各类市场主体可靠的模型评估及选择参考。

1 预测误差评估指标分析

本节对预测领域常用的误差分析指标进行梳理和对比，并对其进行总结并分析其不足后，归纳出一般化的指标设计原则。在此基础上，提出一般化误差评估指标模型。

1.1 常用预测误差评估指标

为具体说明，本文例举4种常见的点预测误差评估指标，具体如下。

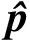
(1)

然而现实预测任务大多数需要评估多时段的预测结果，绝对值误差指标不具备数据降维能力，因此不适用于多时段场景。

2)平均绝对值误差(EMAE)。通过在EAE基础上取误差序列的平均值，可得到EMAE指标。

(2)

式中T为时段数。EMAE适用于多时段场景，因具有计算简单、含义明确等特点已在预测任务中广泛使用。但其衡量标准基于待预测量真值，难以直接对比模型在不同任务中的预测效果。

3)平均绝对值百分比误差(EMAPE)。通过对每一个误差值除以其真值并记百分比，可得到EMAPE。

(3)

相比绝对值指标，EMAPE对误差比例有更直观认识，可以衡量一个模型在不同任务中的预测效果。但当真值序列接近0时该指标存在数值问题[19]。

4)均方根误差(ERMSE)。ERMSE引入非线性变换计算序列相似度。

(4)

相比其他使用1范数损失处理正负误差的指标，在ERMSE中，2范数损失通过平方运算放大了预测值与真值之间的距离，且具有可微、可导的性质。

此外针对不同预测场景，一些学者也使用了季节性平均绝对标准误差(seasonal mean absolute scaled error, SMASE)、均方差标准误差(root mean square scaled error, RMSSE)等作为模型评估依据[20]。

1.2 预测误差评估指标设计原则

图1展示了在两时段预测任务中预测误差与4种常见指标的关系。本节以此为例总结在设计误差评估指标时，除唯一性与单调性以外，仍需要考虑的几个因素。

图1 常见误差评估指标几何表示Fig.1 Geometric representation of common error assessment indicators

2)多样本权重：在多样本任务中，衡量样本集内各子样本量化到指标中的标准是否一致。EMAE、ERMSE即假设子样本无差异，EMAPE根据样本真值设置权重，一些综合评价指标也会根据日类型(工作日、节假日)设置权重，以凸显任务偏好。若多样本权重不同，图1曲面在x轴与y轴投影具有不同形状，如图1(c)EMAPE。

3)误差值非线性程度：反映指标值随误差值改变而改变的程度。若存在常数C，使dφ/de=C， 则称误差值为线性的。ERMSE通过对误差序列平方和开根引入一定非线性，可使指标对单个误差较大值更为敏感，在图1(d)中误差与指标值的关系也从线性条件下的平面变为曲面。

1.3 一般化误差评估指标模型

综合1.2节评估指标设计原则，提出针对时间序列点预测的一般化误差评估指标如式(5)所示。

(5)

式中：kt为t时刻正负误差权重，其取值如式(6)所示；et为t时刻预测误差；wt为t时刻的样本权重；m为误差非线性系数；α(·)为指标激活函数。

(6)

式中：kt+、kt-分别为t时刻的正误差权重值、负误差权重值。

样本权重主要衡量不同时段预测误差的影响，如对需求侧用户可以使用预测用电量作为权重系数，在用电量低的时段，预测偏差对决策及成本影响较小，因此误差权重较低；在用电量高的时段，较小的预测偏差即可能对其购电决策及最终成本带来较大影响。非线性系数主要影响较大预测误差的敏感程度，若单位预测偏差对市场主体错误决策导致的收益损失呈线性关系，则该项取1；若小范围的误差对决策影响不大，而较大误差会导致更大损失，此时即可取2以上的非线性系数。激活函数用以控制指标的值域取值大致范围，一般有开根、除以序列数等操作。

设计指标时可根据具体应用场景将一般化误差评估指标中的参数/激活函数设置为固定值/确定函数。可以看出1.1节所列几种常用指标均为一般指标参数及激活函数取值不同时的简化形式。下一节将讨论针对现货出清价格预测任务，各决策主体应如何根据自身需求选取指标参数。

2 现货出清价格预测误差风险评估指标

从不同主体预测电价的动机不同、传统指标难以有效反映购电成本两方面举例说明风险评估指标存在的必要性，并分别从运营商和不同市场主体的预测电价使用场景及决策思路阐述指标设计思路并给出指标数学模型，最后总结上述风险指标的共性特点。

2.1 风险评估指标的必要性

现货市场交易会产生日前电价与实时电价，日前电价用以结算日前交易竞价空间内未被中长期合约覆盖的电量，实时电价则用以结算实际用电量与日前中标电量的偏差部分。对系统运营商而言，预测出清价格可以作为事前风险评估体系的一部分，用以判断系统是否存在高峰价格风险及分析潜在的市场力被动用的可能性，在该场景下不需要关心价格在正常范围内存在的预测误差；对发电商而言，预测现货出清价格可以作为其对中长期合约的价格锚定，也可作为日前申报时的决策依据，而就评价预测模型而言，发电商更关心预测误差对其实际收益产生的影响；而对售电商，在采用用户侧报量不报价及统一结算点电价结算的模式下[21]，售电商博弈空间在通过预测日前与实时价格高低确定其申报策略，因此更关心日前及实时预测结果是否会改变其申报倾向；用户则更在意预测误差是否会改变其用电计划进而是否影响购电总成本。

另一方面，在市场主体充分博弈的市场中，现货价格难以准确预测，各类预测模型由于数学机理不同可能产生不同的误差分布，此时依据传统指标评估结果选出的“最佳模型”未必对所有决策主体都是最佳的。文献[18]采用某工业用户购电成本与MAPE误差评估指标的关系形象说明该问题：如图2所示，虚线表示将该用户42天内的电价预测误差MAPE值由高到低排列，柱形表示用户当天实际购电成本比理想购电成本高出的比例。可以发现更低的MAPE指标并不一定能带来购电成本的降低。

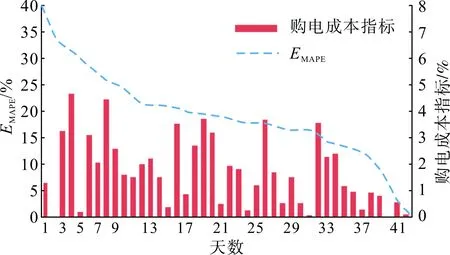
图2 购电成本与MAPE值关系示意Fig.2 Relationship of electricity cost and MAPE value

因此，对于价格预测不同的使用场景，更应该关注预测误差对市场风险、主体利益的影响，从而设计更符合决策主体需求的误差评估指标，而本文认为的风险指某事件发生导致结果偏离预期的程度。

2.2 系统运营商指标设计

考虑系统运营商预测出清价格作为其事前风险评估体系的一部分[22]，需要重点关注以下3种情况：1)交易电量大；2)结算价格高；3)预测误差大。交易电量大意味着相同数值的价格预测误差对系统总成本的影响更大，因此指标应更关注预测模型在交易电量大时段的准确性；结算价格高是指事前风险预警体系中的一项重要内容为高价预警，而同样的预测误差发生在高价时段的负面影响显然就高过低价时段，因此指标对高价时段的敏感度应低于低价时段；预测误差大是指相比于多个时段的小误差，一个时段的大误差更容易对主体释放错误的市场信号，因此在误差之和相等的情况下，指标应更关注少量单个误差值更大的情况。

考虑上述因素，在设计运营商误差评估指标时，通过以下方法将上述3点因素计入指标：1)在样本权重中加入市场化交易电量，提高高交易电量时段样本的权重；2)在样本权重中计入价格真值，提高高价时段样本的权重；3)对各时段误差值引入2阶非线性系数，提高高误差时段误差值对指标的影响。所设计系统运营商指标φISO如式(7)所示。

(7)

wex,t=λ(pt)·λ(dt)

(8)

式中：wex,t为t时刻的运营商样本权重；dt为t时段内市场化交易电量；函数λ(x)表示对x在样本集X内进行min-max归一化。

(9)

此外，开根号无实际物理涵义，一般是存在取平方操作时为避免指标数值过大的配套数值处理方法，本文设计指标沿用该处理方法。

2.3 发电商指标设计

若不考虑发电商在现货市场中的投标策略及其对出清价格的影响，仅从事后角度评价电价预测误差对发电商收益的影响，可发现单位预测误差的收益影响与发电商在该时段的结算电量有关，故在评价发电商使用的电价预测模型时，可引入以预测价格结算的电量作为样本权重，使指标值反映模型因预测不准对发电商预期收益造成的偏差。发电商误差风险指标如式(10)所示。

(10)

式中：k为正负误差权重，取k+=k-=1；样本权重wgen,t设置为以该价格结算的电量，如预测日前电价时使用日前中标电量，预测实时电价时使用实时偏差电量。

该指标适用于以报量报价方式直接参与电能量市场并采用分时结算机制的发电机组，若机组暂未直接参与市场或以自调度方式参与市场，则其没有预测现货出清价格并参与博弈的需求。

2.4 售电商指标设计

在国内现货试点实践中，考虑到需求侧相对成熟性及抗风险能力较弱，多采用报量不报价、用户统一结算电价的方式(广东、山西和山东均采用该方式)，此时售电商在参与现货市场博弈时主要根据日前与实时价差改变申报策略，如预测实时电价高于日前电价，则在日前多申报电量，在实时市场售出套利。

因此，可将售电商的这种博弈特性引入对预测模型的性能评价指标中，在评估日前电价预测模型时可采用实时价格作为标尺设置样本权重，仅将预测误差可能导致售电商申报方向错误从而产生亏损的部分计入指标，定义售电商误差风险指标为：

(11)

式中：k为正负误差权重，取k+=k-=1；样本权重wseller,t取值如式(12)所示。

(12)

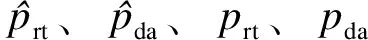
售电商指标φseller主要关注预测误差是否会改变其利用日前与实时电价价差套利的申报策略，若预测误差对其申报策略不会产生影响，则售电商对该误差关注度较低；若会产生影响，则将其反映至风险指标中。

2.5 需求侧用户指标设计

考虑在需求侧报量不报价及统一结算点电价结算的模式下，需求侧用户作为价格接受者，日前申报决策模型为：

(13)

式中：b为所有时刻负荷申报量集合；bt为t时刻负荷申报量；ζ为相关约束条件。该模型目的为通过改变申报量使预期购电成本最低。用户实际购电成本为。

(14)

若能获得完全准确的电价预测结果，可获得用户理想购电成本：

(15)

进而，将理想购电成本与实际购电成本的差值称为价格预测误差成本。

cerror=cactual-cideal

(16)

注意到误差成本本身即可作为预测模型评估指标，但具有建模复杂、需要求解优化等缺点，本文对该指标进行一定简化，在事后评估阶段采用实际负荷申报量替代式(15)中的准确电价申报量，使需求侧用户误差风险指标可以近似价格预测误差成本。

(17)

式中wbid,t为t时刻的实际负荷申报量。需求侧用户指标φuser反映预测误差对用户实际购电成本产生的影响，一定程度上能反映数值误差背后的经济特性，相比传统指标更具现实意义。

此外，按照2.1节所述存在常规价格预测误差指标的减小不一定使主体收益提高(如图2所示)的情况，发电商或售电商均可使用价格预测误差成本作为模型评估指标，考虑到发电商及售电商决策模型相对复杂，本文直接阐述其指标设计思路和使用场景。

2.6 误差风险评估指标特点

在现货市场环境下出清电价具有较高不确定性，准确预测十分困难，而不同电价预测方法由于模型及数据层面的局限性，总会存在不同的误差分布特性，预测指标的价值在于将上述高维的误差分布映射至一维，从而使用户能对比不同模型性能、选取最佳模型进行使用。然而，传统预测指标仅考虑了误差值的部分“数值特性”，没有考虑不同用户的实际用途差异及对应的“经济特性”，使用传统预测指标可能无法有效选取最佳模型。基于该问题，本文对误差数值特性及其背后意义进行归纳总结，并分别针对系统运营商、发电商、售电商和需求侧用户在预测现货出清价格时的不同目的，设计了不同的误差分析指标，所提指标相比传统指标具有如下优势。

1)针对各主体不同交易行为设计指标数学模型，运营商、发电商、售电商等主体可根据预测价格用途的不同选取指标参数；

2)指标根据各时段交易电量设计不同权重，可以准确考量交易电量较高时段更大的经济风险，同时使指标能考虑误差的经济特性；

3)指标确定后评价结果具有唯一性，不会出现多个传统指标共同评估时可能出现的结果矛盾。

3 算例分析

本节中，3.1节说明算例概况、电价预测模型及预测结果，3.2节分析传统评估指标评估结果及其不足，3.3—3.4节分别从指标数值一致性、对各主体不同需求的可定制性和对用户实际决策收益的提高3个方面论述本文所设计指标的有效性。

3.1 算例说明

本文以广东现货市场2020年8月连续结算试运行电价数据为基础，预测统一结算点日前价格，其余使用到的电价采用真实值，并以某电厂、某售电公司中标电量作为评价依据，最后建立工业用户购电决策模型，验证本文所提风险评估指标的有效性。本文算例中，电价预测部分基于Python及Tensorflow实现，优化问题部分基于Yalmip建模并调用Cplex求解。采用某电厂所接220 kV母线作为发电侧结算节点，统一结算点作为用户侧结算节点，结算周期为1 h，统一结算点电价曲线见附录图A1。可以看到日前电价序列呈现一定的日、周周期性，价格整体水平与实时电价较为契合，但部分时段实时电价会出现日前电价没有的价格尖峰。

算例将对比4种常见的电价点预测方法(M1—M4)的误差指标，具体如下。

1)M1：相似日法[23]。周二—周五使用前一日价格作为预测值，周六—次周一使用上周同日价格作为预测值。

2)M2：SARIMA时间序列预测模型，对各时刻单独建模，共24个模型，模型参数由AIC准则[24]确定。

3)M3：ANN神经网络，使用前两日48个时刻价格作为输入，预测日24个时刻价格作为输出。网络有50节点隐藏层，采用ReLu激活函数和sgd优化器，迭代200次。

4)M4：LSTM神经网络，使用前23个时刻和该时刻前7天对应时刻电价作为输入，该时刻电价作为输出。网络由200节点LSTM层和1层全连接层构成，采用ReLu激活函数和adam优化器，迭代100次。

采用8月1日—8月30日数据作为训练集，8月31日数据作为测试集，各方法预测结果对比如图3所示。可以看到由于日前价格较平稳的周期特性，M1预测曲线形状与真值较为相似，但存在凌晨至下午整体偏高、傍晚整体偏低的情况。由于训练数据量过少，基于数据驱动的M2—M4相较M1并未体现直观优势，M2、M4均未准确预测清晨至清晨的价格低谷，M3给出了过低的预测值(甚至低于最低限价，但本算例仅考虑模型输出值，不做二次处理)，M4仅在价格尖峰时段预测精度较高。

图3 日前价格点预测结果对比Fig.3 Comparison of point forecasting results of day-ahead price

3.2 传统评估指标结果分析

各传统评估指标对3.1节算例的预测误差指标如表1所示，各指标排序如图4所示。由表1可知，在最常用的3种指标中，MAE评估的最佳模型为M4，其指标值为26.38；MAPE和RMSE评估的最佳模型为M2，其指标值分别为17.53与32.87。从图4中可以看到，在5个指标中，有3个认为M2方法预测最小，但有2个认为M2排序第三；有2个认为M4方法预测误差最小，其余指标中M4排序第二或第三。

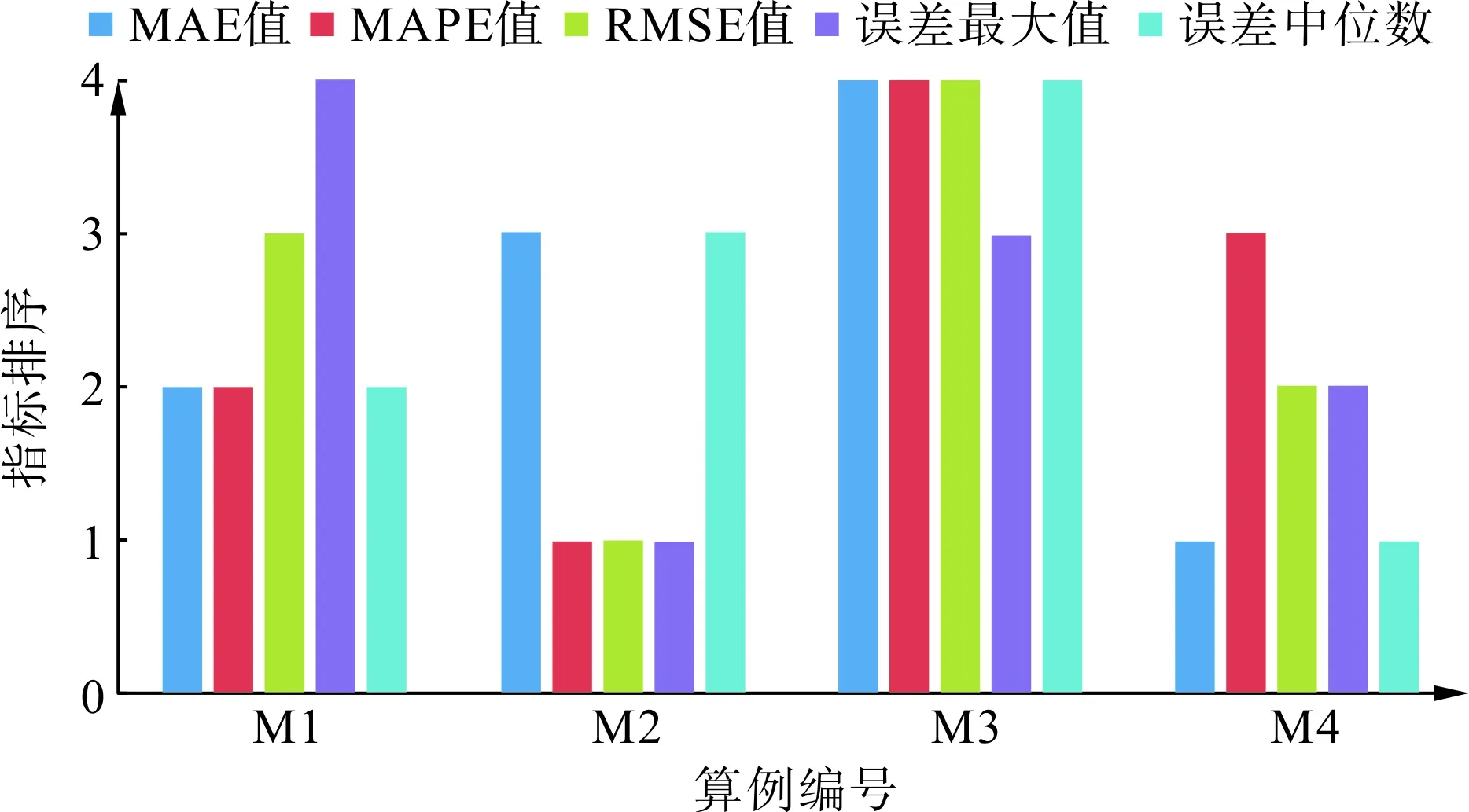
图4 传统误差评估指标排序Fig.4 Rank of traditional error indexes

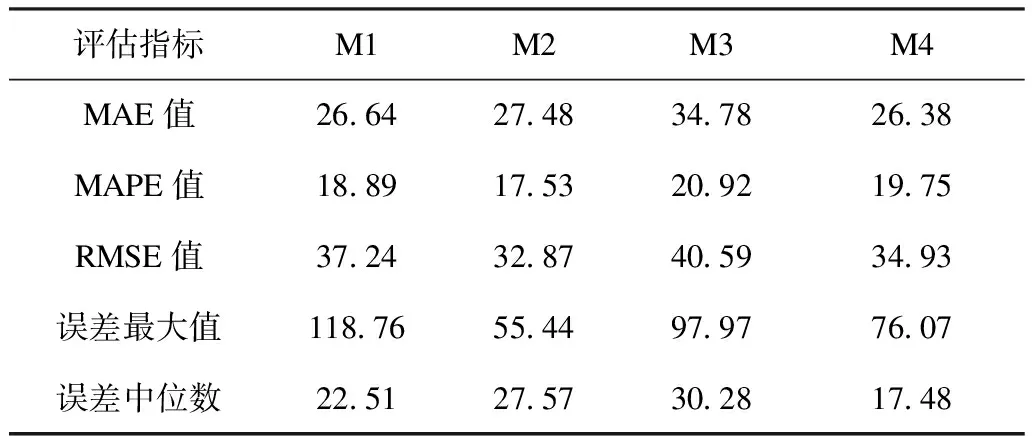
表1 传统误差评估指标结果Tab.1 Comparison of traditional error indexes

可以看到，采用传统指标分析预测误差，出现了各指标出现歧义，导致难以选取最佳预测模型的情况。若根据投票原则选取M2为最佳模型，会发现其在系统运营商、发电商使用场景中都产生了更大的风险偏差(见3.3节)，可见采用传统指标可能引发错误的模型选取结果。

3.3 风险评估指标结果分析

本节分别应对系统运营商、发电商、售电商的预测价格使用场景，计算各场景的风险评估指标。

1)场景1：系统运营商视角如式(7)—(9)所示，设置dt为预测日日前竞价空间；

2)场景2：发电商视角如式(10)所示，wgen,t取机组日前中标电量；

3)场景3：售电商视角如式(11)—(12)所示，不计实时电价预测误差。

4)场景1—2使用的竞价空间、合约分解系数如图5所示。

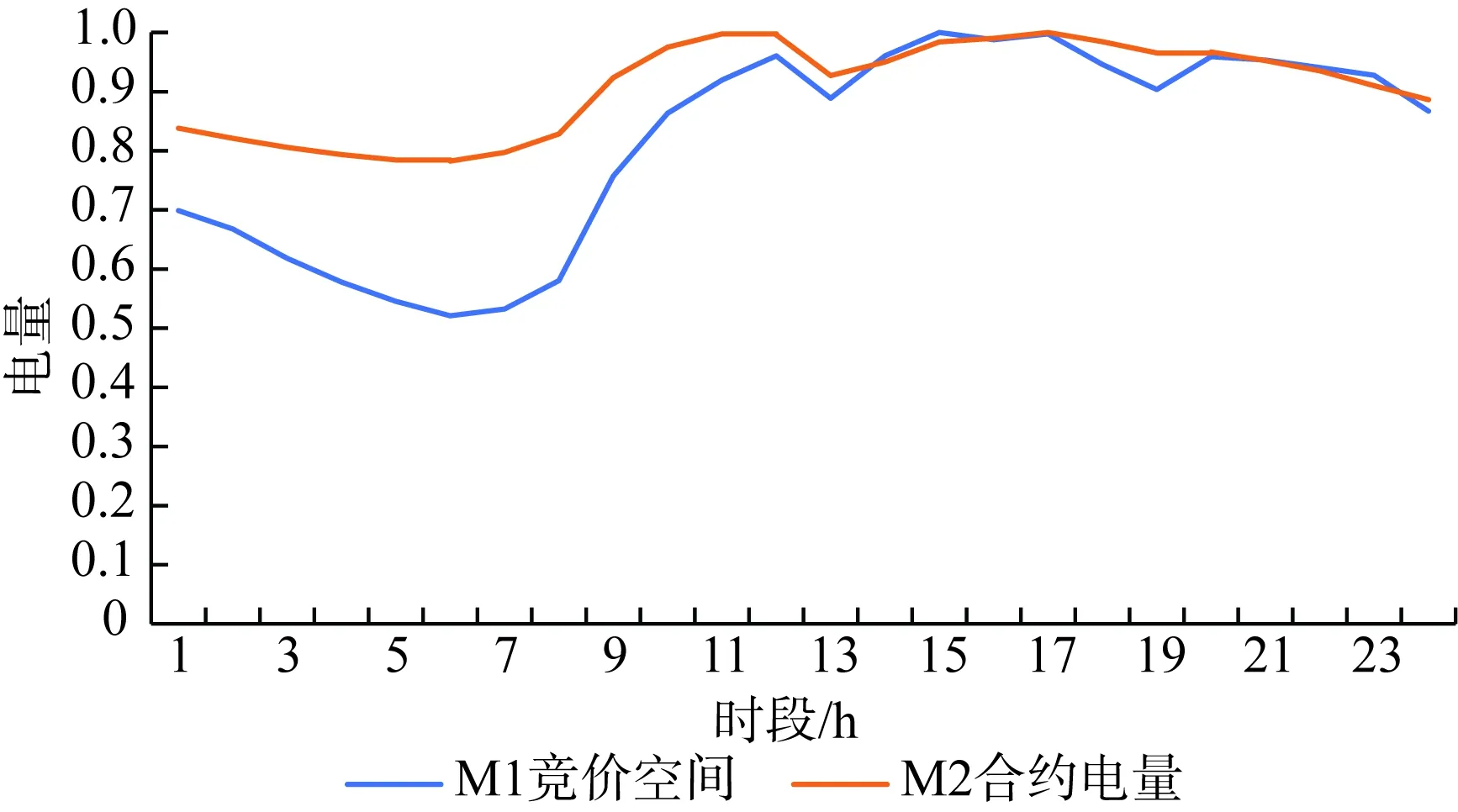
图5 M1—M2电量分解曲线(归一化后)Fig.5 Power decomposition curve of M1—M2(normalization)

各场景风险评估指标如表2所示，各指标排序如图6所示。可以发现根据使用场景的不同，风险评估指标给出了不同的模型推荐：场景1下系统运营商关注误差交易电量更大且对高误差给予更多惩罚，采用相似日法的M1预测模型各时段均存在一定误差，但由于相似日与预测日电价波动趋势相近，最大误差较小，基于此风险指标评价M1模型为最优模型；场景2下发电商关心日前价格预测误差对自身预期收益的影响，根据图5可知该发电商在9—14时段合约电量最高，该时段内的预测误差风险也最高，而M4模型在该时段内的预测误差较小，基于此风险指标判断M4模型对预期收益影响最小，为6.04万元，比排序第2的M1少400元，因此该场景下M4模型为最优模型；场景3下售电商考虑通过策略性报量盈利，此时M1方法虽然在传统指标下预测精度不佳，但其准确地反映了日前价格与实时价格的高低趋势，在该角度下优于其他3种预测模型。

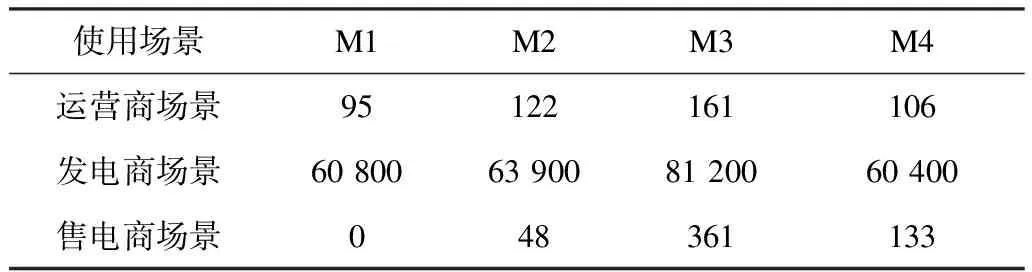
表2 风险评估指标结果Tab.2 Risk assessment indexes of different scenarios元

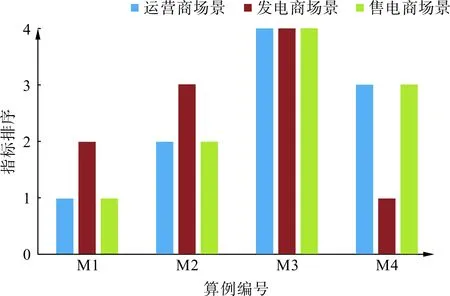
图6 风险评估指标排序Fig.6 Rank of risk assessment indexes

上述仿真表明，风险评估指标针对每一种场景具有唯一的判断结果，不会出现指标间存在歧义导致难以选取最优模型的情况。此外，风险评估指标能根据运营商及不同市场主体的决策特性及风险偏好，在各预测模型中选出最有利于其提升收益、降低风险的模型，该模型可能并不是传统指标认为的预测误差最小的模型。

3.4 工业用户实际决策分析

为进一步说明本文所提指标能帮助市场主体获取更高收益，本节考虑某工业用户使用预测电价进行用电计划安排，对比传统指标及风险评估指标选出最佳模型的收益情况。假设某自来水厂需要按照用水需求向城市供水，自来水厂拥有蓄水池，也可以使用电动水泵抽取地下水，其优化空间为在电价较低时使用水泵蓄水，电价较高时从蓄水池放水。自来水厂决策模型为制定使购电成本最少的水泵运行计划，同时满足用水需求和蓄水池水位约束，具体如式(18)所示。

(18)

式中：ui,t为水泵i在t时刻的开关状态，ui,t∈{0,1}；I为水泵数量；Pmax,i为水泵i最大运行功率；ht为蓄水池t时刻水位；Dw,t为t时刻用水需求；A为蓄水池表面积；Qmax,i为水泵i每小时抽水量；hini、hmin、hmax分别为初始水位、水位下限、水位上限。具体参数取值及水量需求数据取自文献[25]。该优化问题为MILP问题，本文使用Cplex求解。

分别使用8月31日日前电价真值及模型M1—M4预测值，求解自来水厂水泵运行计划，如附录图A2所示。将水泵运行计划带入日前电价真值得到使用不同预测模型的真实购电成本，如式(19)所示。

(19)

之后使用式(17)计算风险评估指标，设置权重为水泵运行功率。购电成本与风险指标值的数值如表3所示，不同预测模型的排序如图7所示。可以看到采用电价真值作为决策模型输入，理论购电成本是为2 775.15元，是所有算例中最低的，此时风险指标值为0，也是所有算例最低的。若采用预测电价替代真实电价作为决策模型参数，自来水厂制定的用电计划将偏离最优点，导致购电成本提高。在4种模型中，使用M1产生的购电成本最低，较理论成本偏高2.32%，风险评估指标也给出了同样的判断结果，若采用传统指标投票原则选出的误差最小模型M2，其购电成本将较理论成本高4.16%。从图7排序对比中可以看到，风险指标排序与实际购电成本排序完全相同，说明该风险评估指标能辅助用户选择更合适的电价预测模型。

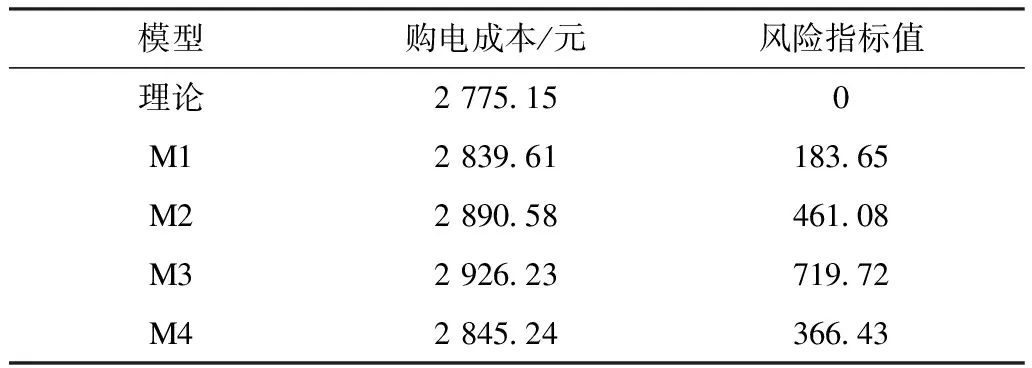
表3 各模型购电成本及风险指标Tab.3 Costs and risk assessment indexs of different models

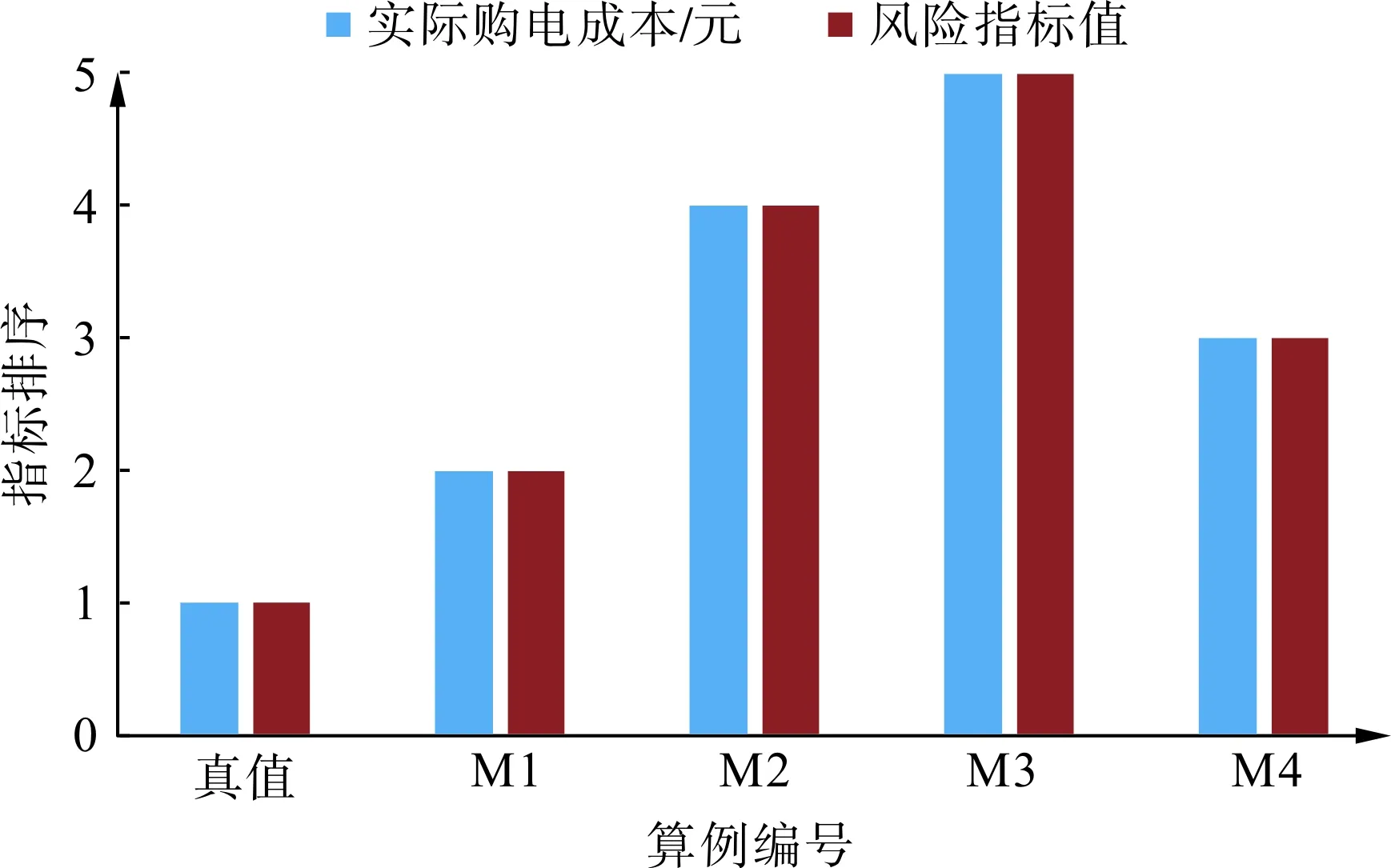
图7 购电成本风险评估指标排序Fig.7 Rank of assessment index and cost of electric power purchase

5 结论

在价格波动频繁、市场供需及参与者行为不确定性较高的现货市场中，准确的价格预测难度较大，不同预测模型由于数据或模型层面的局限性必然存在一定误差。传统预测模型误差评估指标可能出现多个指标排序结果不一致导致难以准确评价模型优劣，本文提出的风险评估指标可以根据预测主体的实际需求设置指标，具有反映主体误差风险成本、判断结果唯一等优点。在实际应用中，系统运营商可以将本文所提指标运用于事前风险评估体系中，通过选取更适合的价格预测模型降低由于预测不准导致的市场风险。除此之外，市场主体也可参考本文风险指标原则设计符合自身利益的评价指标，从而选取更适合的价格预测模型为参与市场博弈提供保障。算例结果表明工业用户使用本文所提方法后，购电成本下降1.76%～2.97%。