基于频差回归-差分观测共视授时模型的高精度同步时钟

雷金勇，白浩，黄秉开，袁智勇，潘姝慧，曾家琛，喻锟

(1. 南方电网科学研究院，广州510663；2. 广东电网有限责任公司惠州供电局，广东 惠州530600；3. 长沙理工大学电气与信息工程学院，长沙410114)

0 引言

随着北斗系统授时产品开始在全国范围内广泛应用，高精度授时日益广泛和普及。虽然目前卫星授时技术能够满足工作和生活中的大多数需求，但某些精细作业领域要求微秒级甚至是纳秒级的时间精度[1 - 2]，例如在电力系统故障测距中，建立行波传输到两端的时间差和故障点到两端的距离的关系，可实现对故障点精确定位[3 - 5]。但在采用双端行波定位原理进行故障测距时，行波在架空线的波速度接近光速，1 μs的时间测量误差就会导致300 m的测距误差[6]。时钟信号精度低和稳定性差的问题将导致这些技术难以在电力系统故障检测中得到广泛应用[7]，如何提高授时精度和稳定性受到了广泛的关注[8]。

近年来，通过卫星时钟和晶振时钟融合产生高精度时钟的技术得到了快速发展，文献[9 - 10]提出根据卫星时钟和晶振时钟授时特性互补的特点，校准GPS时钟信号的随机误差和修正晶振时钟信号的累积误差。文献[11]提出在基于晶振时钟和卫星时钟互补的授时模型上采用数字锁相原理改善对卫星信号的跟踪性能，实现高精度同步时钟的产生。文献[12]提出采用偏最小二乘回归的方法改善基于晶振时钟和卫星时钟互补授时的模型，提高同步时钟的精度；但目前的卫星和晶振融合产生高精度同步时钟的方法都未考虑直接修正卫星秒时钟随机漂移误差。文献[13]采用一种基于插值和卡尔曼滤波的方法预测卫星秒时钟随机漂移误差，但存在较大计算量的问题。对此本文提出了差分观测共视授时方法对卫星和晶振的融合时钟进行进一步修正。

差分观测共视授时是一种可以实现高精度时间频率传递的模型，其已作为各时间实验室的原子钟比对的主要方法。文献[14]详细介绍了GPS载波进行共视时间传递的方法。文献[15]提出了一种新型GPS共视时间传递系统设计方案，降低了共视接收机的成本。文献[16]分析了卫星秒时钟信号在空间传输中的误差对共视精度的影响；文献[17]针对GPS共视技术中的测量不确定度进行了分析和评定。文献[18]提出了一种新的基于共视原理的卫星授时新方法，并提出了虚拟共视基准站技术，减小了距离对共视技术的影响。文献[19]对超长基线的共视法授时进行了研究。文献[20]采用改进型卫星共视法，解决了传统卫星共视法存在间断，且不能灵活设置共视周期及实时输出比对结果的问题。对于高精度时间频率传递和区域内多个用户端时间同步的需要，差分观测共视授时提供了一种精确稳定的卫星秒时钟差分网授时模型，以保证用户与基准站的卫星秒时钟频率同步。

为提高电力系统授时的精度和稳定度，本文提出了一种基于频差-差分观测回归共视授时模型的高精度同步时钟生成方法。该方法通过采用差分观测共视授时模型建立卫星授时差分网减小用户卫星秒时钟信号在传输过程中随机漂移误差的影响，从而减小卫星秒时钟随机漂移误差，对卫星秒时钟进行修正。用修正后的卫星秒时钟信号作为参数提高晶振秒时钟与卫星秒时钟的频差回归模型的拟合精度，提高同步时钟的准确度与稳定性。

1 卫星秒时钟和晶振秒时钟的频差回归模型

1.1 卫星秒时钟模型

卫星授时中出现的各种误差可分为系统误差和随机误差[21 - 22]，其中系统误差可以通过建立误差模型或经验改正公式进行修正，而随机误差则服从正态分布，即：

ε～N(0,σ2)

(1)

式中：ε为卫星秒时钟随机误差；σ为标准差。

考查秒时间序列X=1, 2, 3, 4, …,x, …,n，则卫星输出的秒时钟序列可记为：

1-ε1, 2-ε2, 3-ε3, 4-ε4, …,x-εx, …,n-εn

卫星输出的第x个秒时钟y′x的通用公式如式(2)所示。

y′x=x-εx(x∈N)

(2)

则第x个卫星秒时钟时间误差为μ′(x)=εx。

1.2 晶振秒时钟模型

晶振秒时钟存在较大的累计误差，其频率稳定度在109Hz下产生的随机误差小于1 ns，所以可不考虑晶振秒时钟的随机误差[23]，设晶振秒时钟和国际标准时间进行时间同步的初始偏差和秒周期的初始偏差分别为a和R，每个秒时钟内的固定偏移误差为d；计第x个秒时钟与国际标准时间的偏差ΔTx为[24]：

ΔTx=R+dx

(3)

晶振输出的第x个秒时钟与国际标准时间的偏差μ″(x)为：

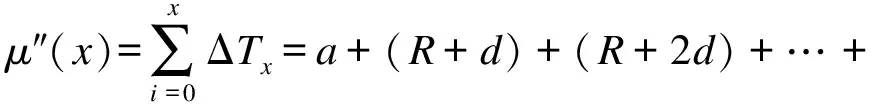
(4)

记b=R+d/2、c=d/2，则晶振秒时钟产生的时钟序列对应的国际标准时间可记为：1+a+b+c, 2+a+2b+22c, 3+a+3b+32c, …,x+a+bx+cx2, …,n+a+bn+cn2。

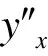
(5)

则第x个晶振秒时钟的时间误差μ″(x)为[11]：

μ″(x)=a+bx+cx2

(6)

可得晶振秒时钟与卫星秒时钟的偏差的频差回归模型yx为：

(7)

国际标准时间秒时钟Cu(t)、晶振秒时钟Ck(t)、卫星秒时钟Cb(t)的授时特性如图1所示。

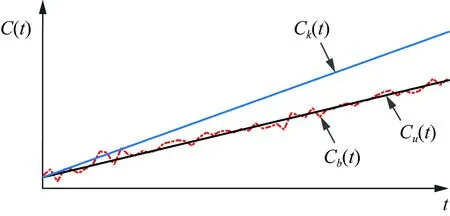
图1 秒时钟授时特性Fig.1 Characteristics of second clock timing

由图1可知晶振秒时钟存在一定的累积误差，卫星秒时钟存在围绕UTC秒时钟左右漂移误差。

1.3 频差回归模型

选择一组正交多项式，如式(8)所示。

(8)

(9)

则回归方程变为：

yx=b0φ0(x)+b1φ1(x)+b2φ2(x)+εx

(10)

系数b0、b1和b2的估计值分别为：

(11)

(12)

(13)

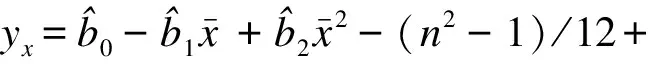
(14)

实时获取卫星时钟、晶振时钟的数据，对实时获取的数据使用频差回归模型进行实时估计，得到晶振秒时钟累积误差的估计值，并对频差回归模型进行更新。依据晶振秒时钟累积误差的估计值对晶振秒时钟进行补偿即可产生修正后的同步时钟。

2 差分观测共视授时模型

通过卫星秒时钟和晶振秒时钟互补特性建立误差回归模型获得同步时钟的方法可以弥补晶振秒时钟在长时间授时情况下的偏移误差[25]，但未对卫星时钟产生的随机漂移误差作预处理。本节通过建立差分观测共视授时模型实现对减小卫星时钟的随机漂移误差，以进一步提高频差回归方程的拟合精度。

2.1 单差分观测模型

差分观测共视授时即两用户站接收机同时观测同一卫星的秒时钟信号，其示意图如图2所示。

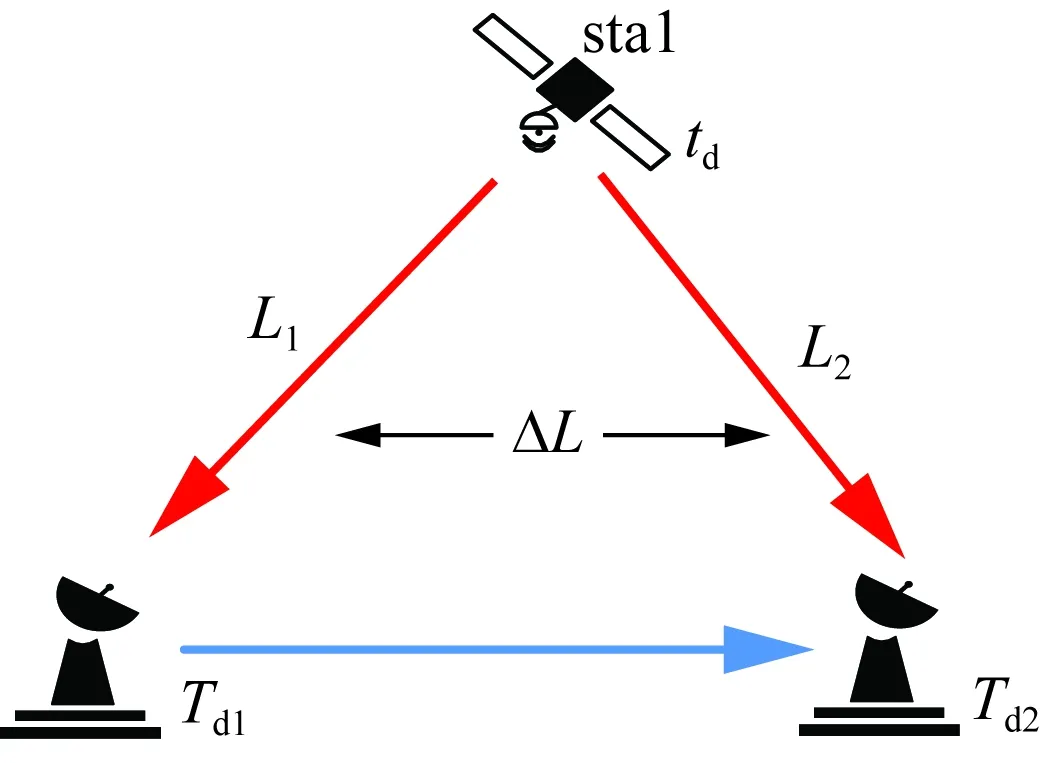
图2 差分观测共视授时示意图Fig.2 Diagram of differential observation common view timing

根据图2，对差分观测共视授时作进一步分析。对两用户站，每个用户站的观测量分别简写为L1和L2，每个用户站的接收机钟差分别为Td1和Td2。

观测方程相位的表达式如式(15)—(16)所示。

L1=ρ1+Ctd-CTd1+TTrop-TIon+ξ1

(15)

L2=ρ2+Ctd-CΔTd2+TTrop-TIon+ξ2

(16)

式中：L为用户的接收机对卫星的已知相位观测值，由用户和卫星所在历时时刻的坐标获得；ρ为卫星至接收机的伪距，由用户终端测得；td为卫星钟差；Td为接收机钟差；TTrop和TIon分别为对流层延迟和电离层延迟；ξ为观测值其他噪音；C为真空中的光速；下标数字1或2表示用户标号。

当两测站间距很短时(小于100 km)，可认为卫星秒时钟信号至两个测站所经过的大气条件相同，即对流层延迟和电离层延迟相同，组成站间求差即可消除TTrop和TIon误差。

对两用户站的观测量做差得到差分观测量ΔL：

ΔL=Δρ-CΔTd+Δξ′

(17)

2.2 卫星秒时钟差分网

根据差分观测模型设立一个基准用户，使这个基准用户成为所有用户接收机用于测定相对时钟偏差的公共端。

当两测站所用接收机性能相近时，可忽略Δξ′， 通过已知的两测站坐标，计算得到两站用户的相对接收机钟差模型ΔTd为：

(18)

如图3所示，以所有用户所在的地理位置为选取范围，选取范围内在地理位置上最靠近中心的用户作为基准用户，以基准用户站接收机本地时间作为基准时间。用户站可采用Internet网络、GPRS、通信卫星等通信链路实时将用户接收机获得的伪距、相位观测值数据发送至基准站后台，后台接收数据后按差分观测共视授时模型处理得到每个用户站在基准时间下的接收机钟差模型，并通过通信链路将接收机钟差模型向覆盖区的用户站广播，用户站观测同一卫星获得该卫星系统时间，对该时间根据接收机钟差模型进行补偿，完成用户站的授时。

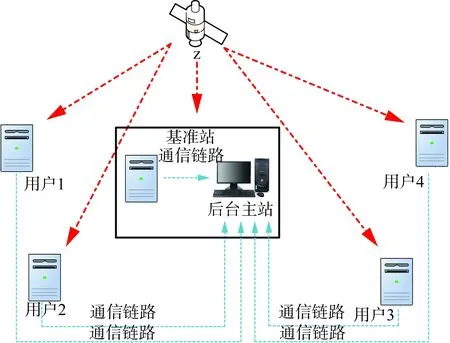
图3 星形卫星授时差分网Fig.3 Time difference network for star satellite

以接收机钟差为接收机本地时间与基准时间的时间之差，则有：

ΔTp=0，ΔTdpp1=ΔTp-ΔTp1=-ΔTp1

(19)

式中：ΔTp、 ΔTp1分别为基准用户接收机钟差和用户接收机钟差；ΔTdpp1为基准用户与用户相对接收机钟差。

计算得到用户接收机钟差ΔTp，对用户端接收机钟差进行在线修正，从而减小卫星秒时钟随机漂移误差e。当多个用户与基准站用同一卫星进行授时时，可形成局部的卫星授时网络。在采用差分观测共视授时模型后，被消去的误差如：电离层、对流层延时(2 ns)、接收机钟差误差和卫星钟差(8 ns)[1]，卫星秒时钟随机误差的标准差至少可减少10 ns。

2.3 同步时钟精度分析

对于卫星秒时钟，其方差σ2=D(ε)=E(ε2)是ε的二阶原点距，按距估计法有：

(20)

晶振误差估计值μ″(x)， 服从正态分布。

(21)

根据一元二次回归分析的性质得的回归方程方差D(y)为：

(22)

在正交一元二次多项式中，有：

(23)

把式(23)代入式(22)得：

(24)

把式(8)代入式(24)得：

(25)

当x=n时有最大值Dmax(y)为：

(26)

设P为频差回归方程的最大方差与卫星秒时钟误差方差的比值Dmax(y)/σ2， 可反映修正后的同步时钟所含误差大小，P与修正后同步时钟秒时钟样本数n的关系如表1所示。

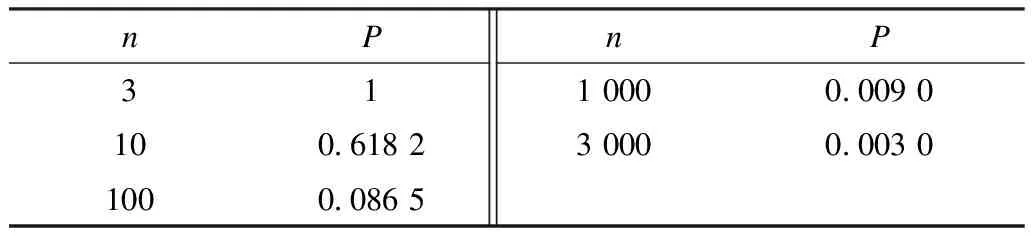
表1 P与修正后同步时钟样本数n的关系Tab.1 Relationship between P and sample number n of modified synchronous clock

由表1可知：修正后同步时钟样本数n越大，P越小，即修正后的时钟偏差越小。当n>3时，Dmax(y)<σ2=D(ε)， 修正后的同步时钟误差小于卫星秒时钟直接授时误差。当n>100时，式(26)可近似化简为：

(27)

综上所述，若选取连续1 000个同步时钟秒时钟样本，选取标准差为50 ns的卫星接收机进行频差回归方程的最大方差的计算，由(27)式可得：

(28)

表示在经过1 000次的频差回归模型修正后的误差至少有0.682 8的概率要小于4.743 4 ns。要远小于未经修正的接收机标准差50 ns。随着同步时钟秒时间的样本数越多，频差回归模型迭代次数越多，修正后的同步时钟时钟最大方差会越小。

由式(20)—(25)可知，D(y)与e成正相关，e减小使得晶振秒时钟与卫星秒时钟的频差回归模型方差D(y)减小。采用差分观测共视模型使得方差减小不仅可以降低同步时钟最大误差值，提高同步时钟的精确度，而且能减小整个授时过程中同步时钟的平均误差，增强同步时钟的稳定性。

3 仿真验证

为验证基于频差-差分观测回归共视模型可以产生更高精确度和稳定性的同步时钟，本文在MATLAB仿真软件上进行了一系列仿真实验。卫星时钟的随机漂移误差以s=50 ns的高斯噪声进行模拟；晶振时钟的晶振频率设为200 MHz，频率精度为10-9s，频率稳定度为10-11/s，晶振温度稳定为50 ℃。

依据正交多项式分析步骤对同步时钟误差进行实时计算和更新，获得修正后的同步时钟误差曲线如图4—5所示。

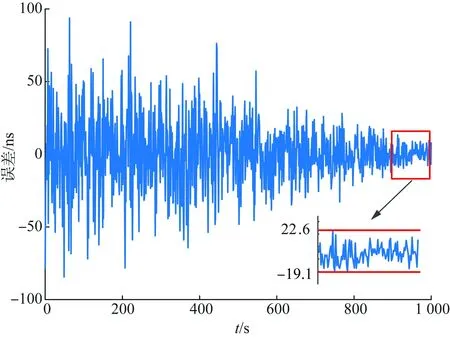
图4 基于频差回归修正的误差Fig.4 Error correction based on frequency difference regression

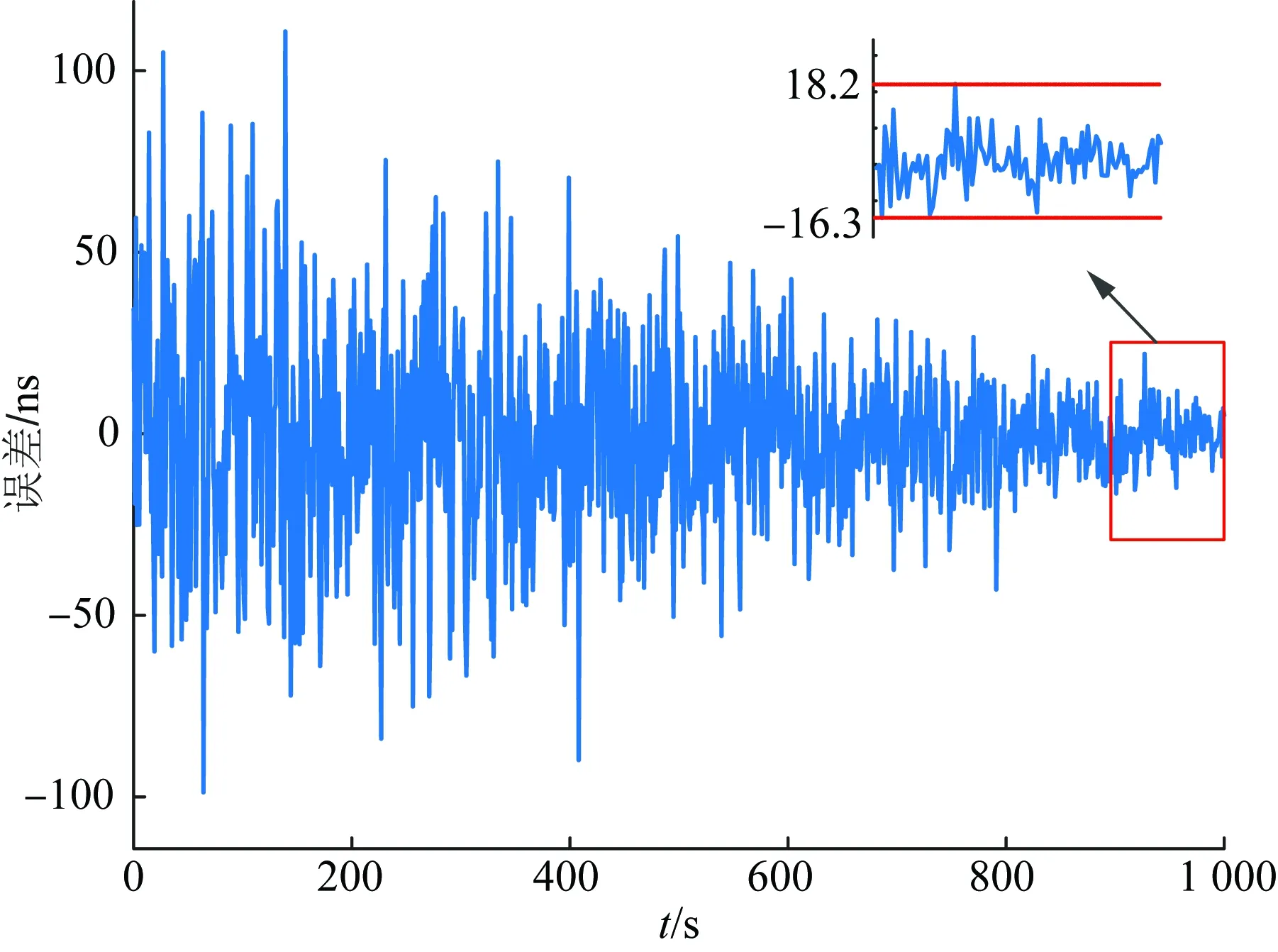
图5 基于频差回归-差分观测共视授时修正的误差Fig.5 Error correction of common-view timing based on frequency difference regression-difference observation

修正后的同步时钟误差仍然符合随机漂移误差特性，但随着同步时钟样本数越大，修正后的同步时钟误差变得越小，说明了该模型在长时间的运行下能得到更精确的同步时钟。

3.1 卫星授时失效时的同步时钟

卫星授时失效后，对用户站的授时改为晶振单独授时，通过卫星授时失效前的n次秒时钟样本数据取平均值，作为晶振秒时钟的补偿值，卫星秒时钟失效后的误差曲线如图6所示。

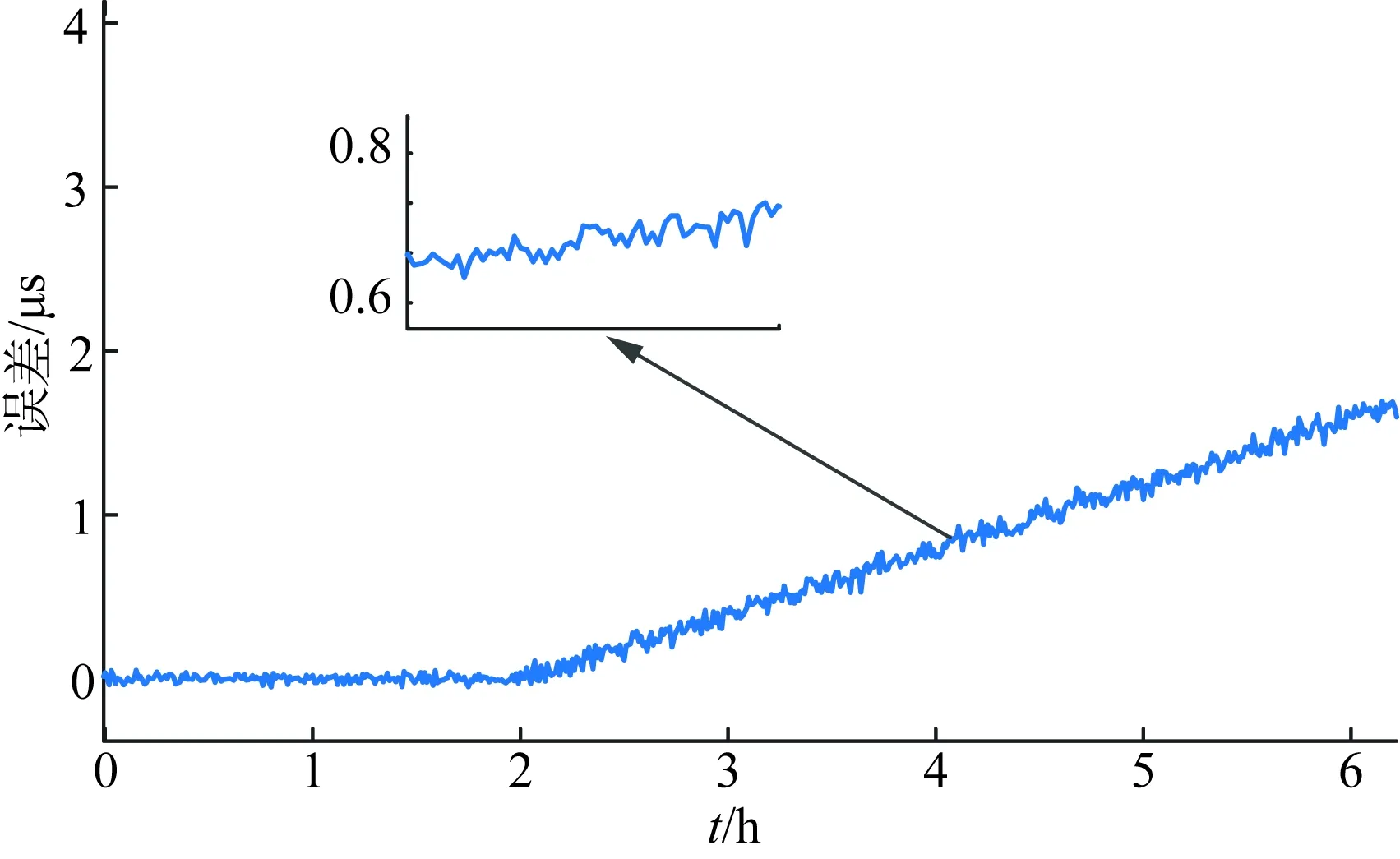
图6 卫星秒时钟失效后的误差Fig.6 Errors after satellite clock failure

图6中局部放大区域对应于卫星秒时钟失效后2 h的误差曲线。可以看出当卫星秒时钟在第2 h失效后，虽不再能很好地消除同步时钟的累积误差，但在失效后的第2 h其误差仍小于0.8 μs，要优于智能变电站授时标准1 μs/h的要求。

3.2 同步时钟误差对比分析

差分观测共视模型直接减少卫星秒时钟的随机漂移误差，将本文提出的基于频差回归-差分观测共视授时方法与现有的同步时钟技术中采用最小二乘法进行对比，截取稳定后一定时间窗内的误差曲线如图7所示，其中m1为卫星直接授时的误差曲线，m2为采用频差回归模型授时的误差曲线，m3为在频差回归模型基础上采用差分观测共视授时模型进行修正后的授时误差曲线。

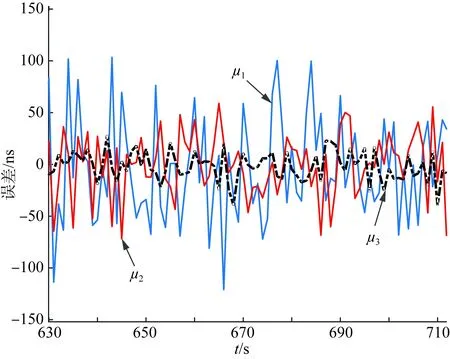
图7 时钟误差对比Fig.7 Clock error comparison

由图7可以看出，卫星直接授时的误差达到100 ns以上的次数明显较多，采用频差回归模型秒时钟授时误差可达50 ns以上，而采用频差回归-差分观测回归模型进行修正后，授时误差基本稳定在50 ns以内。

该时间窗内各授时模型的最大误差和平均误差的统计如表2所示。

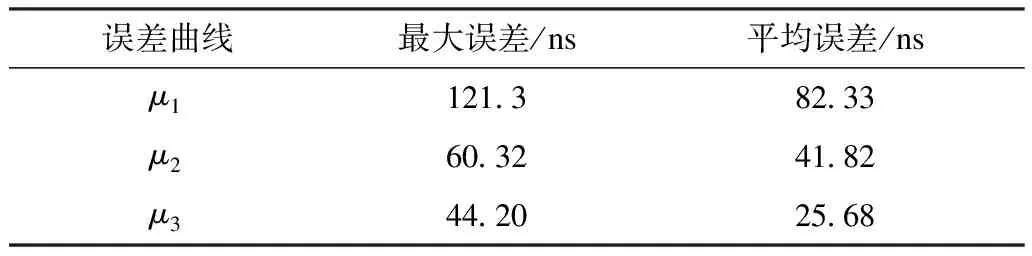
表2 最大误差与平均误差统计表Tab.2 Statistical table of maximum error and average error

由表2可知采用频差-差分观测回归共视模型后最大误差由121.3 ns减小到了42.4 ns，同步时钟的精确度明显提高；且平均误差由82.33 ns减小到了25.68 ns，具有更好的稳定性。

由仿真结果可知，与晶振秒时钟和卫星秒时钟相比，采用频差-差分观测回归共视授时模型减小了同步时钟的随机误差和累积误差，有效提高了同步时钟的精确度和稳定性。

4 结论

利用卫星秒时钟与晶振秒时钟授时特性互补的特点，结合差分观测共视授时原理，提出了基于频差-差分观测回归共视授时模型的高精度同步时钟的方法，该方法采用差分观测共视授时模型减小卫星秒时钟信号在传输过程中产生的随机漂移误差的影响，对卫星秒时钟进行修正，用修正后的卫星秒时钟信号作为参数提高晶振秒时钟与卫星秒时钟频差回归模型的拟合精度，提高同步时钟的精确度。在测区范围适中，用户站几何距离合适的情况下，能有效提高卫星授时差分网内的授时精度，有望广泛应用于故障行波定位等对时间同步性能要求高的电力系统控制保护领域。