考虑集中荷载影响的超高压孤立档相间间隔棒长度计算方法

方萌，文中，姜岚，孟遂民，符文熹，魏炘，王海涛

(1. 三峡大学电气与新能源学院，湖北 宜昌443002；2 湖北能源集团鄂州发电有限公司，湖北 鄂州436000；3. 湖北省输电线路工程技术研究中心(三峡大学)，湖北 宜昌443002； 4. 四川大学水利水电学院，成都610065；5. 国网四川省电力公司天府新区供电公司，成都610065)

0 引言

导线舞动是造成线路跳闸、断线、倒塔等事故的一个重要原因[1 - 6]。为了减少舞动对输电线路的影响，电网采取了一系列防舞措施，其中相间间隔棒便是一种使用比较广泛的防舞装置[7]。相间间隔棒由复合绝缘子和两端金具组成，将各导线机械地连接起来，使各导线的运动相互制约，以达到抑制舞动的目的[8 - 9]，因其具有良好的防舞效果而被广泛使用[10 - 11]。在传统的相间间隔棒长度计算方法中，未考虑集中荷载的影响，往往导致设计长度偏长，在工程中不得不通过大尺寸的调节板来弥补计算误差。与此同时使用调节板也带来了很多问题，如因长度过长，超出了调节板可调范围，导致无法安装；超出了分裂导线的分裂间距，看起来不美观，并由此会产生电晕损耗、可听噪声，增加有功损耗；导致相间间隔棒和导线连接处产生集中应力，容易磨损导线，长期以来会发生断股断线等电力事故，威胁电网的安全运行。

在工程设计中，一般假定线间距不变，根据塔头尺寸直接使用勾股定理来计算相间间隔棒长度，计算方法比较简单。国内外在相间间隔棒长度计算方面的理论研究较少，研究工作集中在导线弧垂计算方面。文献[11]通过理论计算和实测值验证了相间间隔棒自重对导线弧垂的影响。文献[12 - 13]通过理论分析和工程算例得出较长、较重的耐张绝缘子串对导线弧垂的影响不容忽视。文献[14]通过理论分析和工程实例验证了耐张串使用简支梁法和悬链线法对弧垂的影响较小。文献[15 - 17]通过理论分析和工程算例给出了孤立档和大档距导线弧垂的计算方法。文献[18 - 20]通过工程算例验证了可使用数值仿真方法计算导线弧垂。上述方法可对集中荷载的超高压孤立档弧垂进行计算，但并未与相间间隔棒长度计算联系。目前行业内仍然采用传统的勾股定理计算相间间隔棒长度。该方法可以快速地算出长度值，但在超高压输电线路中，导线耐张串和相间间隔棒质量较大，严重影响导线弧垂，不考虑相间间隔棒等集中荷载的影响，会产生许多问题。

本文通过考虑多种集中荷载对弧垂的影响，提出了一种新的相间间隔棒长度计算方法，可为孤立档相间间隔棒长度计算的研究和工程设计提供参考。该方法可较精确地计算相间间隔棒长度，可解决以往计算长度偏长的问题，减少输电线路的电晕损耗、可听噪声，提高输送效率，减少导线断股断线风险，对消除输电线路的安全隐患和提高输电线路的经济性具有重要的意义。

1 计算方法

1.1 集中荷载下孤立档架空线弧垂

架空导线除了有耐张串和相间间隔棒等集中荷载，还有均布荷载。采用相当简支梁法[1]，多集中荷载孤立档架空线弧垂公式可表示为架空线几何参数及荷载参数的函数，即：

1)当λ0≤x≤a1时，有

(1)

2)当ai-1≤x≤ai时，有

(2)

3)当an≤x≤l-λ0时，有

(3)

式中：fx为架空导线x处的弧垂；l为档距，x为距离左悬挂点的距离；n为集中荷载的数量；γ为导线的比载；γJ1、γJ2分别为左侧和右侧耐张绝缘子串比载；λ0为耐张串水平投影长度；β为高差角；τj为集中荷载单位截面重力；ai、aj为集中荷载距悬挂点A的水平距离；bj为集中荷载距悬挂点B的水平距离；σ0为架空线水平应力。

1.2 孤立档架空线状态方程式

架空线的弧垂是其比载、应力的函数。当气象条件发生变化时，架空线的长度会发生改变，该变化主要由温度变化产生的热胀冷缩量和弹性伸长量产生的弹性伸长组成。根据原始线长相等，经过力学分析和简化归并[1]可得孤立档导线状态方程式。

(4)

过牵引状态下的状态方程式[21 - 22]为：

(5)

式中：σ01、σ02分别为已知状态和待求状态下架空线的水平应力；t1、t2分别为已知状态和待求状态下的气温；K1、K2分别为已知状态和待求状态下的线长系数；l1为架空线所占档距；E为架空线的弹性系数；α为架空线的线性膨胀系数；ΔL为挂线时绝缘子串过拉长度。

经过力学分析和化简归并[1]可得竣工情况下两侧绝缘子串相同，有n个集中荷载的线长系数为：

(6)

式中：GJ为耐张绝缘子串荷载；τi为集中荷载单位截面重力；bi为集中荷载距悬挂点B的水平距离；A为架空线截面积；W1为架空线单位截面荷载，W1=γl1/cosβ；γβ为架空线的水平投影比载，γβ=γ/cosβ。

1.3 相间间隔棒长度计算

以500 kV常规型同塔双回输电线路上-中相为例进行计算。根据施工安装流程，相间间隔棒安装过程为先固定上端，再固定下端，因此在计算导线弧垂时，相间间隔棒的集中荷载由上端导线承担。

计算相间间隔棒长度的传统方法为直接根据塔头尺寸算得上-中相挂点的垂直距离和水平距离，再使用勾股定理计算直角三角形斜边，斜边即相间间隔棒长度。该方法未考虑集中荷载对弧垂的影响，不计算弧垂，计算得出的长度在整档内均一致，塔头尺寸相差较大和耐张塔转角较大时，分情况计算。本文先考虑耐张串和相间间隔棒自重等集中荷载对上相导线弧垂的影响，再分别计算安装点处上相和中相导线弧垂，最后根据塔头尺寸计算相间间隔棒长度。本文方法得出的长度随安装点不同而不同，塔头尺寸不同和耐张塔有转角度数时，分情况计算。

在不同温度下，导线弧垂会发生变化，相间间隔棒受力也不同，但在架空线运行过程中，年均温工况在各个工况中占比最大，因此按照年均温工况设计相间间隔棒长度比较合理。本文均在年均温工况下计算相间间隔棒长度，其他工况亦可根据状态方程式求出。

在实际工程中，往往两侧耐张塔塔头尺寸不一样，且有转角度数，下面将分不同情况进行讨论。假设某孤立档三相导线为垂直排列，耐张塔中相横担最长，上相和下相横担一样长，如图1所示。A、C点分别为上相和中相导线上任意一点，距离左悬挂点的水平距离为x， 上相导线弧垂为f1， 中相导线弧垂为f2， 左侧与右侧耐张塔上相与中相垂直距离分别为lv1、lv2， 水平距离分别为lh1、lh2， 相间间隔棒安装点垂直距离为lv， 水平距离为lh。 因此只要计算出lv和lh， 便可计算出相间间隔棒长度，长度即直角三角形斜边。

(7)

1.3.1 塔头尺寸相同情况下的计算

当塔头尺寸相同时，有lv1=lv2，lh=lh1=lh2， 如图1所示。

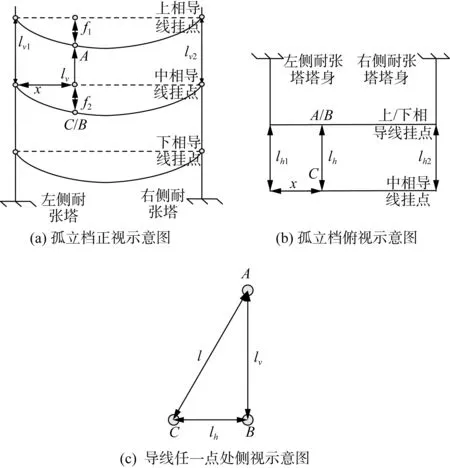
图1 塔头尺寸相同时孤立档示意图Fig.1 Schematic diagram of isolated gear with identical tower head sizes

此时安装点上-中相的垂直投影长度为挂点的垂直距离减去上相弧垂再加中相弧垂，即：

lv=lv1-f1+f2

(8)

水平投影长度为挂点间的水平距离lh， 相间间隔棒长度为直角三角形的斜边，即：

(9)

1.3.2 塔头尺寸不同情况下的计算

当塔头尺寸不同时，水平和垂直距离计算不同，如图2所示。

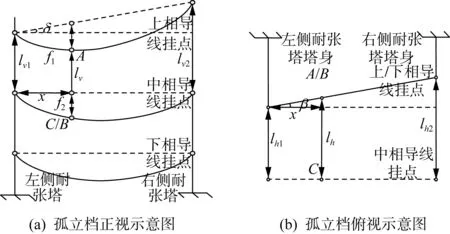
图2 塔头尺寸不同时孤立档示意图Fig.2 Schematic diagram of isolated gear with different tower head sizes

此时安装点水平距离为：

lh=lh1+xtanβ

(10)

式中β为左右侧耐张塔上相导线挂点与水平方向的夹角。

垂直距离为：

lv=lv1+xtanδ-f1+f2

(11)

式中δ为左右侧耐张塔上相导线挂点与水平方向的夹角。

1.3.3 耐张塔有转角情况下的计算

当耐张塔有转角度数时，因500 kV铁塔横担较长，两挂点的水平距离会受转角度数的影响，因此挂点间水平距离计算不同，如图3所示。

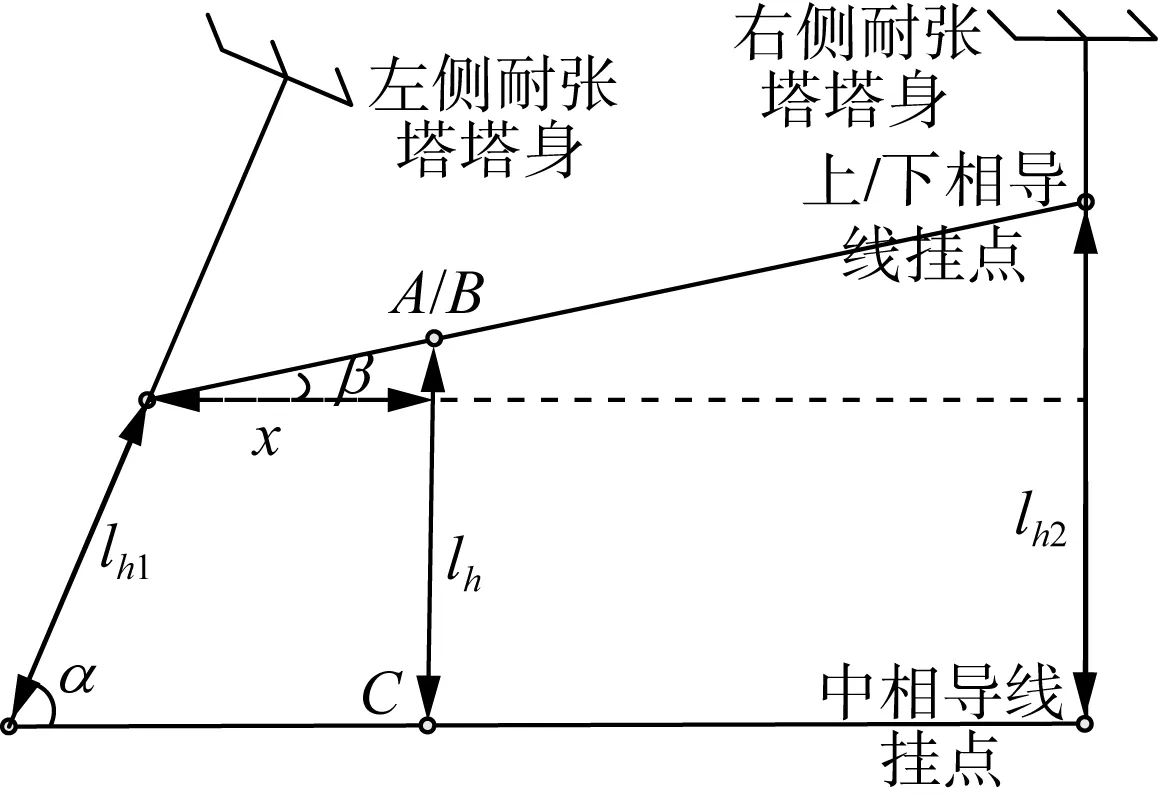
图3 孤立档俯视示意图Fig.3 Top view of isolated gears

此时安装点水平距离为：

lh=lh1sinα+xtanβ

(12)

式中：β为左右侧耐张塔上相导线挂点与水平方向的夹角；α为左右侧耐张塔中相导线挂点与左侧耐张塔之间的夹角。

其他情况均是以上3种情况的组合。如几何计算较复杂，可使用AutoCAD等绘图软件先根据塔头尺寸按比例画出安装点的三视图，再量出lh、lv即可。本文方法计算流程如图4所示。

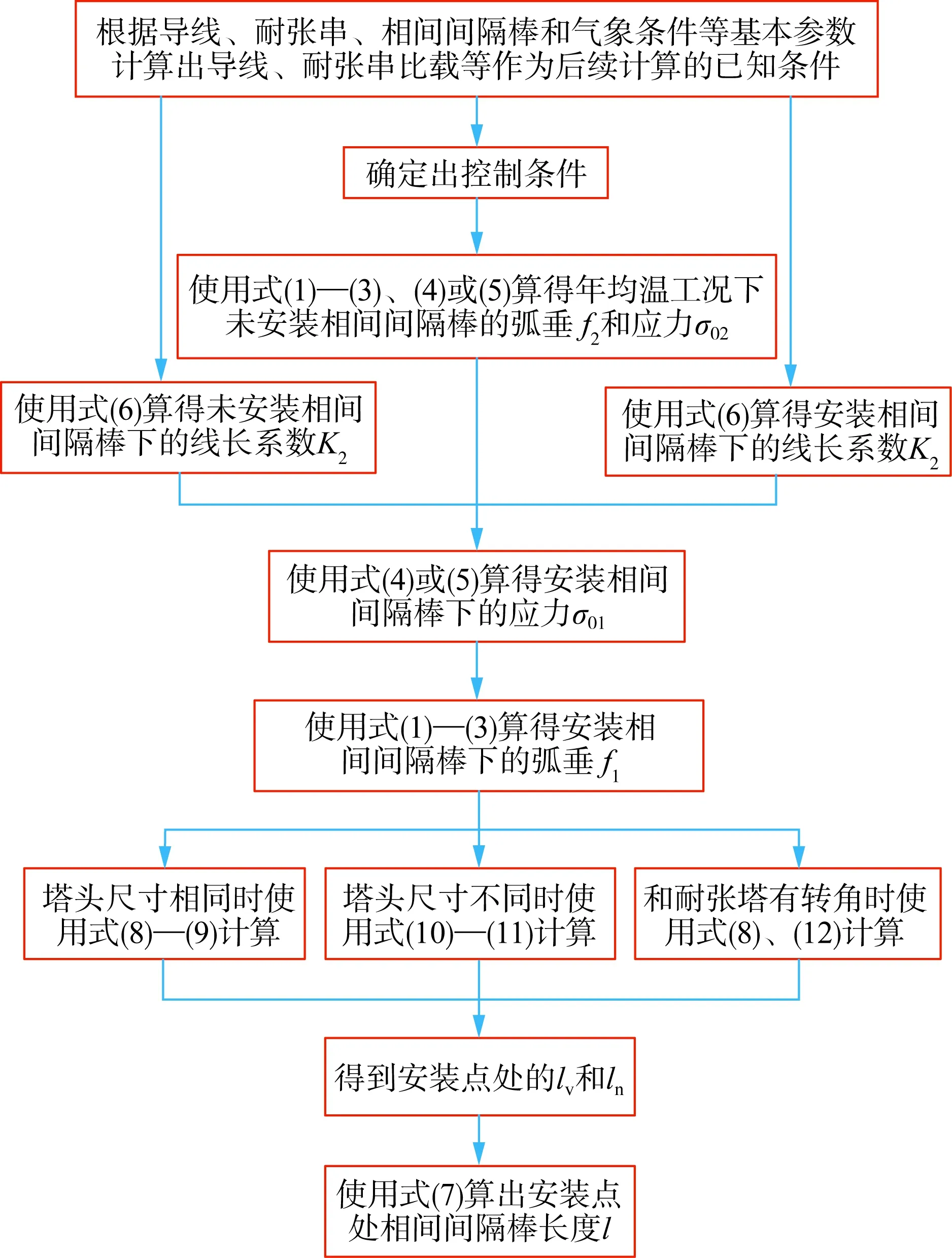
图4 本文方法计算流程Fig.4 Calculation process of the method in this paper

2 工程算例

2.1 计算参数的选择

为了验证本文计算方法与传统计算方法的差异，取湖北某条已投运的500 kV同塔双回输电线路中的一回设计参数为工程算例。导线采用4×LGJ-500/45型钢芯铝绞线，耐张绝缘子串长7.96 m，无冰串重1 014.8 kg，如表1所示。气象条件为湖北典型气象(基本风速27 m/s、覆冰10 mm)，如表2所示。左侧耐张塔为51SDJ151-24型，右侧为51SDJ151-30型，具体尺寸如表3所示；假定高差为0 m，耐张塔转角度数为0 °，档距范围为50～1 000 m，相间间隔棒重量为100 kg。

500 kV同塔双回输电线路相间间隔棒布置方法[23]如表4所示。由表4可知，随着档距变化，相间间隔棒的数量和安装位置均会发生变化，本次工程算例充分考虑了相间间隔棒的质量、数量和安装位置。

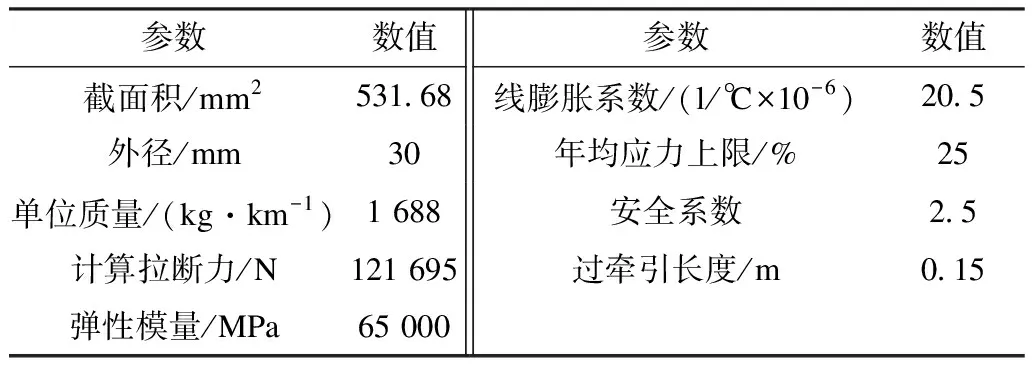
表1 输电线路LGJ-500/45型导线参数[23]Tab.1 parameters of the transmission wire LGJ-500/45

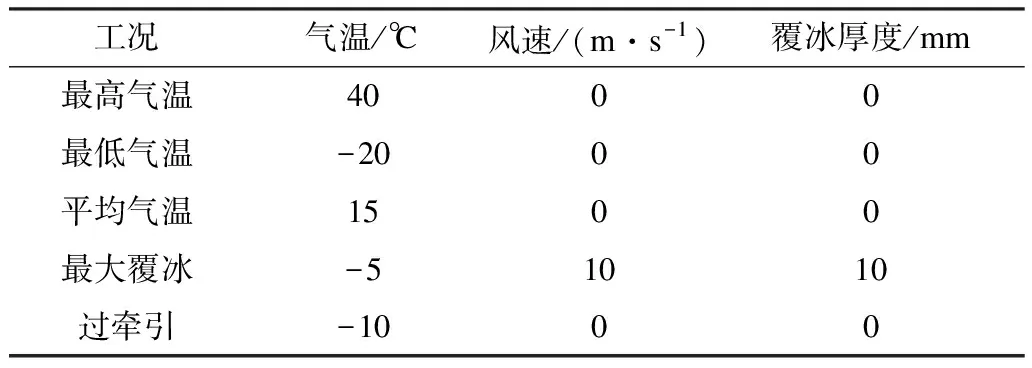
表2 气象条件表[24]Tab.2 Table of meteorological conditions

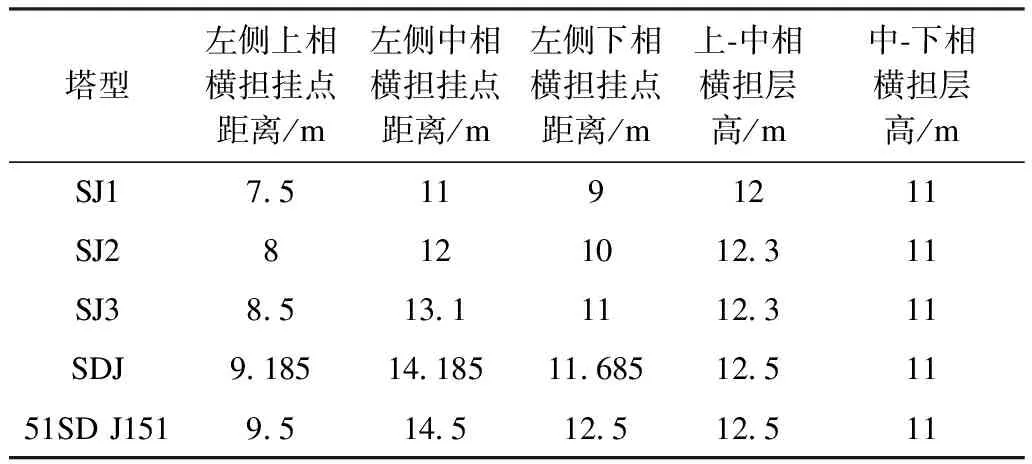
表3 塔头尺寸表Tab.3 Tower head size table

表4 500 kV同塔双回输电线路相间间隔棒布置方法[23]Tab.4 Arrangement method of interphase spacers for 500 kV double circuit transmission lines on the same tower

2.2 计算结果及分析

按照表4的布置方法，本文从左悬挂点开始分别命名为1、2、3、4号相间间隔棒，以上-中相安装相间间隔棒为例，分别列出档距从50～1 000 m情况下，本文方法和传统方法计算得到的数据图如图5—7所示。由弧垂的对称性可知，对称位置处导线弧垂与相间间隔棒计算长度一致，因此可省略对称位置的数据图。

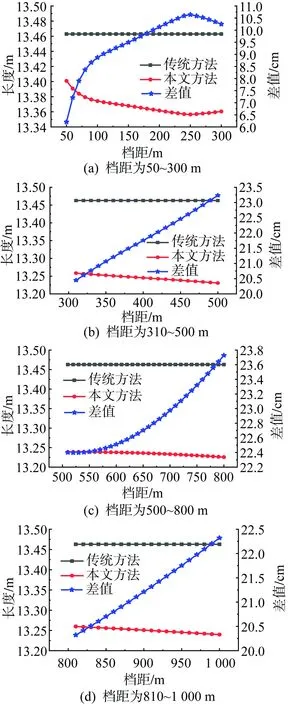
图5 1号相间间隔棒长度对比图Fig.5 Comparison chart of the length of No. 1 interphase spacer

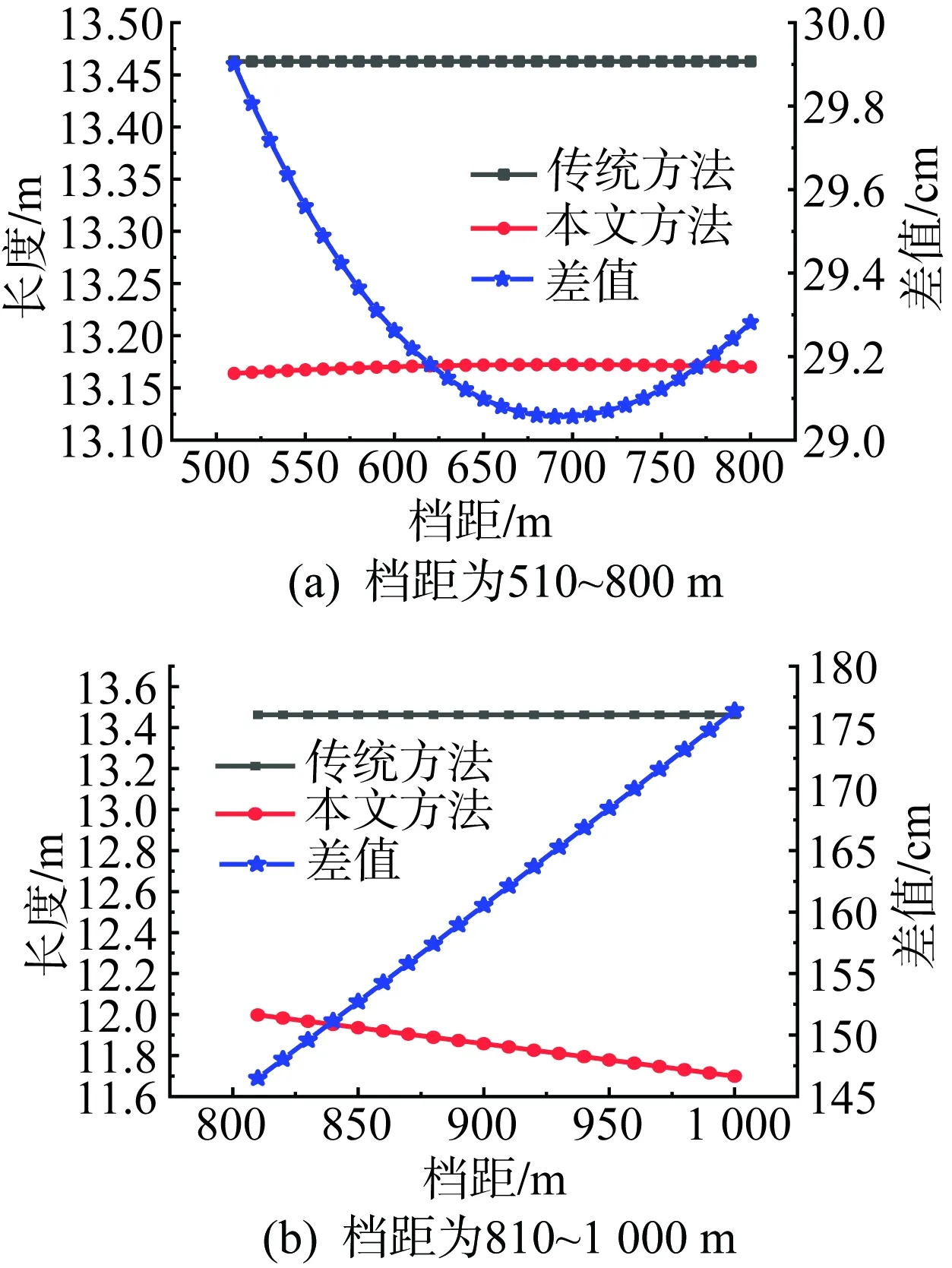
图6 2号相间间隔棒长度对比图Fig.6 Comparison chart of the length of No. 2 interphase spacers

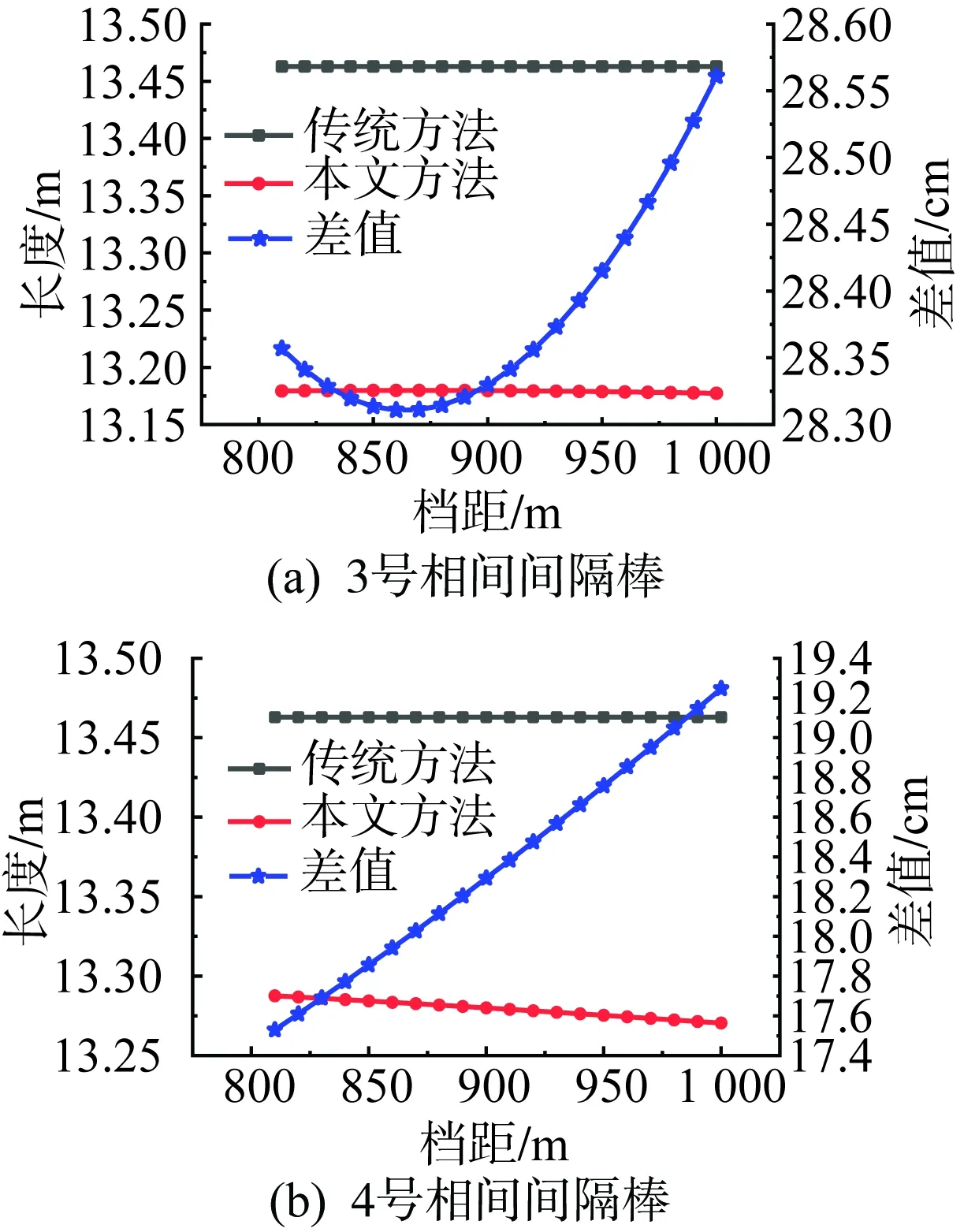
图7 档距810～1 000 m时3、4号相间间隔棒长度对比图Fig.7 Comparison chart of the length of No. 3、4 interphase spacers when the gear span is 810～1 000 m

可以得出，传统方法计算得到的相间间隔棒长度与档距无关，均偏长，为13.463 m，这也与湖北目前投运线路的相间间隔棒情况吻合。在同一档距范围内，档距中央以外，本文方法计算得到的相间间隔棒长度随着档距的增大呈现递减趋势，两者的差值呈递增趋势。在档距中央处，本文方法得到的相间间隔棒长度随着档距的变化不明显，两者的差值呈现先减后增的趋势。除了档距在810～1 000 m情况2号相间间隔棒以外，其他差值均小于30 cm；档距在810～1 000 m时2号相间间隔棒长度差值在146.5～176.3 cm，差值百分数在12.21%～15.08%。而在工程实际当中，孤立档档距在800 m以上且安装相间间隔棒的情况较少，因此这种情况较少遇见，比较隐蔽，不容易被发现。这种情况是由档距大、相间间隔棒安装数量较多，1、2号相间间隔棒安装间距较3、4号近，1、2、3、4号相间间隔棒安装位置不对称、不均匀，整体偏向档距中央左侧导致。

3 实测验证

3.1 实测概况

为了验证本文方法的正确性，对湖北境内2条500 kV线路进行了现场实测。首先用无人机找到合适的孤立档[25 - 26]，再对导线弧垂进行测量。本次导线弧垂测量采用中海达TS5 PRO GPS和中纬ZT10R PRO免棱镜全站仪。测量方法[27 - 28]为：首先用GPS-RTK流动站在每档线路的两边线50 m处布设控制点，然后用GPS-RTK流动站分别采取两侧塔位中心桩的坐标，再在控制点上架设免棱镜全站仪测量相间间隔棒安装点处上相和中相导线弧垂，最后将测得的数据相减即为相间间隔棒长度。为准确记录线路的弧垂情况，在相间间隔棒安装处实测了4个点，然后取其平均值。测量时气温为35 ℃、无风。

本次实测的2条500 kV线路导线型号均为LGJ-500/45，具体参数如表1所示。其中一条线路耐张串长7.91 m，无冰串重1 140.8 kg；另一条线路耐张串长6.91 m，无冰串重769.5 kg。其他计算参数如表3、表5所示，其中右侧耐张塔高时高差为正值。

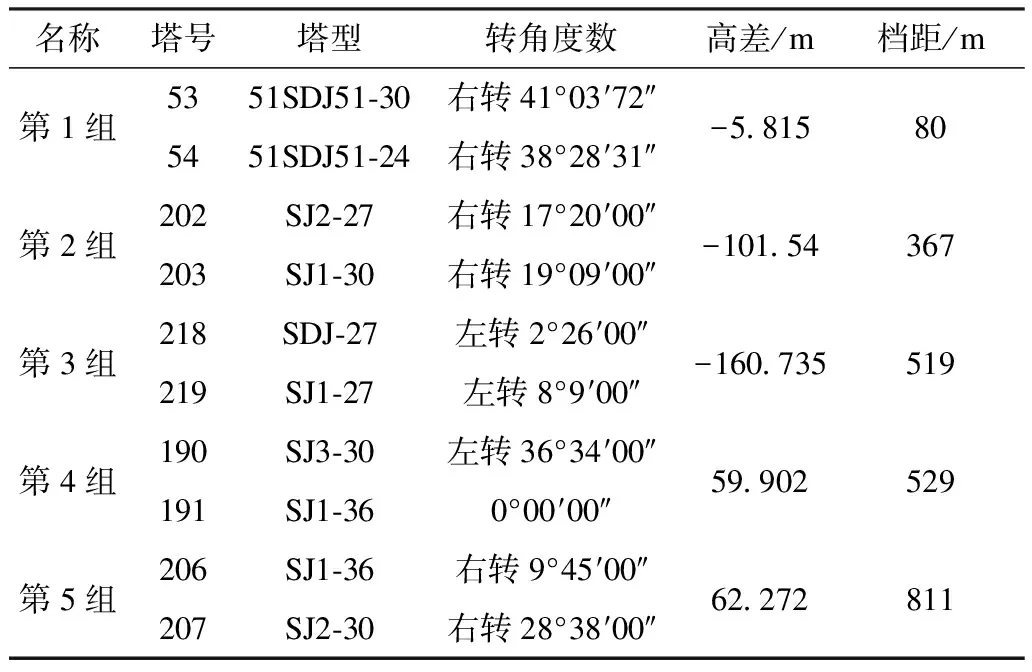
表5 线路参数表Tab.5 Line parameter table

3.2 实测结果对比及分析

实测结果对比如表6所示。通过比较分析可知，实测值基本上均小于传统方法和本文方法计算的数值，这是由施工误差造成；在安装相间间隔棒时，上相导线相较于中相导线人多质量大，导线弧垂下降得更多，使得上中相相间距减少，导致相间间隔棒调节板长度调得偏小，安装完成后下端导线往上偏移，如图8所示。相较于传统方法，本文方法算得的数值更接近实测值，误差比传统方法更小，最小误差为6 cm，最大误差为11 cm；传统方法算得的数值最小误差为22 cm，最大误差为151 cm，其中第5组2号相间间隔棒误差达到了151 cm，第3组1号相间间隔棒误差值达到了52 cm，误差较大情况在工程设计中应该引起重视。

从总体上分析可知，传统方法算得的长度均大于本文方法和实测值，这跟目前湖北投运的500 kV线路相间间隔棒长度偏长的情况一致，如图9所示。本文方法与实测值的误差由施工误差、相间间隔棒质量误差和现场测量误差造成。

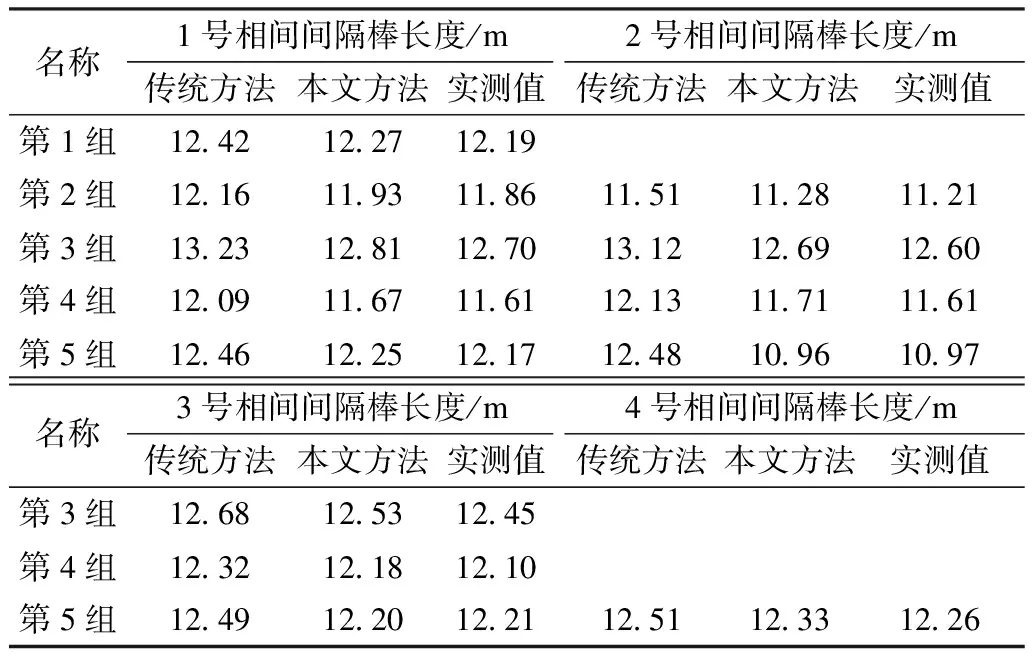
表6 实测结果对比表Tab.6 Comparison table of actual measurement results

图8 下端导线往上偏移Fig.8 Bottom wire offset upwards

图9 过长超出分裂导线间距Fig.9 Too long beyond the split wire spacing

4 结论

本文通过考虑集中荷载对弧垂的影响，提出了一种新的相间间隔棒长度计算方法。首先介绍了本文提出的计算方法，再通过工程算例将本文方法与传统方法对比分析，最后将实测值与本文方法和传统方法对比分析，得到如下结论。

1)传统方法未考虑集中荷载重量、数量和布置方式等因素的影响，导致相间间隔棒长度计算结果偏大，误差较大。本文方法均考虑了以上因素，计算结果误差较小，精度较高，验证了本文方法的准确性。

2)在档距小于300 m的情况下，传统方法产生的误差较小，基本可由调节板解决。在档距大于300 m情况下，传统方法误差较大，尤其在档距大于800 m时，2号相间间隔棒的计算长度已超出工程允许范围。

3)本文方法误差最大值为0.11 m，因此使用本文方法时调节板可以减少到±0.15 m。