基于暂态分层等值算法的UHVDC换流站短期可靠性评估
2022-06-09李生虎周慧敏陶帝文李璐璐
李生虎,周慧敏,陶帝文,李璐璐
(1. 合肥工业大学电气与自动化工程学院,合肥230009;2. 安徽省新能源利用与节能省级实验室,合肥230009)
0 引言
特高压直流(ultra-high voltage direct current, UHVDC)常用于远距离输电、异步互联等场景[1 - 4]。UHVDC电压等级高、容量大,其降额运行或停运,将导致电网功率缺额和频率下降,因此需要评估其可靠性[5 - 8]。
UHVDC换流站每极两个换流单元可独立运行。对换流站可靠性评估,可采用状态枚举、故障树、频率持续时间 (frequency and duration, F&D) 法、蒙特卡罗抽样等方法。文献[9 - 10]利用状态枚举法,研究了UHVDC换流阀、UHVDC/柔直系统可靠性。文献[11]使用故障树法评估换流阀可靠性。文献[12 - 14]利用蒙特卡罗抽样,分别计算海上高压直流配电网和微网可靠性。
上述研究都是评估UHVDC的长期可靠性。考虑元件故障和修复过程的指数衰减特性,一个初始完好元件安全运行200 h和20 000 h后,可靠性水平度肯定不同,长期可靠性评估不能反映当前运行下的短期可靠性。若短期可靠性评估中可靠性参数还受运行条件影响,则为运行可靠性,两者具有较强相关性。对于实际电网,重载、过电压、台风、高温、冰雪等运行条件,影响输电线路故障率和修复时间。文献[15 - 16]研究出力、元件故障和负荷波动随时间变化下对风电并网系统运行可靠性的影响。而换流站元件往往处于室内,受外界气象等因素影响不大,因此仅考虑时间推移的影响。对换流站短期可靠性分析,有利于估计换流站当前风险水平。尤其在元件失效后修复时,换流站可靠性增加,快速趋近稳态可用率,需要采用短时可靠性模型,来估计其可用率恢复程度。文献[17 - 21]采用设备时变故障率模型,评估电力系统短期风险。文献[22]采用动态故障树,评估主从控制微网短期可靠性。文献[23 - 24]使用时序蒙特卡罗法和半马尔可夫法,分别评估直流并网系统和UHVDC短时可靠性。文献[25]采用前推故障扩散算法,评估配网短期风险。文献[26 - 27]利用瞬时状态概率,评估单元件故障后电力系统短期可靠性,其中文献[26]忽略元件修复率影响,可能引起误差偏大。上述算法均是基于设备/电网完整状态空间模型,但是UHVDC换流站元件较多(本文元件数n=18),状态数最多为2n, 几乎不可能绘制状态空间图。需要根据设备结构和功能,将UHVDC换流站拆分成若干个子系统,分别建立状态空间模型,然后逐层向上等值,从而降低了状态空间维数,不能直接代入短期风险评估计算。
本文计及元件初始状态和UHVDC换流站结构,基于瞬时状态概率算法和分层等值过程,提出换流站暂态分层等值算法。基于换流站运行方式和多步转移过程,建立换流站瞬时状态空间模型,用于评估其短期可靠性。定义瞬时双极可用率、瞬时双极停运率、瞬时能量利用率、瞬时等效停运小时数,并计算其区间均值,拓展了换流站可靠性评估指标。
1 UHVDC换流站结构
UHVDC换流站一般采用双极双12脉换流器串联结构,由换流阀、换流变压器(简称换流变)、控制保护、交流滤波器、直流滤波器、平波电抗器等元件组成[28],如图1所示,其中一个换流单元连接6个换流变。根据可用容量,将换流站分为6种运行状态,分别为双极运行(100%)、3/4双极运行(75%)、单极运行(50%)、1/2双极(2×25%)、1/2单极运行(25%)和双极停运(0%)。
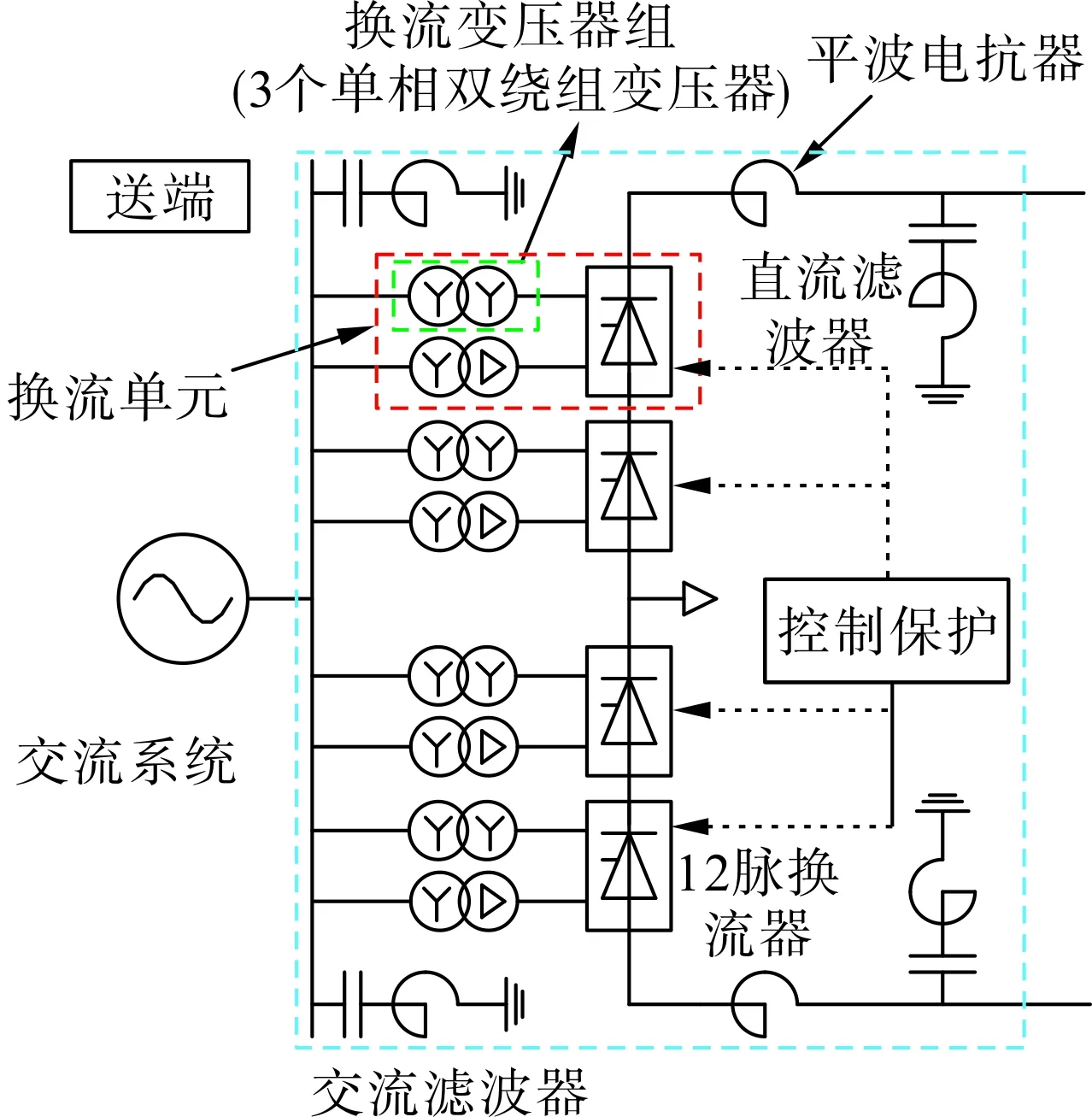
图1 UHVDC换流站结构Fig.1 Structure of converter station of UHVDC
2 UHVDC换流站短期可靠性评估
2.1 UHVDC换流站的暂态分层等值算法
UHVDC换流站瞬时状态特性是研究系统短期可靠性的重要指标。对于n状态可修复系统,若已知系统转移率矩阵的转置Φ和初始状态概率P(t0), 可得系统t时刻瞬时状态概率P(t)[29]。
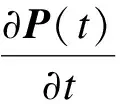
(1)
因Φ奇异,式(1)不能用于2.3节平均可靠性指标求解。不妨消去第n个状态,计算任意初始状态下瞬时状态概率。
(2)
式中:C为n-1维系数矩阵;上标Ct表示C和t的乘积;D为Φ的第n列前n-1行元素构成的列矩阵;φi,j为转移率矩阵的转置Φ的第i行第j列元素,即状态j至状态i的转移率;φi,n为状态n至状态i的转移率;ci,j为φi,j和φi,n之差;di,1为D的第i行第1列元素。
而换流站元件较多,计算系统转移率矩阵会出现维数灾难问题,故式(1)无法直接应用于换流站中。为解决维数过大问题,首先需将换流站状态空间降阶。本文基于F&D法[30],考虑系统任意时刻等值前后转移频率和状态概率不变原则,提出UHVDC换流站的暂态分层等值算法。
对于一个n状态系统,系统转移率只与元件自身参数有关。系统某时刻由状态i转移至状态j的转移频率fij(t)、 转移率aij和状态i概率Pi(t)满足以下关系:
fij(t)=aijPi(t)
(3)
将相同容量系统合并,根据等值前后状态间转移频率和对应状态概率相等原则得等值后某时刻状态I到状态J的转移频率f′IJ(t)及状态概率p′I(t)为:
(4)
(5)
为便于计算,将其转化成矩阵形式:
(6)
p′I(t)=XI(t)[pi(t)]
(7)
式中:XI(t)为n维行向量,当i∈XI(t)时,xi=1, 否则记为0;同理可得,当j∈XJ(t)时,xj=1, 否则记为0;[fij(t)]为等值前系统某时刻的转移率矩阵。
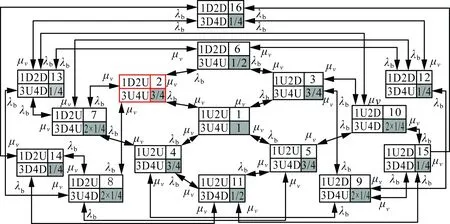
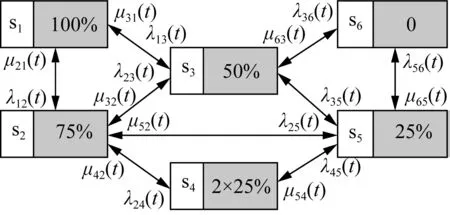
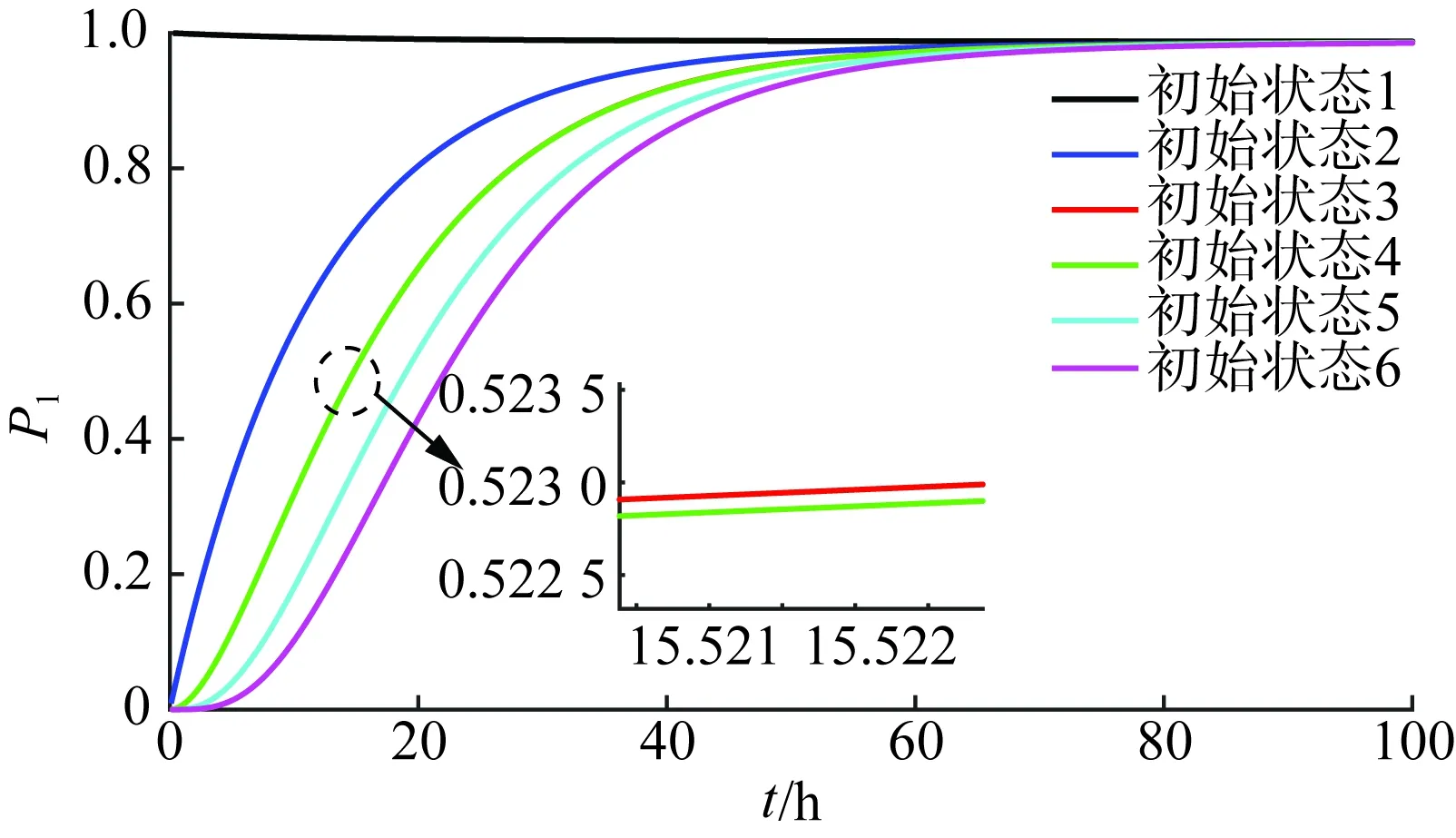
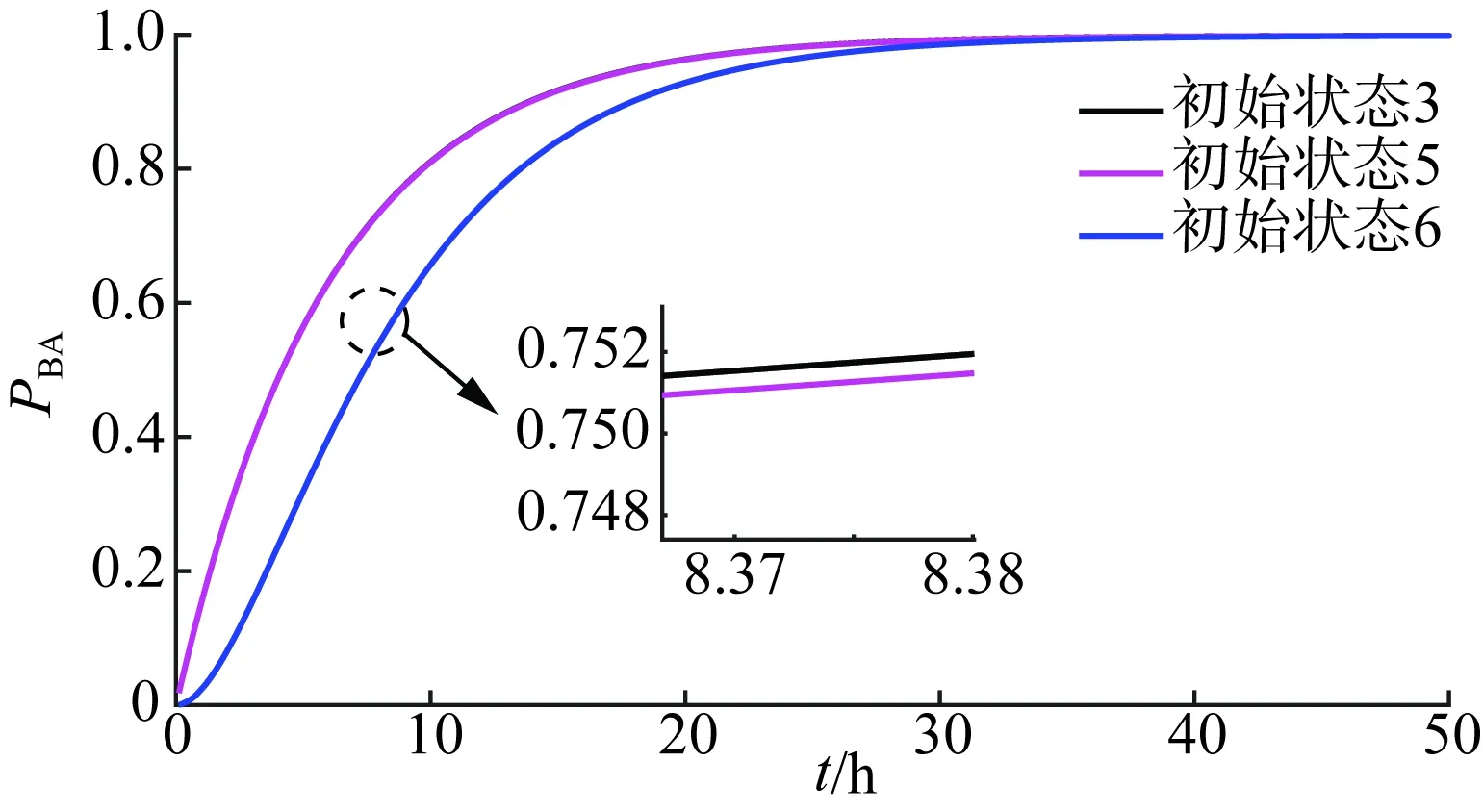
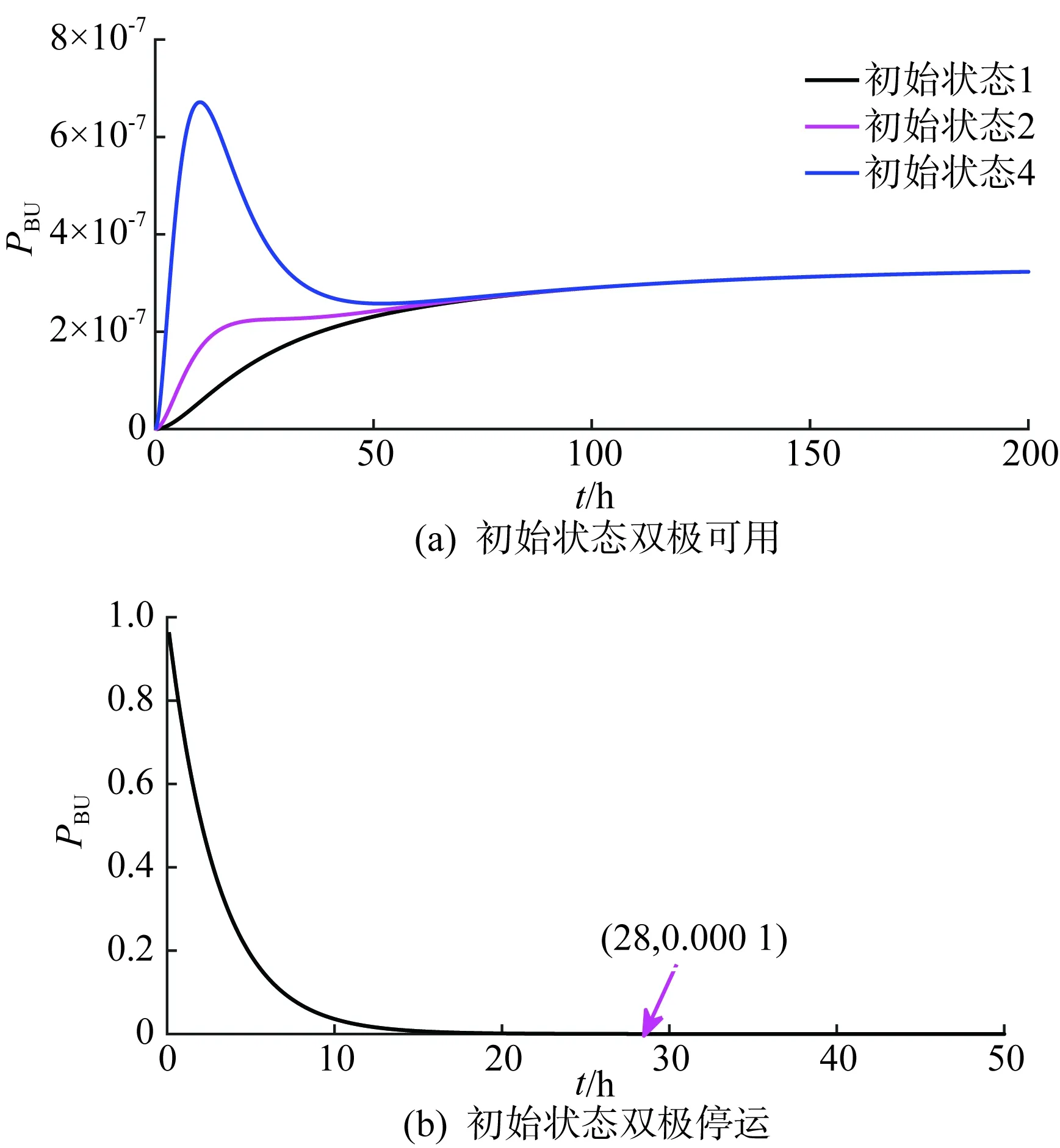
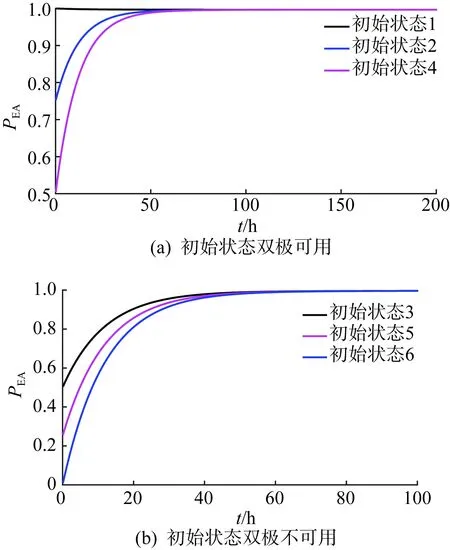
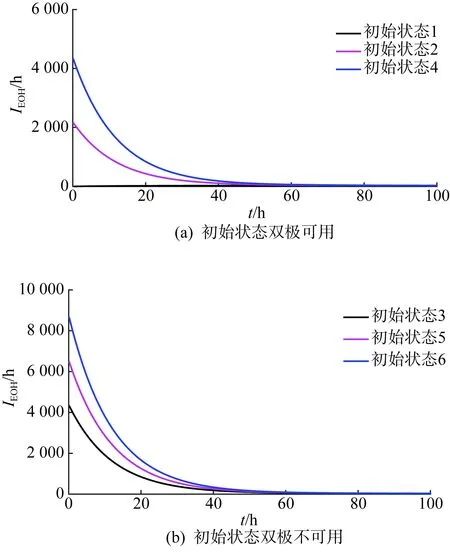
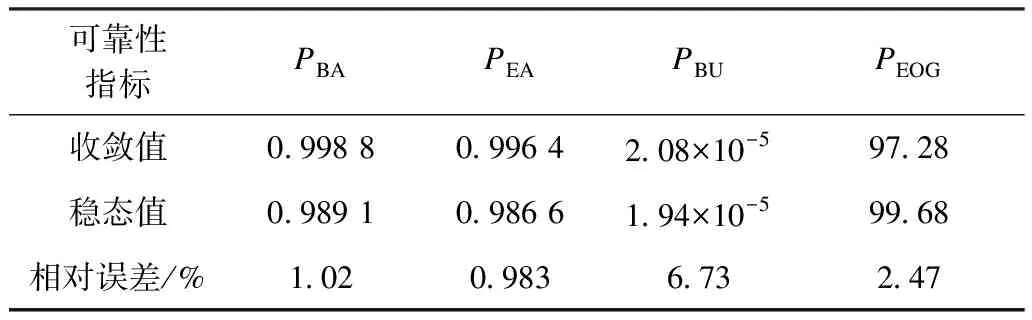
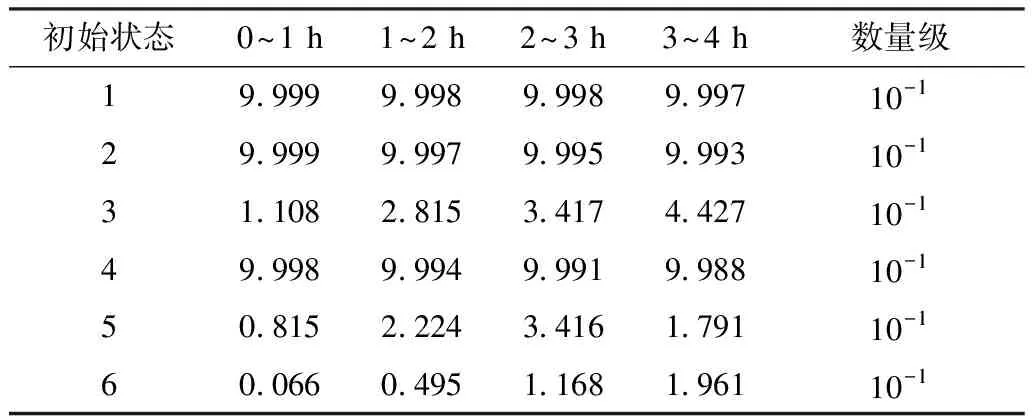
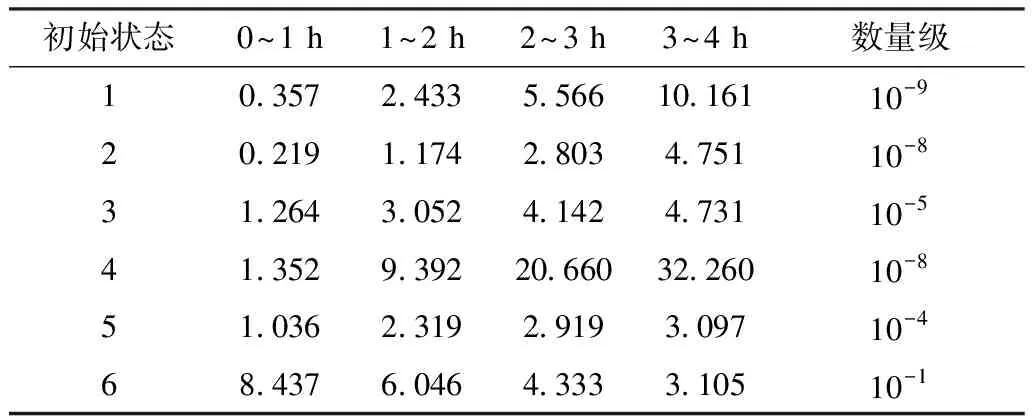
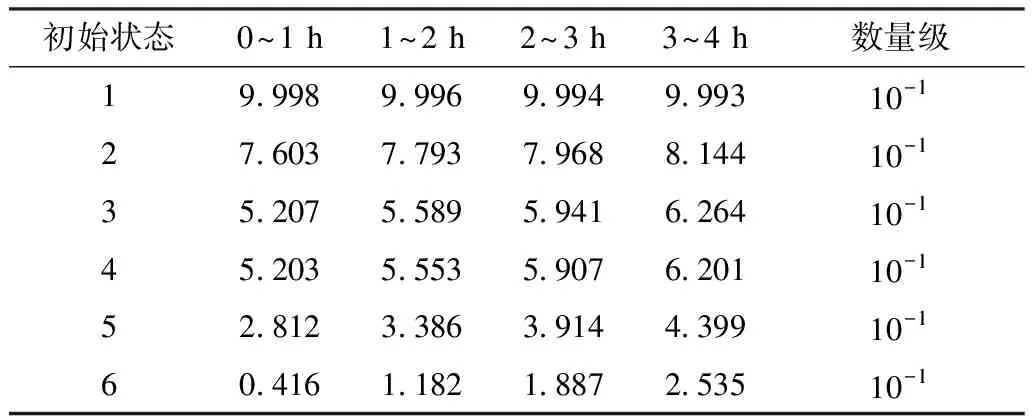
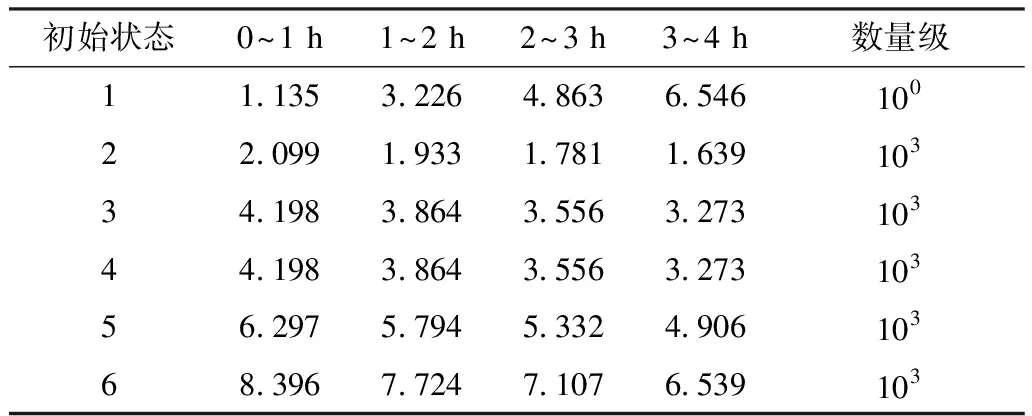
扩展到矩阵形式的时变系统中,系统由n状态等值为m状态(m F′(t)=MF(t)MT (8) P′(t)=MP(t) (9) 式中:M为m行n列常数矩阵,表征系统合并特征,M中每行具有相同容量的状态对应位置元素置1,其余元素置0;F(t)为转移频率矩阵;P(t)为状态概率矩阵;上标“′”代表系统等值后变量。 结合式(3)和式(8),可得等值后系统的时变转移频率矩阵为: F′(t)=MAP(t)MT (10) 式中A为转移率矩阵。 结合式(2)和式(9)可得系统等值后瞬时状态概率矩阵为: P′(t)=M{eCt[P(t0)+C-1D]-C-1D} (11) 将式(3)拓展成矩阵形式,可得等值后转移率矩阵计算关系,此时A′(t)具有时变特性。 (12) 将式(10)—(11)代入式(12)中得等值后系统转移率矩阵。 (13) 式(12)只能用于子系统的等值,而换流站的等值过程中还存在子系统间的组合与等值。不同于单个子系统的等值,组合后系统初始转移率矩阵具有时变特性,即对应等值后系统转移率矩阵中C和D均为变量。 建立换流站等值状态空间,分为3个步骤。首先将换流站按照功能划分为换流桥、换流变、控制保护、交流滤波器等子系统,基于元件参数建立各子系统初始状态空间模型。其次根据暂态分层等值算法,在考虑元件初始状态的前提下分别进行子系统的暂态等值,降低状态空间维数,建立各子系统的时变状态空间模型。最后将等值后的子系统两两组合最终得到换流站的时变状态空间模型。 建立子系统初始状态空间模型,需考虑元件的状态转移过程。以换流桥为例,选定换流阀为基本单元,建立初始16状态的状态空间模型,如图2所示。此时系统转移率矩阵仅与元件本身参数有关,D表示换流阀故障,U表示正常运行。 图2 换流桥状态空间Fig.2 State space of converter bridge 建立子系统的时变状态空间模型,需先确定系统初始状态。假设系统初始时仅有一个换流阀故障,不妨设初始时换流桥处于状态2,得系统初始状态概率P0。 按照相同容量状态合并原则可列写M矩阵,根据式(13)得等值后换流桥系统6状态的时变状态空间模型如图3所示,即转移率本身和评估时刻有关。同理可得其他子系统的等值时变状态空间模型和时变转移率矩阵,这里不再赘述。 图3 换流桥时变等值状态空间模型Fig.3 Equivalent state space model of converter bridge with time 以上模型建立中未考虑元件存在备用情况,不同元件备用,对换流站状态空间建模影响不同。换流桥子系统中4个12脉换流阀,一个12脉换流阀是最小的功能单元,当任一阀臂故障时,会使整个12脉换流阀停运。设置备用时4个12脉换流阀共用备用阀,每增加一个备用阀,换流桥状态空间将增加6个状态。换流变子系统中共有24个换流变, 1个12脉换流阀上分别连接6个换流变(3个Y/Y型和3个Y/Δ型),当一个换流变故障后,其余5个停运。这24个换流变共同备用,但需区分变压器类型,每增加一个Y/Y(Y/Δ)型备用变压器,状态空间将增加6个状态。交流滤波子系统中,每极有两组交流滤波器组(常见滤除谐波12n±1和6n±1), 两组可以共用备用。增加某一个滤波器备用,状态空间将增加3个状态。元件备用数量只影响等值前的状态空间数量和常数矩阵M, 对等值后状态空间数量无影响。以换流桥为例,增加一个备用阀的状态空间模型如图4所示。S表示待安装状态。 图4 换流桥的状态空间(1备用)Fig.4 State space of converter bridge with 1 spare 为得到换流站的时变状态空间模型,还需进行子系统间的组合与等值。以等值换流桥和等值换流变的组合为例,状态空间模型如图5所示。图中转移率为换流桥和换流站子系统等值后的时变转移率矩阵得来,与图2有所区别。 图5 等值换流桥与换流变组合时变状态空间Fig.5 State space of converter bridge and transformers 组合系统初始状态与两子系统元件初始状态均有关,故在进行子系统间暂态等值前需判断系统初始状态,图5中标出初始时组合系统处于状态2。根据2.1节暂态等值算法可得等值后系统时变6状态空间模型,与图3结构相同,这里不再赘述。 在换流站的多次等值过程中,每次等值均需判定系统初始状态。按上述暂态分层等值算法和多步转移等值过程,可得换流站等值后6状态瞬时状态空间模型和瞬时状态概率。等值过程如图6所示。 图6 UHVDC换流站暂态分层等值Fig.6 Instantaneous hierarchical equivalence of UHVDC converter stations 在给定初始状态下,基于上述算法和等值过程可得换流站任意时刻任意状态的状态概率。为量化换流站的短期可靠性变化情况,本文基于稳态可靠性指标,如双极可用率、双极停运率、能量利用率和等效停运小时数[31 - 32],引入用于评估HVDC短期可靠性的指标。定义瞬时双极停运率PBU(t)和瞬时双极可用率PBA(t), 评估系统在不同初始条件下完全故障和可用概率;定义瞬时能量可用率PEA(t)和实时等效停运小时数IEOH(t)指标,评估系统在不同初始条件下能量利用效率随时间变化关系。 (14) PBA(t)=P1(t)+P2(t)+P4(t) (15) (16) (17) 式中Pi(t)为状态i在t时刻的概率。 上述指标反映换流站出现不同程度故障后可靠性随时间变化情况,有利于估计换流站当前风险水平,并做出对应措施。 实际工程中一般选择几个特定时刻评估系统风险,这可能会高估或低估系统的可靠性水平,故使用平均状态概率[29,33]。不考虑换流变系统的历史状态,取评估起始点t1, 选定时间段T=[t1,t2], 求解T内的系统各状态平均概率为: (18) 因Φ不可逆,使用改进瞬时状态概率算法代入上式中。定义平均双极停运率、平均双极可用率、平均能量可用率和平均等效停运小时数指标,如式(19)—(22)所示,研究系统在T内的可靠性,同时对比研究换流站在不同时期内的可靠性变化情况。式中顶标“—”代表该变量的区间均值。 (19) (20) (21) (22) 为验证所提算法的正确性和效率,以3个元件并联的小系统为例,在相同时刻,以完整状态空间模型为基准,分别计算系统瞬时状态概率,验证算法分层等值算法准确性。 给定λ1=0.01 次/a,λ2=0.05 次/a,λ3=0.02次/a,μ1=0.25 次/h,μ2=0.3 次/h,μ3=0.3次/h。建立验证系统的完整状态空间模型如图7所示。图中,U表示正常运行,D表示元件故障。 图7 8状态系统完整状态空间Fig.7 Complete state space of 8 states system 采用暂态分层等值算法时,考虑将元件1和元件2看作一个子系统,再与元件3合并。等值过程如图8所示。 图8 8状态系统等值过程Fig.8 Equivalent process of 8 states system 假设系统初始时元件1故障(处于状态2),按照图7和图8的状态空间可分别计算两种算法下系统状态1的瞬时状态概率,如图9所示。选定评估时刻t=20, 比较该时刻下各方法所得系统状态1概率和所需计算时间,如表1所示。 采用不同的可靠性评估方法,P1的相对误差为0.02%,误差较小,证明了本文所提方法的正确性。在计算时间的比较上,本文所提方法仅为现有算法的33.9%,显然效率更高。这是因为本文提出的暂态分层等值方法降低了状态空间维数,降低了计算的复杂程度,具有更高的计算效率。 图9 不同方法下P1随时间变化Fig.9 P1 change with time under different methods 表1 不同方法下短期可靠性评估比较Tab.1 Comparison of short-term reliability assessment under different methods 稳态可靠性参数是瞬时状态概率可靠性参数的区间均值,受天气等极端条件影响较大,在极端恶劣条件下,元件故障率上升修复率不变;且轻载和重载时元件故障率存在差异。本文的研究对象为换流站,受天气影响不大,主要受运行方式影响,故使用长期规划下的元件可靠性参数进行研究,参数取自文献[34],具体如表2所示。 表2 UHVDC换流站原始参数Tab.2 Original parameters of UHVDC converter stations 根据第2节所述算法和等值过程,可得换流站短期可靠性的计算结果。 3.2.1 等值前后的转移率矩阵 以换流桥等值前后转移率矩阵计算为例,图2给出换流桥的状态空间有16个状态,故转移率矩阵A为16阶方阵,矩阵A中元素aij(i≠j)表示状态i转移到状态j的转移率,在换流桥子系统中表现为换流阀的故障和修复对应的故障率和修复率。主对角线上元素aii为该行所有元素之和的相反数。换流桥等值前的转移率矩阵A为常数矩阵见式(23)。 设置换流桥初始处于状态2(一个换流器阀故障,运行容量为75%),假设取t=20, 根据图3和式(13)可得出该时刻下等值后换流站转移率矩阵为: (24) 3.2.2 系统瞬时状态概率 本文以换流站正常运行(状态1)为例,计算系统不同初始状态下的状态1概率(P1)随时间变化关系,如图10所示。6种初始状态分别为换流站无故障(运行容量100%)、单个换流阀故障(运行容量75%)、单极的两个换流阀故障(运行容量50%)、两极均有一个换流阀故障(运行容量25%×2)、3个换流阀故障(运行容量25%)、4个换流阀均故障(运行容量0)。 在不同故障情况下,系统状态1概率均逐渐增加并收敛至稳态值。这表明在元件故障修复时,时间越长,元件可用率修复程度越高。当系统初始容量均为50%时(图10中初始状态3和4),P1随时间变化趋势仅有微小差异可忽略,可认为在故障元件相同时,系统状态1的瞬时状态概率与元件故障位置无关。 图10 UHVDC换流站P1随时间变化Fig.10 P1 change with time in UHVDC converter station 3.2.3 系统瞬时可靠性指标 根据2.3节瞬时可靠性指标定义,计算换流站瞬时双极可用率随时间变化关系如图11所示。 图11 PBA(t)随时间变化Fig.11 PBA(t) change with time 若初始时换流站双极不可用(初始状态3、5、6),系统双极可用率也会随时间逐渐增加并收敛至稳态值。与图10相比,收敛速度更快,这表明当系统发生不同程度故障后,会先迅速修复至双极可用。 为研究系统不同故障情况下停运概率随时间变化关系,绘制双极停运率随时间变化关系曲线。 图12(a)中可看出,当换流站初始双极可用时,其双极停运率虽存在短时激增但值一直接近于0。图12(b)可以看出当系统发生不严重故障造成的初始停运时,通过元件自身修复特性,双极停运率迅速降低至接近0。 为验证系统不同情况下的能量利用效率随时间变化关系,绘制PEA和IEOH随时间变化曲线,如图13—14。在相同时刻下,换流站初始容量越大,系统能量利用率越高。在任何情况下,系统均有一定的自身调节能力,提高系统能量利用效率。 图12 PBU(t)随时间变化Fig.12 PBU(t) change with time 图13 PBA(t)随时间变化Fig.13 PBA(t) change with time 图14 IEOH(t)随时间变化Fig.14 IEOH(t) change with time 换流站可靠性指标随时间变化均收敛至某一稳态值,分别计算可靠性指标收敛值与长期可靠性结果下的稳态值,比较两者差异如表3所示。各指标的收敛值与稳态值差异较小,这也验证了短期可靠性评估下指标的正确性。 表3 不同方法下可靠性指标比较Tab.3 Comparison of reliability index with different methods 3.2.4 评估周期内可靠性指标 取短期风险评估周期为1 h,计算各时段内系统的可靠性指标如表4—7,并得出以下结论。 表4 评估周期内平均双极可用率Tab.4 Average bipolar availability within the evaluation period 表5 评估周期内双极停运率Tab.5 Bipolar outage rate within the evaluation period 表6 评估周期内平均能量利用率Tab.6 Average energy availability within the evaluation period 表7 评估周期内平均等效停运小时数Tab.7 Average equivalent outage hours within the evaluation period 1)当换流站初始状态双极可用(状态1、2、4)时,系统短时间内的平均双极可用概率和能量利用率接近1且波动幅度较小,可近似使用稳态可靠性分析。当系统初始状态处于单极可用状态时(状态3、5),不同时间段下的平均双极可用率和双极停运率差异明显,且随时间推移逐渐增大。 2)换流站除状态1外,系统的平均能量利用率和等效停运小时数在不同时间区间差异明显,故在实际工程,需缩短评估周期。 为简化UHVDC换流站的短期可靠性评估,本文基于瞬时状态概率算法和分层等值过程提出暂态分层等值算法,建立换流站的等值状态空间模型和瞬时状态概率模型,研究系统在不同初始状态下的短期可靠性。引入瞬时双极可用率、瞬时双极停运率等指标评估系统可靠性随时间变化。考虑使用瞬时状态概率可能出现高估或低估系统可靠性的情况,以故障后的4 h为例,以1 h为评估区间计算其平均双极停运率和双极可用概率等指标,得到结论如下。 1)当UHVDC换流站系统发生不严重故障时(仅有一个或几个元件故障),系统可通过自身修复特性在故障发生后的一段时间内恢复正常运行。当换流站初始处于较低容量运行时,系统会随时间变化逐渐提高运行容量。 2)当换流站发生双极停运故障时,系统会迅速修复,降低双极停运概率。虽换流站双极停运对系统影响较大,但实际工程中系统发生双极停运概率极低。 3)本文在评估换流站短期可靠性时,只考虑系统中换流桥发生单元件或多元件故障的情况。实际工程中存在多种故障可能性,当故障程度较大时,换流站的短期可靠性变化还需进行深入研究。2.2 UHVDC换流站时变状态空间等值模型
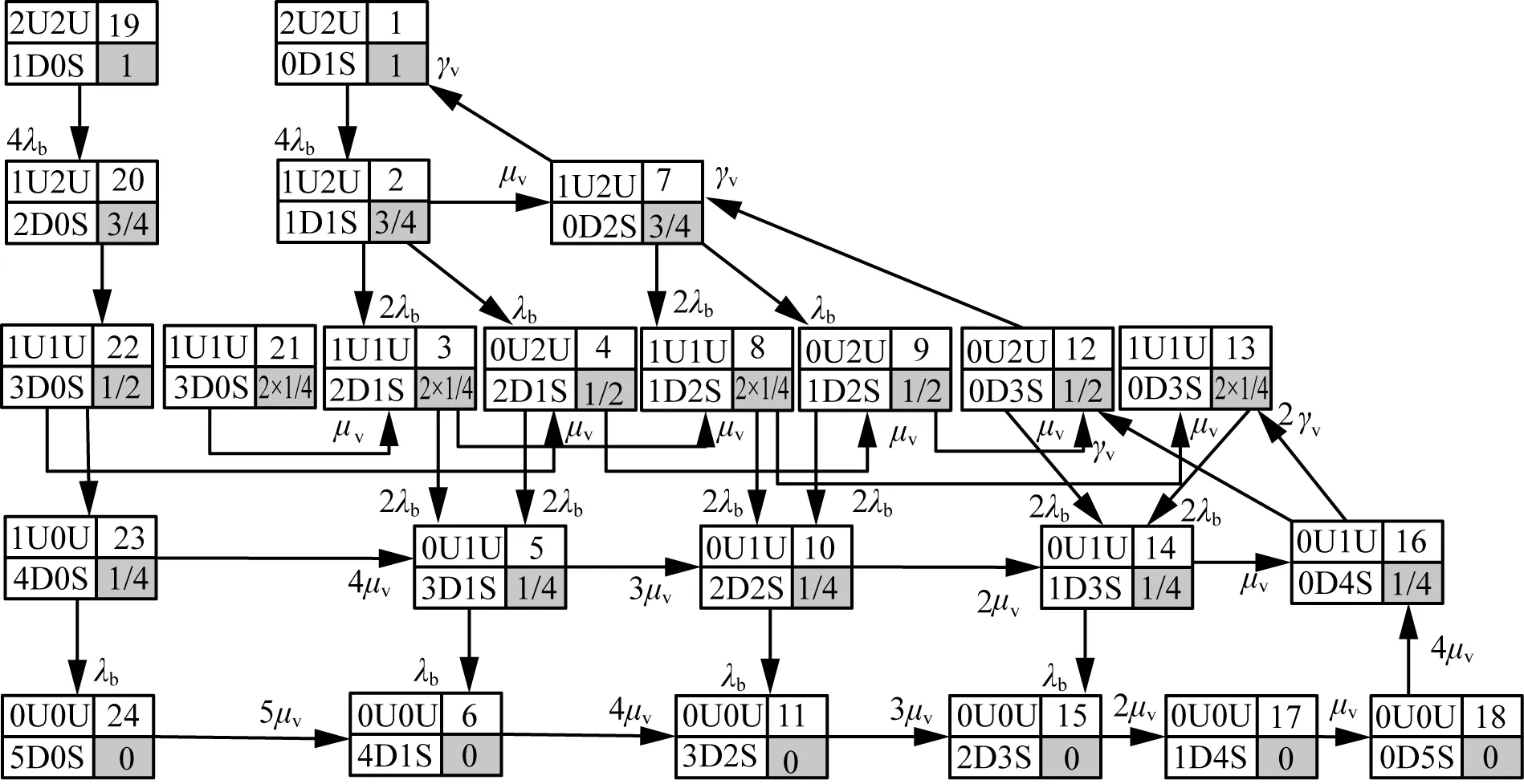
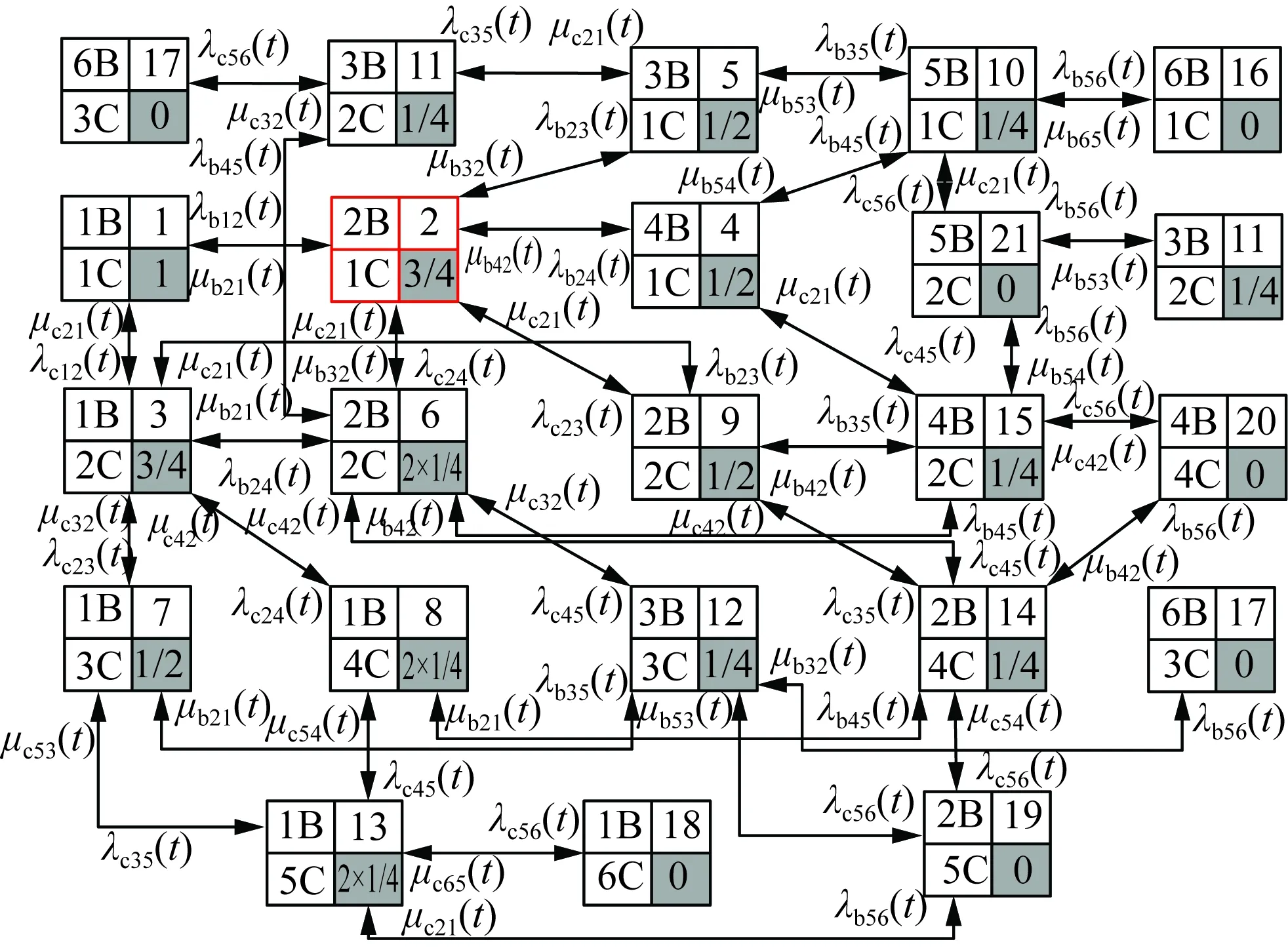
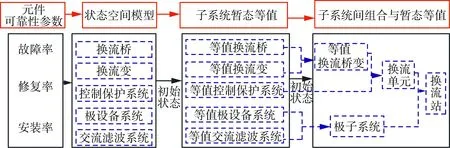
2.3 UHVDC换流站短期可靠性指标
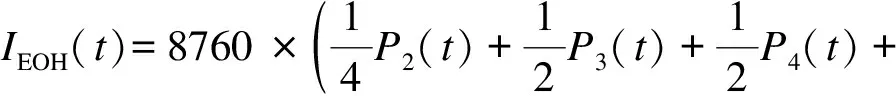
3 算例分析
3.1 暂态分层等值算法检验
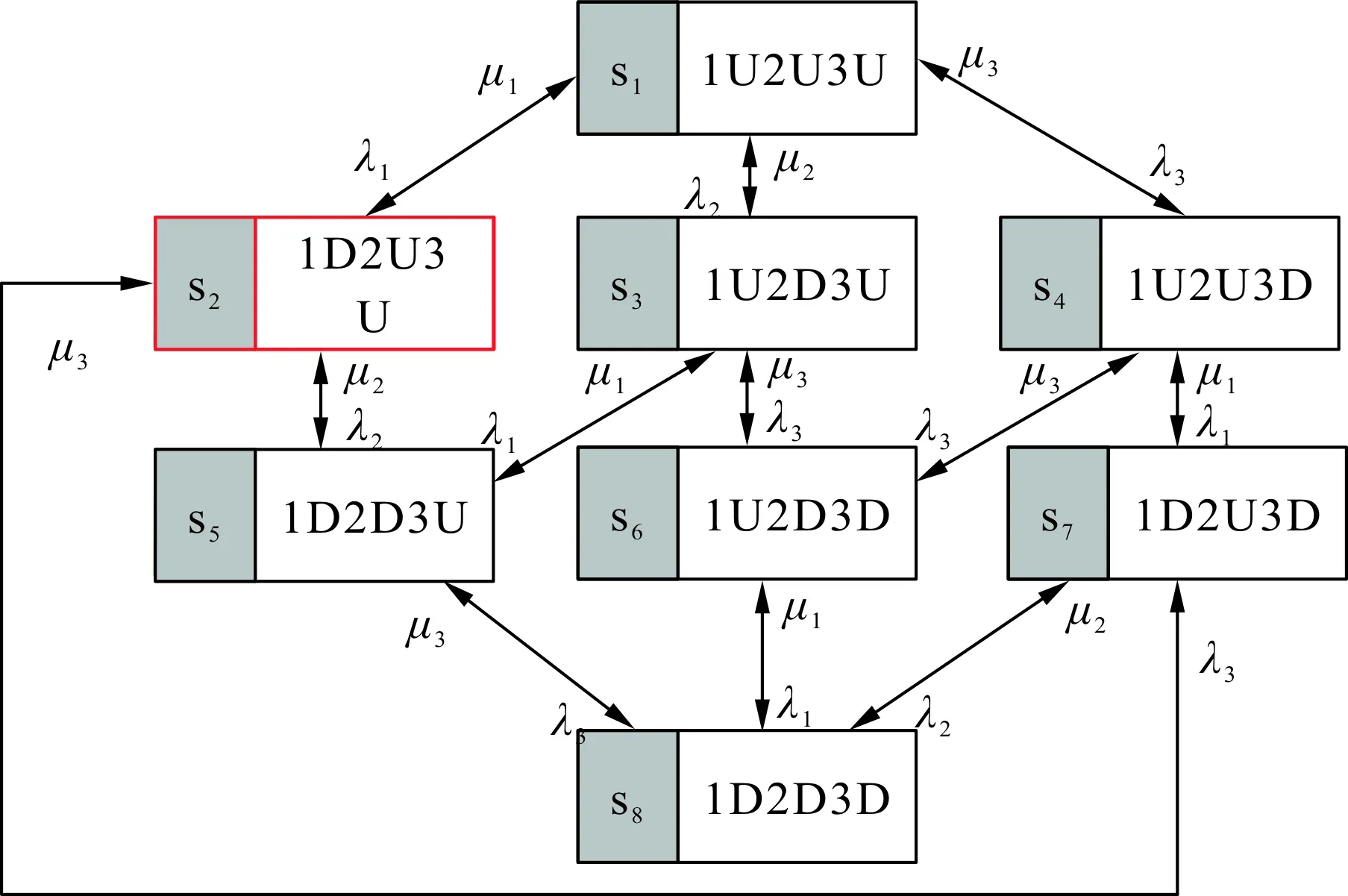
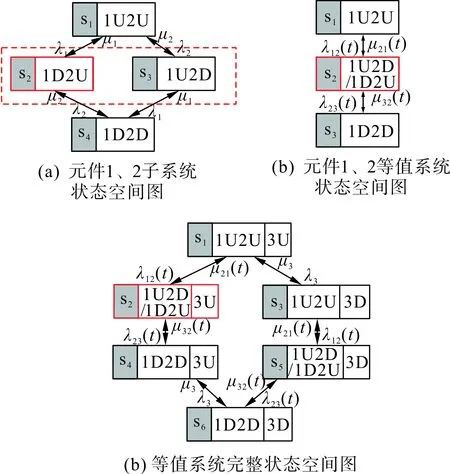
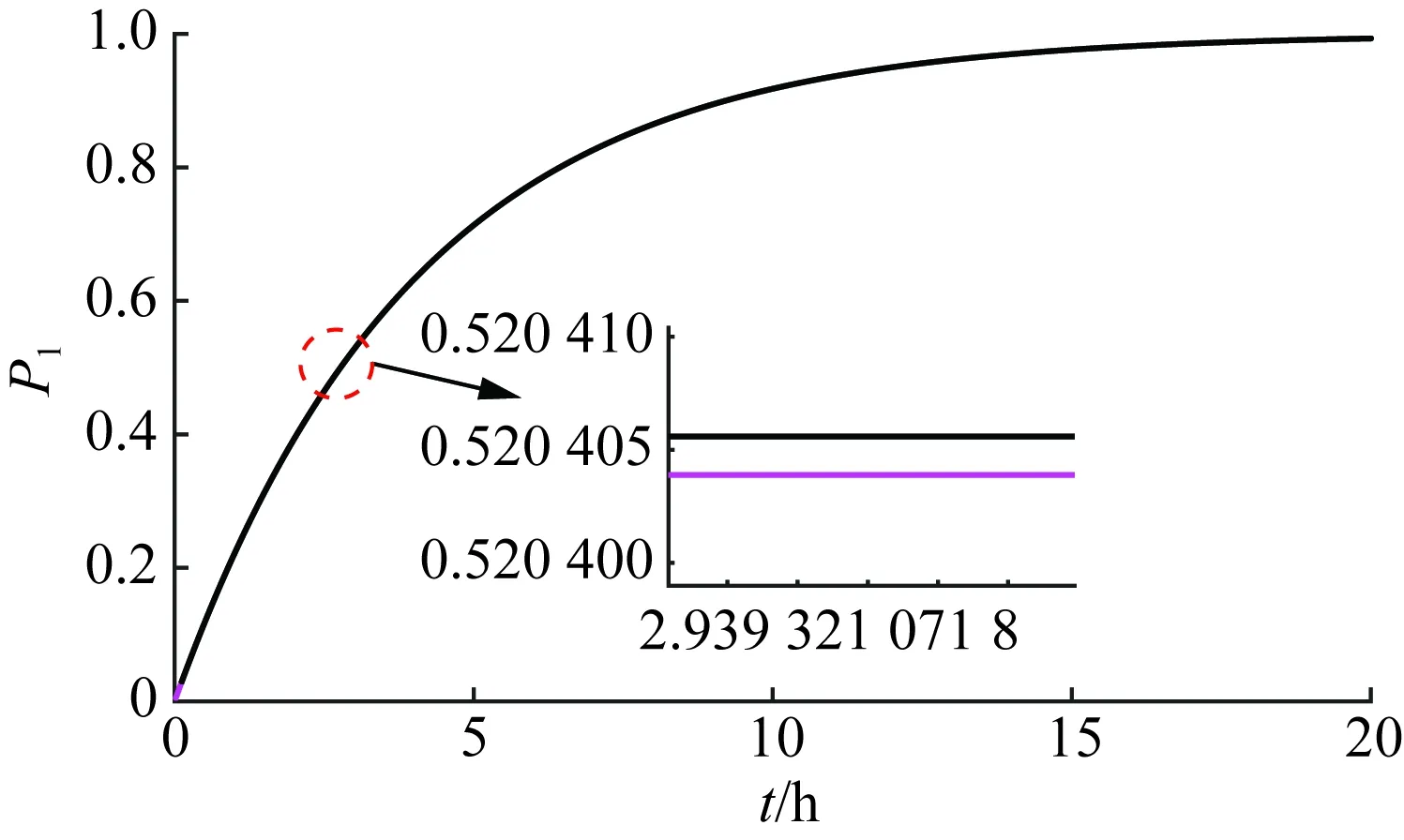

3.2 算法有效性分析
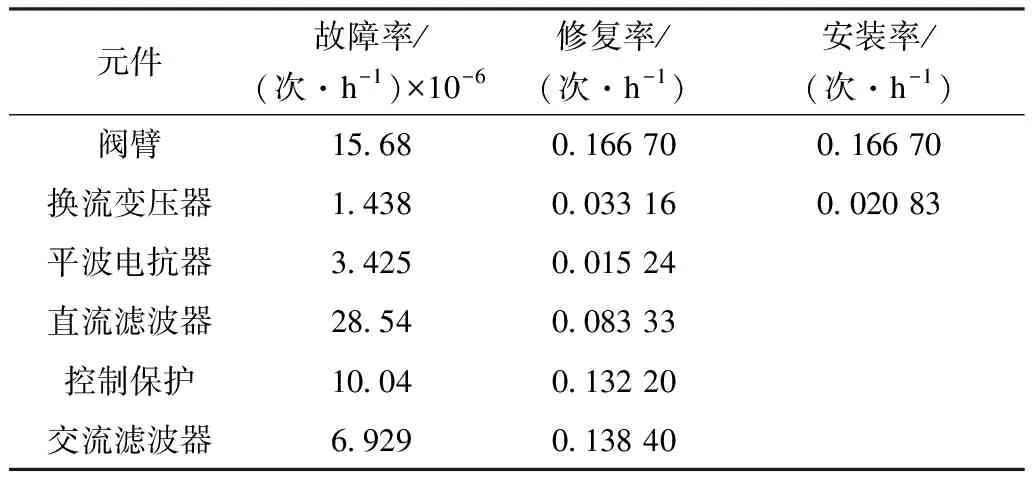
4 结论
