多并网逆变器并联运行的谐振抑制策略

王毅，高爱杰，胡楠，曹添，郭锐，杨龙月

(1. 国网江苏省电力有限公司泗洪县供电分公司，江苏 宿迁223800；2. 中国矿业大学电气与动力工程学院，江苏 徐州221008；3.国网浙江省电力有限公司检修分公司，杭州311200)

0 引言

随着我国持续推进能源转型战略，以太阳能等新能源为代表的分布式发电系统在电力系统中的占比不断提升[1]。一方面，长距离输电线、变压器漏感等原因使得电网逐渐呈弱电网特性，大规模光伏发电系统、静止无功发生器、变频器等电力电子设备的接入易引发系统振荡等问题[2]。另一方面，LCL型并网逆变器因其具有较强的滤波能力在工程中得到广泛应用[3 - 4]，但在弱电网环境下其自身存在谐振问题。弱电网下由于电网阻抗的存在，多台逆变器并联运行时各逆变器间彼此耦合[5 - 6]，导致整个系统发生谐振，且谐振频率通常随并联台数的增加逐步由高频变为低频，增加了控制系统的难度[7 - 8]。

针对多台逆变器并联运行时的谐振机理与特性，国内外学者已开展相关研究。文献[9]应用模态分析法和计算谐振参与因子评估系统谐振状态，解析了多逆变器并联系统的谐振特性规律及其交互特性。文献[10]通过诺顿等效推导多机并联系统输出阻抗模型，结合阻抗特性阐明了多机系统耦合原因与谐振机理。基于上述研究，为解决多机并联系统的谐振问题，现有抑制弱电网下逆变器谐振问题的策略主要集中于调整逆变器输出阻抗或公共耦合点(point of common coupling，PCC)处的电网等效阻抗，对应设计控制方案从而抑制谐振[11 - 13]。文献[14]提出串并联阻抗校正法，引入串联和并联虚拟阻抗分别实现提升逆变器闭环输出阻抗的相位与幅值。文献[15]提出通过改变电容电流反馈系数调节逆变器闭环输出阻抗频率响应的策略，该策略使逆变器满足稳定判据。文献[16]提出在PCC点处并联接入有源电容变换器的方法，通过在PCC点并入可调虚拟电容动态调整电网的等效阻抗。文献[17]提出一种将RC支路并入PCC点的谐振抑制策略，调整电网等效阻抗输出频率特性来抑制逆变器的谐振，但当多逆变器并联时无法采用该策略。文献[18]提出有源谐波电导法，通过加入虚拟电导吸收低次谐波电流实现对谐波电流的抑制。文献[19]通过带通滤波器在谐振频率处构建虚拟导纳，以此实现抑制谐振，但未阐明带通滤波器的具体设计方法。

本文基于多逆变器并联的诺顿等效模型分析得出多逆变器并联运行的Nyquist稳定判据，考虑由外引入虚拟导纳，提出了通过基波陷波器向PCC点加入虚拟等效导纳的整机谐振抑制策略，并搭建仿真模型和实验平台验证了所提多并网逆变器并联运行的谐振抑制策略的有效性。

1 LCL并网逆变器闭环输出阻抗模型

含电网电压前馈控制单元的LCL型并网逆变器如图1所示。图中Vin为直流侧的逆变器输入电压，L1为逆变器侧等效电感，L2为网侧等效电感，C为滤波电容，Vg为电网电压，Hi1、Hi2、Hv依次表示采样电容电流、并网电流、电网电压的反馈系数，PLL为检测同步信息的锁相环，Gi(s)为电流调节器，I*为输出电流参考值，Gff(s)为电网电压前馈控制单元。为提高本文研究的适用性，Gff(s)选取电网电压比例前馈控制。

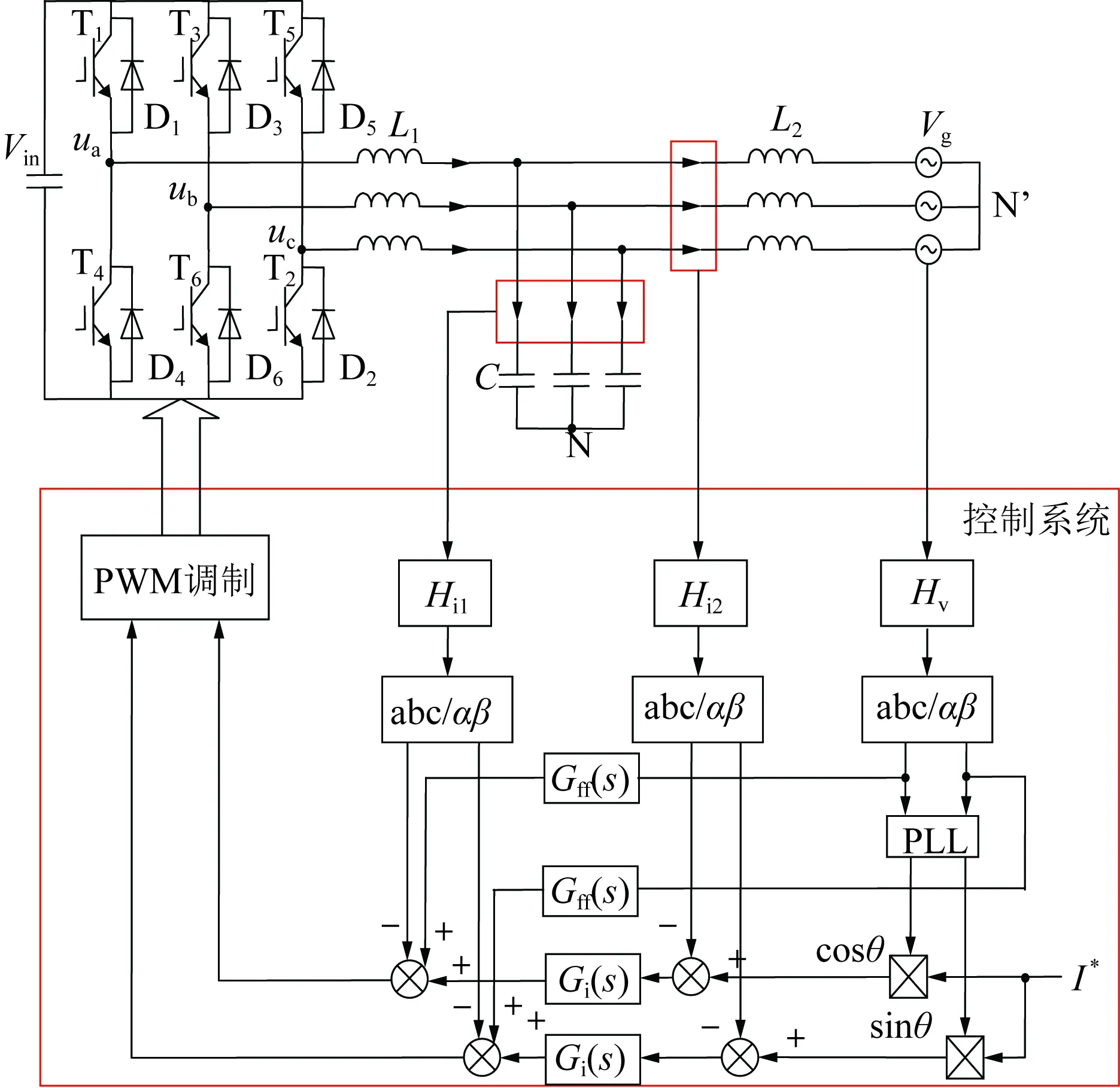
图1 LCL型并网逆变器原理图Fig.1 Schematic diagram of the LCL grid-connected inverter

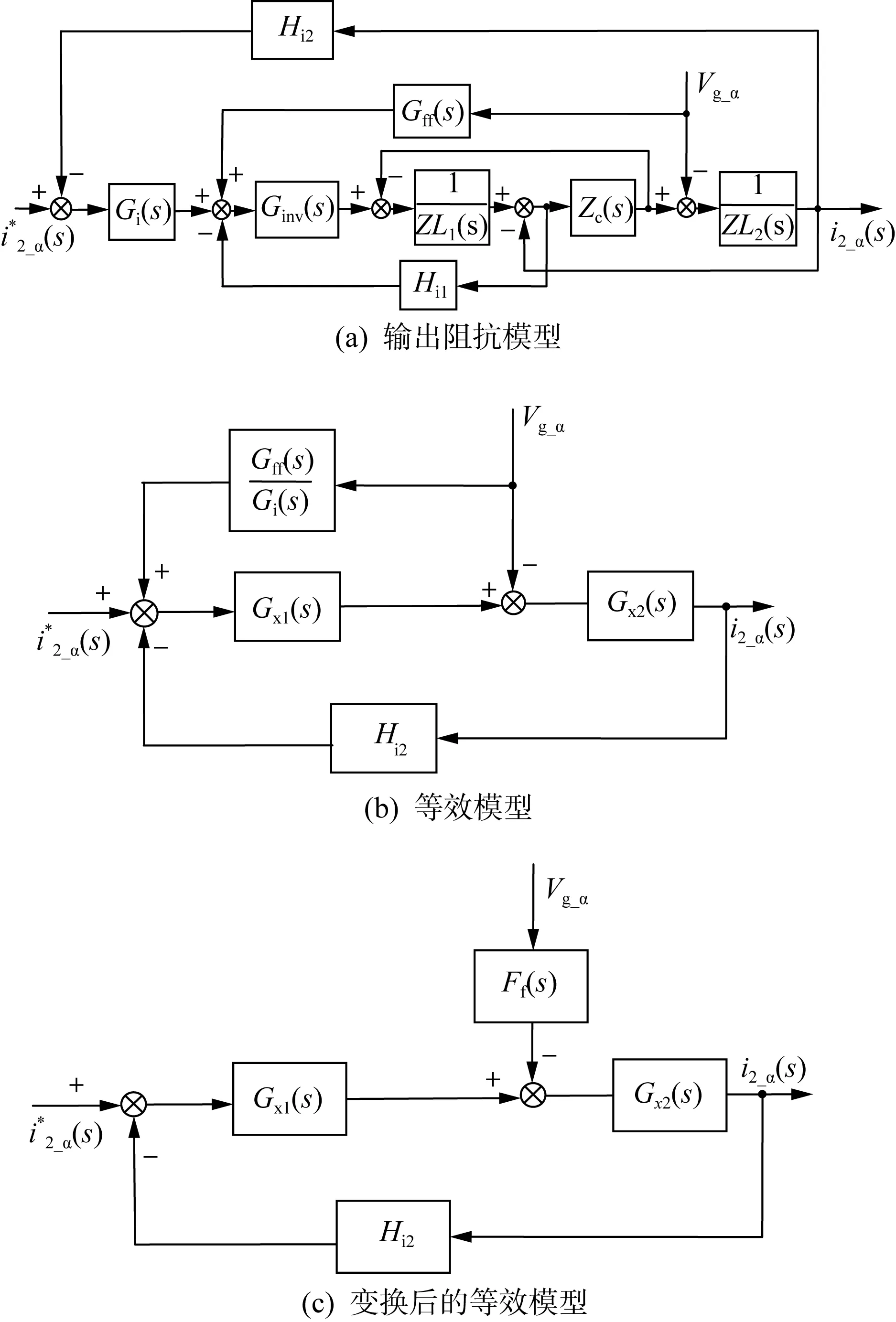
图2 α轴上逆变器输出阻抗模型推导过程Fig.2 Derivation process of the inverter output impedance model on α-axis

为简化分析，仅在α轴上分析输出阻抗模型，如图2所示。图2(a)中Vg_α为坐标变换后网侧电压在α轴上的分量，Ginv(s)为逆变桥的等效传递函数，考虑数字控制延时带来的影响，其表达式为[20]：

(1)

式中：Vtri为载波幅值；Ts为采样周期；Kpwm为调制信号至逆变桥输出电压的传递函数的增益值，即Vin/(2Vtri)[21]。

为简化模型，前移Gff(s)的比较点至Gi(s)输入端可将图2(a)等效为图2(b)，图中扰动信号前传递函数Gx1(s)与扰动信号后传递函数Gx2(s)表达式为：

(2)

(3)

在图2(b)中，将电网电压前馈点后移至Gx1(s)的输出端，可将图2(b)等效为图2(c)，图中Ff(s)表示等效变换后的含电网电压比例前馈的控制环节，Ff(s)表达式为：

(4)

分析图2(c)可得逆变器输出电流为：

(5)

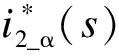
(6)

联立式(1)—(4)、式(6)，可得闭环输出阻抗：

Zo(s)=[s3L1L2C+s2L2CHi1Ginv(s)+s(L1+L2)+

Gi(s)Hi2Ginv(s)]/[s2L1C+sCHi1Ginv(s)+

1-Gff(s)HvGinv(s)]

(7)

其中电网电压比例前馈项如下，详见文献[22]。

(8)

2 多机并联系统谐振特性及稳定性分析

2.1 多机并联系统谐振特性分析

通过戴维南定理将逆变器多机并联运行开环等效电路表示为图3。

图3中，Goci(s)和Zoci(s)分别为第i台逆变器的输出电压开环增益与输出阻抗，其表达式为：

(9)

(10)

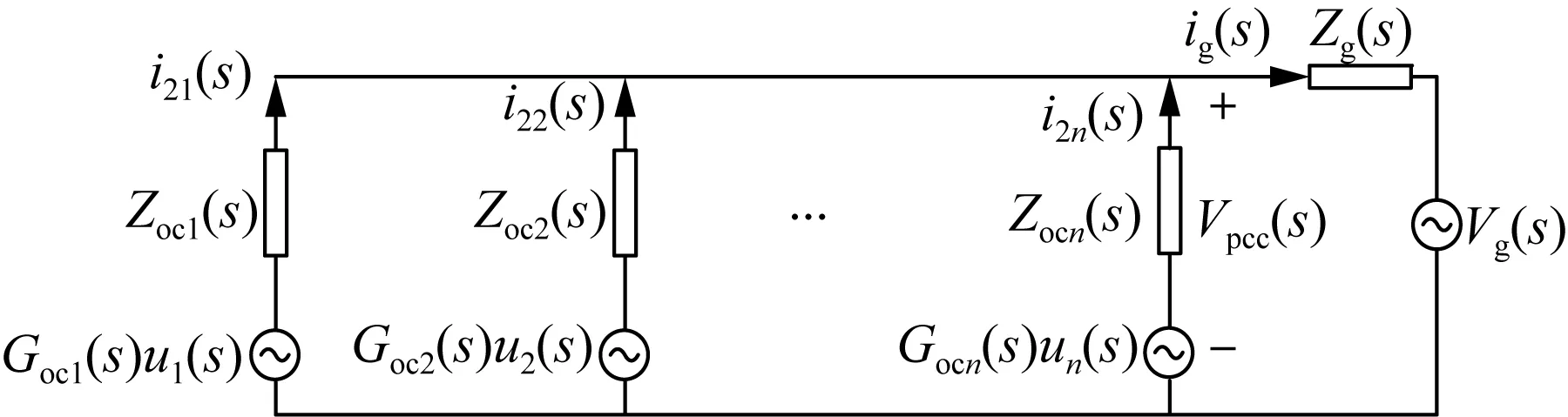
图3 多机并联系统开环戴维南等效电路Fig.3 Open-loop Thevenin equivalent circuit of multi-machine parallel system

由叠加定理得开环多机并联系统中第i台逆变器输出电流为：

y1(s)Vg(s)

(11)

其中G11(s)、G12(s)、y1(s)的表达式分别为：

(12)

(13)

(14)

强电网情况下，电网等效阻抗Zg(s)=Lgs=0，联立式(11)—(14)得强电网下第i台逆变器输出电流为：

i′2i(s)=G11(s)ui(s)+y1(s)Vg(s)

(15)

分析式(15)可知，此时逆变器输出电流由电网电压Vg(s)与其自身输出电压ui(s)决定，不受其余逆变器输出电压的影响。

在弱电网环境下，Zg(s)=Lgs≠0，由式(12)—(14)可知，此时逆变器输出电流受其余逆变器输出电压影响，各逆变器间存在耦合，且多机系统的耦合程度与逆变器台数n、电网等效阻抗Lg有关。

由式(12)—(13)推得多机并联系统的耦合将额外引入一谐振频率为fadd的谐振点，其表达式为：

(16)

故当LCL滤波器参数确定后，谐振频率fadd仅与逆变器台数n、电网等效电感Lg有关。为分析弱电网下fadd随n的变化规律，图4给出了二者的函数关系，相关参数取值见表1，谐振频率fadd随逆变器台数n的增加而逐渐变小。

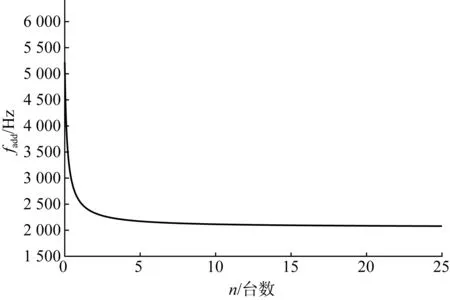
图4 谐振频率fadd与逆变器台数的函数关系Fig.4 Functional relationship between resonance frequency fadd and the number of the inverters

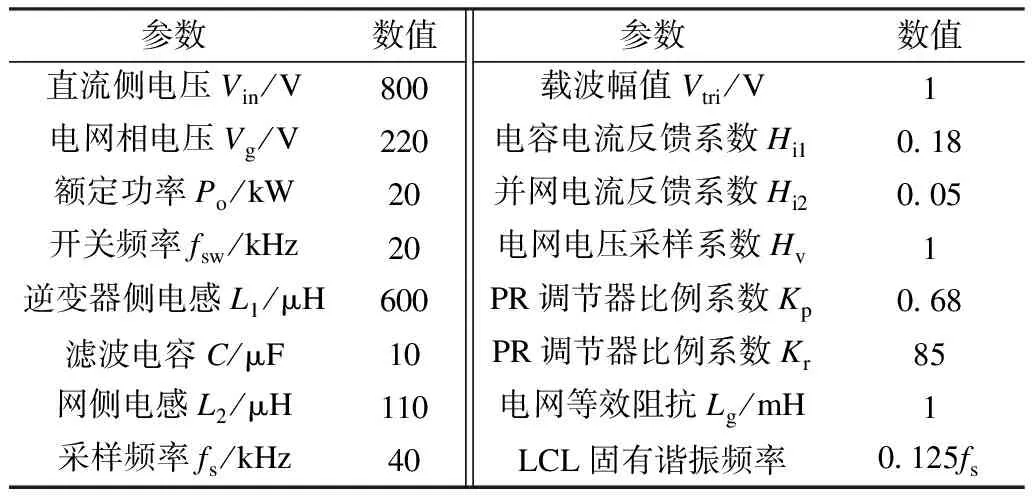
表1 逆变器相关参数Tab.1 Relevant parameters of the inverter

2.2 多机并联系统稳定性分析

为分析多机并联系统的稳定性，结合诺顿定理分析式(5)可将单台逆变器等效为电流源并联自身闭环输出导纳的模型[23]，模型中电流源增益由式(5)可得：

(17)

逆变器闭环输出导纳为：

(18)

图5为基于上述推导得出的多机并联系统的闭环诺顿等效电路。为简化分析，该系统中各逆变器选取同样的参数与控制算法，故有：

(19)

式中：Gcsi(s)为第i台逆变器的电流源增益；Yoi(s)为第i台逆变器的闭环输出导纳。

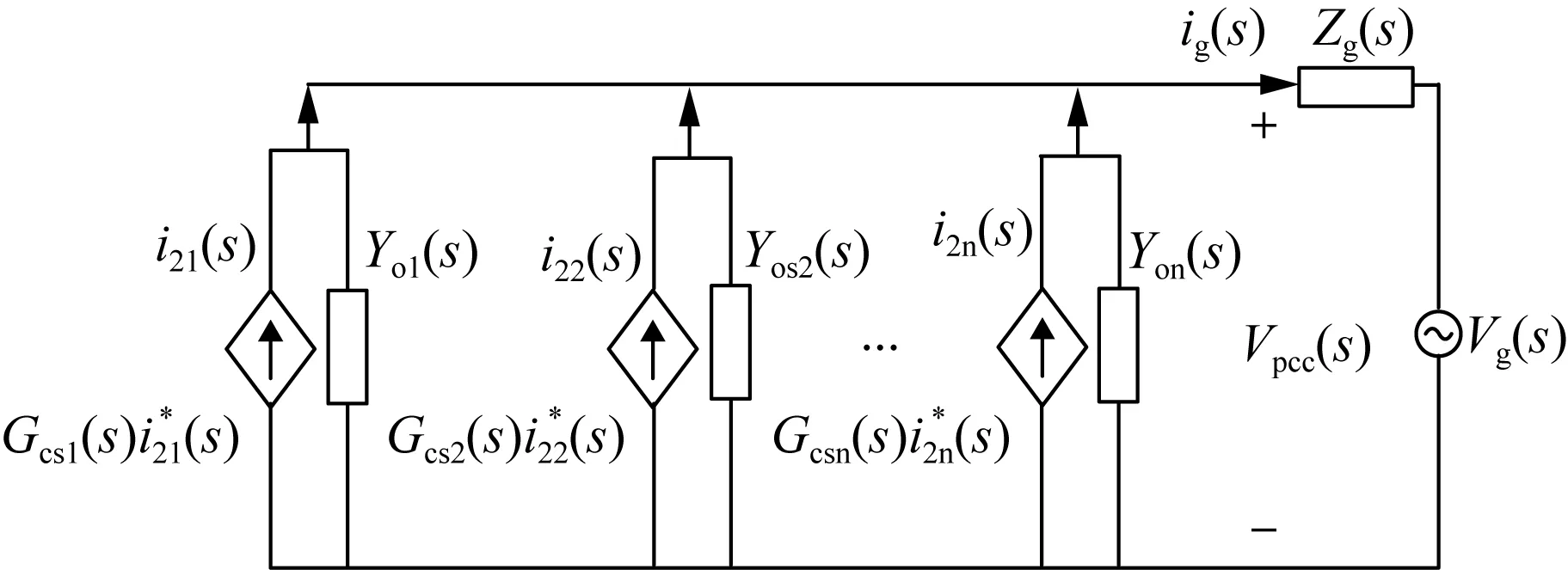
图5 多机并联系统闭环诺顿等效电路Fig.5 Closed-loop Norton equivalent circuit of multi-machine parallel system

通过叠加定理分析图5可得闭环多机并联系统中第i台逆变器输出并网电流为：

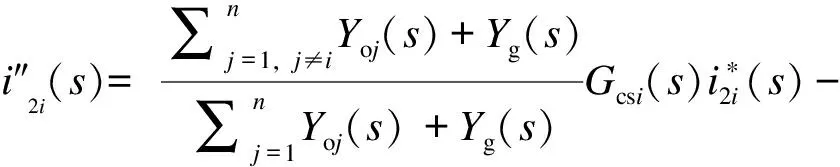
(20)

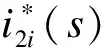
(21)

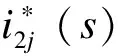
此时，多逆变器并联系统的总输出并网电流为：

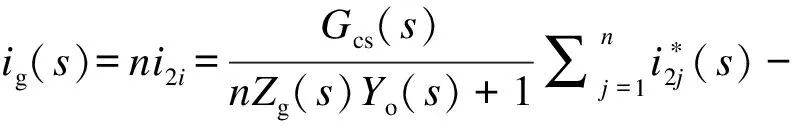
(22)

本节重点关注多机并联系统的整体稳定性，故默认系统中各逆变器单独工作时可稳定运行，即各逆变器闭环诺顿等效模型中电流增益Gcs(s)与导纳Yo(s)无右半平面极点，分析式(21)和(22)可得：

(23)

无右半平面极点时多机并联系统保持稳定。要想解析G*(s)的极点位置需要首先求得G*(s)的环路增益nZg(s)Yo(s)的极点位置，但由于Zg(s)和Yo(s)项均无右半平面极点，故仅当nZg(s)Yo(s)的Nyquist曲线包围(-1,j0)的圈数为0时，G*(s)无右半平面的极点[24]。为便于分析多机系统稳定性，这里定义：

(24)

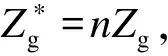
为提高本文研究的适用性，多机并联系统中的逆变器均选用电容电流比例反馈和电网电压比例前馈控制，并且选用Lg=1 mH模拟弱电网环境。图6表示n取不同值时环路增益T*(s)的Nyquist曲线。

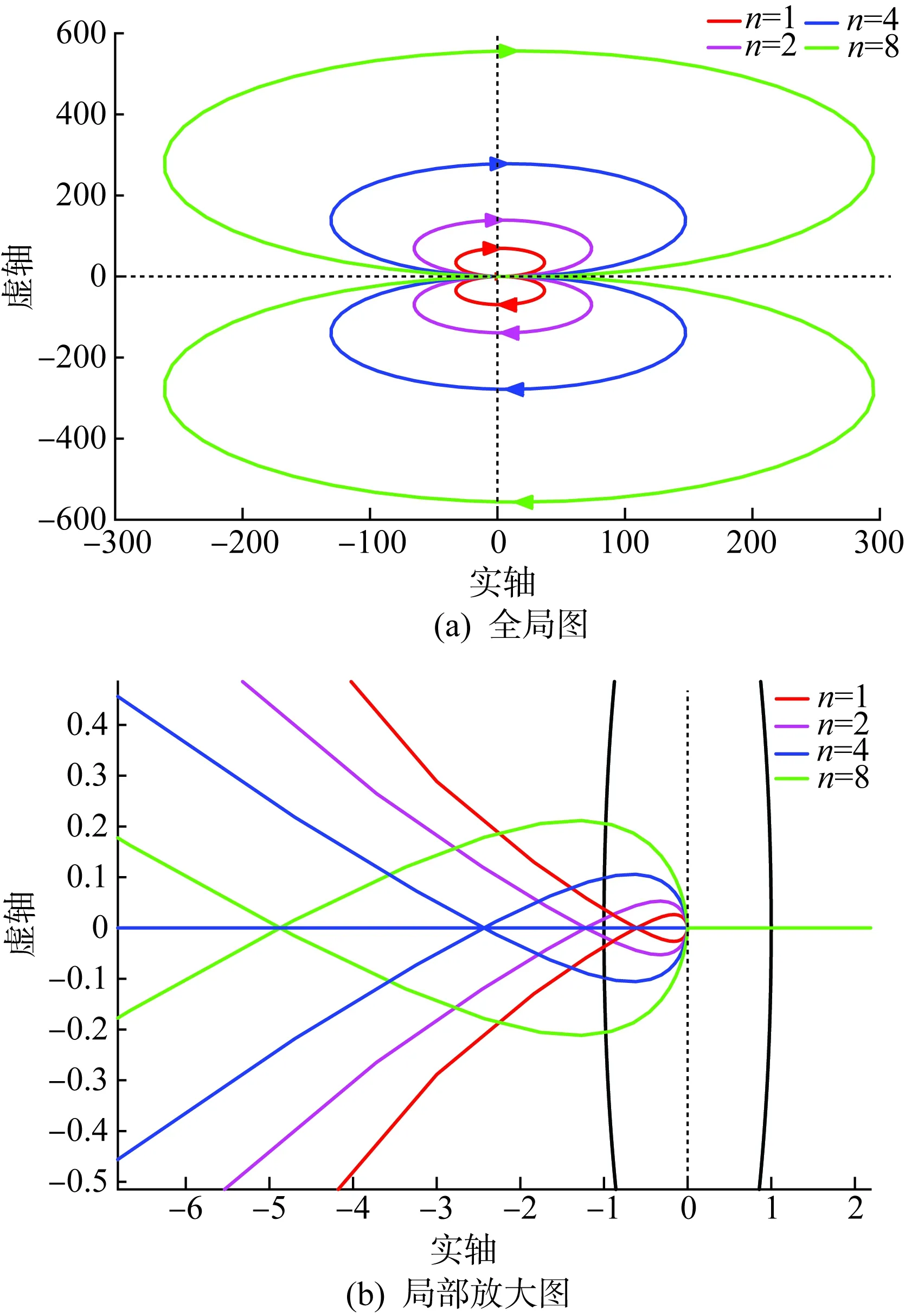
图6 环路增益T*(s)的Nyquist曲线Fig.6 Nyquist curves of the loop gain T*(s)

观察图6可知：当n=1时，T*(s)的Nyquist曲线包围(-1,j0)点的圈数为0，但此时Nyquist曲线距离(-1,j0)点较近，即此时系统的稳定裕度较小。随着n逐渐变大，T*(s)的Nyquist曲线范围也不断扩大，当n≥2时，T*(s)的Nyquist曲线开始包围(-1, j0)点，表明多逆变器并联系统失去原有单机稳定性。随着多机并联系统中n的增大，系统的稳定性逐渐降低，最终导致系统发生谐振。

3 PCC点并联虚拟导纳的整机谐振抑制法

基于上一节的分析可知，假定在PCC点处并联一虚拟导纳Yk(s)，其在遇到总并网电流ig(s)的基波分量时呈现高阻态，而在遇到谐波电流时呈现低阻态，此时通过虚拟导纳Yk(s)可吸收并网电流ig(s)中的谐波电流，进而有效提高了多逆变器并联系统输出电流质量，图7为上述方法的等效电路。

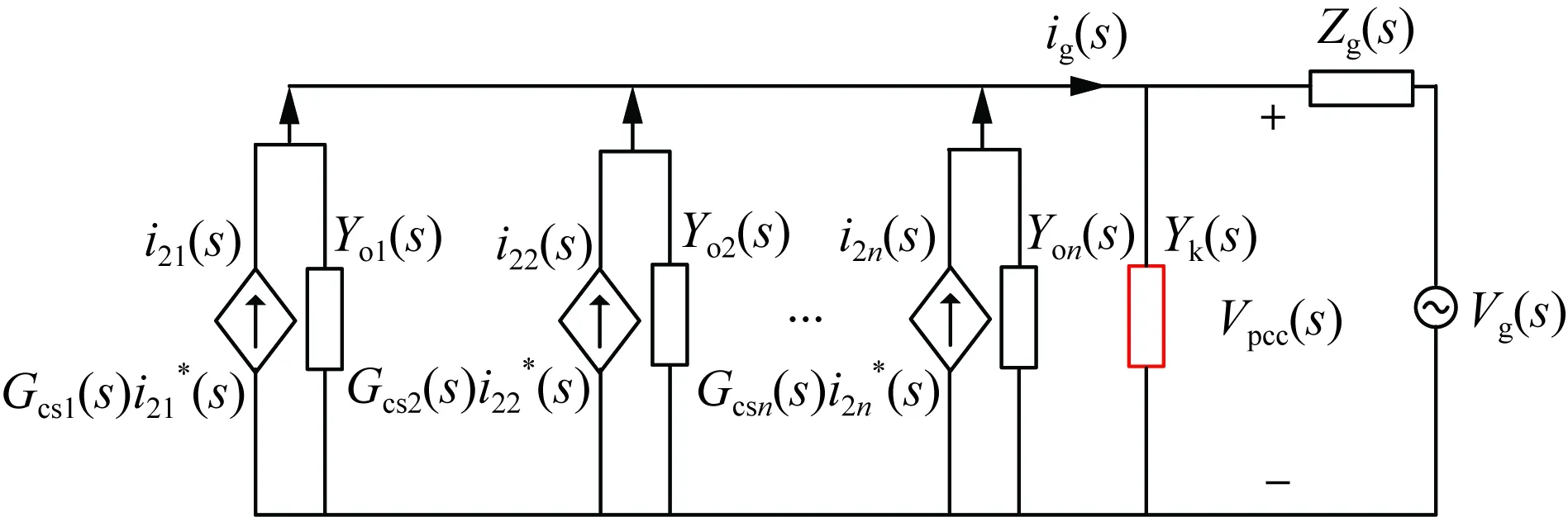
图7 PCC点加入虚拟导纳后的等效电路Fig.7 Equivalent circuit after adding the virtual admittance in the PCC point

基于二阶广义积分器的陷波器可大幅衰减特定频率处的输入，而在其余频段内可维持输入[25]，这一特点满足本文所需并联虚拟导纳Yk(s)的要求，其传递函数为：

(25)

式中：m为陷波器频率系数；ω0为陷波器基波角频率。

图8为m取不同值时GTrap(s)的伯德图。

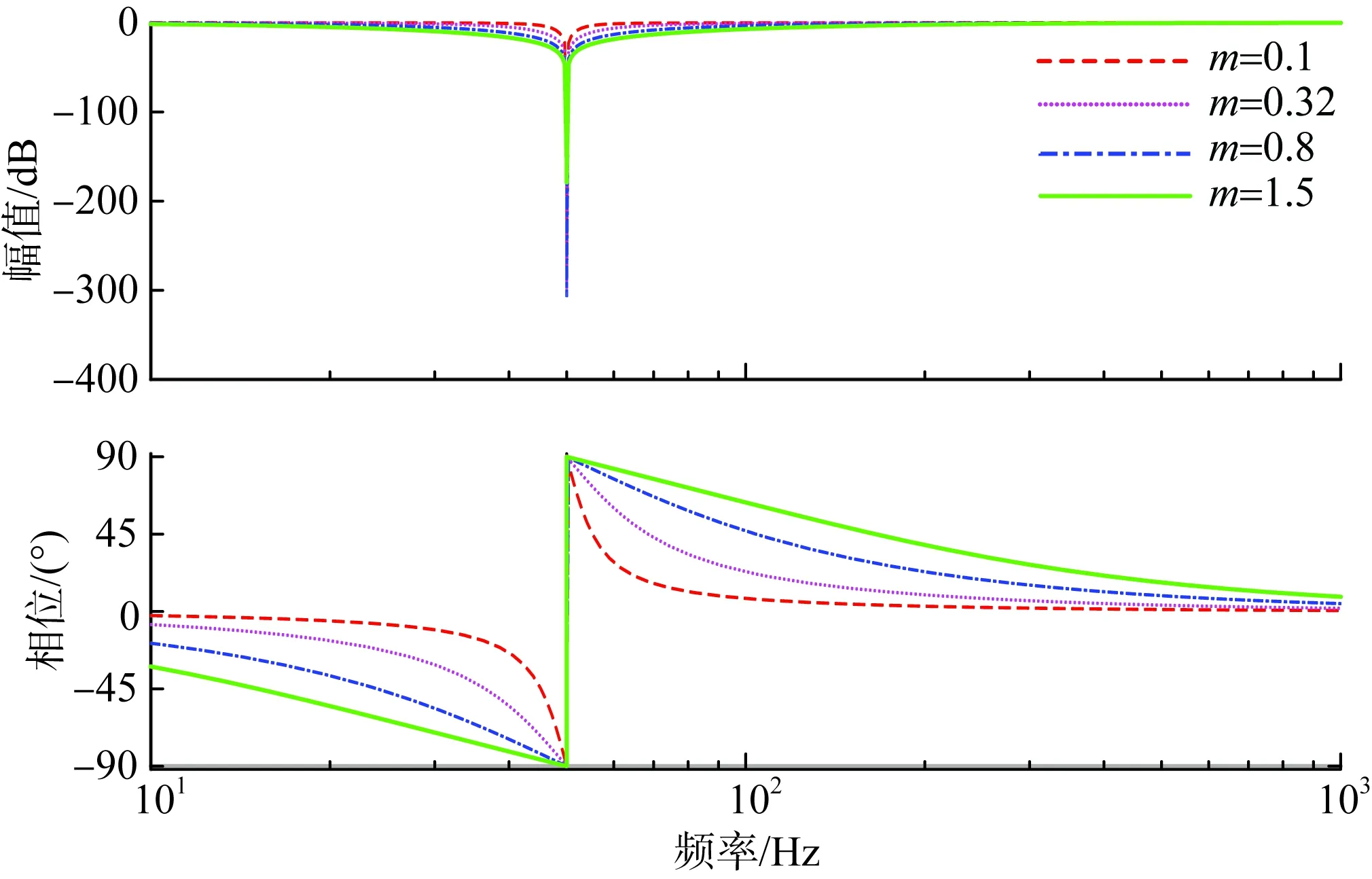
图8 不同m下陷波器的伯德图Fig.8 Bode diagram of notch filter with different m

观察图8可知：在基频处的信号会被大幅衰减，而其余频段信号可无衰减地通过陷波器。此外，陷波器频率系数m的取值会影响GTrap(s)的伯德图，若m值较小，则GTrap(s)在基频处的尖峰区域较小，表明其分离基频和非基频输入信号的能力较强；反之，若m值较大，则GTrap(s)在基频处的尖峰区域较大，表明其分离基频和非基频输入信号的能力较弱。因此，在设计陷波器频率系数m时，需兼顾其电网频率波动适应能力与非基频信号分离能力，折中选定m。理想情况下逆变器输出电流为光滑正弦信号，为此当陷波器GTrap(s)有一正弦输入y(t)=Asin(ω0t)时，其输出为：

(26)

从式(26)可知，根号下的因式(1-0.25m2)应大于0，解得频率系数m<2。此外，系统的调节时间为：

ts=10/(mω0)

(27)

观察式(27)可知，随着m的取值变大，系统的调节时间逐渐减小，即系统趋于稳定的速度越快。为使系统获得较优的动态响应，增强完整保留非基频信号的能力，选用最优二次系统的设计方法[26]，本文选取频率系数m=0.32。

为便于分析，进一步将图7中的并联虚拟导纳Yk(s)等效前移至每台逆变器侧，记为Yki(s)，图9为前移等效后的电路。

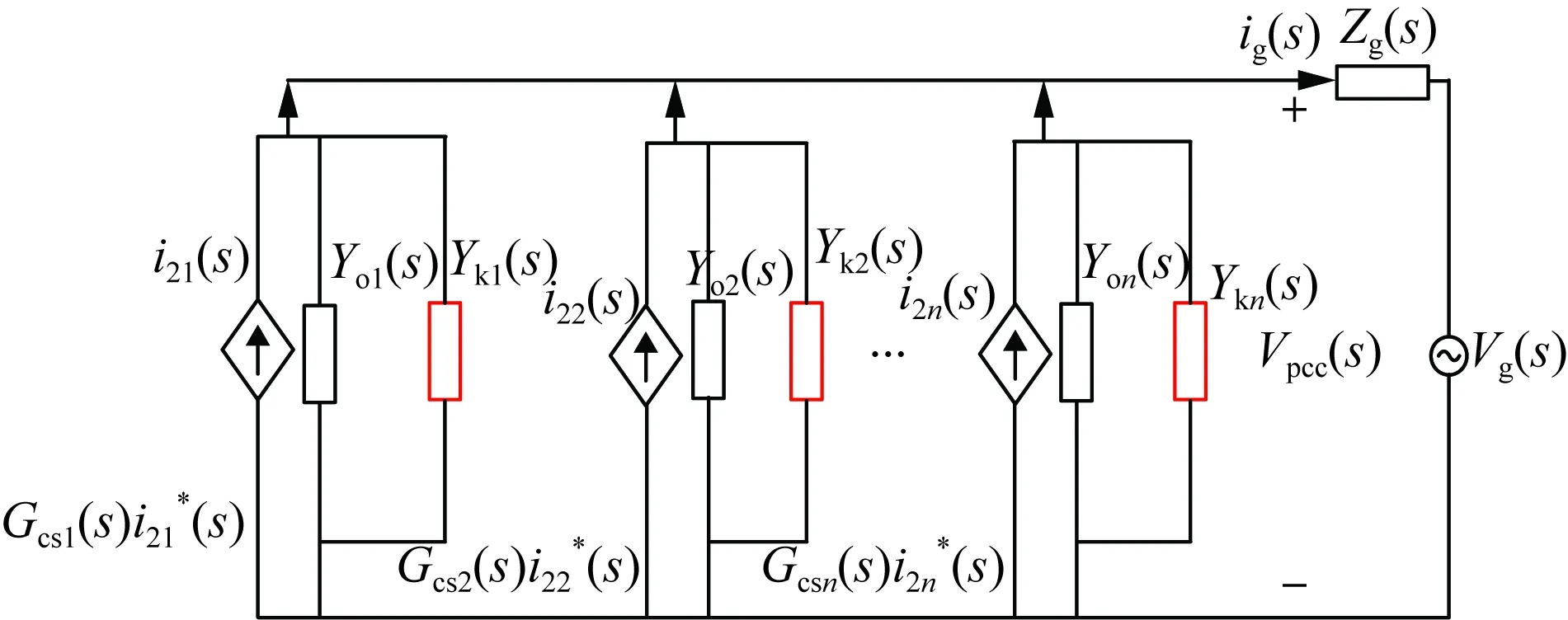
图9 图7的等效电路Fig.9 Equivalent circuit of the figure 7

为实现图9中Yki(s)的控制效果，可采集PCC点总并网电流或流经各逆变器的并网电流，如果选择前者，则仅需在多机并联系统中任一逆变器侧添加虚拟导纳，便可实现滤除总并网电流ig(s)中的谐波电流；同样，也可选择将虚拟导纳前移至每台逆变器的控制策略。为便于进行理论分析，本文选用在每台并联逆变器中并入虚拟导纳的策略，图10为所提增加虚拟导纳策略的控制框图，通过虚线内环节实现添加虚拟导纳。

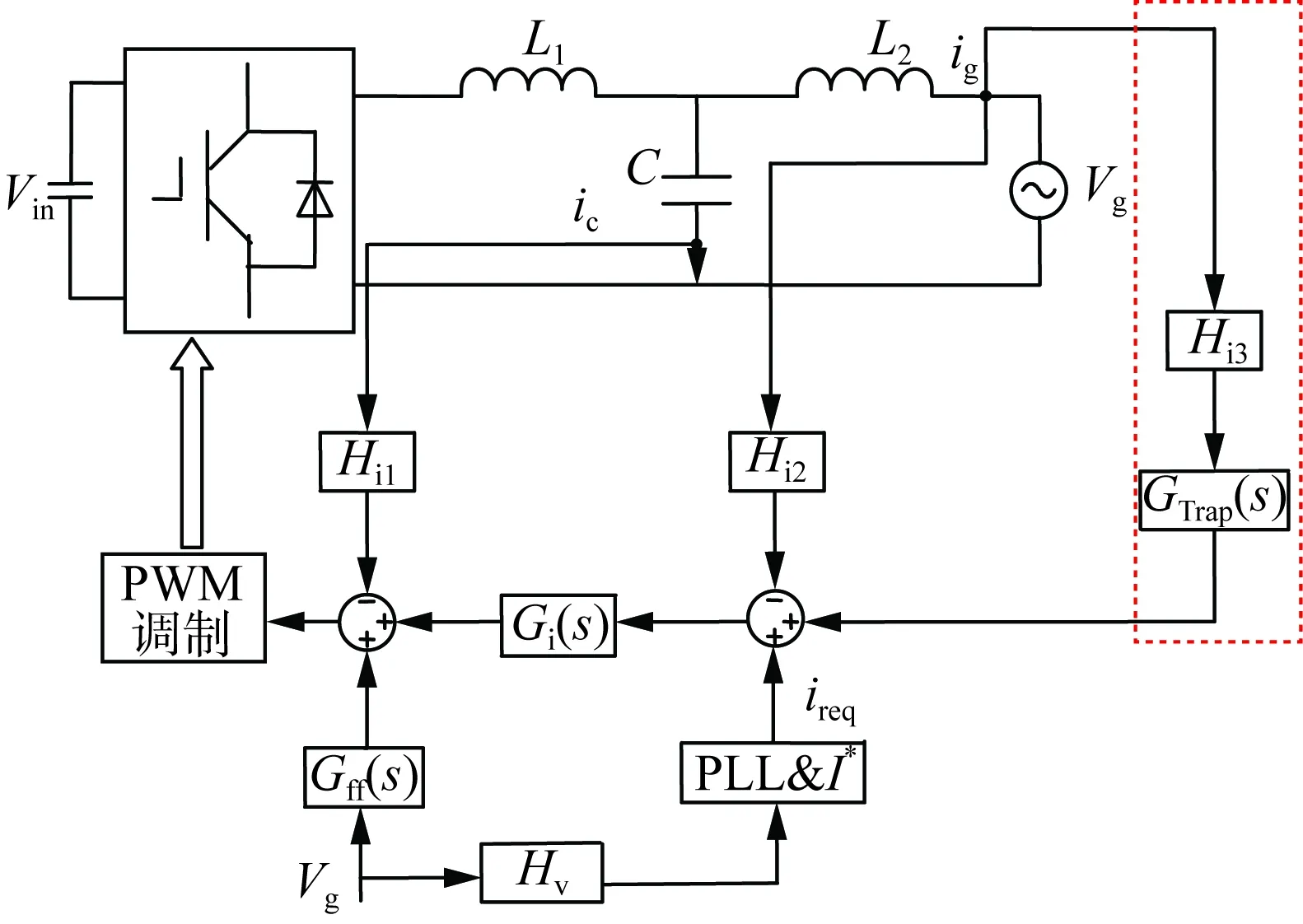
图10 含虚拟导纳的逆变器原理图Fig.10 Schematic diagram of the inverter including virtual admittance

参考图2逆变器输出阻抗推导过程，对比图2(a)与图10可知，引入虚拟导纳相当于增加了一条并联反馈支路-Hi3GTrap(s)，参考图2(c)的化简过程，可将所提控制策略在α轴上的控制框图等效为图11。

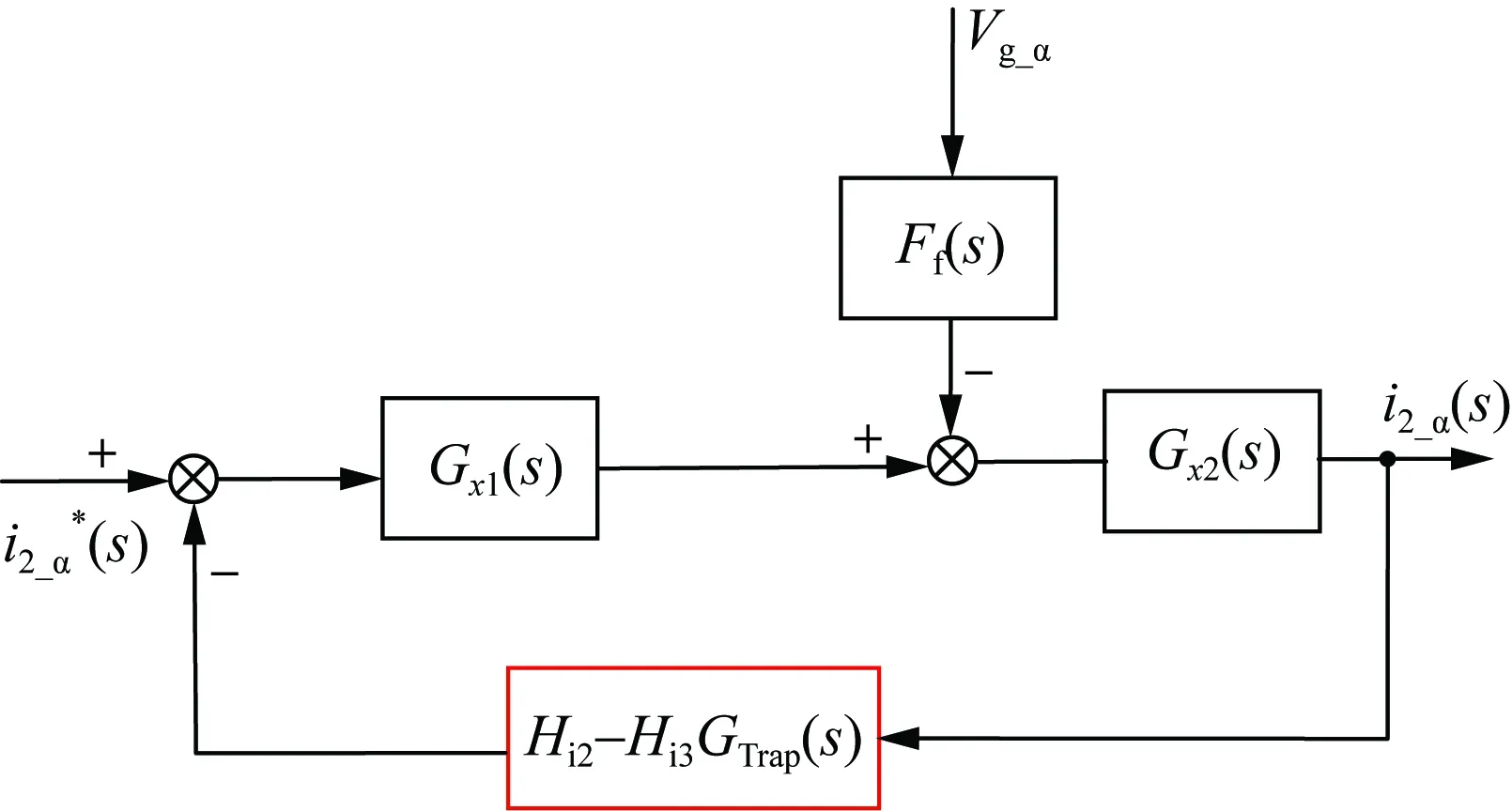
图11 α轴上图10的等效控制框图Fig.11 Equivalent control block diagram of figure 10 on the α-axis

分析图11与式(7)，可得出增加虚拟导纳后逆变器闭环输出阻抗表达式为：

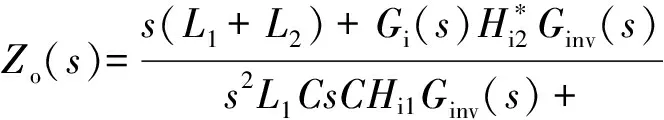
(28)

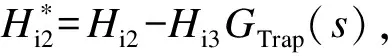
为解析虚拟导纳系数Hi3与逆变器输出阻抗的关系，图12给出了Hi3取不同值时逆变器输出阻抗的伯德图。

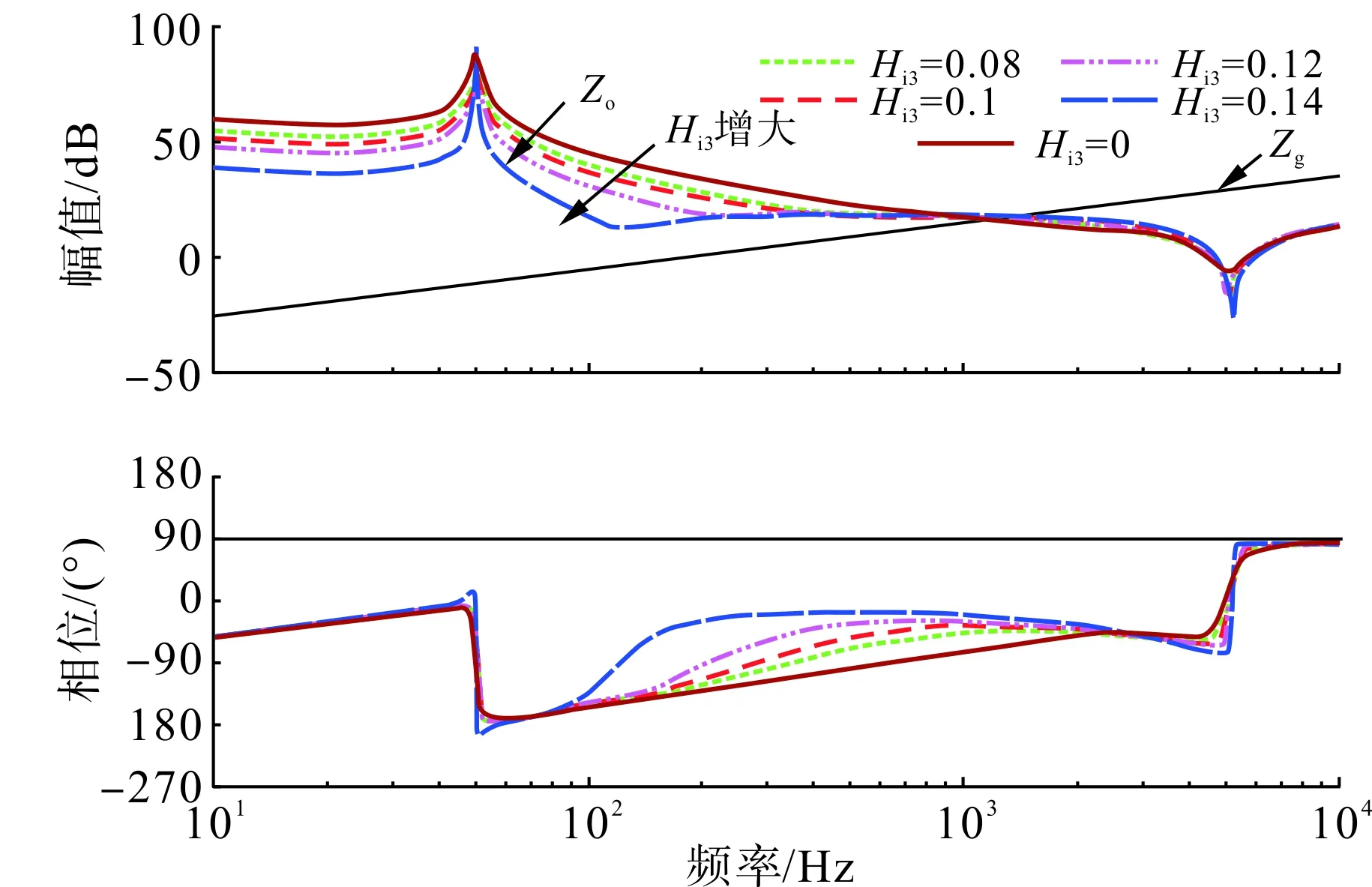
图12 不同Hi3下的逆变器输出阻抗伯德图Fig.12 Output impedance Bode diagram of inverter with different Hi3

观察可知，Hi3取值越大，逆变器输出阻抗的相角裕度越大，即在电网等效阻抗Zg与逆变器输出阻抗Zo的幅频特性曲线交点处的输出阻抗相位与-90 °的距离越远[27 - 28]，且系统在基频处的增益和未加入虚拟导纳时的输出阻抗(即Hi3=0)大小相等，导致逆变器控制单元的稳态误差限制得较低，但低频处的幅频特性曲线随Hi3的增大逐渐向下移动，故选取虚拟导纳系数Hi3=0.12，其余参数见表1。

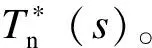
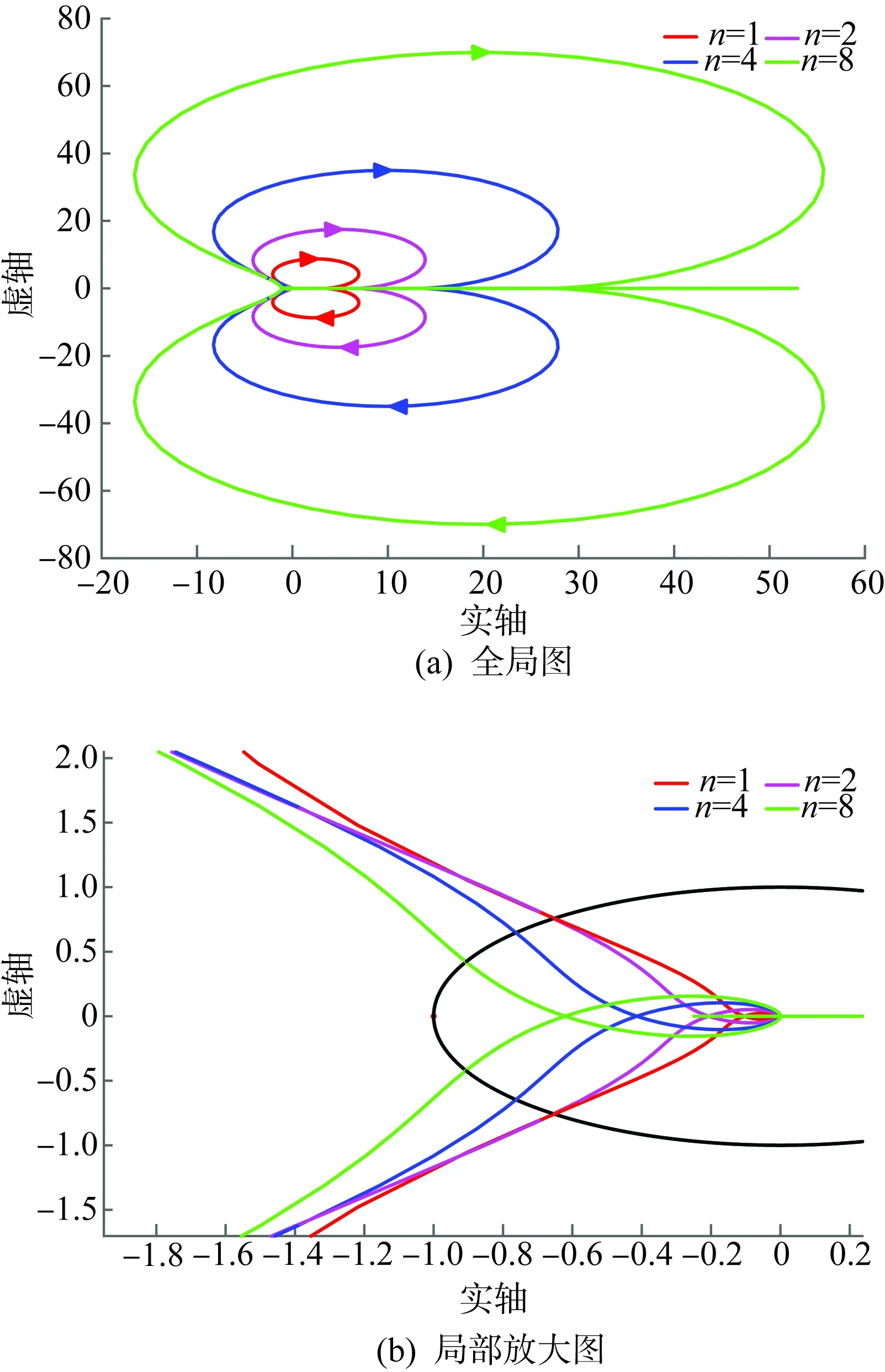
图13 环路增益的Nyquist曲线Fig.13 Nyquist curves of the loop gain

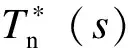
4 仿真与实验验证

4.1 仿真分析

为验证本文所提策略的有效性，在Simulink软件中搭建多并网逆变器并联系统的仿真模型，逆变器相关参数见表1。

图14为Lg=1 mH，n=2、4时多机并联系统的总输出电流波形与频谱图。由于弱电网下Lg≠0，各逆变器间彼此耦合，并网电流谐波畸变率较高且随着n的增加而升高，多机系统的稳定性逐步下降，系统发生谐振，符合第2节稳定性分析相关结论。此外，由图14可知，多机并联系统的谐振频率随逆变器台数的增加而减小，与式(16)分析结果一致。

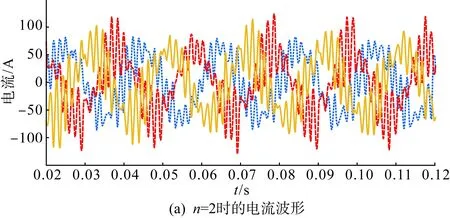
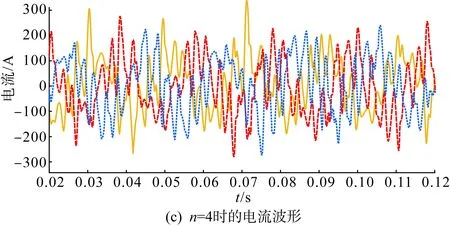
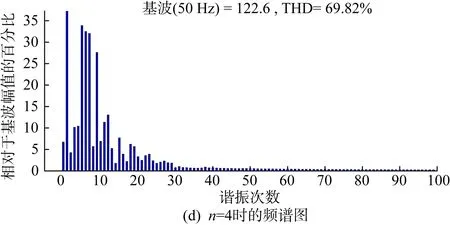
图14 Lg=1 mH，多机并联系统总输出电流波形及频谱图Fig.14 Lg=1 mH, total output current waveforms and spectrum map of the multi-machine parallel system

图15为Lg=1 mH，n=2、4时增加虚拟导纳后多机并联系统总输出电流波形与频谱图，对比图14可知，采用本文所提控制策略后，并网电流谐波畸变率大幅下降，电流质量明显提高，谐振得到有效抑制，仿真结果与图13中的理论分析结果一致。

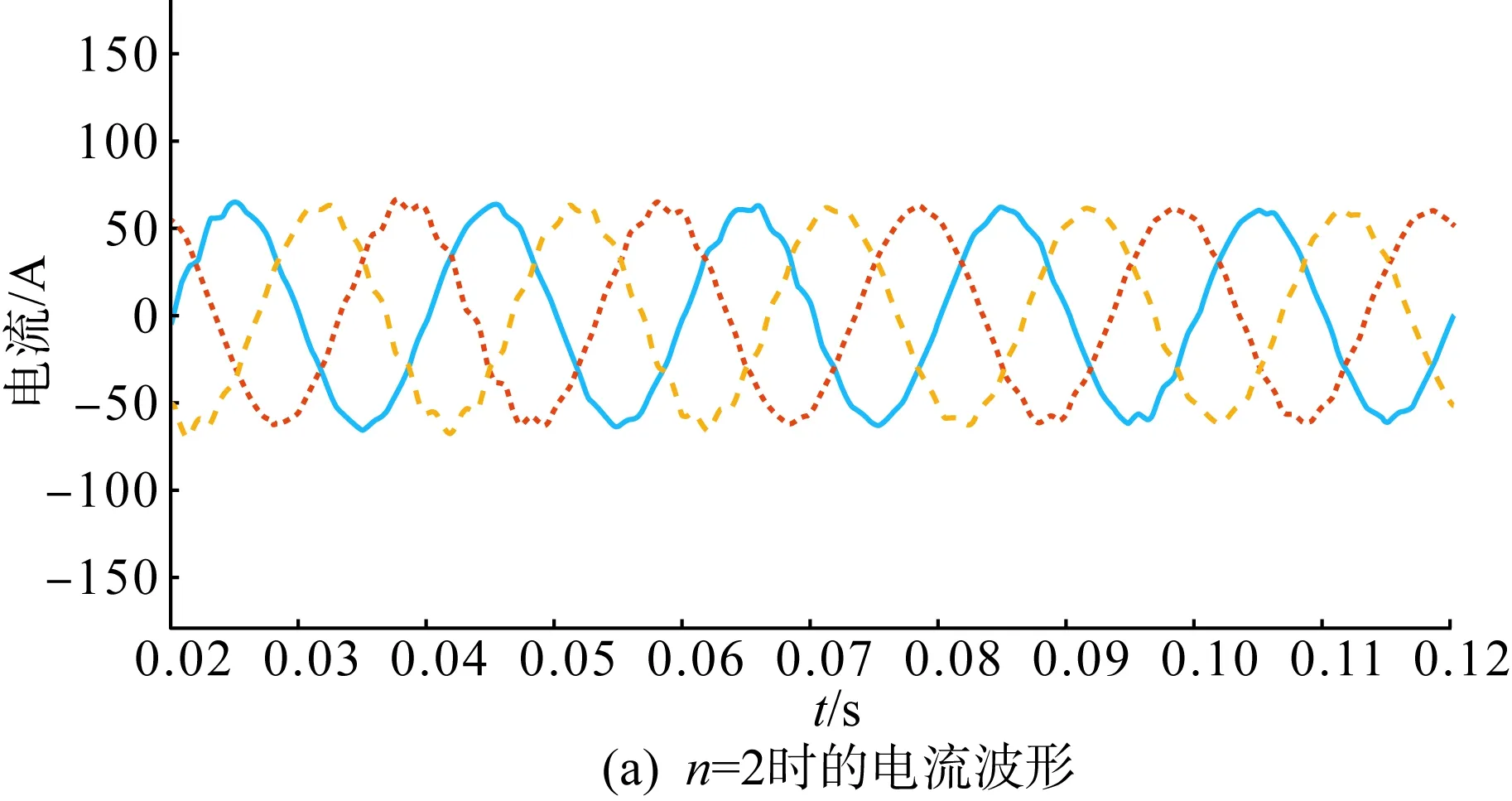
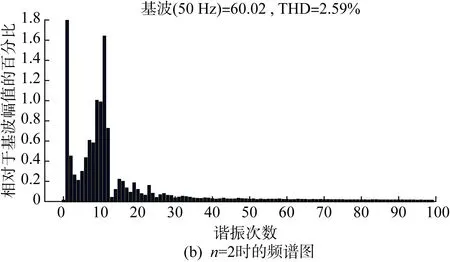
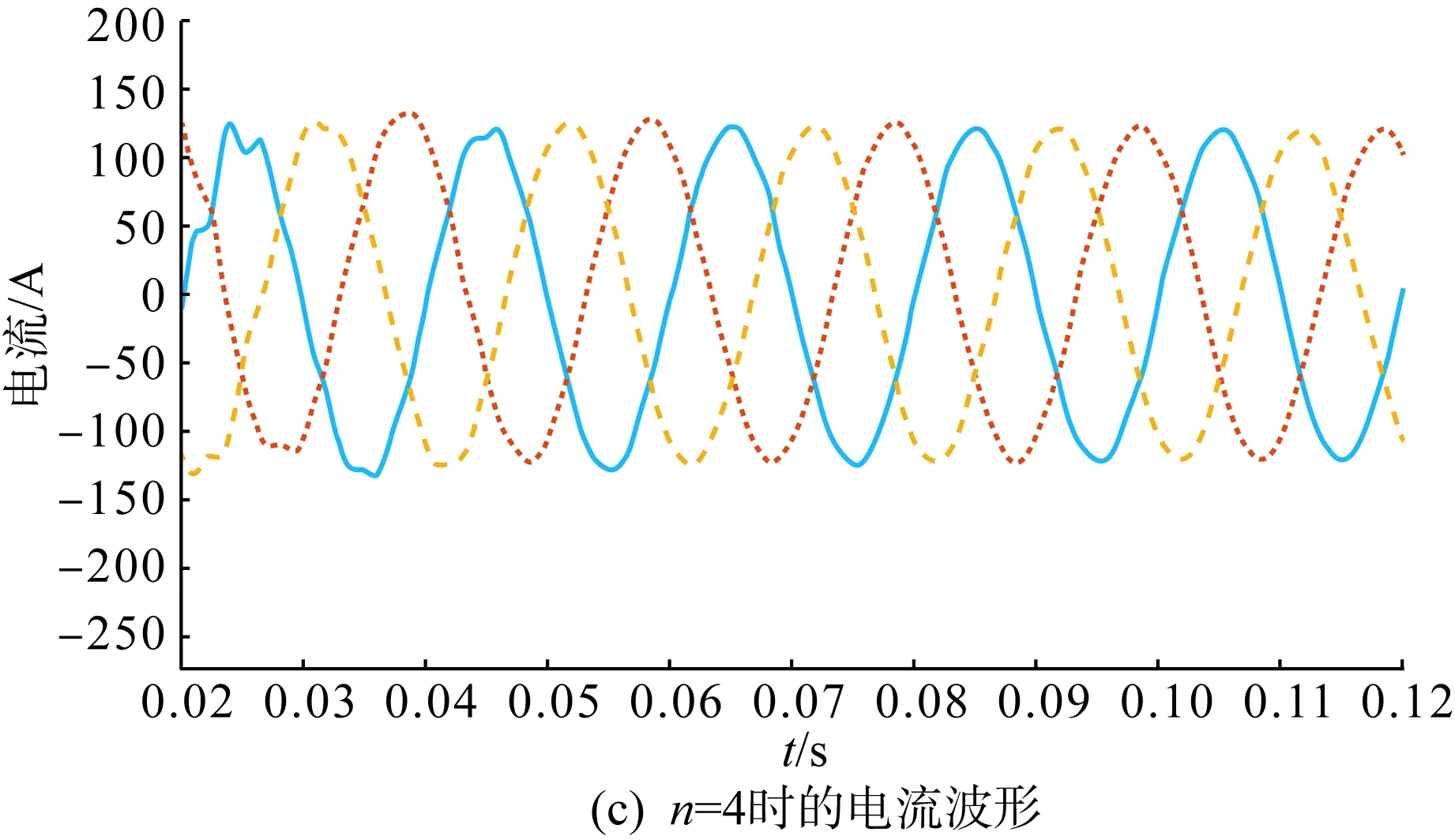
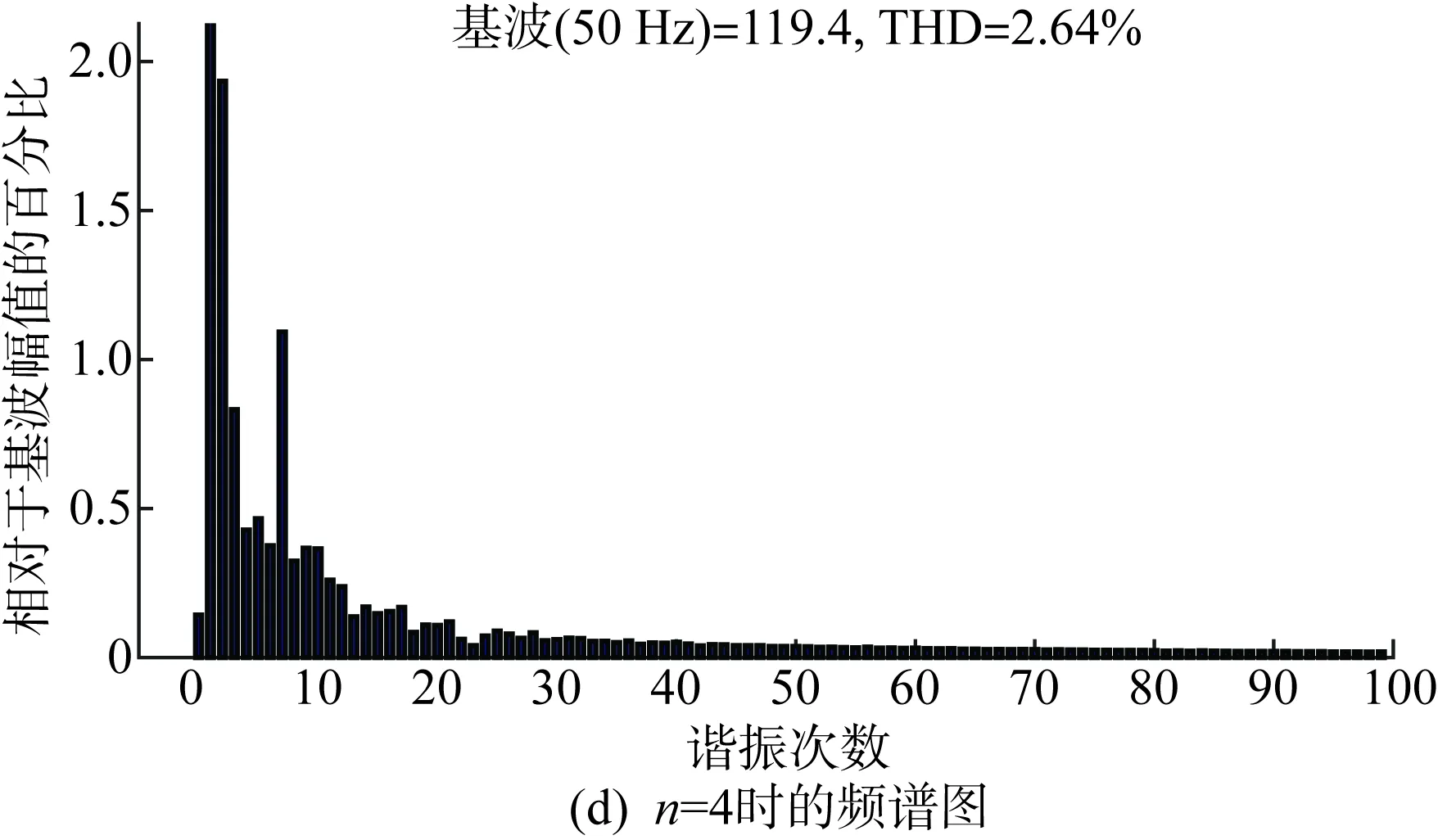
图15 Lg=1 mH，增加虚拟导纳后多机并联系统总输出电流波形及频谱图Fig.15 Lg=1 mH, total output current waveforms and spectrum map of the multi-machine parallel system after adding virtual admittance

4.2 实验验证

为进一步验证本文所提多并网逆变器并联运行的谐振抑制策略的控制效果，搭建两台逆变器并联运行的实验平台如图16所示，实验参数与表1保持一致。为模拟弱电网环境，在PCC点处串入0.5 mH的电感。

图16 弱电网下2台逆变器并联实验平台Fig.16 Experiment platform of two parallel-inverters under weak grid

图17分别为弱电网下未增加虚拟导纳与增加虚拟导纳时两台逆变器并联时总并网电流波形。图17(a)中，由于弱电网下电网等效阻抗的存在，逆变器间及逆变器与电网间彼此耦合，造成总并网电流畸变严重；图17(b)中,当在多机系统中增加虚拟导纳时，由于虚拟导纳吸收了并网电流中的谐波分量，使得总并网电流质量较高，保证了弱电网下多机并联系统的稳定性，系统谐振得到抑制，这与图13中的理论分析结果以及上述仿真结果一致。分析实验结果可知，本文所提控制策略能够在弱电网环境下有效抑制多逆变器并联系统中的谐振现象。

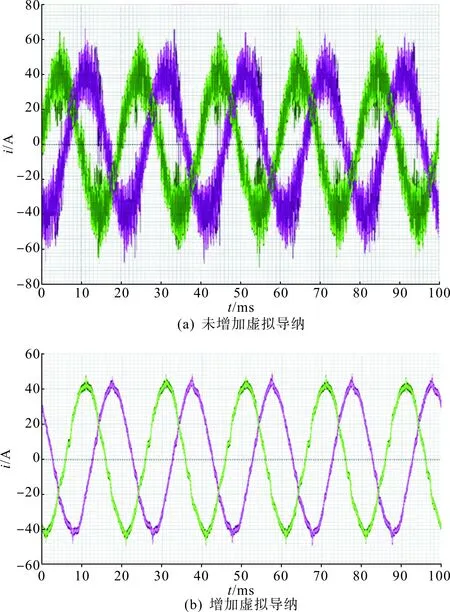
图17 n=2时,增加虚拟导纳前后总输出电流波形Fig.17 n=2, total output current waveform before and after adding virtual admittance

5 结论

本文分析了多机并联系统的谐振特性，构建了弱电网环境下多机并联系统的闭环诺顿等效模型，基于该模型推导出判别多台逆变器并联运行稳定性的Nyquist判据，解析了采用传统电网电压比例前馈控制方法时多机并联系统存在稳定性低、整机谐振等问题的原因。并提出了基于陷波器向PCC点加入虚拟等效导纳的整机谐振抑制策略，该策略有效提高了多机并联系统的稳定裕度，使系统满足多台逆变器并联运行的Nyquist稳定判据，通过仿真和实验进一步论证了所提策略可有效抑制弱电网环境下多逆变器并联系统的谐振现象。