基于阵列盖革探测器的激光测距信号处理

王皓民,白一波,耿 林,韩 隆

(华北光电技术研究所,北京 100015)

1 引 言

距离测量技术在工程建设、科学研究、计量、测绘以及军事领域有着极其重要的作用,在各种距离测量技术中,性能最高、发展前景最好的是激光测距技术。激光距离测量系统因体积质量小、精度高,以及响应速度快等优点被广泛应用于远距离测量、大气浓度监测、激光三维成像、星地激光测距[1]等各个领域。

激光脉冲测距应用于远程测距中,回波信号的回波率与距离R的平方(大目标)或R的四次方(小目标)成反比。在某些特定情况下,激光回波能量会小到光子量级,要有效获得回波信号,就需要光子量级的探测能力和信号处理能力。

单光子探测器(Single Photon Avalanche Diodes,SPAD)是一种有效的单光子量级探测器件[2],是近年来研究、应用的主要器件类型之一。具有单光子探测能力的器件有光电倍增管、超导纳米线单光子探测器、超导雪崩二极管(SAPD)、多像素光子计数器(MPPC)[3]等。

单光子激光测距国外发展较早,美国已进行了数十年的研究。20世纪90年代,美国麻省理工学院(MIT)林肯实验室首先研制出了阵列APD探测器件,并于本世纪初应用于盖格模式APD阵列的激光三维雷达,其中代表作有Gen系列激光雷达系统[4-5]。美国APOLLO站也将阵列用于地月距离测量并取得显著成果[6-8]。

2017年,西南交通大学课题组和美国NIST团队合作,实现了能量分辨率为220 meV,在1550 nm波段可分辨7个光子的微波动态电感单光子探测器(MKID)[9]。南京大学于2008年研制出我国首个超导纳米线单光子探测器(SNSPD),目前已研制出的系列SNSPD器件在1550 nm波段探测效率超过90 %[10]。中国云南天文台于2015年开展了基于阵列探测技术的激光测距试验,2017年成功将阵列超导纳米线单光子探测器和多通道事件计时器等阵列探测技术应用于激光测距试验系统中,分别于2017年3月和2018年3月,成功采集阵列激光测距数据[11]。2021年3月,中科大潘建伟院士团队使用单光子成像雷达实现了201.5 km单光子三维成像,成像灵敏度达到平均每个像素0.4个信号光子。

使用单光子探测器主要面临的问题是测距信号经过大气的衰减和背景噪声等影响,漫反射回波光子数量极少,少数回波光子被淹没于大量噪声中。同时由于探测器灵敏度等问题,到达探测器端的光子仍旧有概率不被探测到。因此目标光子的接收提取十分困难,需要对接收到的负信噪比信号进行处理。

本文主要讨论基于阵列盖革单光子探测器的测距体制信号处理方法,并进行了基于光子计数法的信号仿真。本文主要研究的信号处理方法有以下三种:(1)多通道累加算法;(2)空间卷积池化算法;(3)阵列拓展算法。

2 系统特性

盖革模式APD的特点是能够响应光子的有无,不能响应光子的强弱,即同一时刻单个光子在探测单元被响应时会产生一个‘1’信号,多个光子在探测单元响应也只会产生一个‘1’信号。因此,这种模式下不关注信号强度,仅关注于是否能够接收到信号,但信号的长度能够影响信号相对于背景噪声的辨识程度。

远程激光测距通过飞行时间法中信号回波的过程,我们可以近似看成极远处有数十个光子向探测器射来,类似于图1所示的一种“投球实验”。距离较近时,会在二维空间中呈现类高斯分布,即越靠近中心光子分布的概率越大；随着距离变远,这种分布特点在探测器端会逐渐模糊,趋于平均分布[12]。同时,由于空间光传输信道中存在各种干扰,接收端信号光子的分布更加复杂,因此在后续的讨论和仿真中会根据不同情况选择更合理的光子分布模型。

图1 光子“投球实验”示意图Fig.1 Illustration of photon ‘throwing experiment’

本文仿真中接收端信号光具备类高斯分布,背景光服从均匀分布,噪声为平均每100个信号会响应95个的背景噪声光子。接收端采用4×4的探测器阵列,成方形分布,间距较小。光束空间传输散布如图2所示,其中深色点表示信号光,浅色点表示背景光。信号光、背景光分别如图3、图4所示。

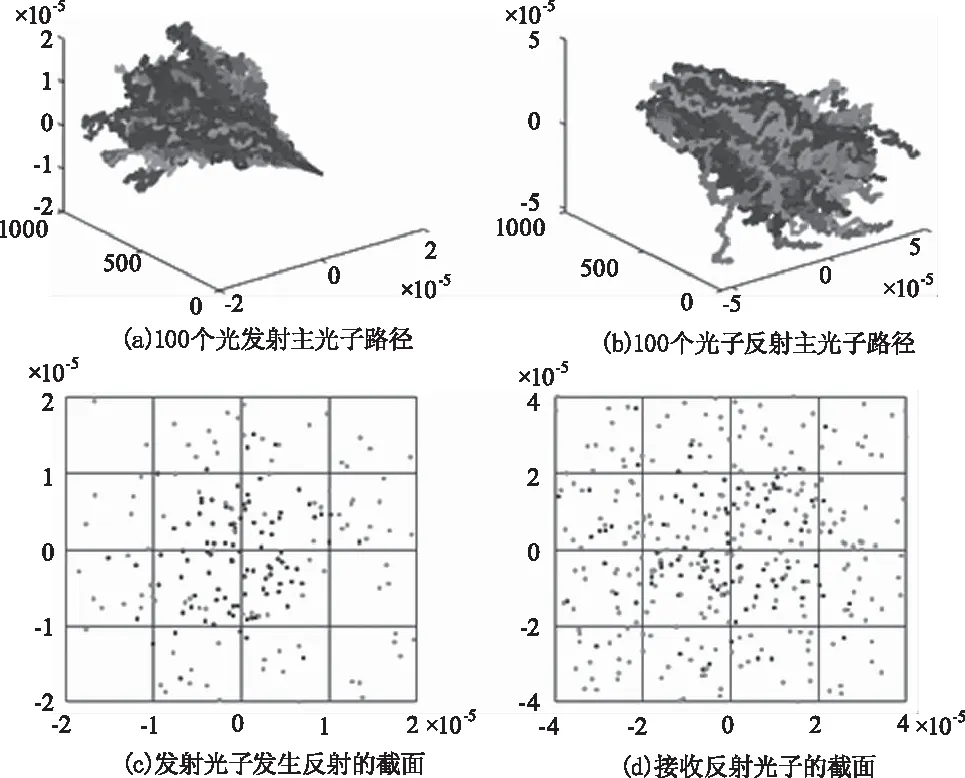
图2 信号光分布示意图Fig.2 Illustration of signal light distribution

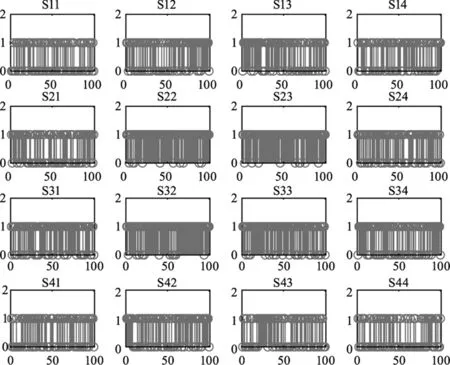
图3 信号光分布示意图Fig.3 Illustration of signal light distribution

图4 噪声分布示意图Fig.4 Illustration of noise distribution

将长度为100的仿真信号光信号插入长度为10000的仿真背景光信号中构成了长度为10000的仿真接收信号。对仿真接收信号进行光子计数法操作,即一维线性卷积操作,信号如图5所示。

图5 仿真模拟接收信号示意图Fig.5 Illustration of receiving signal

本文后续算法均采用图5中产生的仿真模拟接收信号进行操作,目的在于恢复信号光经目标反射返回被探测到的时刻。

3 盖格模式阵列信号处理

3.1 多通道累加算法

由于接收信号的信噪比低,需要对原信号进行恢复,此处作为基础方法选择最简单的多通道累加算法,以提高信噪比。

由于多个探测器分布较近,可以忽略由于位置不同带来的信号影响,即假设不同探测器每次接收到的反射信号几乎相同。同时,发送端将测距信号等间隔发送,以此在不同探测器和不同时间点获得多个可用于累加的信号。

接收端接收到的信号为:

allES16=ES11+ES12+ES13+ES14+ES21+

ES22+ES23+ES24+ES31+ES32+ES33+ES34+ES41+

ES42+ES43+ES44

(1)

其中,allES为全部的接收信号;ESij为第i行第j列个通道所接收到的信号。

每个通道接收到的信号可以表示为:

ESij=f(t)+nij(t)

(2)

累加后:

allES16=16f(t)+∑nij(t)

(3)

多次接收的噪声信号同分布且相互独立,对其进行多次累加后依旧服从高斯分布。但由于信号累加时为幅度叠加,噪声累加时为功率叠加,因此多次累加取平均后的信号的信噪比会得到很大改善。

如果噪声为零均值的高斯分布,多次累加后依旧为零均值,因此对接收信号进行预处理,使噪声为零均值,可以获得更好的效果。累加后的信号如图6所示。

图6 多通道累加算法仿真图Fig.6 Results of multi-channel accumulation algorithm

通过图5与图6中信号的对比可以发现,通过信号累加后产生了一个明显的尖峰,尖峰顶点即为多通道累加算法解算出的信号光响应时刻。

此处仅进行了16个通道的累加,如果运用时间维度,等间隔发送信号并分开累加后效果更好。同时,如果采用最大比合并,理论上效果会更好,但在实际应用汇中,长距探测时背景噪声可看作服从均匀分布,不同探测器在同一时间范围内收到的信号信噪比类似,因此采用最大比合并意义不大。

3.2 空间卷积池化算法

空间卷积池化算法,是结合光子计数法和阵列,进行二维离散卷积后池化,对具有时间长度、空间散布的空间信号进行辨识的方法,其步骤如图7所示。

图7 空间卷积池化算法Fig.7 Illustration of the spatial convolutional pooling algorithm

第一步,将接收信号进行光子计数法处理得到如图4所示的阵列模拟信号；第二步,采用不同卷积核进行逐帧卷积处理,随后池化得到一维信号解算出信号光入射时刻；第三步,由于卷积核和池化层具有多样性,不同卷积核卷积和池化方法会得到不同的解算信号,将多组信号比照后,可以获得更多的信息。

如果直接对16个通道的信号进行最大池化,即:

allES=max(max(ES16))

(4)

结果如图8所示,还不能看出信号的入射时刻。

图8 直接对图4信号进行池化的效果仿真图Fig.8 Simulation results of pooling the signals in Fig.4

随后采用卷积核先对原始阵列信号进行卷积,再进行池化,累加,即:

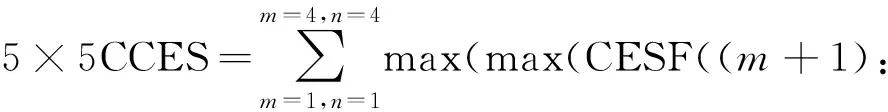
(m+3),(n+1):(n+4))))

(5)

为了方便量化处理后原信号的可识别能力,此处提出使用信号辨识度(Max-Mean-Dif)来作为标准,将其定义为拟合光子计数信号中最大值与均值的差值的对数,即:

Max-Mean-Dif=log10(Singlemax-Singlemean)

(6)

当采用不同维度的卷积核进行卷积时,卷积核为十字型,目的在于提取十字上的特征信息,其信号辨识度(Max-Mean-Dif)如图9所示,可以看出采用5×5的卷积核时效果相对来说最好,由于接收信号分辨率的限制,再增加卷积核维度也变化不大。

图9 不同维度卷积核对信号辨识度的影响Fig.9 The influence of different dimensional convolution kernels on signal recognition

采用5×5卷积核卷积后池化的信号仿真图如图10所示,可以看出已经出现了尖峰。

图10 采用5×5卷积核卷积后池化Fig.10 Pooling after convolution using 5×5 convolution kernel

空间卷积池化算法对于多通道累加算法的信噪比有一定优化,但不明显。由于卷积神经网络(CNN)已经发展趋于成熟,后续应采用神经网络算法训练出最合适的卷积核再讨论效果。

3.3 阵列拓展算法

阵列拓展算法是通过一定方法的阵列元素拓展,获得拓展矩阵,将新增矩阵组成的新矩阵和原始矩阵卷积运算,最后将逐帧信号取最大值组成解算信号。

如图11所示,原始矩阵(a)拓展得到(b)、(c)、(d)三种新矩阵,拓展方式为取相邻阵元的均值。将矩阵A、B、C、D卷积,后取最大值可得到解算信号:

S=max(max(A*((C×B)×D)))

(7)

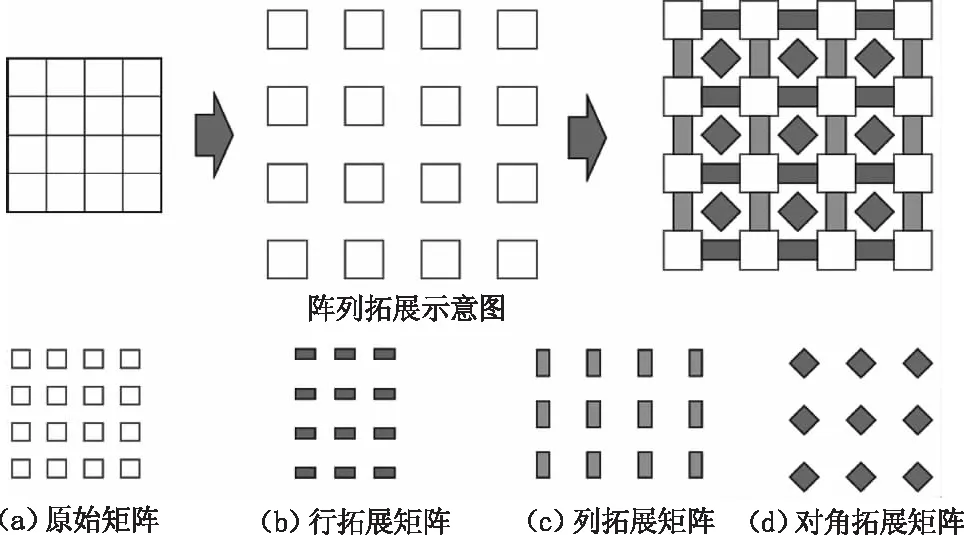
图11 阵列拓展示意图Fig.11 Illustration of the array expansion algorithm

其中,A、B、C、D分别对应图8中的(a)、(b)、(c)、(d)四种矩阵；max(max())操作可以取得矩阵最大值；×表示矩阵叉乘运算；*表示卷积运算。解算后的信号如图12所示。

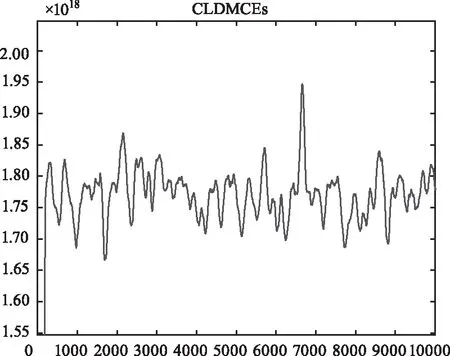
图12 阵列拓展算法信号处理仿真图Fig.12 Simulation results of the array expansion algorithm

3.4 信号辨识度

上文中采用了多通道累加算法、最大池化算法、空间卷积池化算法和阵列拓展算法的图6、图8、图10、图12的信号辨识度分别对应于图13中的allES16、allES、5×5CCES、CLDMCEs。

图13 信号对比度Fig.13 Signal contrast

4 总 结

盖革模式APD的信道阻塞问题一直是影响这一类型探测器件应用的难点问题,本文采用的三种基于光子计数法衍生的阵列算法可以很好地辨识出激光测距激光信号的回波时刻。

根据结果可以发现,三种方法都能够提升信号辨识度,采用了阵列拓展算法后的信号辨识度最高,空间卷积池化算法次之,两种方法均超过了多通道累加算法的效果。其中最大池化算法仅用于参考,可以发现效果相对最差的累加算法也实现了相对于最大池化算法的两倍增益。但是,空间卷积池化算法和阵列拓展算法均进行了大量的卷积,其复杂度远大于多信道累加算法。

综上所述,多通道累加算法最简便,硬件实例化时占用的资源最少,但效果不够明显,原因在于没有进行对噪声信号的预处理；空间卷积池化算法可以对不同散布特征进行一定区分,但运算量大；阵列拓展自适应算法对信号的辨识度最大,计算相对空间卷积池化算法略复杂,硬件实例化后占用资源较多,但提出了一种结合了前两种方法的通用计算方法,不需要在实际应用中耗费资源寻找合适的卷积核。同时可以对其中参数进行优化,添加适当的反馈,其中还有很大的研究空间。