基于伪谱法的城轨列车虚拟编队优化控制
2022-06-09张熠雯李树凯杨立兴
张熠雯,李树凯,杨立兴
(北京交通大学,轨道交通控制与安全国家重点实验室,北京 100044)
0 引言
随着城市轨道交通出行需求不断增大,城市轨道交通在大客流及多变环境下面临巨大的客运压力[1-2]。车车通信等技术不断发展,列车虚拟编队具有列车速度趋同,运行间隔距离小的特征,有效提高了列车既有运行线路的空间利用率。此外,基于满足高实时性要求的列车虚拟编队控制策略,虚拟编队可通过列车的灵活组编及解编实现车流及客流间更好的匹配,使城市轨道交通列车资源得到充分利用。因此,研究基于虚拟编队技术的列车控制方法对推动智慧城市轨道交通相关技术及运营管理方法的理论发展及应用落地具有重要的实际意义。
虚拟编队的概念最早在2000 年左右被提出[3-4],但该领域的进一步研究受到了相关技术的限制。近年来,随着车车通信技术不断成熟,虚拟编队应用于轨道交通系统成为一种可能,学者们对虚拟编队技术的可行性和虚拟编队模型等展开了进一步研究。2014 年,欧盟通过S2R 研究计划,并在先进运输管理与控制系统创新计划中提出“虚拟挂联”相关技术的研究与应用[5];Joelle等[6]从多个角度分析了虚拟编队及移动闭塞的相关表现;Nold等[7]分析了虚拟编队列车对基础设施和车载设备的需求及兼容性;Schumann[8]研究了不同情况下列车虚拟编队的运行模式;荀径等[9]建立了列车跟驰模型;Cao 等[10]设计了一种控制器并结合混合人工势场法协同控制虚拟编队列车;刘俊囡[11]设计了列车协同优化方法及列车协同延误方法。现有文献探究了虚拟编队技术的理论及优势,并研究了虚拟编队列车运行模型,但对于列车虚拟编队控制策略,仍缺少相关研究。
为实现虚拟编队追踪运行目标,列车追踪运行曲线的实时计算也至关重要。对于列车运行控制算法,相关学者对该领域已开展了大量研究。Goverde 等[12]对比分析了最大值原理和伪谱法求解列车最优控制问题;Gu 等[13]基于非线性规划方法提出了一种实时更新的列车节能运行控制策略;Liu 等[14]以节能、准点及乘客舒适度为评价指标,提出了一种改进的多目标粒子群算法求解基于移动闭塞的高速列车运行曲线;Felez 等[15]采用动态规划计算列车虚拟编队参考曲线;Li等[16]提出了一种基于交替乘子法的高速列车最优控制方法;Zhou 等[17]针对扰动下的高速电力列车,设计了一种具有双环结构的实时最优控制算法。现有文献对传统优化控制策略下列车运行追踪曲线优化进行了大量研究,但虚拟编队技术下列车运行轨迹需满足动态生成及实时调整的需求。因此,针对虚拟编队技术的列车优化控制策略需展开进一步研究。
基于对上述文献的讨论,考虑虚拟编队内各列车优化目标及安全约束,本文建立了列车虚拟编队最优控制模型。为实现虚拟编队内各列车追踪运行曲线的在线生成与调整,本文采用MPC 算法作为算法框架,将各采样点下的最优控制问题转化为多阶段最优控制问题,并采用伪谱法进一步将其转化为离散的NLP 问题求解。通过求解一系列最优控制问题,最终得到列车最优控制序列。最后,对本文提出的模型和方法,结合北京地铁昌平线进行了仿真与分析。
1 问题描述与建模
1.1 问题描述
根据编组计划,传统列车编组按照一定的编挂次序、编挂结构等通过机械挂联的形式将多车辆联结。而虚拟编队采用无线车车通信技术将多辆列车联结,使各列车以虚拟耦合的形式同步移动。各列车具有较高的自主性,且构成虚拟编队的多辆列车可看作单列车编队运行。为达到“编队”要求,在满足安全约束的条件下,虚拟编队内列车在运行过程中速度应尽可能保持一致,间隔距离应尽可能小。
本文研究的每个虚拟编队由n(n≥2)辆列车组成。图1 为列车虚拟编队示意图。编队内列车可分领导列车及跟随列车:领导列车是编队内第一辆列车;跟随列车是编队内领导列车所有后行列车的集合。列车虚拟编队采用分布式控制。分布式控制通过设置车载控制器来负责编队内各跟随列车运行轨迹,仅需考虑该列车及其前行列车运行状态。此外,领导列车运行轨迹由控制中心计算得到。与集中式控制相比,分布式控制降低了计算空间及时间的复杂度,更易满足多列车虚拟编队的高实时性协同控制。

图1 列车虚拟编队示意图
为实现小间隔距离的多车运行,虚拟编队技术采用相对制动模式进行制动。当列车紧急制动时,虚拟编队内的后行列车可根据前行列车所传输的速度、位置等相关信息进行制动,从而实现相对制动模式下的列车安全防护。而传统移动闭塞采用绝对制动模式进行制动。绝对制动模式下,基于前行列车传递的位置信息,通过令后行列车在到达该位置前完全制动来保证列车运行安全防护距离。当列车虚拟编队面临通信失灵等特殊情况或处于较大坡度等特殊路段时,虚拟编队内列车发生解编,即不再作为一个“虚拟编队”运行,此时,解编后的列车基于移动闭塞技术以绝对制动模式优化控制列车速度轨迹。
基于虚拟编队技术,设计列车虚拟编队优化控制策略,实时生成列车虚拟编队追踪运行曲线,发挥虚拟编队技术优势,进一步提升城市轨道交通运输能力。为建立虚拟编队列车最优控制模型,本文作出以下假设:
(1)站台长度满足多列车停站需求,列车自动控制系统满足信息传输高实时性要求。
(2)多列车虚拟编队运行于单条线路,不考虑运行过程中虚拟编队内列车在线路交叉处的组编及解编。
(3)忽略列车在运行过程中由天气、客流等因素引起的相关约束扰动。
1.2 参考速度曲线的最优控制模型
为构建列车给定运行区间内最优控制模型,以时间t为独立变量,速度v和位置s为状态变量,控制力u为决策变量,并将列车作为质点,根据牛顿运动学定律,可得到列车运行动态方程:
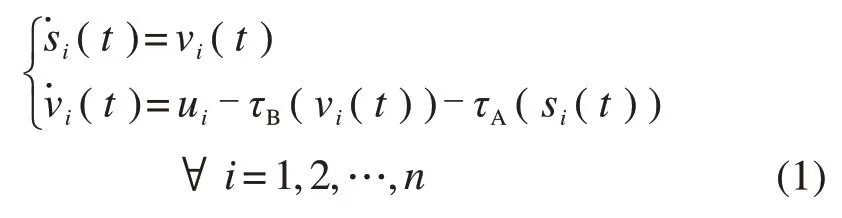
式中:i=1时,表示领导列车,i=2,3,…,n时,表示跟随列车;ui为列车i的控制力;τB(vi)为列车i的单位基本阻力,该值取决于列车运行速度;τA(si)为列车i的单位附加阻力,该值取决于列车运行线路条件。
单位基本阻力及单位附加阻力可通过下式计算得到:
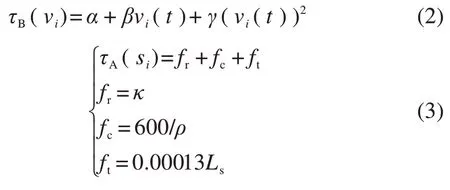
式中:α、β、γ为基本阻力系数;fr为坡度阻力;fc为弯道阻力;ft为隧道空气阻力;κ为轨道坡度的千分数;ρ为弯道曲率半径;Ls为隧道长度。
列车受到的控制力约束为:

式中:ui,min为列车i的最大制动力,为负值;ui,max为列车i的最大牵引动力,为正值。
在列车实际运行过程中,列车运行受到最大允许速度的限制,最大允许速度与列车运行的线路条件有关。因此,列车运行的速度约束如下所示:

式中:vi,max(s(t))为列车i在时间t时运行至某一位置所对应的最大允许速度。
列车在给定运行区间内运行,起点与终点位置确定,初始与终端速度都为0,则边界约束为:

式中:t0和tf为给定运行区间列车i的发车时间和到站时间;s0和sf为给定运行区间列车i的起点里程和终点里程。
为缩短发车间隔,提高既有线路运营效率,本文以最小化列车总运行时间为优化目标。因此,得到生成参考速度曲线的最优控制模型为:

式中:TTi为给定运行区间列车i的总运行时间。
该最优控制问题可采用最大值原理或伪谱法离线求解。
1.3 基于MPC框架的虚拟编队最优控制模型
MPC 算法将问题的有限时域分为若干子时域,各控制步骤下可得到预测时域Tp内的最优控制问题。基于滚动时域,结合实际情况不断更新列车的状态信息,重复计算一系列最优控制问题,最终可得到列车运行的最优控制序列。利用MPC算法,只需求解预测时域内的最优控制问题,减小了计算复杂度,且能够根据实况信息对初始输入值进行实时更新与动态反馈。
1.3.1 虚拟编队最优控制模型
根据列车参考速度曲线,设置列车运行时间区间为[T0,TH]。基于MPC 算法,对于给定运行区间,考虑列车虚拟编队实时控制要求,设置离散点[T0,T1,…,Th,…,TH],将区间运行时间离散为H个阶段,各阶段对应时间区间为[Th-1,Th],采样时间间隔为ΔT。不同阶段的相关参数及约束需根据各阶段初始状态信息、状态变量预测值以及最大限速曲线来确定。令当前采样点对应控制步骤为h。
在控制步骤h,输入列车状态信息初始值为:

对于预测时域端点,各列车状态变量受到边界约束:


此外,由于虚拟编队领导列车及跟随列车优化目标及需要考虑的安全约束有所不同,因此,领导列车及跟随列车具有不同的最优控制模型。
(1)领导列车最优控制模型
本文旨在通过虚拟编队技术缩短列车发车间隔,因此,对于领导列车i=1,给定参考速度曲线,令领导列车追踪参考速度曲线运行。在控制步骤h,预测时域内领导列车最优控制模型为:
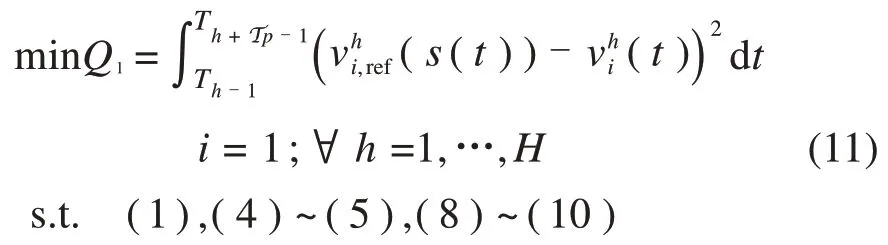
(2)跟随列车最优控制模型
对于跟随列车i=2,3,…,n,由于跟随列车需根据前行列车状态信息实时追踪运行,因此,在控制步骤h,跟随列车应考虑的安全距离约束为:

式中:d0为相邻列车间的最小安全距离;和分别为在控制步骤h,列车i的前行列车i-1 在上一控制步骤预测得到的预测时域终端时刻Th+Tp-1的位置及速度;Li-1为列车i-1 的长度。式(12)表示在预测时域内,相邻列车在运行过程中能够保证最小安全距离。式(13)表示当列车i-1 以最大制动加速度ai-1制动时,列车i以最大制动加速度ai进行制动,制动过程中任何时刻都能够满足安全距离,进一步保证了列车运行安全性。
跟随列车需在满足相关约束的条件下,追踪前行列车运行速度,减小与前行列车的间隔距离,使n辆列车组成一个有效的虚拟编队。因此,在控制步骤h,得到预测时域内跟随列车最优控制模型为:
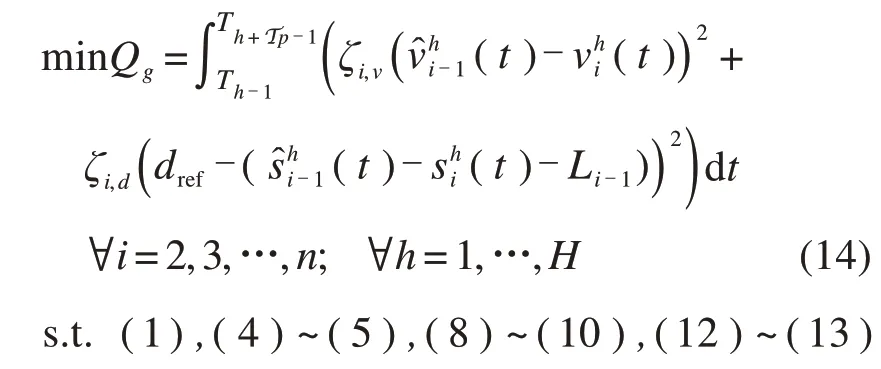
式 中:dref为相邻列车参考间隔距离为列车i与前行列车i-1 的实际间隔距离;ζi,v为列车i与前行列车i-1 间速度偏差的权重;ζi,d为参考间隔距离和相邻列车实际间隔距离偏差的权重。
1.3.2 闭环控制
在当前采样点,对应控制步骤h,给定列车运行状态初始值通过列车运行动态方程更新状态变量并求解预测时域Tp内的最优控制问题,可得到预测时域Tc内的列车最优控制序列及状态变量预测值将控制时域Tc内的列车最优控制序列应用于列车控制系统,并结合实际情况更新下一控制步骤h+1 的列车初始状态信息,由此完成一次闭环控制。基于滚动时域,求解一系列预测时域内的最优控制问题,可得到运行区间有限时域的列车最优控制序列。MPC框架下列车最优控制过程如图2所示。
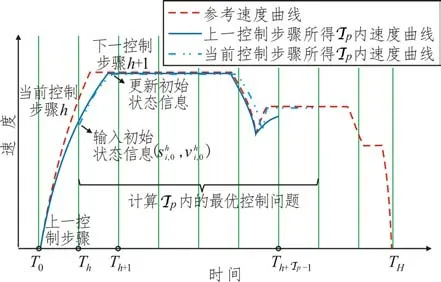
图2 基于MPC框架的列车最优控制示意图
2 算法求解
考虑列车运行区间内不同阶段下参数或约束不同,因此,预测时域内的最优控制问题可转化为多阶段最优控制问题。对于多阶段最优控制问题,可采用伪谱法进行求解。
Radau 伪谱法(RPM)利用Legendre-Gauss-Radau(LGR)配置点对各阶段进一步离散得到多个子阶段,并采用全局插值多项式近似最优控制问题的状态变量、控制变量以及协态变量,从而得到离散的NLP问题并进行求解[18]。RPM 具有较高的精度及计算收敛速度,在实时优化控制方面具有广泛的应用前景[19-20]。
2.1 多阶段最优控制问题
基于1.3 内容,将区间运行时间离散为H个阶段。在控制步骤h,第k个阶段所对应的区间为[Tk-1,Tk]。为便于模型中符号的理解,将其表示为,k=h,…,h+Tp-1。则在控制步骤h的第k个阶段,列车运行动态方程(1),路径约束(4)、(5)和(11)可重构为:

与安全距离相关的预测时域终端约束(13)可转化为如下形式,该约束也称作事件约束:

此外,第k个阶段的边界约束为:
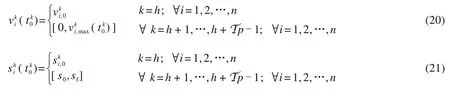

式(20)、(21)表示预测时域内第k个阶段列车i的状态变量初始约束。在当前控制步骤h,初始值为输入值。式(22)、(23)为预测时域内第k个阶段列车运行速度及位置的终端约束。
此外,为保证预测时域内各阶段列车状态变量的连续性,考虑如下连接约束:
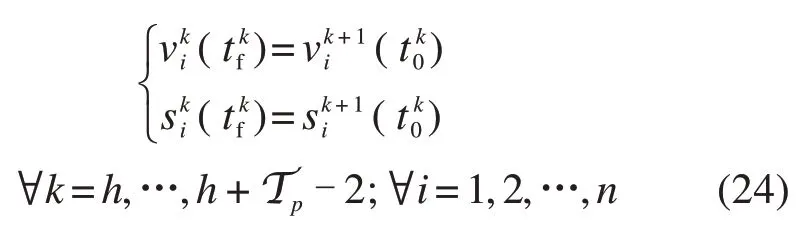
综上所述,在当前控制步骤h,预测时域内领导列车的多阶段最优控制模型为:

以及当前控制步骤下预测时域内跟随列车的多阶段最优控制模型为:

2.2 Radau伪谱法
首先,对于预测时域内第k个阶段,对独立变量进行转化:

式中:ξ为新的独立变量,且由式(27)可知,ξk(t)∈[-1,1]。
则t(ξk)可由下式表示:
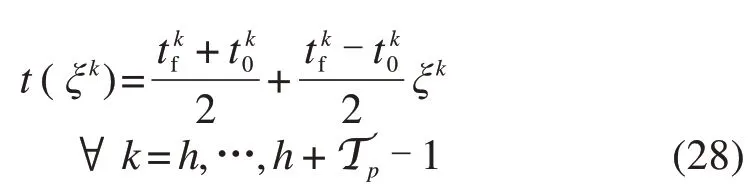
令列车i第k个阶段的状态变量列车运行动态方程则基于R+1 个LGR 配置点可采用全局拉格朗日插值多项式近似状态变量
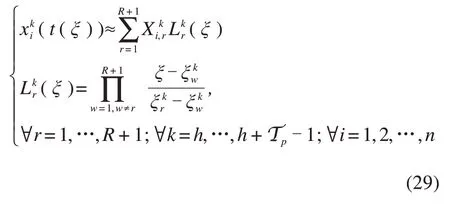
基于离散后状态变量及控制变量在各配置点的数值近似,第k个阶段的列车运行动态方程(15)可由多项式的微分近似表示:
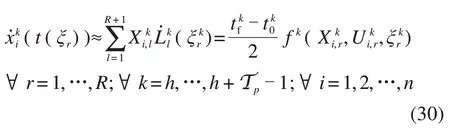
此外,在控制步骤h的第k个阶段,领导列车及跟随列车所包括的路径约束(16)~(18)转化为:

同样地,事件约束(19)重构为:

边界约束(20)~(23)可转化为第1 个和第R+1个配置点的约束:
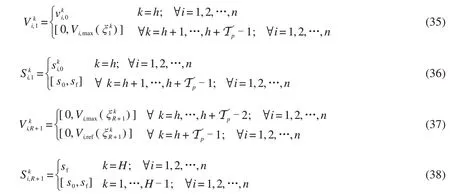
各阶段间的连接约束(24)转化为以下形式:
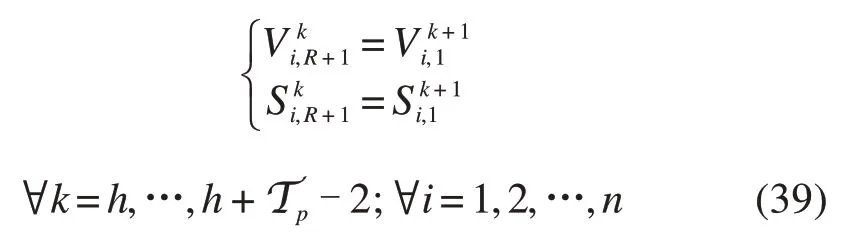
综上所述,将预测时域内领导列车最优控制模型离散并转化,得到如下NLP问题:

同样地,预测时域内由配置点离散得到NLP形式的跟随列车最优控制问题为:
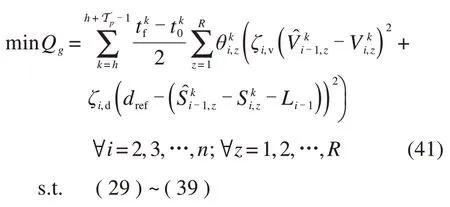
2.3 算法流程
基于上述内容,求解MPC 框架下基于伪谱法的列车虚拟编队最优控制问题主要算法流程图如图3所示。

图3 基于伪谱法的列车虚拟编队最优控制问题算法流程图
3 仿真验证
3.1 算例描述
以北京昌平地铁线全线为例,依据11 个运行区间相关数据,设置地铁列车虚拟编队运行的基本场景进行仿真验证。对于由多辆列车组成的虚拟编队,除领导列车外,各列车同其前行列车的最优控制模型与方法和领导列车及其后一辆跟随列车所采用的最优控制模型与方法一致。因此,本文以2 辆地铁列车组成的虚拟编队为例进行建模与分析。与此同时,为验证本文所提出的列车虚拟编队最优控制模型与方法对于提升既有线路运输能力的有效性,本节对比了虚拟编队相对制动模式及传统移动闭塞绝对制动模式下跟随列车对领导列车的追踪运行效果。
此外,由于缺少地铁列车实际的车型及运行参数,因此对相关参数进行假设,在工程应用当中可根据实际需要调整相关参数数值。设置模型中相关参数如表1所示。

表1 模型参数
基于线路最大允许速度和模型相关参数,以最小化列车总运行时间为优化目标,离线计算得到领导列车及跟随列车的参考速度曲线如图4所示。
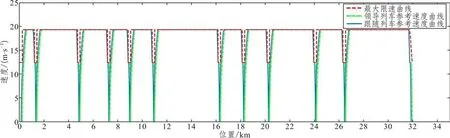
图4 地铁列车最大限速曲线及参考速度曲线
3.2 结果分析
在操作系统为Windows 10,CPU 为Intel(R)Core(TM) i5-6300HQ CPU,运行内存为4.0GB 的64 位计算机上,调用MATLAB R2020a GPOPS 对地铁列车虚拟编队最优控制问题进行仿真验证。
当ζv:ζd=1 时,分别求解虚拟编队领导列车和相对制动模式及移动闭塞绝对制动模式下跟随列车追踪运行曲线,仿真结果如图5(a)~(d)所示。


图5 虚拟编队领导列车及跟随列车运行曲线
由图5(a)、(b)和(c)可以看出,虚拟编队相对制动模式下跟随列车与领导列车的速度曲线几乎保持相同,且与领导列车相比,跟随列车可在无时间延迟的条件下到达运行终点。对于移动闭塞,跟随列车的速度曲线在初始加速阶段及制动阶段存在波动,且该制动模式下列车的平均运行速度小于领导列车及虚拟编队相对制动模式下跟随列车的平均运行速度。因此,绝对制动模式下跟随列车到达运行终点具有较大的时间延迟,达101.0 s。此外,由图5(d)可以得到,虚拟编队相对制动模式下地铁列车最大运行间隔距离为65.48 m,显著小于绝对制动模式下地铁列车最大运行间隔距离231.86 m。因此,与移动闭塞绝对制动模式相比,相对制动模式下地铁列车虚拟编队具有更短的运行间隔距离和到达运行终点的时间延迟,有效提高了既有线路的空间利用率。此外,求解预测时域内最优控制模型所需时间为0.10~1.01 s,平均运行时间为0.287 s,小于控制时域Tc 对应的时间周期2 s,满足列车虚拟编队最优控制的实时性要求。
此外,不同权重比下跟随列车追踪运行曲线不同,如图6 所示。在领导列车开始减速之前,不同权重比下的跟随列车具有相同的运行曲线。这是由于在当前考虑的既有线路条件下,根据最大允许速度曲线及计算得到的参考速度曲线,在满足相关约束的条件下,跟随列车以其最大运行速度行驶,可同时满足速度追踪偏差及运行间隔距离最小。因此,当前条件下权重比不影响这一阶段内跟随列车的追踪运行曲线。当领导列车进入减速区间,不同权重比下虚拟编队相对制动模式所生成的跟随列车运行追踪曲线不同。ζv:ζd=1000 时,跟随列车与领导列车间的最小运行间隔距离为22.00 m;ζv:ζd=1 时,跟随列车与领导列车间的最小运行间距为12.69 m。权重比越小,跟随列车开始制动的时间越迟,对应阶段跟随列车与领导列车间的间隔距离越小,区间内列车的运行时间越短,相应地,以领导列车达到运行终点的时间为基准,跟随列车到站时间延迟也减小。由此可知,随着权重比减小,跟随列车追踪领导列车组成虚拟编队的整体性有所降低,但既有线路的运输能力略有提高。同时,由于列车运行间隔距离小,对列车的安全性要求也更高。

图6 不同权重比下虚拟编队跟随列车运行追踪曲线(区间1)
4 结束语
对于城市轨道交通列车虚拟编队问题,具有实时性的列车运行优化控制策略至关重要。本文以最小化列车总运行时间为优化目标,构建了列车虚拟编队参考速度曲线最优控制模型。针对领导列车及跟随列车,构建了两类MPC 框架下的列车最优控制模型以及多阶段最优控制模型,并采用RPM 将多阶段最优控制模型进一步离散得到NLP 问题进行求解,得到实时生成及动态调整的城市轨道交通列车虚拟编队运行追踪曲线。以北京地铁昌平线为例,验证了本文提出的城市轨道交通列车虚拟编队优化控制策略能够显著提升既有线路的运输能力。本文针对高速小间隔下运行的虚拟编队列车,设计了一种能够满足高实时性要求的列车优化控制策略,为智慧城市轨道交通运营的智能控制技术发展提供了方法支撑,具有重要的实际应用价值。
此外,本文只考虑了单条线路及确定性列车动态模型下的列车虚拟编队优化控制策略,对于复杂线路网络以及复杂运行条件下如何针对具有不确定性的列车虚拟编队系统来设计优化控制策略需展开进一步研究。
