基于分级思想的微电网重构优化研究

简吟雪，郭诗书，李国平

（1.三峡大学湖北省微电网工程技术研究中心，湖北 宜昌 443002；2.国网湖北省电力公司咸宁市供电公司，湖北 咸宁 437000；3.湖北能源鄂州发电有限公司，湖北 鄂州 436000）

0 引言

由分布式电源、储能装置、逆变器等装置组成的微电网可并网运行，可孤岛运行。当其并网运行时，通过公共连接点（Point of Common Coupling，PCC）节点来保证微网系统功率平衡；当微网系统故障，其处于孤岛运行时，断开PCC 节点利用孤网内部的可控微源保证功率平衡，此时需进行微网重构优化，重构后的微网系统具有网损低、系统稳定等优点。

目前微电网重构时，需要考虑系统的重构组网规则。文献［1］提出了一种同时包含重构与孤岛划分的故障恢复方法。文献［2］提出了一种综合考虑网络重构与孤岛划分的故障恢复运行策略。文献［3-4］阐述了孤岛运行时可以由可控微源来支撑系统的频率和电压。

现有研究认为当微网系统故障时，为让系统能够快速达到新的稳定，应充分考虑故障微网重构约束条件，建立相应模型并优化，获取最优重构方案。一般情况下，故障微网重构时建立的综合适应度函数，多采用算法进行寻优。文献［5-6］利用多代理技术对故障微电网进行优化重构，该技术算法不需迭代计算且实用性好，但结果不是最优。文献［7］引入粒子群算法来解决故障微电网重构优化的问题，但粒子群算法效率低且参数设置不当会影响其稳定性。文献［8-10］对故障微电网进行重构时，若系统参数设置、目标函数都比较理想，遗传算法优化可取得较好的寻优结果，但由于其需要进行潮流计算，因此寻优效率低下。

对故障微网进行重构优化时，部分智能算法需进行潮流计算，导致其寻优效率低且结果不精确。本文采用分级优化法对故障微网进行重构优化，获取精确的优化结果。分级优化法是对数学模型进行分级优化求解，可让问题变得更简单，求解速度更快且结果更精确。文献［11］在蚁群智能算法中引入分级优化思想，对多目标优化问题进行拆分分级优化处理，并获取最优结果；文献［12］为解决系统风电波动问题，在系统控制策略中采用分级优化法进行优化控制，来解决系统风电随机性、波动性问题，提高可再生能源利用率。

在分级优化研究的思想下，考虑在系统负荷率最大及系统网损最小目标下，对故障微网进行重构优化的问题。首先，考虑故障微网重构的约束条件及系统的组网规则；其次，建立故障微网重构的数学模型；最后，运用分级优化的算法对故障微网重构的问题进行分级优化处理，以最少计算时间、最快计算速度，得到最优的重构结果，并验证模型的合理性与正确性。

1 微网系统重构约束及优化

1.1 微网系统重构约束

若微网系统发生故障，微网会自动切换至孤网状态，此时微网重构需系统内可控微源保证其稳定运行。微网系统故障时，系统进行稳定重构需要考虑以下因素：独立微网系统的电压、频率稳定因素，独立微网系统的功率平衡因素，独立微网系统内各种负荷的功率需求因素，以及微源配置因素等。因此，在考虑微电网系统重构约束的基础上，提出系统多目标优化重构方案，对故障微网进行优化重构。

（1） 微网系统重构时的微源配置。

系统微源分为可控及不可控两类，微网重构主要考虑由可控微源配置来支撑孤网电压、频率。目前光伏发电和风力发电的间歇性、随机性较大，且输出功率受环境制约，造成其不能为系统输出稳定功率，不具备承担微网重构所需的电源特性。因此，需要使用具有调节性，可保证系统电压、频率稳定的电源对微网重构进行组网。目前，微网重构选择可控微源燃气轮机作为组网的分布式电源（Distributed Generation，DG），而不可控微源作为并网DG，并为负荷提供功率支撑。

（2） 微网系统重构时的微源、负荷间配置。

系统中的负荷可以分为重要负荷和不重要负荷，重要负荷要保证其不间断供电，不重要负荷在保证微网稳定运行的前提下进行切换。微网进行重构后，组网DG 提供系统中重要负荷功率，根据微网功率分配尽可能保证不重要负荷的功率需求。

1.2 微电网重构优化思想

对微电网重构进行多目标优化时，需考虑相关约束条件、目标函数等因素，如系统重构时的优化速率，系统重构时网损最小并满足最大的负荷需求等。在本文提出的分级优化法中，第一级优化是无潮流计算寻优，第二级优化是有潮流计算寻优。先进行无潮流计算的第一级寻优，相关指标满足后方可进入有潮流计算的第二级寻优，可在最短时间得到最优重构方案，不仅优化速率快，且得到的故障微网的重构方案更精确。

2 系统重构的数学模型

本文把系统功率损耗及系统网损成本最低设为目标函数，考虑相应约束条件并建立优化模型。

2.1 目标函数

（1） 系统功率损耗。

式中，P为系统功率损耗，m为系统第m条支路，lm为系统第m条支路的重构状态，N为系统重构支路数，Pm、Qm和Rm分别为支路m的有功功率、无功功率和电阻，Um为系统支路m的末端电压。

（2） 系统网损成本。

式中，C为系统网损总成本；d为系统实时电价，一般是0.58 元/(kW ⋅h)。

2.2 系统重构的约束条件

（1） 系统重构的节点电压约束。

式中，Ua_max、Ua_min为节点a处的电压上、下限。

（2） 系统重构的支路功率约束。

式中，PSl_max为支路l的功率上限。

（3） 系统重构的微源容量约束。

式中，PSG为系统负荷功率，PSG_max、PSG_min分别为系统微源的功率上、下限。

3 优化算法

3.1 故障微网系统重构的分级优化算法

由于一般智能算法满足不了本文微网重构优化要求，因此本文提出分级优化算法获取最优解，主要步骤是：首先，减少潮流计算次数，提高故障微网重构优化速率；然后，对目标函数进行优化并求出最优重构结果。故障微网系统重构的分级优化思想如下：

（1）第一级优化，不考虑潮流计算进行优化。若系统处于离网工况，根据系统功率需求动态切换系统负荷，选取负荷连接开关并编号，利用遗传算法得到满足微网发电量范围的开关集合DL、对应负荷功率解集PSG，利用第二级优化得出最终结果。

（2）第二级优化，在考虑系统功率损耗、负荷功率等需求进行潮流优化计算。对优化解集D开关进行排列，并得到多个解集Dm；对负荷集合中DL开关集合进行优化，得到集合Dn并求其网损最小组合，不需再优化重构。若负荷集合没有在DL求出合适解，则继续进行优化求解，直到得出最优重构结果，将无效解并入Dz集合中。若负荷集合中没有得出最优重构结果，则重新重构直到获取最优结果为止。

3.2 故障微网系统重构的分级优化算法步骤及流程图

算法流程如图1 所示，优化算法步骤如下：

图1 算法流程图Fig.1 Flow chart of algorithm

（1）数据输入。

（2）通过系统负荷开关进行拓扑搜索，得到系统负荷总功率PS，得到满足要求的开关组合DL及负荷功率集合PSG。

（3）在DL中求出最优开关集合D。

（4）将PSG中负荷功率进行排序，得x。

（5）对PSG中负荷功率进行循环，m∈[1，x]。

（6）在D集合中找到PSG(m)对应所有开关组合Dm。

（7）对Dm进行潮流优化，求出相应数据。

（8）在Dm中求出最优开关集合Dn，及不符合优化条件的开关集合Dz。

（9）比较Dz系统损耗，选出最优解。若Dz不符合要求，返回步骤（5）重新优化；若Dz满足条件，则求出最优解，结束算法流程。

（10）如果步骤（5）至循环结束，仍然找不到最优解，表明故障微网不能重构。则在Dz开关集合中计算其Y值，取其最小值为系统重构解，并输出结果。其中Y的表达式如下：

式中，Y为越限综合度，Y1、Y2为节点电压及支路功率越限综合度，w1、w2为加权系数。

4 仿真研究

本文以CERTS 微电网为基础模型，考虑微网系统的优化重构并对其进行仿真实验，该系统的电压等级是380 V，系统中有LD1、LD2、LD3、LD4、LD5、LD6 等6 个负荷，其功率为55 kW、25 kW、65 kW、25 kW、35 kW、65 kW，且系统功率因数为0.95。系统中可控微源燃气轮机输出功率70 kW，系统中不可控微源光伏电池、风机的输出功率是15 kW、25 kW，储能装置功率100 kW；线路电阻为0.17 Ω/km，电抗为0.08 Ω/km。其中可控微源作为系统平衡节点，负荷作为系统PQ节点，不可控微源作为系统PV节点，且系统重要负荷功率需求由可控微源保证，图2 是系统网络节点图。

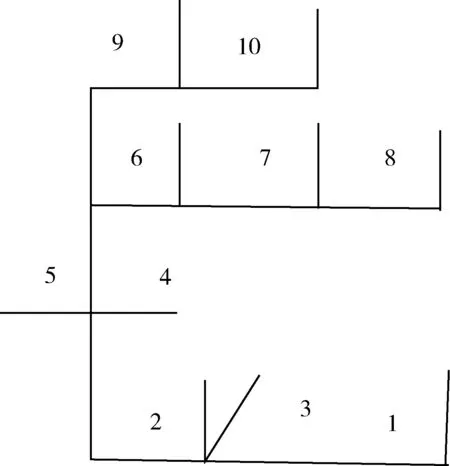
图2 系统网络节点图Fig.2 System network nodes chart

系统可控微源燃气轮机有功功率为70 kW，无功为45 kVar；系统节点电压约束为0.95～1.05；系统支路的有功功率及无功功率上限分别为160 kW、80 kVar。系统输出功率在160 kW～200 kW 范围内，不可控微源的无功输出小于2 倍的有功输出。若微网系统故障，PCC 节点断开时，微电网系统为离网模式运行，分别采取遗传算法及分级优化算法进行故障微网系统重构，并对两种算法的仿真结果做对比分析。本文采取的遗传算法染色体长度为16，种群规模为20，遗传代数是60 代，变异概率为0.1，交叉概率0.5；分级优化算法的步骤如3.2 节所示。

表1 和表2 是用遗传算法对故障微网系统进行重构得到的仿真结果。虽然表1 和表2 微网系统的负荷最优解相同，但表1 的系统损耗更低，表明表1 的重构结果更好。

表1 系统重构结果1Tab.1 Reconstruction system results 1

表2 系统重构结果2Tab.2 Reconstruction system results 2

采用分级优化算法对微网系统进行算例仿真分析，表3 表示微网系统重构的第一级优化结果，表4 表示微网系统重构的第二级优化结果，且用分级优化多次重构后得到的测算结果相同。

表3 系统重构的第一级优化Tab.3 First level optimization of system reconfiguration

表4 系统重构的第二级优化Tab.4 Second level optimization of system reconfiguration

由表3 和表4 可知，经第一级优化后，系统负荷功率在165 kW～195 kW 之间时满足要求，负荷量超过微电网系统输出功率上限200 kW 的开关组合都被淘汰。由第二级优化结果可知，有2 组开关组合的负荷功率分别为195 kW 和175 kW，其平衡节点有功功率为72.5 kW 和78.5 kW，均超过可靠微源燃气轮机输出功率上限70 kW，因此淘汰。但负荷功率为185 kW 的开关组合仍然满足要求，可得最优开关组合为［1001 1101 1110 1110 11］。

表5 为系统重构最优结果，系统最终得出的最优重构解的计算时长为0.345 s，支路最大传输有功功率为94.5 kW、无功功率为44.5 kVar，节点电压最大值为1.00 p.u.，最小值为0.98 p.u.，均满足条件。

表5 系统重构最优结果Tab.5 Optimal results of system reconfiguration

根据以上仿真分析可知：

（1）在稳定性上，分级优化算法优于遗传算法，且分级优化算法与遗传算法的重构结果相同；

（2）在计算效率上，分级优化算法的计算时长比遗传算法的计算时长更短。

若调整微网系统中节点电压约束，让其范围在0.98～1.10 之间，将造成微网系统重构失败。表6 就是其重构结果，并取w1=0.45、w2=0.55 来计算越限综合度Y。

表6 系统越限信息Tab.6 System over limited results

由表6 的越限综合度Y值可知，开关组合［1001 1101 1101 1110 11］为微网系统的最优重构解，此时的负荷功率为185 kW。综上分析，分级优化算法计算速度更快、网损成本更低，系统运行经济性更强。

5 结论

当微网处于故障工况时，为让微网系统在最短时间恢复稳定可靠运行，需对故障微网系统进行重构。因此，本文对故障微网系统进行重构时，充分考虑了影响微网系统重构的约束条件，并建立故障微网系统的重构模型。充分考虑了微源容量配置，负荷功率需求，系统电压、电流、频率稳定，以及网损等关键性指标，采取分级优化思想对故障微网重构模型进行求解。最后，通过分析仿真结果验证故障微网重构模型正确性及分级优化算法的高效性。在仿真分析中，采用遗传算法与所提分级优化算法进行对比，有仿真分析结果可知，分级优化算法获得的最优解与遗传算法一致，且计算时长更短，仅为0.354 s。由仿真分析可知，分级优化算法不仅优化速度快，而且其求出的最优微网系统重构结果准确，验证了所提方法的有效性。