末敏子弹稳态扫描阶段运动特性研究

岳明凯，王程远 ，焦志刚，陈 伟

(1.沈阳理工大学 装备工程学院，沈阳 110159；2.辽沈工业集团有限公司，沈阳 110045)

坦克装甲车辆在现代地面战争中占据主导地位，反装甲任务日益加重，而具有较高效费比的末敏弹可以有效毁伤装甲目标[1-3]。

末敏子弹工作时以母弹为载体抵达目标上空，在规定高度从母弹中抛出，经过减速减旋后，张开主旋伞，并继续减速，直到达到稳定状态，此时伞-弹系统一边匀速下降，一边绕铅垂线匀速旋转[4]，达到末敏子弹扫描、识别目标的要求。

末敏子弹的伞-弹系统具有复杂的动力学特性，一直以来都是末敏弹稳态扫描运动特性研究的重点，其稳态扫描运动对末敏子弹识别、命中目标起到决定性作用[5-6]。张俊等[7]在牛顿力系下建立了伞-弹系统的运动模型，分析了各弹道诸元的变化规律；董严等[8]忽略了伞-弹间滚转运动的自由度，使用拉格朗日力学方法建立了伞-弹系统平面内运动模型；马宗成等[9]将伞与伞盘视为一个刚体，子弹视为另一个刚体，建立了伞-弹二刚体动力学模型。在伞-弹系统二刚体动力学模型中，通过球铰链连接的约束未必能符合其连接机构及约束类型，并且在二刚体模型中忽略了伞盘的运动情况。因此，为进一步准确描述末敏子弹稳态扫描阶段的运动状态，建立柱铰连接的伞-弹三刚体动力学模型十分必要。

本文将伞、伞盘、弹体视为刚体，伞盘与弹体之间通过柱铰连接，基于第二类拉格朗日力学方法推导出伞-弹系统稳态扫描阶段动力学方程组，并使用Adams软件进行仿真，验证伞-弹系统动力学模型的准确性。

1 末敏子弹稳态扫描阶段伞-弹系统模型

1.1 拉格朗日力学方程

本文采用第二类拉格朗日力学方程分析伞-弹系统运动特性，其方程为

(1)

(2)

(3)

式中：T为系统的动能；t为时间；qk为系统的广义坐标；Q为系统的广义力；k为系统自由度个数；n为组成系统的刚体个数；s为系统完整约束的个数；W为主动力所做的虚功；mi为质点i的质量；vi为质点i的速度；Ji为质点i的转动惯量；ωi为质点i的转动角速度。

1.2 模型假设

本文将伞-弹系统简化为弹体、伞盘和伞系统(伞和伞绳)三部分，并作如下假设：

(1)忽略主旋伞张开过程；

(2)将伞、伞盘、弹体视为刚体；

(3)伞与伞盘为球铰连接，伞盘与弹体为柱铰连接；

(4)忽略伞绳拉力及附加质量；

(5)稳态扫描阶段伞-弹系统速度较低，故忽略弹体和伞盘的空气动力影响。

1.3 伞-弹系统动力学模型

1.3.1 坐标系定义及广义坐标选取

为方便分析伞-弹系统的运动规律，建立如下坐标系。

(1)基准坐标系O-XYZ

抛撒点为坐标原点O，OZ轴铅垂向上，OY轴沿水平方向指向射向，OX轴由右手法则确定。该坐标系用于确定伞、伞盘和弹体的质心坐标。

(2)平动坐标系Oi-XiYiZi

原点Oi取刚体i质心Ci处，各轴方向同基准坐标系。该坐标系用于确定伞轴、伞盘轴、弹轴和速度方向。

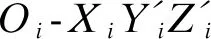
选取伞盘与弹体的连接点D的坐标(x,y,z)、主旋转伞的空间姿态角(θ,ψ,φ)、伞盘的空间姿态角(θ2,ψ2,φ2)以及弹体坐标系相对于伞盘坐标系转动的角度θd作为广义坐标，即k=10，q=(x,y,z,θ,ψ,φ,θ2,ψ2,φ2,θd) 。伞-弹系统结构如图1所示，图中la为伞绳长度，lc为子弹弹长，CA为主旋伞质心。

图1 伞-弹系统结构示意图

1.3.2 系统动能

将伞刚体质心坐标系平移到连接点D，则伞刚体质心坐标表示为(0，0，la)。通过坐标转换关系，可得到伞刚体的质心在基准坐标系下的坐标为

(4)

将式(4)对时间t求导，可得到伞刚体质心速度为

(5)

伞刚体角速度为

(6)

伞盘刚体质心坐标可认为与连接点D重合，故伞盘刚体质心坐标表示为(0，0，0)。伞盘刚体质心速度为

(7)

伞盘刚体角速度为

(8)

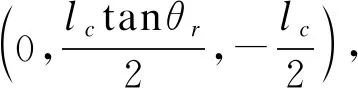
(9)

将式(9)对时间t求导，可得到子弹刚体质心速度为

(10)

同理可求得vcy和vcz。

子弹刚体角速度为

(11)

将式(4)～(11)带入式(3)可得到各刚体的动能，因此末敏子弹稳态扫描阶段的系统动能为

T=Ta+Tb+Tc

(12)

式中：T为伞-弹系统动能；Ta为主旋伞动能；Tb为伞盘动能；Tc为子弹动能。

1.3.3 系统广义力

作用在伞-弹系统上的力和力矩包括

G=mg

(13)

(14)

(15)

(16)

(17)

(18)

(19)

为区别于实位移，虚位移采用变分符号表示。伞-弹系统在x、y、z方向的虚位移可分别表示为δx、δy、δz，主旋转伞、伞盘及弹体的空间旋转角表示为δθ、δψ、δφ、δθ2、δψ2、δφ2、δθd。则伞-弹系统虚功为

∑δW=∑Fδq

(20)

式中F为作用在系统上的主动力。

以广义坐标θd为例，将式(20)带入式(2)可得系统广义力为

Qθd=θd(Mdycosθd+Mdzsinθd)-Mdzcosθd+

Mdysinθd

(21)

同理可将其他广义坐标带入第二类拉格朗日力学方程，求解得到末敏子弹稳态扫描阶段的动力学模型为

(22)

式中Ek、Fk、Gk、Hk为由拉格朗日力学方程求出的系数矩阵。

2 仿真计算及分析

本文基于拉格朗日力学方法，建立末敏子弹伞-弹系统三刚体动力学模型。为验证模型的准确性，在SolidWorks中建立伞-弹系统三维模型，并将其导入Adams软件中，设置刚体质量、材料、初速等参数，根据各刚体之间的接触和相互运动关系设置链接副与运动副，并添加广义力。在Adams软件中，设置好约束、接触、链接副和运动副的伞-弹系统模型如图2所示。

图2 Adams前处理设定完成模型图

计算中各参数取值为：伞质量ma=0.46kg；主旋伞特征面积S=1.77m2；伞特征长度l=0.8m；伞绳长度la=1.2m；伞盘质量mb=0.1kg；弹体质量mc=10.85kg；弹长lc=0.225m；初始下落速度v=50m/s；静悬挂角θ0=22.5°。仿真得到末敏子弹速度随时间的变化如图3所示，末敏子弹高度随时间的变化如图4所示，末敏子弹转速随时间的变化如图5所示，末敏子弹扫描角度随时间的变化如图6所示。

图3 伞-弹系统速度随时间变化曲线

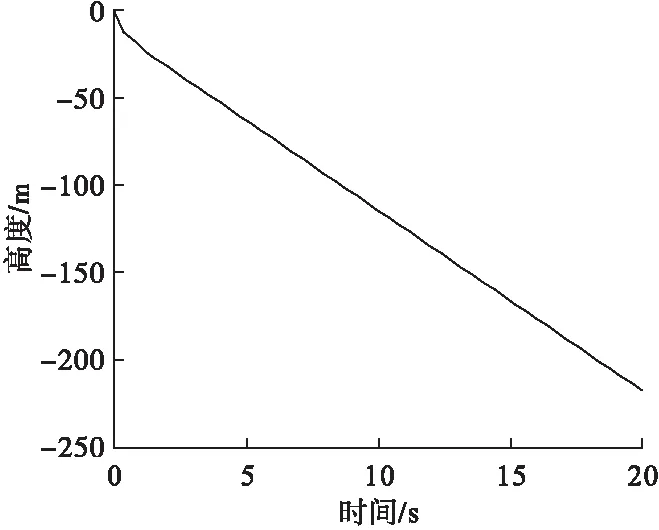
图4 伞-弹系统高度随时间变化曲线

由图3可见，伞-弹系统在主旋转伞张开后，速度迅速降低，经过3.6s后，系统重力、空气阻力、空气升力达到平衡状态，系统加速度降为零，此时系统匀速下降，落速稳定于10.29m/s。

由图4可见，伞-弹系统在20s内高度下降了217m，且在伞-弹系统落速稳定后，系统下降高度和时间成正比。

图5 伞-弹系统转速随时间变化曲线

由图5可见，在空气导转力矩的作用下，伞-弹系统转速在初始0.4s内迅速增大至7.7r/s，之后受伞极阻尼力矩的影响，转速开始下降，在4.4s稳定于4.04r/s。相较于系统落速，系统转速进入稳定状态多用时0.8s，这是由于伞极阻尼力矩和空气导转力矩均与速度有关，只有在下落速度达到稳定状态以后，转速才会逐渐达到稳定状态。

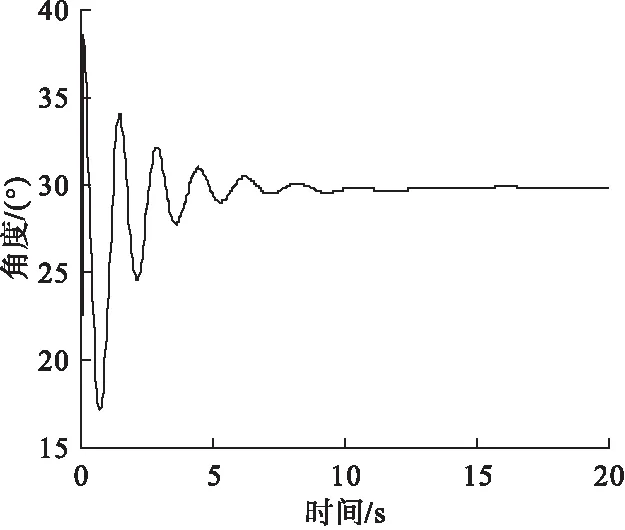
图6 伞-弹系统扫描角度随时间变化曲线

由图6可见，系统扫描角度在初始阶段波动较大，经过5s后波动减小并逐渐趋于稳定，最终在 7.5s左右稳定于29.8°左右。这是由于弹体与伞盘之间为柱铰连接，存在摆动自由度，落速及转速变化会使弹体发生摆动，在主旋转伞张开后，系统落速及转速变化较大，故系统扫描角度波动也较大，当系统速度和转速稳定后，扫描角最终进入稳定扫描状态。

伞-弹系统稳态扫描阶段的下落速度一般为10～20m/s、转速为4～10r/s[10]，故仿真结果与实际情况相符，建立的动力学模型准确可靠。

3 结论

采用第二类拉格朗日力学方法，建立了伞-弹系统三刚体动力学模型，并使用Adams软件进行仿真，得到以下结论：

(1)在主旋转伞完全张开后，伞-弹系统的下落速度在3.6s后稳定于10.29m/s，转速在空气导转力矩的作用下，先迅速增大至7.7r/s，随后由于伞极阻尼力矩的影响在4.4s稳定于4.04r/s，扫描角进入稳定状态用时最长，在6s稳定于29.8°，20s内系统高度下降217m，符合末敏子弹稳态扫描阶段的运动规律；

(2)在由伞、伞盘、弹体构成的三刚体模型中，伞与伞盘之间采用球铰连接、伞盘与弹体之间采用柱铰连接，与传统拉格朗日力学方法相比，考虑了伞盘的运动特性，提高了伞-弹系统稳态扫描阶段动力学模型的准确性。