基于一致性算法离网系统分层控制
2022-06-09翁玮钰李国平郭诗书
翁玮钰,李国平,郭诗书
(1.三峡大学 湖北省微电网工程技术研究中心,湖北 宜昌 443002;2.湖北能源鄂州发电有限公司,湖北 鄂州 436000;3.国网湖北省电力有限公司咸宁供电公司,湖北咸宁 437000)
0 引言
由于传统供电方式可靠性难以满足系统负荷需求,分布式发电供电灵活且可靠稳定,因此应用广泛。微电网系统通过公共连接点(Point of Common Coupling,PCC)自由切换与大电网相连的状态,并网运行时系统电压、频率由大电网支撑;离网运行时系统自治,可保证电压、频率稳定[1]。由于离网系统易受外界干扰,系统可靠性变差,因此研究其可靠控制具有重要意义。
文献[2]学者以下垂控制为基础,研究微网系统中线路阻抗不能忽略,其分布式微源无功出力是否按照下垂控制系数进行分配。文献[3]在下垂控制中引入了负荷侧电压幅值对系统无功进行精确分配,但不能消除电压、频率的影响。文献[4]在下垂控制系统中引入无功功率偏差项计算有功扰动项,对系统分布式微源进行调节控制实现其无功的均分。文献[5]提出了分层控制策略,如第一层采取传统控制,第二层解决第一层控制引起的系统功率、电压和频率问题,保证系统安全可靠运行。文献[6]提出了基于一致性算法实现系统的局部通信的方法,并合理地控制了系统电压、电流,其通信负担小、可靠性高。
当微网系统并入各种负载后,会引起系统运行可靠性降低的问题。文献[7-8]采取对称分量法分离系统逆变器输出的正序及负序电压,再调节系统正序、负序电压,实现系统分布式微源的容量分配。文献[9]在不平衡工况下,采取虚拟同步发电机平衡电流控制法,降低功率振荡,并对系统不平衡电流进行控制。文献[10]在不平衡负荷控制策略下,引入负序虚拟阻抗来降低系统阻抗及电压不平衡度,使系统微源容量合理分配。文献[11]采取分层控制策略对系统PCC 节点电压进行不平衡度调节。文献[12]在下垂控制基础上,调节下垂控制系数,降低了微电网运行成本,并使其运行更加可靠。文献[13]基于拉格朗日乘子法实现微电网最优化可靠运行。文献[14-15]采取虚拟一致性变量法让微网系统运行更加可靠,可应对微网系统的拓扑变动,但其精度易受系统通信影响。文献[16]将分布式次梯度算法与一致性算法相结合,以频率偏差替代功率偏差,运用该算法求解模型实现微网系统最优运行,但其控制方法太复杂。
本文主要研究微网系统的运行控制,并采取基于一致性算法的分层控制策略保证系统安全可靠稳定运行。第一层采取下垂控制,引入虚拟阻抗并对电压、电流环参数进行设计;第二层采取分布式一致性算法解决上层控制导致的频率、电压偏差问题,让系统分布式微源容量合理分配。最后利用仿真算例来验证模型及控制策略的正确性及合理性。
1 微网系统的控制方法
微网系统由分布式微源、储能装置、控制系统及负荷等组成,利用PCC 节点让其在离网、并网两种模式下自由切换。本文主要研究离网系统的控制策略,保证系统供电可靠性及运行安全性。
1.1 系统逆变器的控制方法
目前,系统逆变器的控制方法有以下几种,如PQ控制、U/f控制、下垂控制等。
(1)PQ控制:图1 是恒定功率控制原理图,若系统输出频率f∈(fmin,fmax),分布式微源在TPQ到SPQ点间运行,调整系统下垂曲线使分布式微源有功输出稳定在Pref处;若系统输出电压U∈(Umin,Umax),分布式微源在TPQ到SPQ点间运行,调整系统下垂曲线使分布式微源无功输出稳定在Qref处。此控制方法可保证系统有功功率和无功功率稳定、安全、可靠运行。
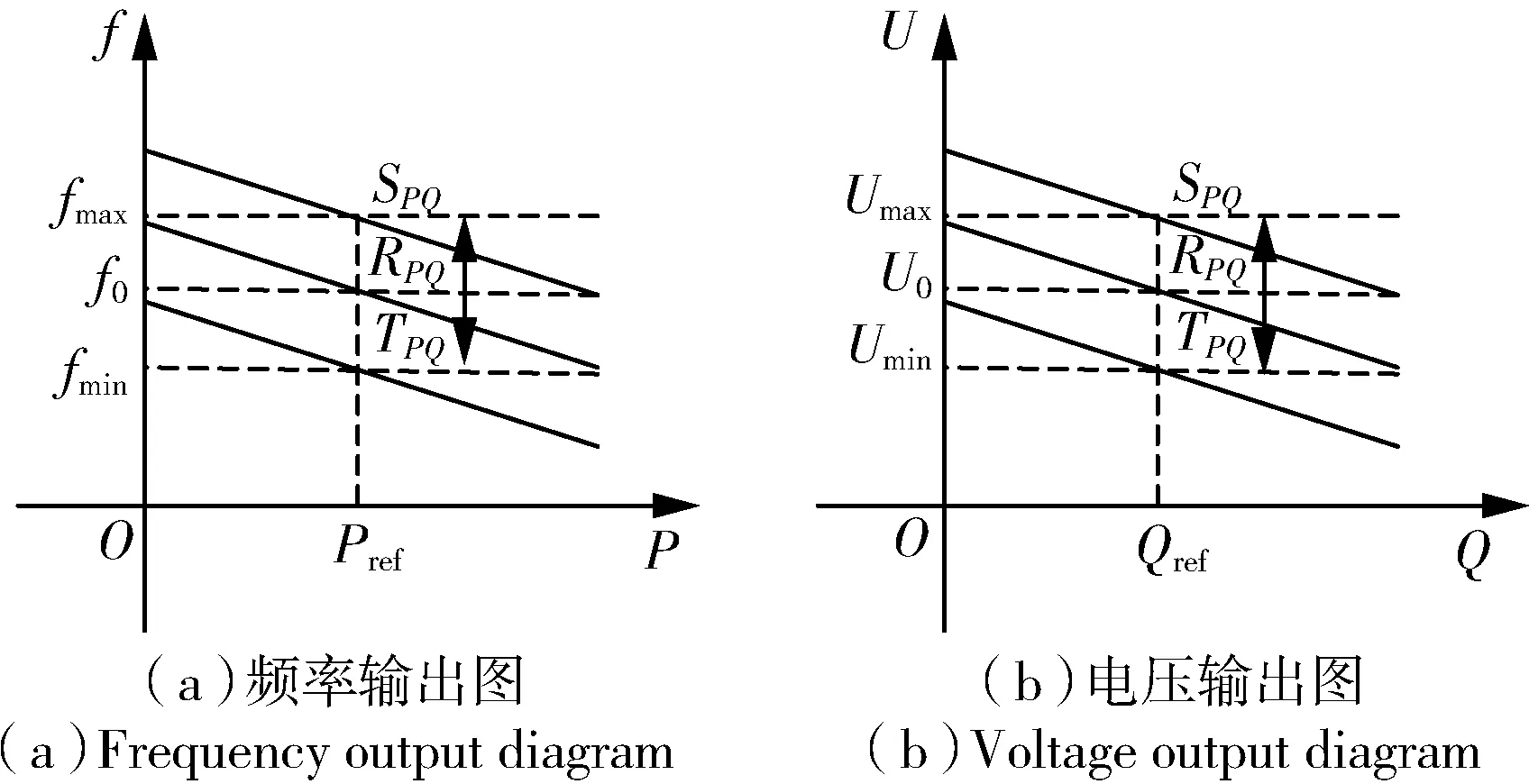
图1 PQ 控制原理图Fig.1 PQ control schematic diagram
(2)U/f控制:图2 是恒压恒频控制原理图,若系统输出有 功P∈(Pmin,Pmax),分布式微源在TU/f到SU/f点间运行,调整系统下垂曲线使分布式微源输出频率稳定在fref处;若 系 统 输 出 无 功Q∈(Qmin,Qmax),分 布 式 微 源 在TU/f到SU/f点间运行,调整系统下垂曲线使分布式微源输出电压稳定在Uref处。当分布式微源在TU/f到SU/f点间运行时,系统输出的频率、电压均维持稳定。

图2 U/f 控制原理图Fig.2 U/f control schematic diagram
(3)下垂控制:下垂控制与传统发电机下垂控制类似,调节下垂控制曲线控制系统分布式微源,使得频率与有功功率之间呈线性关系,电压与无功功率之间呈线性关系。通常逆变器输出电压与公共连接点电压的相位角差θ较小,则有sinθ≈θ、cosθ≈1,因此,图3 是其下垂特性曲线图。
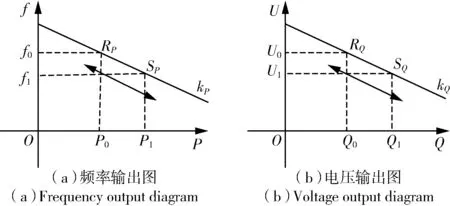
图3 下垂特性曲线图Fig.3 Sag characteristic curve
由图3 知,斜率kP、kQ为有功、无功功率下垂控制系数,表达式如下:
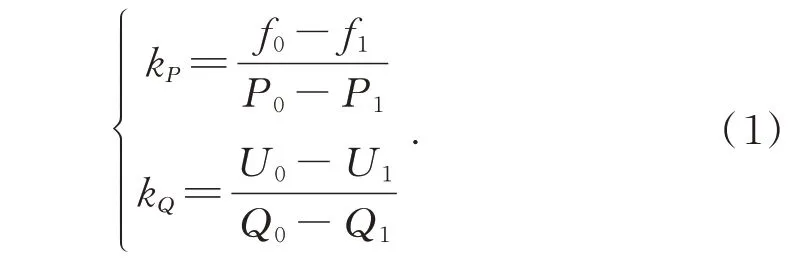
1.2 微电网系统控制方法
由于大电网供电可靠性差且供电成本偏高,分布式微源供电灵活且可靠性高,系统也可在离网及并网间自由切换。本文主要研究微电网离网系统的控制策略,分析系统在不同工况下宜采取的控制策略,以保持系统电压、频率稳定,功率精确分配。
目前微网系统采取的控制策略包括:主从控制、对等控制、分层控制,具体如下。
(1)主从控制:系统主从控制即选取主控微源,并将其余分布式微源作非主控微源。在离网工况下,主控微源采取U/f控制,以保证系统的频率、电压稳定;非主控微源采取PQ控制,以保证系统功率平衡,若系统主控微源异常,将严重影响系统的安全、可靠运行。
(2)对等控制:若系统采取对等控制,则微网系统中任意微源地位相同,且不区分主控微源或非主控微源。在并网工况下,系统采用PQ控制;在离网工况下,系统采用下垂控制。该方式不仅可直接控制任意微源,保证系统电压、频率稳定,而且在系统出现扰动时,也可采取相应控制策略保证系统电压、频率稳定,让系统安全、可靠运行。
(3)分层控制:综合考虑系统采取主从控制、对等控制后引起的不足,本文采用分层控制策略,图4 是系统分层控制结构原理图。第一层控制位于最底层,根据分布式微源特性采取相应控制策略,如PQ控制、Droop 控制;第二层控制解决上一层控制引起的电压、频率偏差,以及功率分配问题,并保证系统安全、可靠地运行。

图4 微电网分层控制结构图Fig.4 Hierarchical control structure of microgrid
综上分析,考虑系统常用控制策略,在微电网离网工况下为保证系统安全可靠运行,本文提出基于一致性算法的离网分层控制策略,解决系统频率、电压偏差问题,并在此基础上使系统分布式微源的容量得到合理分配。
2 基于一致性算法离网系统的分层控制
2.1 离网系统的初级控制设计
在初级控制层采取下垂控制,并通过低通滤波器得到系统瞬时有功功率、无功功率,其表达式如下:
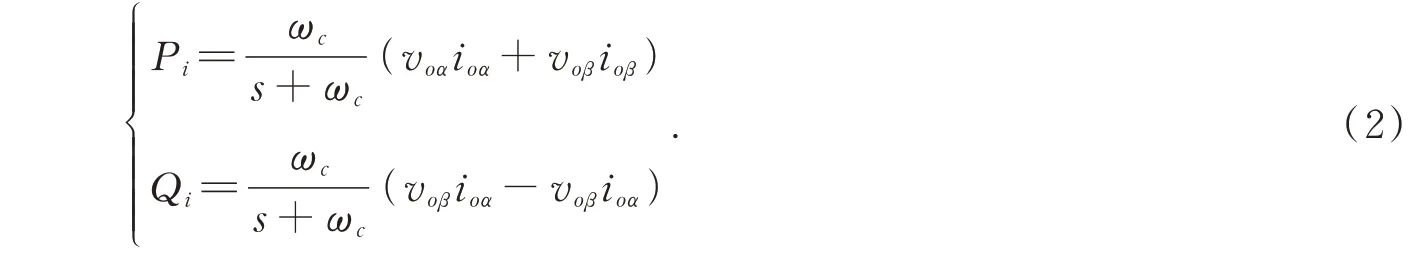
式中,voα、voβ和ioα、ioβ分别为αβ静止坐标系下的电压和电流;ωc为截止频率。化简后系统频率表达式如下:

式中,f*、E*分别为系统逆变器的参考频率和参考电压;f0、E0分别为系统逆变器的额定频率和额定电压;kP、kQ分别为系统逆变器的有功、无功下垂系数;Pi、Qi分别为系统逆变器的实际输出有功功率和无功功率。
2.1.1 基于αβ坐标系下虚拟阻抗设计
传统下垂控制线路阻抗呈感性且电感远大于电阻,但实际微网系统中电阻、电感数值相差不大。系统采取下垂控制策略会造成功率耦合,影响系统安全可靠运行。因此,可通过设计虚拟阻抗实现系统有功、无功功率解耦控制,虽会造成系统逆变器输出电压减小,但可提高系统的电能质量,图5 为虚拟阻抗环原理图。

图5 虚拟阻抗环原理图Fig.5 Schematic diagram of virtual impedance ring
式中,vvα、vvβ为αβ坐标虚拟阻抗的输出电压,i、i为αβ坐标的输出正序电流,Rv、Lv为虚拟电阻和电感。

系统加入虚拟阻抗后参考电压为U*ref(s),I(s)表示采集电流,Uref(s)表示下垂控制参考电压,Zv(s)表示虚拟阻抗,其数学表达式如下:

系统加入虚拟阻抗Zv(s)后,系统总阻抗呈感性,利用下垂控制对系统进行有功Pξ、无功Qξ解耦,图6 为系统功率解耦控制过程。
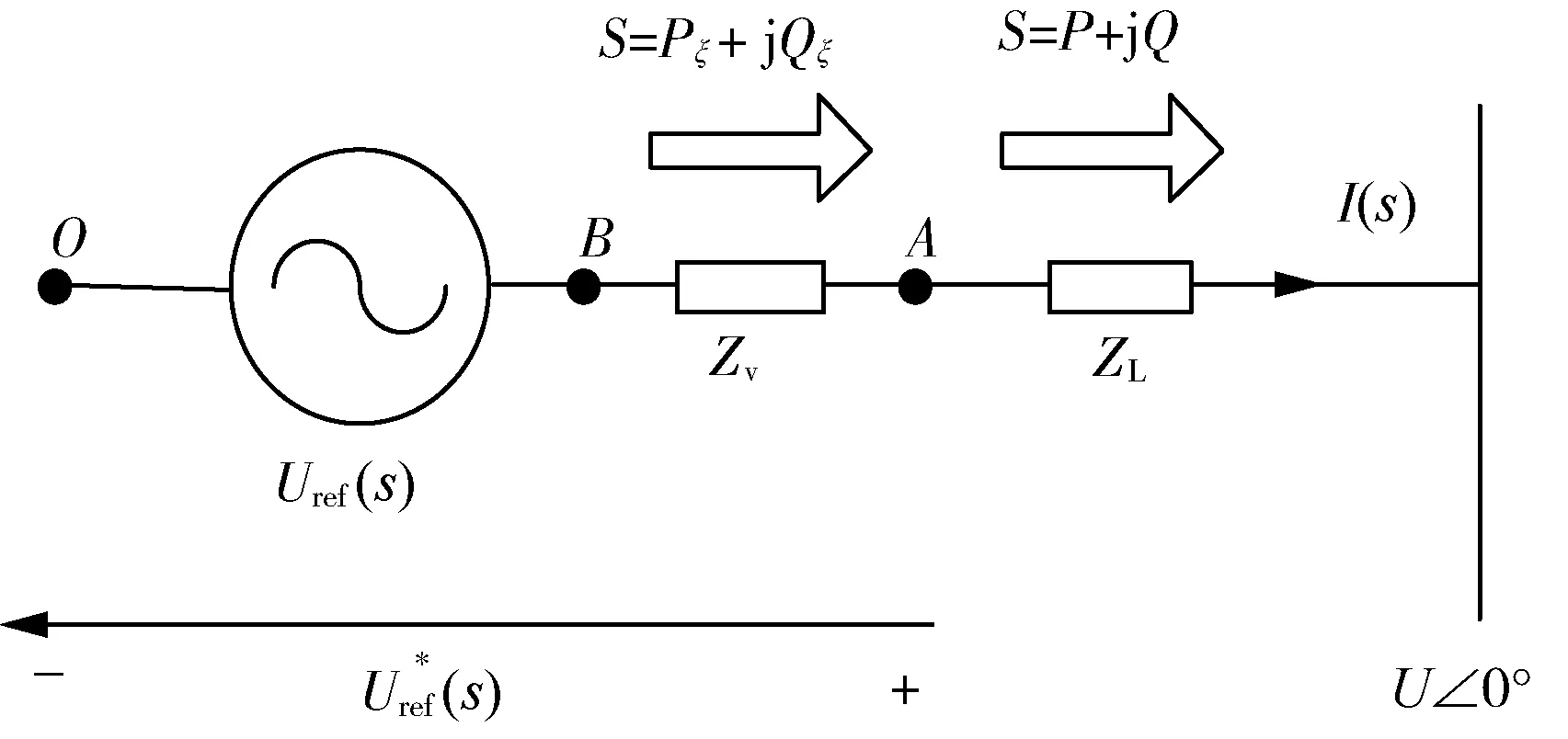
图6 系统功率解耦等效图Fig.6 Equivalent diagram of system power decoupling
有功功率解耦:微网系统引入虚拟阻抗后,即Zv=-Rv,如果Rv=RL,逆变器输出阻抗为感性,但虚拟阻抗无有功消耗,并在B点实现功率解耦,在A点有QA=QB,则:

式中,A点有功与B点虚拟阻抗角φξ有关,可利用虚拟阻抗角φξ来解耦控制A点有功功率。
无功功率解耦:微网系统引入虚拟阻抗后,即Zv=Xv,若(X+Xv)≫R,在A点有PA=PB。

式中,A点无功与B点虚拟电压E′有关,调节B点输出电压E′来解耦控制A点无功功率。因此,可在系统引入虚拟阻抗可实现其有功、无功解耦。
2.1.2 基于系统准PR 控制器的电压电流环设计
由于比例-积分(PI)控制器对交流信号控制动态性能相对差一些,且难以实现稳态无静差跟踪控制,其基波频率处幅值增益为零且存在相位延迟;而比例-谐振(PR)控制器抗干扰能力差,影响系统安全稳定运行。因此,系统设计了电压电流环控制器替代传统PI、PR 控制器,其传递函数为:

式中,kPV、kPI为电压、电流准比例谐振控制器的比例系数;krV、krI为谐振增益系数;ωcV、ωcI为电压、电流截止角频率。
由传递函数知,控制器性能由ωcV、kPV、krV决定。为设计合理的控制器,采用伯德图分析ωcV、kPV、krV三个参数对控制器的动态响应性能、控制系统带宽、系统基波频率幅值增益影响,获得的准PR 控制器的电压电流环设计参数如表1 所示。

表1 一次控制参数Tab.1 Primary control parameters
2.2 基于一致性算法的离网系统二次控制设计
当系统线路阻抗分布不均且系统并入不对称负荷时,离网系统初级控制策略的不足就显示出来了。如,系统线路阻抗不匹配时,下垂控制将导致系统电压偏差及频率偏差,严重时造成系统无功分配不均;系统不平衡负载接入时,导致PCC 节点电压质量下降及微源无功分配不均,影响系统安全稳定运行。
基于此,本文提出基于一致性算法的二次控制系统设计,在一致性算法下系统微源分布式控制器可以互相交换信息,以及获取全局电压、频率和无功的状态信息,也可将频率偏差反馈给本地控制并调整下垂系数消除系统频率偏差。利用相同原理对系统电压进行调整,消除电压偏差并合理调整系统无功及微源的容量分配。
2.2.1 二次控制调压调频原理
为保证控制系统稳定,本文初级控制采取下垂控制和PQ控制实现系统功率平衡,但也会造成相应频率、电压偏差,其原理如图7 所示。

图7 二次调频调压原理图Fig.7 Schematic diagram of secondary frequency modulation and voltage regulation
2.2.2 离网系统的二级控制架构设计
图8 是基于一致性算法的离网系统二次控制框架原理图,初级控制和二级控制组成本地控制,本文初级控制使用的是PQ控制及下垂控制,分布式二次控制器(DSCr)间进行信息交互并且和二级控制器组成分布式二级控制,产生下垂控制调节偏差量Δfi、ΔEi以及ΔQi。

图8 离网系统的二次控制框架图Fig.8 Secondary control frame diagram of off grid system
分布式控制器与邻居控制器进行功率、电压、电流等信息交换,然后通过一致性算法更新迭代直到收敛,并将收敛信息发送给本地二次控制。二次分布式控制器完成频率、电压、无功功率的调整。通过分布式二次控制产生的调节量分别为Δfi、ΔEi以及ΔQi,频率偏差叠加到对应的下垂控制的参考值之上,得到优化的参考值从而实现微电网的协调控制;电压偏差反馈参与无功功率调整,无功功率标幺值迭代收敛实现无功功率均分,同时无功功率偏差结合下垂控制消除电压偏差。
3 优化算法
3.1 基于系统的一致性算法
设变量xi为智能体i的状态量,如电压、电流等。若某网络达到一致时,该网络所有智能体状态值相等,表达式如下:

式中,n为智能体个数,第i个智能体的状态用xi表示,ui为一致性协议。若使所有智能体渐近收敛一致,一种典型一致性协议——连续时间一致性算法如下:

式中,aij为t时刻有向图G邻接矩阵Ak的第(i,j)项,一致性算法化简如下:

式中,x=[x1,x2,x3,…,xk]T表示信息状态,Lk(t)为图G的拉普拉斯矩阵,一致性算法化简如下:

式中,L为拉普拉斯矩阵。ρ为L谱半径,ρ=λ1(L)≥λ2(L)≥…≥λn(L)=0,λi(L)为矩阵L的特征值,λn-1(L)为网络代数连通度,其值越大表示系统节点路径越多,系统一致性收敛速度越快。
当系统信息值不连续时,其迭代过程是离散的,离散一致性算法如下式:

式中,D[k]∈Rn×n为系统状态转移矩阵,与上一时刻状态密切相关。
当整数i∈[1,n],平均值xiave收敛于全局一致值,其表达式如下:

若矩阵D[k]构造为双随机对称矩阵,则系统一致收敛于平均值,即:

可见,xiave的一致性收敛取决于系统初始值xi[0]。当系统收敛时,状态量迭代次数KN如下式:

3.2 离散一致性算法的流程图
实际系统采集信息类型是离散型,图9 是分布式控制器系统信息处理和一致性迭代的流程。

图9 分布式控制器实现过程Fig.9 Implementation process of distributed controller
理论上,各节点不断更新自身状态值到一个共同值来达到收敛,可能耗时较长;通过收敛精度γ来确定终止迭代及确认收敛的情况,收敛依据如下式:
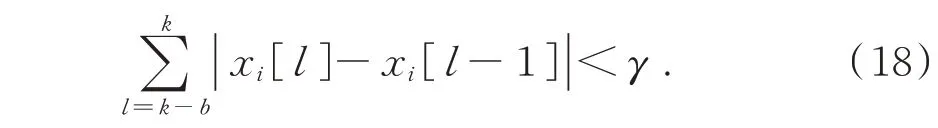
式中,γ为收敛精度,当取值较大时,收敛速度快;取值较小时,收敛速度慢。一般取10−2数量级,b是连续叠加的次数。
4 仿真研究
为验证系统分层控制策略对恢复频率、电压偏差,以及微源无功功率均匀分配的控制性能,进行算例仿真分析,设置逆变器直流侧由650 V 直流源供电,分布式微源容 量 比 为2∶2∶1;负 载1、2、3、4 为 平 衡 负 载,精 度γ=0.01,其他参数见表2 所示,图10 是逆变型离网模型。

表2 系统参数Tab.2 System parameters
如图10 所示的网络拓扑结构,其邻接矩阵A为:
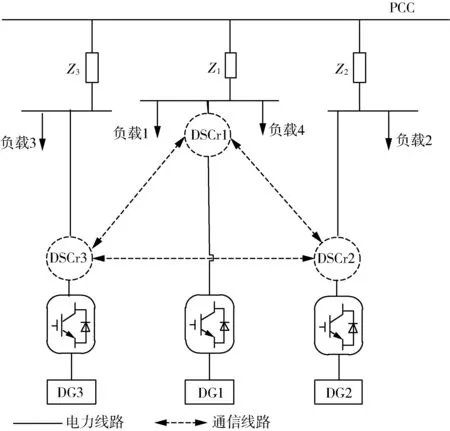
图10 系统结构图Fig.10 System structure diagram

因此,计算得到一致性迭代矩阵D为:

4.1 负荷突变分析
负载1、2、3 在0 s 时投入,在0.2 s 时系统采取分布式一致性控制策略,运行稳定后,在0.5 s 时投入负载4,得到仿真波形如图11 所示。
根据图11(a)无功功率标幺值知,在0.2 s 前系统下垂控制无功功率标幺值未收敛,即无功功率没有按照容量分配,图11(b)各节点平均电压与额定电压有较大差距,图11(c)各节点频率与额定频率也存在差距。在0.2 s~0.5 s 期间系统采取分布式一致性算法,二次控制器间信息相互交流,将平均值反馈给初次控制调整,此时系统无功标幺值收敛且无功功率按容量分配,图11(b)各节点平均电压稳定在额定电压处,图11(c)各节点频率稳定在额定频率处。在0.5 s 时系统负荷变化,无功功率标幺值通过局部信息进行短暂的调整仍然能收敛,无功功率按照容量分配,各节点平均电压、频率通过局部信息进行短暂调整后,在0.1 s 内达到稳定。根据图11(d)各节点电压一致性迭代过程可知,全局频率电压是DSCr 经过16 次迭代得到的收敛值,迭代16 次后即可满足给定精度γ,控制性能比较好。

图11 系统仿真波形Fig.11 System simulation waveform
4.2 迭代次数影响分析
由于收敛精度γ与迭代次数KN成反比,定义电压收敛偏差Δe如式(21)所示,并将其作为收敛指标。式中,EDi为分布式二次控制器(DSCr)得到的电压收敛值,EˉD为理论电压收敛值。
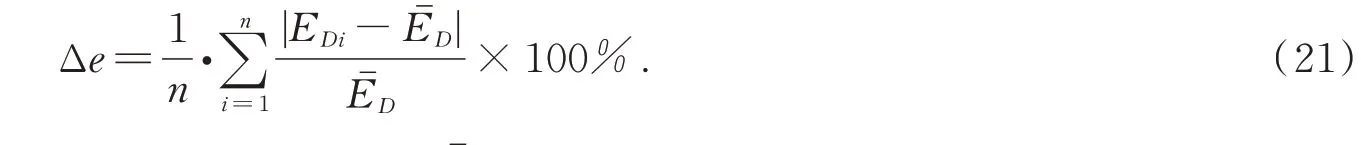
表3 是不同迭代次数时的电压收敛值,其中EDi表示第i个DSCr 的收敛电压;图12 是不同迭代次数下,系统无功功率、电压变化情况的仿真对比,以及各DSCr 得到的电压状态一致性迭代关系。

表3 不同迭代次数电压状态值比较Tab.3 Comparison of voltage state values with different iteration times
由图12 可知,随着迭代次数KN增大,系统稳态无功功率分配精度及收敛偏差相对更小,控制效果更好。系统采取一致性算法进行迭代时,系统控制器信息更新速度变快,暂态调节的超调量大、收敛耗时较长,但是其精度会更高,控制效果及控制实时性更好。

图12 不同迭代次数的仿真对比Fig.12 Simulation comparison of different iteration times
5 结论
本文采取基于一致性算法的微电网离网型分层控制策略时,虽然离网系统接入不平衡负荷造成PCC 节点电压不平衡度大,电压质量差,以及微源容量、无功分配不均,但采取该算法后不仅实现了系统有功、无功功率解耦,以及系统间电压、频率信息相互交流,还可以消除系统频率偏差,按微源容量合理配置系统无功,保证微电网离网系统的安全、可靠运行。最后通过算例仿真分析,验证了所提模型及分层控制策略的正确性与合理性。
