混合风电场接入含固定串补系统的次同步振荡特性分析
2022-06-09王俊茜翟文超
王俊茜,贾 祺,刘 侃,翟文超,王 健
(1.东北电力大学 现代电力系统仿真控制与绿色电能新技术教育部重点实验室,吉林 吉林 132012;2.国网辽宁电力科学研究院,辽宁 沈阳 110006)
0 引言
近年,由于风电的广泛接入,电力系统次同步振荡(Sub-SynchronousOscillation,SSO)事故频发[1]。2009年10月,美国德州某风电场双馈风电场(Doubly-Fed Induction Generator,DFIG)与串补电网间发生20Hz左右的次同步谐振事故,造成大量风电场撬棒电路损坏和异常脱网[2]。2012年12月,我国沽源地区风电场也出现了由串补电容导致风机6~8Hz振荡,严重地威胁了电网及风电场安全运行[3]。
国内外学者基于特征值分析、阻抗分析等方法,对DFIG风电场并网引发的SSO现象开展了研究,分析了DFIG风电场运行风速、串补度以及控制参数等因素对其振荡特性的影响规律。研究结果表明,DFIG风电场接入含固定串补系统发生的SSO现象是控制系统参与的感应发电机效应[4],[5]。振荡特性主要受运行风速、串补度及转子电流内环控制参数的影响,且随着DFIG风电场运行风速的增加、控制参数及串补度的减小,系统运行稳定性增加[6],[7]。但实际风电场通常包含直驱 风 电 场 (Direct-Drive Permanent Magnet SynchronousGenerator,PMSG)。文献[8]围绕沽源地区风电场次同步谐振现象展开研究,针对风电场控制参数固定的场景,基于阻抗分析法研究混合风电场中PMSG对次同步谐振的影响,结果表明,PMSG对系统次同步谐振存在影响,但并未分析风电场运行风速、控制参数等因素对振荡的影响演变规律。文献[9]基于特征值法进一步研究混合风电场SSO振荡特点,研究表明风电场中DFIG和PMSG风机比例、串补水平会对SSO产生影响,但未从机理上解释风电场接入影响系统稳定性的原因。
在PMSG风电场中,由于背靠背变流器的存在,使得永磁同步发电机与电网解耦。文献[10]基于时频分析方法,指出PMSG风电场不存在感应发电机效应。文献[11]以华北沽源系统的实际录波数据为基础,验证了PMSG风电场接入固定串补系统不会发生振荡;但新疆哈密地区发生PMSG风电场次同步振荡事故,须重新评估PMSG风电场的动态特性及影响因素。文献[12]通过电磁暂态仿真、阻抗模型等方法指出PMSG风电场的动态特性与变流器控制系统强相关,且不同控制参数下,PMSG对外呈现的容抗、感抗以及电阻特性可能不一致。此外,FACTS技术推动了SSO抑制方面的研究工作发展,目前已有的抑制SSO现象的方法多为在STATOM,SVC上增加附加励磁阻尼控制环节[13],[14]。
本文以PMSG,DFIG风电场并联接入含固定串补的系统为对象,研究了PMSG风电场对于DFIG风电场的SSO抑制作用。建立包含两种机型的混合风电场线性化模型,分析风机占比、控制参数、运行风速对系统运行性的影响。基于混合风电场动态阻抗模型进一步揭示系统次同步振荡机理。在EMTDC/PSCAD中搭建时域仿真模型,仿真结果验证了理论分析的正确性与可行性。
1 混合风电场建模
混合风电场拓扑结构如图1所示。DFIG风电场和PMSG风电场并联,经输电线路连接至电网,图中Lg,Cg分别为输电线路电感和串补电容。为了简化分析,假设风电场各台风机的运行状态是相同的,本文模型中的风电场采用单机倍乘的建模方式。
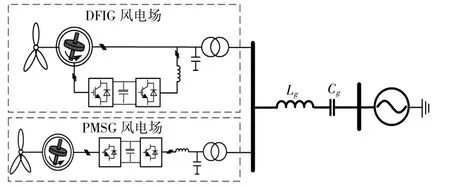
图1 混合风电场系统结构图Fig.1 Structure diagram of hybrid-based wind farm integration
1.1 DFIG风电场模型
DFIG拓扑结构及其控制系统如图2所示。
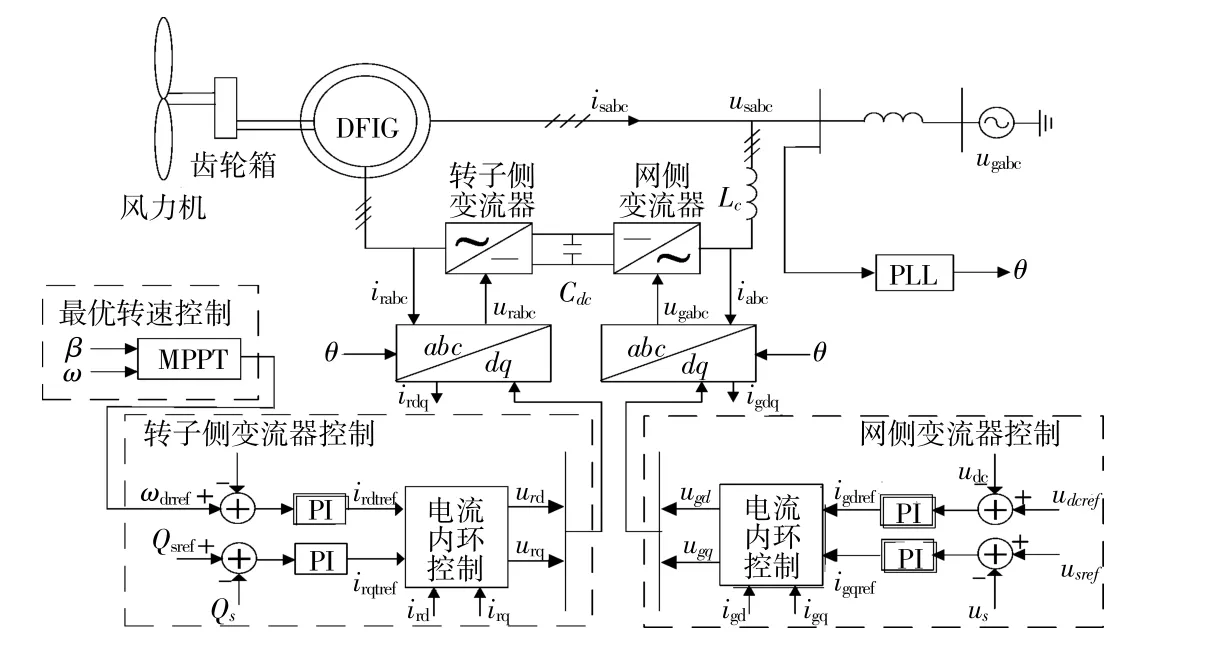
图2 DFIG风电场拓扑结构及控制策略图Fig.2 The topology and control system of DFIG based wind farm
DFIG主要由风力机、异步电机、转子变流器、网侧变流器4部分构成。转子变流器与网侧变流器通常采用电压矢量定向控制策略。为了实现风能的最大化利用,转子变流器通常采用MPPT控制策略;网侧变流器通常以直流电压与无功功率为控制目标。图中:ω,β分别为风机转速和桨距角;ωdr,ωdrref分别为转子转速及其参考值;Qs,Qsref分别为定子侧无功功率及其参考值;irdq,irdqref分别为dq坐标系转子侧变流器电流实际值及其参考值;irabc为abc坐标系转子侧变流器电流实际值;isdq,isabc为定子输出电流;urdq,urabc为转子侧变流器调制电压;usabc为abc坐标系下定子电压;us,usref分别为定子电压幅值及其参考值;udc,udcref分别为直流电容电压及其参考值;igdq,igdqref分别为dq坐标系下网侧变流器电流实际值及其参考值;igabc,ugabc分别为abc坐标系下网侧变流器电流实际值和调制电压;Cdc为直流电容;Lc为连接电抗;θ为锁相环输出相位。
在平衡点处线性化后,DFIG的数学模型为[15]
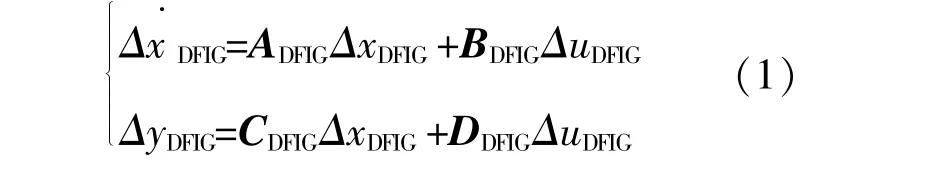
式中:ADFIG,BDFIG,CDFIG,DDFIG分别为DFIG风电场的状态矩阵、输入矩阵和输出矩阵。状态变量增量ΔxDFIG=[Δωdr,Δisd,Δisq,Δird,Δirq,Δigd,Δigq,Δudc,Δx1~Δx8],其中Δx1~Δx8为控制系统状态变量;ΔuDFIG=[Δusd,Δusq]T,ΔyDFIG=[Δisd,Δisq]T分别为输入、输出变量。
1.2 PMSG风电场模型
PMSG拓扑结构如图3所示。PMSG主要由风力机、永磁同步发电机、四象限变流器、滤波电路等构成。图中,机侧变流器采用定子电流ipsd=0的dq解耦控制策略,将永磁同步机转子角速度ωr与给角速度参考值ωrref比较,差值经PI环输出即为q轴电流参考值,dq轴电流经电流内环PI调节,形成变流器输出电压,经PWM调制,输出脉冲信号控制机侧变流器。网侧变流器采用电网电压矢量定向控制,将直流侧电压Udc与给定母线电压参考值Udcref比较,差值经PI环输出即为d轴电流参考值,dq轴电流经电流内环PI调节,形成变流器输出电压,经PWM调制,输出脉冲信号控制网侧变流器。

图3 PMSG风电场拓扑结构及控制策略图Fig.3 The topology and control system of PMSG based wind farm
图3中:v为风速;Lf,Cf分别为网侧变流器滤波电感及滤波电容;Lg为网侧电感;utabc为并网点电压实际值;ipsdq,ipsabc为定子绕组电流实际值;ipsdqref为定子绕组电流参考值;upsdq,upsabc为定子绕组电压;upgdq为网侧变流器输出调制电压;ipgdq,ipgdqref分别为网侧变流器输出电流实际值及其参考值;Udc,Udcref分别为直流电压实际值及其参考值;θr为转子侧输出相位;θPLL为锁相环输出相位。ωr,ωrref分别为永磁同步加转子转速及其参考值。
在平衡点处线性化后,得到PMSG的数学模型为[16]

式中:APMSG,BPMSG,CPMSG,DPMSG分别为PMSG风电场的状态矩阵、输入矩阵和输出矩阵。状态变量增量ΔxPMSG=[Δωr, Δipsd, Δipsq, Δipgd, Δipgq,ΔUdc,Δxp1~Δxp8];Δxp1~Δxp8为 控 制 系 统 状 态 变 量;ΔuPMSG=[Δupsd,Δupsq]T,ΔyPMSG=[Δipsd,Δipsq]T分别为输入、输出变量。
2 特征值分析
基于混合风电场线性化模型,分析风电场占比、PMSG风电场控制参数、运行风速等因素变化对系统振荡特性的影响。
2.1 风电场占比变化对系统稳定性的影响
DFIG风电场风速为4.5m/s,DFIG控制参数为(0.03,0.05);PMSG风电场风速为4m/s,PMSG直流电压环控制参数为(2,1000)、电流内环控制参数为(0.23,50);当PMSG风电场占比由0~50%变化(风机总并联台数为2 000台)、串补度由5%~30%变化时,DFIG和PMSG风电场并联接入含固定串补系统的次同步振荡模式变化轨迹如图4所示。
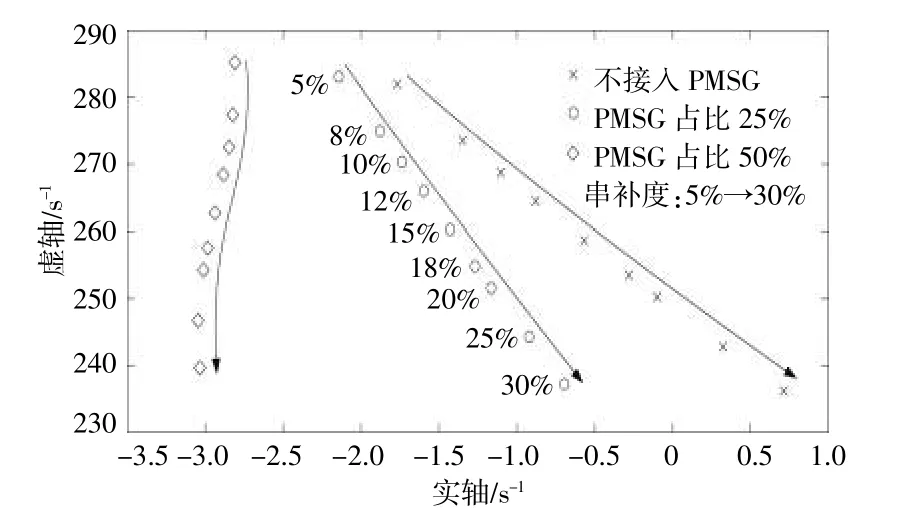
图4 定输送容量下次同步振荡模式变化轨迹Fig.4 The variation trajectory of SSOmode under fixed transmission capacity
由图4可知,随着串补度的增加,次同步振荡模式的阻尼逐渐减小,系统稳定性降低,且振荡频率逐渐减小;相同串补度下,随着PMSG占比的增加,系统稳定性增强。
2.2 PMSG风电场控制参数变化对系统稳定性的影响
DFIG风电场风速为4.5 m/s,并网台数为1 000台,DFIG控制参数为(0.03,0.05);PMSG风电场风速为4m/s,PMSG直流电压环控制参数(2,1 000),并网台数1 000台;当PMSG风电场电流内环控制参数在0.1~0.3变化、串补度在5%~30%变化时,DFIG和PMSG风电场并联接入含固定串补系统的次同步振荡模式变化轨迹,如图5所示。由图5可知,相同串补度下,随着PMSG风电场电流内环控制增加,次同步振荡模式的阻尼变化规律不明显。

图5 定控制参数下次同步振荡模式变化轨迹Fig.5 The variation trajectory of SSOmode under fixed control parameter
2.3 PMSG风电场运行风速对系统稳定性的影响
DFIG风电场风速为4.5 m/s,并网台数为1 000台,DFIG控制参数为(0.03,0.05);PMSG直流电压环控制参数(2,1 000)、电流内环控制参数(0.23,50),并网台数为1 000台;当PMSG风电场风速由4~6m/s变化、串补度由5%~30%变化时,DFIG和PMSG风电场并联接入含固定串补系统的次同步振荡模式变化轨迹如图6所示。
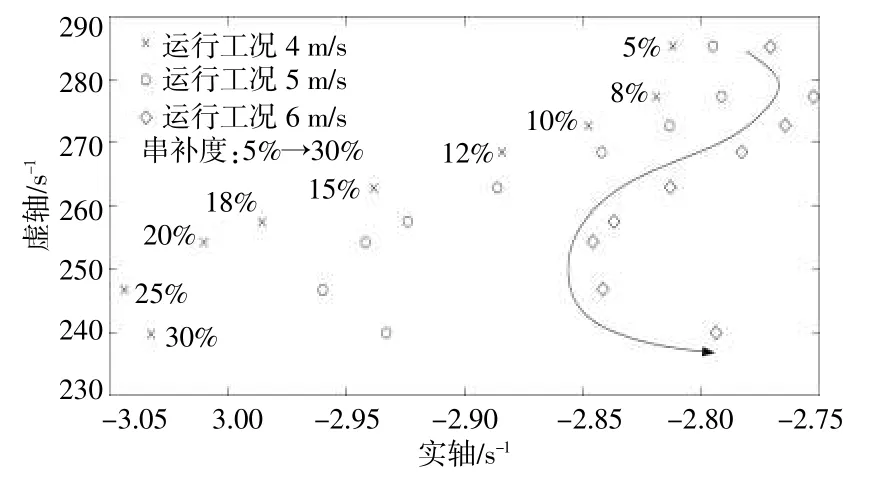
图6 定运行风速下次同步振荡模式变化轨迹Fig.6 The variation trajectory of SSOmode under fixed operating wind speed
由图6可知:随着串补度的增加,次同步振荡模式的阻尼呈现减小、增加、再减小的非线性变化趋势,且振荡频率逐渐减小;相同串补度下,随着PMSG风电场风速增加,系统稳定性降低。
3 PMSG风电场阻抗特性及对系统阻抗特性的影响
为进一步揭示混合风电场振荡机理,本文从风电场的动态阻抗特性角度开展研究,DFIG,PMSG风电场并联系统的动态阻抗(正序)表达式分别为

式中:ZPMSG为PMSG风电场阻抗;R1,X1分别为其等效电阻与等效电抗;ZDFIG为DFIG风电场阻抗;R2,X2分别为DFIG等效电阻与等效电抗;Ztotal为并联系统总阻抗。
由式(3),(4)可知,PMSG风电场阻抗和DFIG风电场阻抗,共同决定风电场并联系统总电阻的正负值;由于次同步频段下DFIG风电场负电阻特征凸显,系统总电阻Re(Ztotal)的第一项×R2和第四项R2×均<0,若想Re(Ztotal)>0,则须要选择PMSG风电场合适的控制参数、运行风速来保证R1>0;在满足上述条件下,R1取值偏小些,可能越有利于系统稳定。
本文利用频率扫描法,研究风电场占比、PMSG风电场控制参数、运行风速变化对DFIG次同步振荡特性的影响规律。具体扫频流程如下:①在稳定运行状态下的风电场端口注入一个频率连续变化的三相电压扰动信号;②测量风电场端口的输出电压Vmabc和输出电流iabc;③对输出电压和输出电流曲线进行傅立叶分解,基于Z(f)=Vm(f)/i(f),计算次同步频段下风电场动态阻抗。
3.1 风电场不同占比对次同步振荡特性的影响
DFIG风电场风速为4.5m/s,DFIG控制参数为(0.03,0.05);PMSG风电场风速为4m/s,PMSG直流电压环控制参数为(2,1 000)、电流内环控制参数为(0.23,50),当PMSG风电场占比为25%~50%时,PMSG风电场的动态阻抗如图7所示。
由图7可知:1~38 Hz频段内,PMSG风电场的动态电阻随频率增加而减小;38~40 Hz频段内,动态电阻随频率增加而增加;40~45 Hz频段内,动态电阻随频率增加而减小;1~39 Hz频段内,PMSG风电场的动态电抗随频率先增加后减小;39~41Hz频段内,动态电抗随频率增加而增加;41~45Hz频段内,动态电抗随频率增加而减小。考虑到DFIG风电场振荡场景中的振荡频率在2~20Hz(abc坐标系),随着PMSG风电场占比增加,PMSG风电场的动态电阻逐渐减小(以下分析中也重点关注2~20Hz风电场动态电阻特性)。

图7 不同占比下直驱风电场频率-阻抗特性Fig.7 The frequency-impedance characteristics of PMSG based wind farm under different proportions
保证风电场输送容量不变,DFIG风电场风速为4.5m/s、PMSG风电场运行条件如上所述,当PMSG风电场占比为25%~50%时,风电场并联系统的动态阻抗如图8所示。

图8 不同占比下系统频率-阻抗特性Fig.8 The frequency-impedance characteristics of the system under different proportions
由图8可知,2~20Hz频段内,风电场并联系统的动态电阻随PMSG风电场占比的增加而增大,有利于系统稳定运行。
3.2 不同控制参数对次同步振荡特性的影响
PMSG风电场风速为4 m/s、并网台数为1000台、直流电压环控制参数(2,1000),当电流内环控制参数由0.1~0.35变化时,PMSG风电场的动态阻抗如图9所示。

图9 不同控制参数下直驱风电场频率-阻抗特性Fig.9 The frequency-impedance characteristics of PMSG based wind farm under different control parameters
由图9可知:1~45Hz频段内,PMSG风电场的动态阻抗变化趋势与图5一致;随着PMSG风电场控制参数增加,PMSG风电场的动态电阻逐渐增加。
DFIG风速为4.5m/s、并网台数为1 000台、PMSG风电场运行条件如上所述,当PMSG风电场电流内环控制参数由0.1~0.35变化时,风电场并联系统的动态阻抗如图10所示。由图10可知:2~12Hz频段内,风电场并联系统的动态电阻随控制参数变化规律不明显;12~20 Hz频段内,风电场并联系统的动态电阻随控制参数增加而变大,该频段下控制参数增加有利于系统稳定。

图10 不同控制参数下系统频率-阻抗特性Fig.10 The frequency-impedance characteristics of the system under different control parameters
3.3 不同运行风速对次同步振荡特性的影响
PMSG风电场并网台数为1 000台、直流电压环控制参数为(2,1 000)、电流内环控制参数为(0.23,50),当风速由3.5~6m/s变化时,PMSG风电场的动态阻抗如图11所示。

图11 不同运行风速下直驱风电场频率-阻抗特性Fig.11 The frequency-impedance characteristics of PMSG based wind farm under differentoperating wind speeds
由图11可知:1~45Hz频段内,PMSG风电场的动态阻抗变化趋势与图5一致;随着PMSG风电场运行风速增加,PMSG风电场的动态电阻变化不显著。
DFIG风电场风速为4.5 m/s、并网台数为1 000台、PMSG风电场运行条件如上所述,当PMSG风电场运行风速由3.5~6m/s变化时,风电场并联系统的动态阻抗如图12所示。

图12 不同运行风速下系统频率-阻抗特性Fig.12 The frequency-impedance characteristics of the system under differentoperatingwind speeds
由图12可知,2~20Hz频段内,风电场并联系统的动态电阻随运行风速增加而减小,降低系统的运行稳定性。
4 仿真及结果分析
为验证上述分析的正确性,本节进行时域仿真分析,在EMTDC/PSCAD中搭建了图1所示的仿真模型。当串补度为25%、风电场输送容量恒定;DFIG风电场风速为4.5m/s、DFIG控制参数为(0.03,0.05);PMSG风电场风速为4m/s,PMSG直流电压环控制参数为(2,1 000)、电流内环控制参数为(0.23,50);t=6 s时投入串补电容,不同风电场占比条件下系统次同步振荡特性波形,如图13所示。

图13 不同占比下系统次同步振荡特性波形Fig.13 The SSO characteristic waveform of the system under different proportions
由图13可知,随着PMSG风电场占比的增加,系统稳定性增加,与理论分析结果一致。
当串补度为25%、DFIG风电场风速为4.5 m/s、并网台数为1 000台、DFIG控制参数为(0.03,0.05);PMSG风电场风速为4m/s、并网台数1 000台、直流电压环控制参数为(2,1 000);t=6 s时投入串补电容,不同PMSG风电场电流内环控制参数下系统次同步振荡特性波形如图14所示。

图14 不同控制参数下系统次同步振荡特性波形Fig.14 The SSO characteristic waveform of the system under different control parameters
由图14可知,随着PMSG风电场控制参数增加,系统稳定性增加,但变化规律不明显。
当串补度为25%、DFIG风电场风速为4.5 m/s、并网台数为1 000台、DFIG控制参数为(0.03,0.05);PMSG风电场并网台数1 000台、直流电压环控制参数为(2,1000)、电流内环控制参数为(0.23,50);t=6 s时投入串补电容,不同PMSG风电场运行风速下系统次同步振荡特性波形如图15所示。

图15 不同运行风速下系统次同步振荡特性波形Fig.15 The SSO characteristic waveform of the system under differentoperating wind speeds
由图15可知,随着PMSG风电场运行风速增加,系统稳定性降低,与理论分析结果一致。
5 结论
本文研究了在混合风电场接入固定串补系统中,PMSG对DFIG次同步振荡问题的影响作用。基于混合风电场线性化模型,对系统进行特征值分析,研究风电场占比、PMSG风电场控制参数、运行风速等因素变化对系统稳定性的影响。研究结果表明:①当PMSG风电场占比变化时(25%~50%),在2~20Hz频段内,PMSG风电场对外呈现正的阻抗特性,随着PMSG并网台数的增加,PMSG风电场的动态电阻减小,风电场并联系统动态电阻增加,系统运行稳定性增强;②当PMSG风电场电流内环控制参数变化时(0.1~0.35),在2~12Hz频段内,PMSG风电场对外呈现正的阻抗特性,风电场并联系统的动态电阻随控制参数变化规律不明显;12~20 Hz频段内,系统的动态电阻随控制参数增加而变大,有利于系统稳定;③当PMSG风电场运行风速变化时(3.5~6m/s),在2~20Hz频段内,PMSG风电场对外呈现正的阻抗特性,风电场并联系统的动态电阻随运行风速增加而减小,降低系统运行稳定性。
