风电机组故障的宽度学习诊断模型

郭宏宇,霍志红,许 昌,吾买尔·吐尔逊,周华建,程志明

（1.河海大学 能源与电气学院，江苏 南京 211100；2.新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐830052；3.河海大学 水利水电学院，江苏 南京 210098）

0 引言

作为一种清洁能源，风能已在世界范围内被广泛应用[1]。世界风能协会（WWEA）于2021年初公布的风力发电统计相关数据显示，2020年全球风力发电总装机容量已达744GW，其中我国以累计总装机容量290GW位居榜首[2]。

风电机组通常处于恶劣且复杂多变的工作环境，易受不稳定载荷等不可控因素的影响，这增加了风电机组发生故障的概率。故障诊断技术能帮助运行维护人员及时发现异常并做出相应的处理，从而延长风电机组的运行寿命。风电场监控与数据采集系统（SCADA）多被用来采集风电机组运行的关键参数，为风电机组状态运行分析与故障诊断提供可靠的数据支撑[3]。

在风电机组故障诊断领域的传统算法中，人工神经网络（ANN）是通过模仿人类大脑神经处理信息的方式搭建训练网络；支持向量机（SVM）是一种以统计学习理论为理论框架的机器学习算法；极限学习机（ELM）以单隐含层前馈神经网络为理论基础。TuerxunW[4]采用SSA对SVM的参数选取进行优化后，构建了SSA-SVM分类模型，提高了模型的故障分类准确率。

随着大数据、深度神经网络等新技术的出现，诞生了许多基于深度神经网络的风电机组故障诊断方法。王洪斌[5]利用深度置信网络（DBN）算法对风电机组主轴承状态进行分类，并有效提高了分类的准确率。吴定会[6]在卷积神经网络（CNN）算法的基础上，提出了风电机组轴承状态分辨模型，提高了模型的分辨精度，缩短了网络的训练时间。王超[7]提出了基于长短期记忆神经网络（LSTMNN）算法的风力机齿轮箱轴承故障诊断模型，用数据对模型进行验证，表明该模型明显提高了齿轮箱轴承故障的分类精度。

深度神经网络的深层结构模型复杂，涉及到大量的超参数，使得网络的迭代次数较多，网络训练缓慢，且易陷入局部最优解。深度神经网络为了获得更高的精度，不断叠加深层结构的层数，导致整个模型结构复杂且难以进行深层结构的理论分析。为了克服这些问题，文献[8]，[9]提出了宽度学习系统（BLS），它不仅结构简单、训练速度快、准确率高，而且还具有增量学习的优势[10]。本文在BLS算法的基础上，提出了一种基于BLS的风电机组故障诊断方法，并以风电机组故障数据作为试验数据进行分类诊断测试，分别比较了BP，SVM，ELM，DBN和BLS诊断模型的故障分类性能。

1 宽度学习故障诊断模型

1.1 BLS

BLS是基于随机向量函数连接神经网络提出的一种新型学习方法，在网络结构上与深度神经 网络有很大的不同，其结构如图1所示。

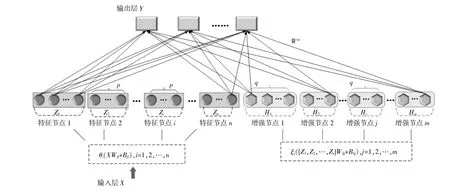
图1 BLS结构图Fig.1 Structure of BLSmodel

式中：X为输入层数据；Wfi，Bfi分别为随机权重和偏置，一般通过稀疏自动编码器进行微调产生最优值；θi为线性或非线性激活函数；Zi为含有p个神经元的第i组特征节点。

获得Zn之后，利用它可计算Hm。

式中：Hj为含有q个神经元的第j组增强节点；ξj为非线性激活函数；Whj，Bhj分别为随机权重和偏置。

通过进一步计算可以得到宽度学习模型。

式中：A为Zn和Hm联合构成的隐藏层矩阵；Wm为由A到输出层Y之间的权值。

在宽度学习系统网络中，Wfi，Bfi，Whj，Bhj等参数是随机产生的，并通过稀疏自动编码器进行微调，而且在训练过程中保持不变。在网络结构中，只有Wm是需要训练学习的。BLS的目标函数为

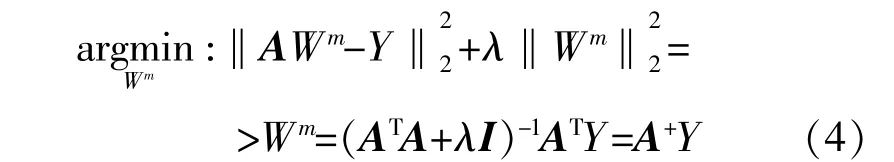
式中：λ为正则化系数；Y为输出量；AT为A的转置矩阵；I为单位矩阵；A+为A的伪逆矩阵。

‖A Wm-Y‖用于控制训练误差最小化，λ‖Wm‖用于防止模型过拟合。

Residue determination of dioxane in cosmetics by GC-QQQ-MS/MS with standard addition-internal standard correction method 4 24

1.2 宽度学习故障诊断模型

风电机组故障宽度学习诊断模型的计算步骤如下所示。

①导入SCADA数据：首先对原SCADA数据进行预处理，进行特征选择，归一化后导入到诊断模型中。

②训练集、测试集的划分：根据研究情况对导入的SCADA数据进行划分，导入数据的70%为训练集，30%为测试集。

③设置BLS网络的相关参数：主要包括特征点数量n、增强点数量m、某一个特征点Zi的p、某一个增强点Hj的q和λ。

④训练集Zn和Hm计算：利用式（1），（2）采用训练集作为输入量计算BLS的Zn和Hm。

⑤计算Wm和相关误差（‖Yˆ-Y‖2）：利用式（3），（4）计算BLS隐藏层到输出层之间的Wm和‖Yˆ-Y‖2。

⑥若误差满足要求则执行⑦，否则跳转执行③。

⑦测试集Zn和Hm计算：利用式（1），（2）采用测试集输入量计算BLS的Zn和Hm。

⑧故障分类计算：Ytest=HtestWm。

⑨输出结果：以图表形式输出故障分类结果并与实际结果进行对比。

计算流程如图2所示。

图2 宽度学习算法的计算流程图Fig.2 BLS flow chart

2 实例分析

2.1 SCADA数据预处理

本文采用内蒙古某风电场20160531-20170430连续365 d的SCADA数据作为故障分析样本数据。对这些数据进行消除、清洗、筛选等预处理后，选取风电机组的发电机过热（S1）、变流器冷却系统故障（S2）、励磁故障（S3）、馈电故障（S4）和正常（S5）5种状态作为分类诊断状态。每个状态选取200个样本，其中140个样本用于训练、60个样本用于测试，共选取700个训练样本，300个测试样本。在风电机组的5种状态下，用随机森林的袋外估计功能，对SCADA数据的特征量进行重要性排序后，最终提取环境温度、平均风速等27个具有代表性的特征量。样本归一化后的部分特征值如表1所示。

表1 风电机组5种状态下的样本特征值Table 1 Samples of five states characteristics of wind turbines

续表1

2.2 BLS相关参数设置

在BLS中，通过调整{n，p，m，q}和λ等参数可以提高模型精度。其中，{n，p，m，q}与BLS网络的结构有关，可随机选取，一般采用网格搜索法找到合适的取值范围；λ一般取很小的值。在{n，p，m，q}值不变的前提下，通过调整模型的λ，得到了BLS模型的故障分类准确率（图3）。由图3可知，当λ=2-30时，BLS模型的故障分辨精度最高。

图3 λ参数变化对模型分类准确率的影响Fig.3 Changes ofλand BLSmodel classification accuracy

在使用BLS模型时，{n，p，m，q}与λ的选取如下，n取值为100，m取值为600，p设定为20，q取80，λ的取值则是选用上述在模型调整过程中能达到模型故障分辨精度最高的值，即λ=2-30。

2.3 诊断模型性能比较

为了直观地体现BP，SVM，ELM，DBN和BLS模型的故障识别能力，分别绘制每一种诊断模型的混淆矩阵（图4）。混淆矩阵对角线元素表示能准确分类的样本个数，对角线元素数量越多，则模型的分类性能越好。非对角线元素表示错分类的样本个数，如果元素全为零，则是一个完美的分类器。

图4 5种诊断模型的混淆矩阵Fig.4 Confusionmatrices of the five diagnosticmodels

由图4可知：BP模型能够准确地分类S2和S5，但会把部分实际的S1预测为S3，实际的S3预测为S4，实际的S4预测为S2，在300个测试样本中，能准确分类269个；SVM模型能准确分类282个，对于S1和S3存在部分故障数据的类别判断错误；ELM模型能准确分类287个，同样对于S1和S3存在部分数据的判断错误，但判断错误的组数少于SVM，分类性能稍优；DBN模型对于S1和S3仍不能做到全部准确分类，但分类错误较少，能准确分类294个；BLS模型只有S3的两个样本错判为S4，在300个测试样本中，能准确分类298个，分类效果最好。

为了进一步评价模型的诊断性能，计算每一种模型的精度、召回率、F1值、准确率和算法运行时间（表2）。

表2 故障诊断模型的性能指标表Table 2 Performance indicators of fault diagnosticmodel

由表2可知：BLS模型的精度、召回率、F1值等性能指标均高于其它诊断模型，模型的分类性能较好，且由于宽度学习系统采用的是高效的增量学习，整个算法的运行时间远小于其他算法；BLS模型诊断准确率为99.33%，运行时间为0.329 s，能够较好地完成对风电机组故障的诊断。

3 总结

本文结合风电机组SCADA故障数据的时空相关性，提出了基于BLS的故障诊断模型。首先，对风电场SCADA数据进行预处理、特征选择后构成故障样本集；然后，采用BLS模型对这些故障样本进行分类。结果表明，该模型的分类准确率以及运行速度，均优于BP，SVM，ELM和DBN模型，最后在测试集上的分类准确率达到了99.33%，运行时间仅为0.329 s。