GDP 组合预测模型分析与研究

张春月 陈威 李诗 罗璐璐

（鞍山师范学院数学与信息科学学院，辽宁 鞍山 114007）

1 问题提出

GDP 预测是一个复杂的系统工程，通常会受到很多种因素的影响，同时各因素间还存在着错综复杂的影响关系，这为GDP 的预测增加了难度，无法保证预测的精度[3]。

2 基本原理

各种不同的定性或定量预测模型之间的关系并非有好坏之分，而是着手的角度不同，若加以结合，那么看待问题便会更加全面，取长补短，从而挖掘到更加具有代表性的信息，相应地最后的预测结果也会更加有信度和效度。换句话说，如果在预测时，发现某个单项预测方法得到误差较大的结果，便弃之不用，就可能使有用的信息从手中丢失，那当然会使预测精度受到影响。

在上面思想的推动之下，组合模型诞生了，它即是将多个模型的结果进行组合，以便充分利用各个模型的信息，从而有效提高预测精度。设有k 种方法，yit表示第i 种方法在第t 期的预测值，相关资料显示，存在以下两种计算第t 期组合预测值的方法：

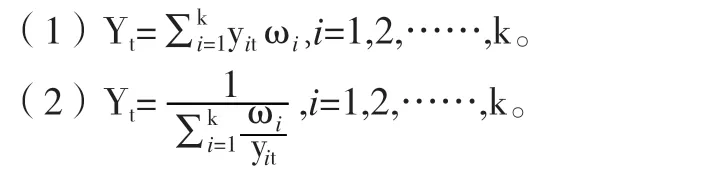
对于其中ωi的确定方法，常见的权重确定方法有六种，包括：等权重法、优势矩阵法、方差倒数法、残差倒数法、简单加权法、标准差法等[4]。

1.等权重法：即对每一种预测方法获得的权重是相同的，这种方法虽然简单易于操作，可是它的实用性却大打折扣，缺点在于它是对全部模型不分主次，平均对待，预测效果不理想。

2.优势矩阵法：假设两个模型对应的权重分别为ω1和ω2，次数n1和n2表示这两个模型比真实值有更好的预测效果。那么，这两个模型分别对应的权重不难算出。

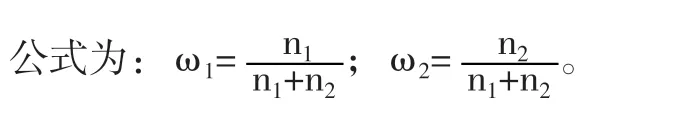
3.方差倒数法：通过误差平方和的大小来确定权重，即将高权重赋予误差平方和小的模型，另一种说法为预测误差平方和倒数法。预测精度经常用预测误差平方和进行度量，受到多种因素影响，通常来说单项预测模型的预测精度不尽相同。预测误差平方和越大导致该项预测模型的预测精度越低，毫无疑问，它在组合预测中的重要性就随之降低。这时，为了保证预测效果，就要在组合预测模型的组合预测中赋予较大的加权系数。

黑水虻幼虫在水产饲料方面也有较多的应用研究。胡俊茹等采用等氮等脂方法，将黑水虻幼虫粉按照不同的比例替代黄颡鱼幼鱼日粮中的鱼粉，结果发现：当替代量小于30%时，黄颡鱼幼鱼增重量与对照组无显著差异，而且血清中谷丙转氨酶、谷草转氨酶、尿素和三酰甘油的含量均得到一定程度的降低。林启训等为了代替鱼粉，将黑水虻幼虫粉用于泥鳅饲料中，研究发现，当添加9%～11%的黑水虻幼虫粉，泥鳅的摄食状态和成活率与对照组相近[17]。

公式为：ωi=其中Qi即预测值与真实值之间差的平方和。

4.残差倒数法：与上述方法不同，当某单项预测模型的误差平方和越大的时候，相应地，它在组合预测中的加权系数就越小。

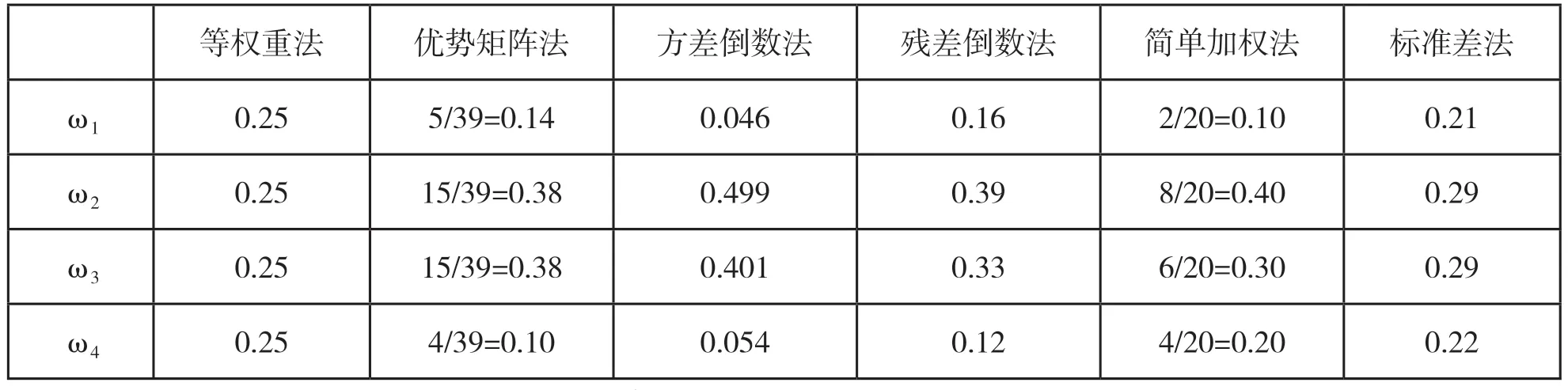
表1 几种权重确定法

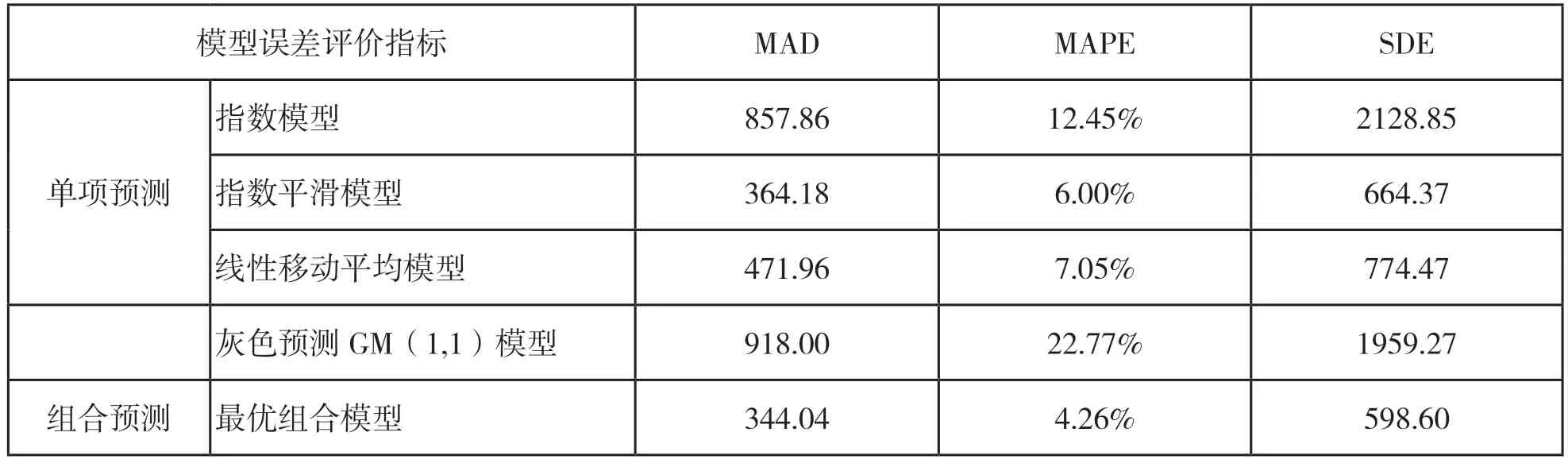
表2 几种模型误差比较

5.简单加权法：它是一种非等权平均方法之一。降序排序的对象是各单项预测模型预测误差的平方和，再根据各单项预测模型预测误差的平方和与权系数成反比的基本原理来安排权重，在组合预测中的加权系数越小意味着单项预测模型排序越靠前。

6.标准差法。

3 实证分析

用以上几种权重确定方法和模型组合方法，对指数曲线预测模型、二次曲线指数平滑法、线性二次移动平均模型、灰色GM（1，1）四个单项预测模型进行两种方法的组合预测，比较12 种组合模型，得出相对最优组合模型。

3.1 数据来源

数据来自国家统计局2020 年统计年鉴[5]，以1978-2016 年为训练集，2017-2019 年为测试集，旨在选择一种合适的模型预测2020-2022 年GDP 指标。

3.2 模型判断

3.2.1 图形识别法

借助R检验GDP序列平稳性与纯随机性，代码如下：

由GDP 时序图与相关图可得：GDP 序列的时序图有明显的递增趋势，自相关系数递减到零的速度相当缓慢，因此该序列是非平稳的。纯随机检验的结果显示，在各阶延迟下LB 检验统计量的P 值都非常小（<0.05），因此可判定该序列为非白噪声序列。

表3 测试集预测精度比较

3.2.2 差分法

对GDP 序列做二阶差分，对差分后的序列（GDP_diff）再次进行平稳性和纯随机性检验，代码如下：

由差分后GDP 时序图可得出，二阶差分后，GDP序列虽趋于平稳，但却为白噪声序列，即无法再提取有效信息，属随机游走序列，因此无法用ARIMA 模型对其进行建模。观察GDP 序列时序图，可观察出该序列不具有明显的季节成分，具有非线性趋势。

3.3 确定

采用指数曲线预测模型、二次曲线指数平滑法、线性二次移动平均模型、灰色GM（1，1）四种单一预测方法和组合预测模型，得到结果如下：

通过计算各种组合预测模型的误差指标值SDE（预测误差平方），MDE（绝对误差），MAPE（相对误差），比较得出最优组合预测模型，即权数为：ω1=0.046，ω2=0.499，ω3=0.401，ω4=0.054，运用i=1，2，……，k 的组合预测模型。

3.4 精度比较

通过以上模型各误差评价指标以及序列测试集精度的比较可知：组合预测模型的MAD、MAPE、SDE均相对最小，且在2017-2019 年测试集上预测精度均在90%以上，效果良好。因此可得出：单项模型的预测效果不及组合模型的预测效果，应采用组合预测模型进行预测。

3.5 预测

通过以上各模型比较，采用组合预测模型对2020-2022 年GDP 数据进行预测，结果为：2020 年为28198.70亿元，2021年为30514.33亿元，2022年为32976.53亿元。

4 总结

当下，国内经济形势发展已步入新常态阶段，GDP 增速整体是呈下行的发展趋势。那么如何精确分析GDP 增长呈现何种形式，如何准确判断十四五期间乃至未来十几年，经济走势是下行或是步入新的增长周期显得尤为重要。因此，本文提出GDP 新组合预测模型，旨在提升GDP的预测精度，为准确判断经济走势，为相关部门制定正确的经济发展战略和政策都有重要的现实意义。