随机丢包和信道约束的网络控制系统滤波
2022-06-08马运强王宗跃
马运强,王宗跃
(1.安徽机电职业技术学院 电气工程学院,安徽 芜湖 241000;2.淮海技师学院 机电工程系,江苏 宿迁 223800)
0 引言
随着工业技术日益复杂,传统控制系统难以满足当前大规模工业设备监控的需求,网络控制系统应运而生。20世纪末美国学者Walsh首次提出网络控制系统这一概念,网络控制系统(Networked Control Systems, NCS)是运用网络技术将空间分布的传感器、控制器和滤波器等连接而构筑的闭环控制系统[1~3]。相较于传统控制系统的点对点连接方式,NCS具有低成本、简化线路、资源共享等优点[4,5]。目前NCS逐渐成为现代控制科学研究的热点,它广泛应用于武器火控、航空航天和城市轨道交通等系统。然而,由于网络技术的介入,也会带来数据丢包、信道约束以及控制系统的稳定性降低等问题, 使得控制系统的分析愈加复杂[6]。因此,探究数据丢包和信道约束的网络控制系统具有重要的价值。
近年来随着5G网络技术的发展,网络控制系统的研究取得丰硕的科研成果。WANG[7]研究具有时延和丢包的控制系统,运用分布式伯努利模型描述丢包现象,基于连续时间Riccati方程推导出滤波器增益参数,构造了一类最优H2滤波器,但滤波算法不适用H∞滤波。TIAN等[8]针对网络控制系统存在信道约束和外部扰动问题,引入T-S模糊技术构筑非线性特征,推导出闭环系统稳定性的条件,但未考虑随机丢包对控制系统性能的影响。LIU等[9]利用随机伯努利序列建立不确定多数据包丢失的模型,研究一类不确定H∞滤波器的设计问题,基于随机理论和线性矩阵不等式技术给出滤波器存在的充分条件,但未分析信道约束带来的不利因素。李艳辉等[10]探究随机丢包的时滞离散网络切换系统H∞滤波问题,运用平均驻留时间法建立时滞模型,引用伯努利模型描述丢包过程,推导出滤波器与滤波误差系统稳定之间的关系。
上述文献单一研究网络控制系统数据丢包或信道约束问题,未能同时考虑数据丢包和信道约束对控制系统的影响,本文将在现有成果的基础上,研究同时存在随机丢包和信道约束的网络控制系统滤波器的设计问题,引入随机伯努利函数φ(k)刻画数据丢包过程,使用离散切换开关ϑ(k)描述网络信道约束状态,运用线性矩阵不等式技术探寻H∞滤波器存在的充分条件。
1 问题描述
针对传感器测量数据随机丢包和信道约束等问题,构建如图1描述的滤波控制系统传输模型。
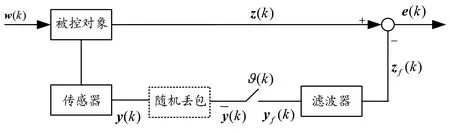
图1 系统传输模型
考虑如下网络控制系统:

(1)
其中,x(k)∈Rm,y(k)∈Rn,z(k)∈Rp分别为控制系统的状态数据向量、测量数据向量和待估计数据向量,w(k)∈l2[0,∞)为能量有界的外部扰动输入信号。A、B1、B2、C、和D为具有恰当维数的常值矩阵。
设计如下离散滤波器:
(2)
其中,xf(k)∈Rm,yf(k)∈Rn,zf(k)∈Rp分别为滤波器的状态数据向量、输入数据向量和输出数据向量,Af、Bf和Cf为滤波器的未确定矩阵。

(3)
使用离散切换开关ϑ(k)描述网络信道约束状态,根据网络信道连接是否成功,将信道约束的网络控制系统等价为两个独立事件。网络信道连接成功等效于切换开关闭合,标识事件1;网络信道连接失败等效于切换开关断开,标识事件2.
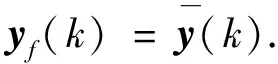
(4)

事件2 网络信道连接失败,滤波器接收的数据为前时刻数据,即yf(k)=yf(k-1).
(5)

结合式(4)和式(5),统一构建随机丢包和信道约束的滤波误差系统:
(6)
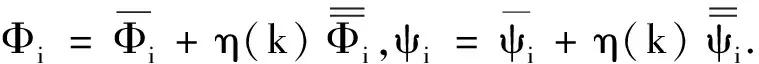
将事件1和事件2描述滤波误差系统等效为含有两个子系统的离散切换系统:
(7)

所探讨的目标是为网络控制系统设计如式(2)描述的离散滤波器,并满足下列条件:
1)在外部扰动信号w(k)=0时,滤波误差系统具有渐近稳定性。
2)在外部扰动信号w(k)∈l2[0,∞)和零初始状态时,对于任意给定的已知常数γ>0,若使得式(8)成立:

(8)
则滤波误差系统具有H∞性能指标。
2 滤波性能分析
定理1 考虑滤波误差系统,对于任意给定的已知常数γ>0,若存在恰当维数的正定矩阵P,使得式(9)成立:
(9)
则滤波误差系统具有渐近稳定性和H∞性能指标。
证明:取Lyapunov函数:
V(k)=XT(k)PX(k)
(10)
其中,P为正定矩阵。
Lyapunov函数的差分方程:
(11)

(12)
1)当外部扰动信号w(k)=0时,证明滤波误差系统具有渐近稳定性。
将w(k)=0代入式(12),得:
(13)
2)当外部干扰信号w(k)∈l2[0,∞)和零初始状态时,证明滤波误差系统具有H∞性能指标。
定义J(k)描述滤波误差系统的H∞性能指标,表达为:
(14)

由Schur补定理得不等式(9)保证了Ω<0,则:

(15)
将式(15)从0到∞累计求和,得:
(16)

3 滤波器设计
定理2 考虑滤波误差系统,对于任意给定的已知常数γ>0,若存在恰当维数的正定矩阵P和矩阵J、U、V和W,使得式(17)成立:
(17)
其中,
证明:考虑式(9)中的非线性项P-1运用MATLAB LMI无法求解,引入附加矩阵J:
(18)
考虑P>0,(J-P)TP-1(J-P)≥0,得-JTP-1J≤P-J-JT,代入式(18),得:
(19)
其中,
4 仿真示例
考虑如下参数的离散控制系统。
传感器测量数据传输成功率φ=0.8,方差α=0.4,H∞性能指标γ=1,取外部扰动输入信号
w(k)=2e-0.4ksin(0.4πk),运用定理2和LMI工具箱计算H∞滤波器参数矩阵
取系统的初始状态x(0)=[0.5 -0.5]T,滤波系统的初始状态xf(0)=[0 0]T.图2和图3分别为系统的状态真实值x1(k)/x2(k)与滤波器的状态估计值x1f(k)/x2f(k)的响应图,由图2和图3得,在外部扰动信号输入下,滤波器的状态估计值xf(k)较好地跟踪系统状态真实值x(k),降低扰动信号的干扰,滤波误差系统具有渐近稳定性。因此,针对随机丢包和信道约束的网络控制系统所提出的H∞滤波器是可行的。
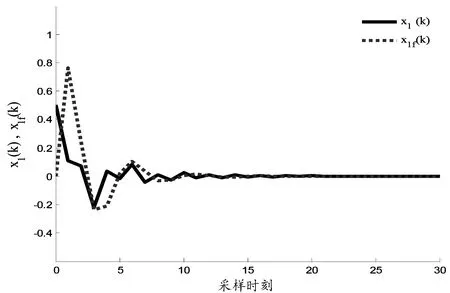
图2 真实值x1(k)与x1f(k)估计值

图3 真实值x2(k)与x2f(k)估计值
5 结论
本文研究随机丢包和信道约束的网络控制系统滤波器的设计问题,运用含有两个子系统的离散切换系统描述滤波误差系统,基于随机伯努利序列和离散切换系统证明滤波误差系统具有渐近稳定性并使得滤波误差系统性能指标小于给定值。仿真示例表明所提出的滤波器较好地跟踪系统状态,降低扰动信号的干扰。
