P-范分布尺度参数的Lq-似然比检验
2022-06-08胡宏昌
任 欢,胡宏昌
(湖北师范大学 数学与统计学院,湖北 黄石 435002)
0 引言
本文研究P-范分布尺度参数检验问题,其密度函数为
(1)
其中Γ(·)为伽马函数,λ=(Γ(3/p)/Γ(1/p))1/2,σ(σ>0)为尺度参数,μ为位置参数,p(p>0)为形状参数(定义参见文献[1~2])。
似然比检验方法是一种应用很广泛的检验方法,得到的深入结果很多,如:Chen和Liang[3]研究了带边界问题的伪似然比检验统计量的渐近形态,Schott[4]讨论了多元线性回归包络模型的似然比检验,Giudici等[5]研究了隐马尔可夫模型的似然比检验。Lq-似然比检验法是在似然比检验法基础上推广来的,近些年引起了越来越多的统计学家的关注,如:Huang等[6]用Lq-似然比方法对广义极值分布的形状参数进行了检验;Qin和Priebe[7]针对一般的污染分布提出了具有稳健性的Lq-似然比检验,得到了Lq-似然比检验统计量的渐近分布。然而,目前为止(据笔者所知)未出现用Lq-似然比检验方法对P-范分布参数进行检验。本文利用Lq-似然比检验法对P-范分布进行检验,并探讨统计量分布特点。
1 Lq-似然比检验
本节考虑P-范分布尺度参数假设检验问题。这里假定μ已知,不失一般性假定μ=0.设X=(X1,…,Xn)为取自总体P-范分布的一个样本,x=(x1,…,xn)是观测值序列(其中σp∈Θ⊂R是已知参数集合)。下面讨论假设检验问题:
H0∶σp∈Θ0↔H1∶σp∈Θ1
其中Θ0和Θ1分别为原假设和备择假设的参数空间。
P-范分布的Lq-似然函数为
(2)
则其Lq-似然比检验统计量为
(3)
其中C(σp,qn)为偏差纠正项,值为
(4)
2 主要结果
为得到本文主要结果,我们给出以下三个基本假设条件:
1){xt,t≥1}有界。
2)qn>0且当n→∞时,qn→1.
3)参数空间Θ是紧集且θ是Θ的一个内点。

(5)
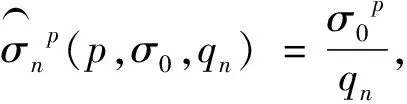
(6)
定理3 统计量Dqn(X)的分布密度函数为
(7)
其中
3 主要结果的证明
为证明本文主要结果,我们先给出引理1.
引理1[8]设Ψn是随机向量值函数,Ψ是θ的向量值函数,使得∀ε>0有
定理1的证明:由(2)式对σp求导得
(8)

(9)
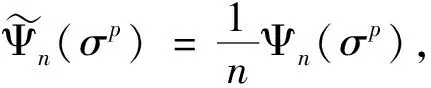

(10)
注意到
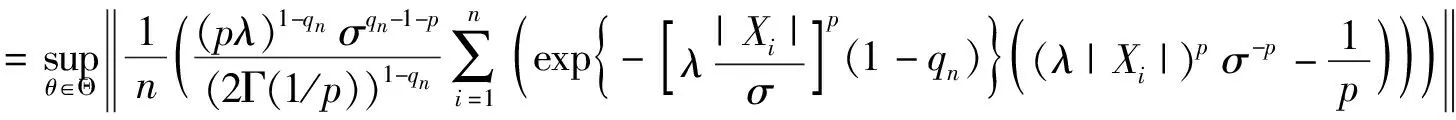
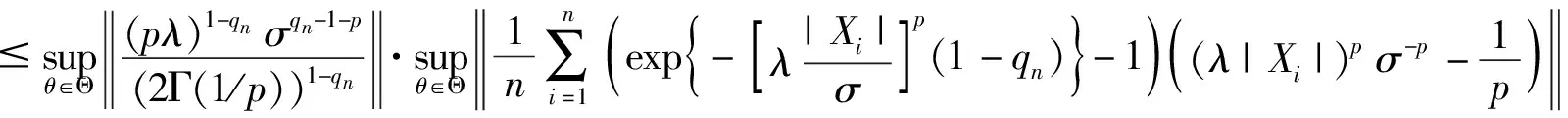

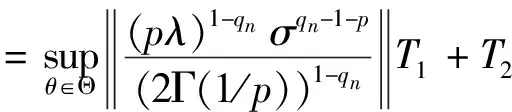
(11)
注意到
=T1(1)·T1(2)
(12)
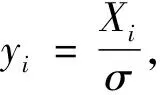
(13)
所以
(14)
则
(15)
即
(16)
又因为
(17)
则
(18)
即
(19)
由(16)式和(19)式可知,命题成立。
使得
(20)
则
(21)
因为
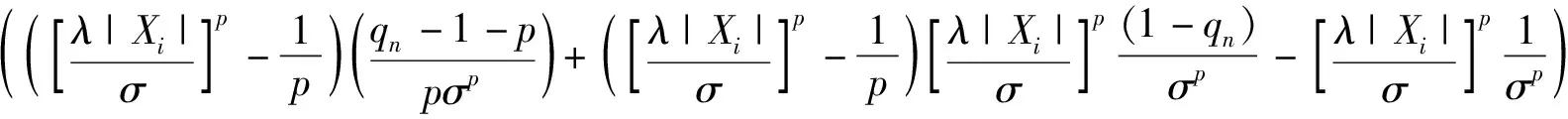
(22)

则
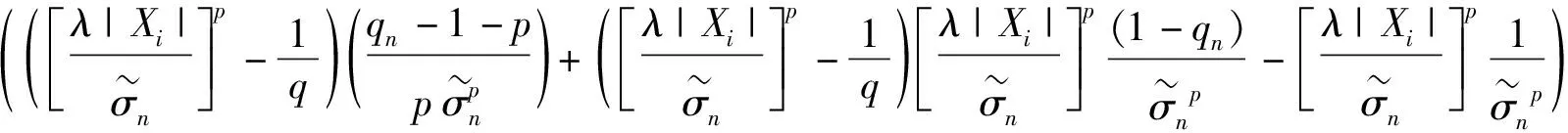
(23)
注意到

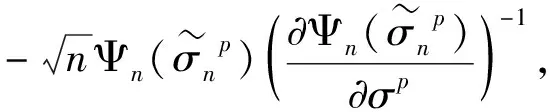
(24)
(25)
(26)
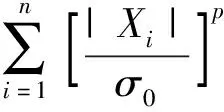
(27)

定理3的证明:设
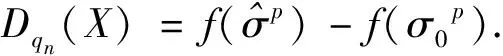
(28)

其中
4 模拟算例
本节将选取p为定值进行P-范分布的Lq-似然比检验,这里我们假设μ=0,α=0.05.令p=3,μ=0,σ=2,随机产生容量为100的样本。
1)检验:H0∶σ=2 ↔H1∶σ≠2.
由生成的样本以及公式5),我们可以得到统计量Dq(X)的值为
=-0.3886
由统计量的密度函数,我们可以得到
解得:q1=-1.0134,q2=0.8547
因为q1 2)检验:H0∶σ=3 ↔H1∶σ≠3. 同理可以得到统计量Dq(X)的值为 =20.8309 以及 解得:q1=-6.3578,q2=5.3708 因为Dq(X)>q2,所以拒绝H0. 通过上面的例子可以看出,检验结果均与模拟数据相符,从而也说明理论结果的可靠性。
