基于结构元的模糊值Caputo分数阶微分方程
2022-06-08郭元伟
亢 琳,郭元伟
(1.江苏师范大学科文学院基础部,江苏 徐州 221116;2.太原学院数学系,山西 太原 030032)
0 引言
众所周知, Hukuhara微分[1]是研究模糊微分的基本方法之一,在不确定或不完全动力系统中发挥了重要作用[2,3]。然而, 这种方法的缺点是模糊微分方程的解的支集会不断增大。为解决这一问题 Bede[4]于2005年提出了广义模糊微分、Stefanini[5]定义了广义Hukuhara差,都较好地解决了模糊数H差的存在性问题,在此基础上文献[6~7]较系统地解决了广义模糊微分方程解的存在性、唯一性等问题。模糊值分数阶微积分作为实值分数阶微积分的重要推广已取得较丰富的成果。Allahviranloo[8]给出了广义模糊值Caputo分数阶微分的定义,得到了与文献[6]类似的结果。Lupulescu[9]定义了区间值分数阶微积分,讨论了区间值Riemann-Liouville分数阶微积分、区间值Caputo分数阶微分的相关性质。Shen[10]利用Banach压缩映射原理研究了区间值Caputo分数阶微分方程解的存在唯一性问题。Ngo[11]利用逐步逼近法讨论了广义Lipschitz条件下Caputo型模糊泛函微分方程解的存在性、唯一性等问题,并给出具体的数值算法。郭嗣琮[12]于2004年提出了模糊结构元理论,虽然基于结构元的模糊数空间并不是完备的度量空间,但是这一理论给出的模糊数值函数有较好的解析式表达,所对应的模糊运算也相对简单[13]。基于以上考虑,本文首先给出了基于结构元的模糊值Riemann-Liouville分数阶积分的定义,讨论了其性质。其次,借助于广义模糊微分研究了模糊值Caputo分数阶微分,给出了其存在的充分条件,并讨论了模糊值Caputo分数阶微分和模糊值Riemann-Liouville分数阶积分之间的关系。最后,讨论了常系数一阶线性模糊值Caputo分数阶微分方程,并借助于实值Laplace变换给出了其解的具体形式。
1 定义及说明

数乘运算u+ν,ku分别定义为[3]:
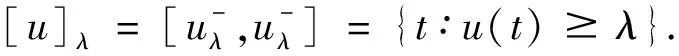
定义1[12~13]设A是有限模糊数, 若存在一个模糊结构元E和有限实数a∈,r∈+使得A=a+rE,则称A是模糊结构元E线性生成的模糊数。由结构元E线性生成的模糊数全体记作

下文中所讨论的模糊值函数均满足F(x)∈N(Ef).
定义2[15]设F(t)∈N(Ef). 若
或
成立,则称F(t)在t=t0处广义可微。特别地,若F(t)满足1)式,则称F(t)是gH1可微; 若F(t)满足2)式,则称F(t)是gH2可微。
引理1[15]设F(t)∈N(Ef),F(t)=f(t)+w(t)E, 其中f(t),w(t)是连续的实值函数。
1)若w(t)单调递增,则F(t)是gH1可微,且F′(t)=f′(t)+w′(t)E;
2)若w(t)单调递减,则F(t)是gH2可微,且F′(t)=f′(t)+(-1)w′(t)E.
2 基于结构元的模糊值Caputo分数阶微分
首先介绍实值Riemann-Liouville分数阶积分。若实值函数φ∈L[a,b],将φ的α∈[0,1]阶Riemann-Liouville分数阶积分定义为[14]:
与上述定义类似,下面给出模糊值Riemann-Liouville分数阶积分的定义:
定义3 对任意F(t)∈N(Ef),记F的α∈[0, 1]阶模糊值Riemann-Liouville分数阶积分为:
定理1 设F(t),G(t)∈N(Ef),且F(t)=f(t)+w(t)E,对任意a≤t≤b,α∈[0,1]有
证明 不失一般性,只证明1)式. 对任意a≤t≤b,α∈[0,1],由定义3可得
推论1 设F(t)∈N(Ef),F(t)=f(t)+w(t)E, 对任意a≤t≤b,α∈[0,1]有
例1 设F(t)=t+et·E,则由定理1可得
进一步有
现在介绍实值Caputo分数阶微分. 若实值函数φ∈L[a,b],将φ的α∈[0,1]阶Caputo分数阶微分定义为[14]:
与上述定义类似,下面给出模糊值Caputo分数阶微分的定义:
定义4 对任意F(t)∈N(Ef),记F的α∈[0,1]阶模糊值Caputo分数阶微分为:
简称gH-Caputo分数阶微分, 其中F′(t)表示广义可微. 特别地,若F′(t)表示gH1可微,则称之为gH1-Caputo分数阶微分;若F′(t)表示gH2可微,称之为gH2-Caputo分数阶微分.
定理2 设F(t)∈N(Ef),F(t)=f(t)+w(t)E, 则对任意a≤t≤b,α∈[0,1]有


证明 1)若w(t)单调递增,由引理1得F′(t)=f′(t)+w′(t)E,对任意a≤t≤b,α∈[0,1]有
2)若w(t)单调递增,由引理1得F′(t)=f′(t)+(-1)w′(t)E,对任意a≤t≤b,α∈[0,1]有
推论2 设F(t)∈N(Ef),F(t)=f(t)+w(t)E, 对任意a≤t≤b,α∈[0,1]有


定理3 设F(t),G(t)是由同一模糊结构元E生成的模糊值函数, 记F(t)=f(t)+w1(t)E,G(t)=g(t)+w2(t)E, 下列事实成立:


同理可得(F+G)(t)是gH1可微,且有
(F+G)′(t)=(f(t)+g(t))′+(w1(t)+w2(t))′E
=F′(t)+G′(t)
根据定理1可得
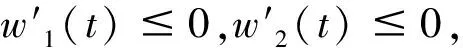
同理可得(F+G)(t)是gH2可微,且有
(F+G)′(t)=(f(t)+g(t))′+(-1)(w1(t)+w2(t))′E
=F′(t)+G′(t)
根据定理1可得


(F-G)′(t)=(f(t)-g(t))′+(w1(t)-w2(t))′E
=F′(t)-G′(t)
进而有
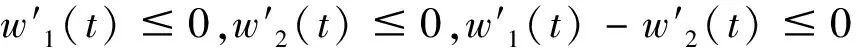
(F-G)′(t)=(f(t)-g(t))′+(-1)(w1(t)-w2(t))′E
=F′(t)-G′(t)
进而有
例2 设F(t)=t+et·E,则由定理1可得
进一步有
例3 1)设F(t)=t+t3·E,则由定理2可得
从而有

从而有
2)由定理3可得
定理4 设F(t)∈N(Ef),F(t)=f(t)+w(t)E,F(t)广义可微,对任意a≤t≤b,α∈[0,1],如下事实成立:


证明 不失一般性,只证1)式。若w(t)单调递增,由定理2可得
进而根据定理1有
=f(t)-f(a)+(w(t)-w(a))E
=F(t)-F(a)
定理5 设F(t)∈N(Ef),F(t)=f(t)+w(t)E,F(t)广义可微,则对任意a≤t≤b,α∈[0,1],如下事实成立:


证明 不失一般性,只证1)式.因为w(t)单调递增,由文献[9]中引理1知
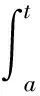
=f(t)+w(t)·E
=F(t)
3 模糊值Caputo分数阶微分方程
下面讨论常系数一阶线性模糊值Caputo分数阶微分方程,
(*)
其中Y(t)=y(t)+w(t)E,F(t)+f(t)+w0(t)E.
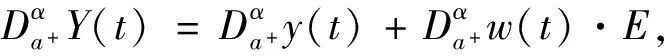
也即
从而可得
其中L[f(t)],L-1[f(t)]分别表示Laplace变换和Laplace逆变换。
定理6 设Y(t)=y(t)+w(t)E,其中y(t),w(t)是连续的实值函数,若w(t)单调递增,则Y(t)是gH1-Caputo可微,且Y(t)是(*)式的解,其中

也即
解得
定理7 设Y(t)=y(t)+w(t)E,其中y(t),w(t)是连续的实值函数,若w(t)非负且单调递减,则Y(t)是gH2-Caputo可微,且Y(t)是(*)式的解,其中
当m≤0时,(*)式解的讨论与上面类似,文中省略。
4 结论
本文首先给出了基于结构元的模糊值Riemann-Liouville分数阶积分的定义,讨论了其性质。其次,借助于广义模糊微分研究了模糊值Caputo分数阶微分,给出了其存在的充分条件,并讨论了模糊值Caputo分数阶微分和模糊值Riemann-Liouville分数阶积分之间的关系。最后,讨论了常系数一阶线性模糊值Caputo分数阶微分方程,并借助于实值Laplace变换给出了其解的具体形式。
