核心素养视角下师范生教学能力的因子分析

孙 茜，黄收友，刘群凤

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

0 引言

2014年教育部出台《关于全面深化课程改革落实立德树人根本任务的意见》，首次提出“核心素养体系”，明确要把“核心素养和学业质量要求落实到各学科教学中”。2020年9月4号的教育部新闻发布会上，国家发展改革委社会发司司长欧晓理也明确指出：要优化教师队伍结构，提升教师队伍能力，着力增强教师的核心素养。教师的教学能力为教师运用教科书、其他有关教学材料或采用某种特定方式从事教学活动，实现教学目标的能力[1]，教学能力决定着教师的整体任教能力。笔者根据从业几年的教育经验，发现现阶段师范生的教学能力不容乐观，具体表现为教学设计缺乏创新；教学过程满堂灌，教学重难点理不清；教学语言、板书不规范等，部分师范生不清楚什么是数学核心素养。关于如何提升师范生的教学能力，很多学者提出了自己的观点：文献[2]提出了通过拓展实践课程内容、注重个性差异等方法来提高师范生的教学能力；文献[3]提出了通过顶岗实习的方式来提高师范生的课堂教学能力等等。目前来看，利用统计思想方法，以数学核心素养为视角对师范生实践教学能力培养的探索较少。

1 相关概念介绍

1.1 因子分析法介绍[4]

因子分析是一种数据降维技术。它的基本思想是用少数几个新变量(因子)的线性组合来表示多个原变量之间的关系，且能尽可能多地反映原变量的信息。原变量是可观测的显在变量，而因子一般是不可观测的潜在变量。

1.2 因子分析法步骤[4]

1)数据预处理：将搜集到的数据进行正向化、标准化处理，记为X=(X1,X2,…,Xp)′;

2)判断变量是否可降维;

3)判别因子是否旋转;

4)确定因子个数m;

5)因子命名与正向化:命名与正向化后的因子仍记为F1,…,Fm;

6)给出样品的因子值：样品的m个因子值矩阵便代替了(正向化、标准化的)原始数据，成为样品的因子观测数据阵；

7)根据样品的因子值矩阵，可作因子分析的综合评价、因子回归、因子聚类等。

1.3 数学核心素养的概念内涵

核心素养目前没有精准的定义。对于核心素养的研究，不同学者表述各异：文献[5]认为“核心素养是指在一定时期内，帮助个人实现自我价值、成功生活与融入社会的最关键、最重要的知识、能力与态度的集合”。文献[6]认为“核心素养是学生在接受相应学段的教育过程中，逐步形成的适应个人终身发展和社会发展必要的必备品格和关键能力”。文献[7]认为“核心素养是指学生借助学校教育所形成的解决问题的素养与能力”。文献[6]认为在数学学科中，学科核心素养主要指数学学习者在学习数学或者某一个领域时应该达成的综合能力。现阶段《课程标准》中提到数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识这十个核心概念总体上反映了对学生数学素养的基本要求，是学生数学素养的重要标志。基于以上分析，为了适应学科发展需要，本文倾向于文献[8]的观点，将数学核心素养界定为“数学学习者在学习数学或者某一个领域时应该达成的综合能力”。高等院校的在校师范生只有自身具备这样的综合能力，才能在未来的教学中发挥出更大的能量。

2 数据收集与结果分析

2.1 数据收集

本文选取N大学的大一到大四的师范生进行教学能力问卷调查，问卷题目结合数学核心素养的培养要求以及师范生实践能力培养中的问题，综合课程设置、实践训练指导、职业认知、考核评价等因素。发放问卷350份，收回340份，其中有效问卷326份。将问卷结果统计后用SPSS软件对数据进行分析。分析结果如表1、2：

表1 可靠性统计量

从表1和表2可知，信度系数值为0.776，介于0.7～0.8之间，说明研究数据信度质量较好，分析因素被删除后的信度系数值并无明显提升，说明考虑的因素全部应该保留，进一步说明研究数据信度水平较好，可用于进一步分析。

表2 KMO 和 Bartlett 的检验

从表2可知，KMO为0.696，且显著性水平小于0.5，适合做因子分析。

因子解中每个变量被因子解释的方差估计量如表3，公因子方差都在0.5以上。

表3 公因子方差

表4中第一个因子的特征值最大，为3.747，前六个成分的特征值大于1，且累计方差解释率为66.345%.

表4 解释的总方差

从图1可看，从第7个因子开始，以后的曲线变得很平缓，因此可以抽取6个因子。

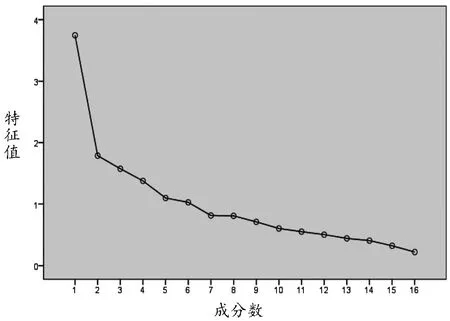
图1 碎石图

第一个因子z1受x1、x2、x3影响较大，命名为个人自身素质影响因子；第二个因子z1受x4、x5、x6、x7影响较大，命名为个人发展意识；第三个因子z3受x8、x9影响较大，命名为数学核心素养的影响因子；第四个因子z4受x10、x11影响较大，命名为年级影响因子；第五个因子z5受x12、x13、x14影响较大，命名为教学能力实训因子；第六个因子z6受x15、x16影响较大，命名为数学基础影响因子。

根据方差贡献率的百分比，得到教学能力得分模型

z=0.353z1+0.168z2+0.148z3+0.13z4+0.104z5+0.097z6

可知六个因子对个人的教学能力得分的影响按从大到小的顺序排列依次为：个人自身素质影响因子、主观影响因子、数学核心素养的影响因子、年级影响因子、教学能力实训因子、数学基础影响因子。如表5所示。

表5 旋转成份矩阵a

2.2 调查结果分析

1)个人自身素质特别是逻辑思维以及语言表达对个人的教学能力影响较大。这是因为个人的思维习惯、语言表达会影响教学的组织和呈现方式，其影响主要由环境、已接受的教育、生活习惯等所致。

2)个人的主观影响因子对教学能力的影响占比16.8%.主观影响因子受师范生在教学上是否有创新意识，是否做好师范生的职业发展规划影响较大。

3)数学核心素养对个人的教学能力得分影响也比较大，占比14.8%.

4)年级影响因子对教学能力的影响占比13%.一般认为，在校师范生所读的年级越高，接触的知识更广泛，学过的与教育教学能力相关的理论和实践课程比低年级要多。

5)相比其他因素，此次调查发现教学能力实训因子在对师范生的教学能力得分上仅占比10.4%，这与我们习惯上认为师范生“教学训练越多，教学能力提高越快”不一致，主要原因可能是由于部分师范生不重视教学实训，致使教学实训流于形式。从旋转成分矩阵可看出，此项因子受教学实践训练影响较大。

3 师范生教学能力提升建议

1)提升师范生的师范意识

高等院校应该在师范生进校时就引导他们提高自身的师范意识，以教师的专业素养和职业素养作为提升自己的目标，明确作为学生和准教师的双重身份，努力激发师范生的教育责任感，使师范生走上工作岗位后能够满足基础教育的要求。

2)提升师范生的自主学习能力、创新能力、教学实践能力。

高等院校应该加强制度建设，严格学生学业成绩管理、重修留级制度、考试违规处理等制度，在进行人才培养方案的设置时，第一学期尽量安排通识课程和专业导论课程，少安排专业课程，培养师范生的专业学习兴趣。同时在校园里多举办教师讲课创新大赛，粉笔比赛等赛事，提高奖励比例，刺激学生主动提高这些方面的能力。教师在学生的课程考核上应增加对师范生课程学习过程成绩的考核比重，降低课程卷面成绩的考核比重，并鼓励师范生对自己和准教师职业有信心，愿意制定目标主动学习。

3)以数学核心素养培养需求为导向，建立教师技能考核评价体系

提高师范生的核心素养能够提高教学能力。一是要让师范生了解什么是数学核心素养。可以通过课堂介绍、教学案例融入的方式让师范生切身体会这一内涵。二是制定与数学核心素养相关的教师职业技能训练评价标准。师范生只有将数学核心素养的培养融入到课堂实践中，理论与实践相结合，才能更好地了解核心素养的本质。

4)增加实训课程，完善教师职业技能训练机制

一是学校在师范生的每一个年级都应该增设师范类的理论课程和实践课程。特别是开设实践课程时，要求师范生必须认真学习解读课程标准和教材之后再备课。教案经过指导教师审核后才可以参加教学技能训练，训练后必须反思。二是组建专业的教师职业技能训练队伍，根据各类课程在训练中所承担的任务，将总目标分解并落实到具体责任人。三是可以邀请地方中小学的数学名师对师范生的教学基本技能进行指导，也可以聘请他们为师范生的兼职老师，通过反复教和练来保证训练效果。