盾构带压进舱开挖面稳定性分析及合理进舱换刀区间判断研究

胡威东， 周子扬， 封 坤， *， 邓朝辉， 刘议文

(1. 中铁第四勘察设计院集团有限公司， 湖北 武汉 430063； 2. 水下隧道技术国家地方联合工程研究中心， 湖北 武汉 430063； 3. 西南交通大学 交通隧道工程教育部重点实验室， 四川 成都 610031)

0 引言

近年来，盾构法在水下隧道与城市轨道交通建设中得到了广泛应用。当盾构在水下复杂地层施工时，刀盘刀具因被磨损而常需检修或更换，停机进舱作业在所难免。

当前，盾构施工换刀的方式往往根据地层条件选择： 1)在自稳能力较强的围岩环境中换刀时，一般采用常压直接开舱的方式。2)当处于软岩或富水地层时，一般会考虑3种方案： ①地层经过排水加固后在常压条件下敞开换刀；②从开挖面前方打竖井到刀盘前换刀；③利用压入空气稳定开挖面，工人在带压环境中进舱换刀[1-2]。带压进舱换刀由于适用范围较广，已在隧道工程中有了较多的应用。如： 程明亮等[3]通过北京地铁带压换刀施工实践，在最大工作气压0.28 MPa下成功带压动火焊接换刀；武汉长江隧道施工中首次在0.45 MPa高压下带压作业；南京扬子江隧道应用饱和气体带压换刀，在0.63 MPa气压条件下共进行240次换刀作业，更换刀具300余把[4-5]；南京地铁3号线穿越玄武湖区间隧道，成功采用水泥砂浆护壁技术在上软下硬地层保压换刀[6]；王住刚等[7]解决了西安地铁土压平衡盾构在富水密实性砂层中带压换刀的问题；段浩等[8]针对成都地铁1号线拟换刀位置进行分析，确定以富水砂卵石地层为主的换刀位置以及对应的换刀方案。

过高的气压环境会导致施工人员的有效工作时间降低，甚至损害工人健康，而过低的压力则会导致开挖面失稳。所以，因地制宜地选择带压换刀位置，并设置合理的气压是整个带压换刀施工的关键。针对开挖面稳定性判断，苏文德等[2]针对厦门轨道交通2号线跨海隧道，分别采用经验公式与改进楔形体模型的数值计算法计算最小带压进舱压力值，并对比实际测试气压大小，选取优化的计算方法；Taylor[9]在提出有限元强度折减法和超载法原理后，郑颖人等[10-11]、李欣[12]结合相关理论，采用数值计算方法解决了大量岩土工程问题，推动了极限平衡法在岩土工程等相关领域的应用；王林等[13]采用数值模拟与理论相结合的方法，揭示了隧道开挖面挤出破坏的局部失稳模式，并基于极限分析方法提出了一种考虑局部失稳模式的隧道开挖面挤出破坏新机制；宋洋等[14]通过模型试验与理论分析，建立了适用于砂-砾复合地层的盾构隧道开挖面极限支护力计算模型；张亚洲等[15]采用现场实测资料和数值模拟结果分析相结合的方法，探明扬州瘦西湖隧道泥水盾构在膨胀性黏土地层停机时开挖面失稳和地面塌陷的特性；吕玺琳等[16]基于村山氏极限平衡法和极限分析上限法，研究了盾构隧道开挖面稳定性，并推导出维持开挖面稳定的最小极限支护压力计算公式。

总的来看，现阶段对于盾构开舱换刀一般根据经验确定施工中的相关参数，并没有形成普适性的计算理论。对于地质复杂或破碎的地层无法准确判断气压平衡大小，导致开舱失败以至于不得不重新寻找合适的换刀位置，严重影响了施工进度；而对于合理换刀位置的判断，相关研究较少，无法在施工前预判适合带压换刀的区段。鉴于此，本文依托佛莞城际铁路狮子洋隧道工程，对水下不同地层条件进行开挖面稳定性计算分析，提出选取适合盾构带压换刀作业断面的判别方法，并针对依托工程给出合理换刀位置选择的建议。

1 开挖面稳定性计算分析

1.1 依托工程概况

佛莞城际铁路狮子洋隧道穿越地段地形为珠江两岸的平坦开阔地带，隧道全长6 150 m，盾构段长4 900 m。隧道上覆第四系土层，其中岸边段第四系土层以淤泥层和砂层为主，水下段以淤泥层、砂层及细圆砾土为主，下伏基岩以泥质砂岩、砂岩和泥岩为主。隧道穿越的地层主要为淤泥地层、砂层和圆砾土、W2中风化泥质砂岩以及W3强风化泥质砂岩。狮子洋隧道穿越地层纵断面图见图1。

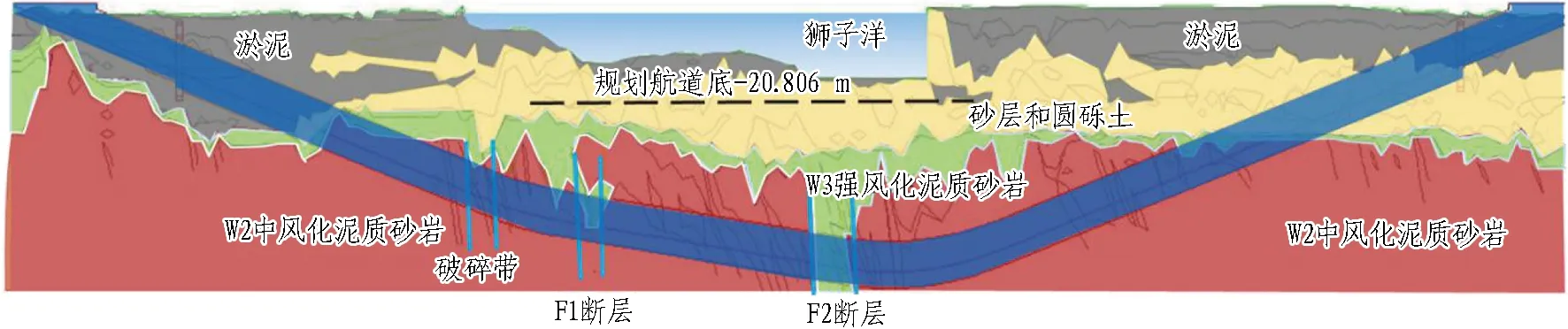
图1 狮子洋隧道穿越地层纵断面图

场区地表水主要为珠江狮子洋及两岸小河涌，工程所处区域雨量充沛，河网发育，为地下水的渗入补给提供了充足的水源，地下水位在1～5 m。

狮子洋隧道采用单洞双线布置，隧道内径12 m、外径13.1 m，标准环宽2.0 m，分块方式采用6+2+1，封顶块楔形量为30 mm。盾构采用“匠心号”泥水平衡盾构，盾壳0.14 m，衬砌结构采用C50高性能耐腐蚀混凝土，混凝土抗渗等级P12。衬砌结构示意图如图2所示。衬砌与盾壳计算参数见表1。

图2 衬砌结构示意图

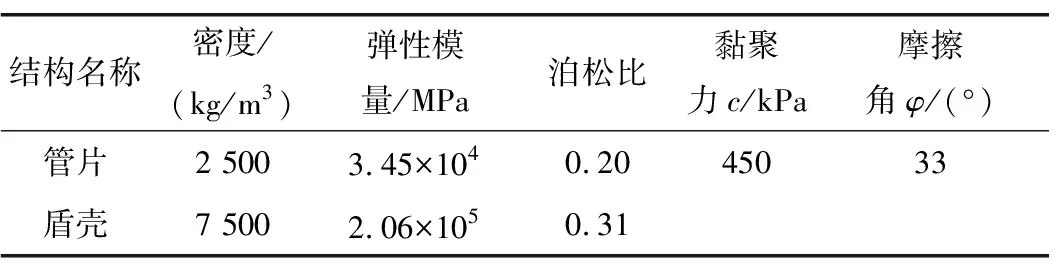
表1 衬砌与盾壳计算参数

1.2 数值模型建立

采用FLAC3D有限元软件进行建模，模型采用实体六面体单元，服从Mohr-Coulomb准则，对初始模型底面、左右边界及前后边界施加法向位移约束。

初始计算模型如图3所示。初始覆土高度为5 m，大致为盾构端头处的覆土高度，设置初始水压力，水位高度与模型上顶面齐平。围岩根据狮子洋隧道所穿越的W2中风化泥质砂岩、W3强风化泥质砂岩、圆砾土及淤泥4种不同地层环境分别设置。

设置初始计算模型后，开始设置隧道开挖步骤，保留8 m衬砌完成拼装模型，同时模型前端6 m保留盾壳结构，后端原盾壳部分用围岩材料回填填充(本计算不考虑注浆回填的影响)，此时停止隧道开挖，模拟盾构停机时的状态，如图4所示。

在停机模型的基础上，于模型上界面以面力的方式施加均布荷载，以模拟隧道埋深增大后上覆土层带来的影响，同时，在开挖面施加抵抗位移变形的面力。盾构带压工作环境为高压环境，超过一定界限将对人体机能产生不良影响，根据CJJ 217—2014《盾构法开仓及气压作业技术规范》[17]以及国外相关规范，带压进舱的气压大小一般不超过0.36 MPa[18]。在停机平衡计算时，设置0.36 MPa垂直开挖面向围岩内的表面荷载，模拟带压进舱最大气压条件。考虑到盾构刀盘的骨架支撑作用，盾构开口率设置为39%。据此，计算时在开挖面施加61%的纵向不平衡力反力。

图3 初始计算模型(单位: m)

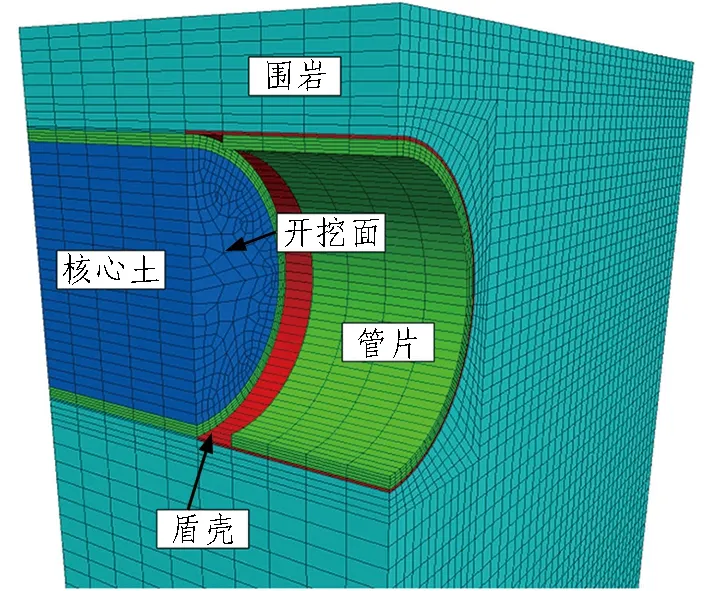
图4 停机模型

1.3 数值计算流程

结合有限元数值计算软件特征以及Mohr-Coulomb本构模型的特点，计算以模型不收敛或者位移增量突变时即判断开挖面失稳。计算流程如下：

1)设置模型围岩材料，施加开挖面荷载以及上表面荷载(初始为0)。

2)分别提取开挖面中间点(x=0，y=0)、上侧监测点(x=0，y=5)、右侧监测点(x=5，y=0)及下侧监测点(x=0，y=-5)处位移，计算每次位移变化斜率Ki。测点位置示意图如图5(a)所示。

3)肖明清[19]提出的数值计算中可作为极限状态的判断条件如下： ①有限元计算迭代求解不收敛[20];②有限元计算位移出现突变[20];③超过极限剪应变的围岩深度达到一定范围;④受拉破坏区深度超过一定范围。本文将计算出现不收敛情况以及开挖面位移突变视为达到极限平衡(当4个监测点中斜率增长λi=Ki+1/Ki大于2时,认为此时位移增长迅速，视为位移突变[14]，见图5(b))。

(a) 测点位置示意图

Δx为上覆荷载增量; Δyi为第i区间内位移增量; Δyi+1为第i+1区间内位移增量; Ki为第i位置斜率; Ki+1为第i+1位置斜率。

4)根据位移变化斜率及计算收敛情况判断开挖面是否失稳。若开挖面处于平衡状态，增大上覆荷载重复第2)步骤计算；若开挖面失稳，则此时上覆荷载大小即为失稳临界荷载。

5)对隧道区段采用全土柱理论计算隧道上部大致上覆荷载，对比对应地层临界荷载大小，判断是否适合带压换刀。

数值计算流程图如图6所示。

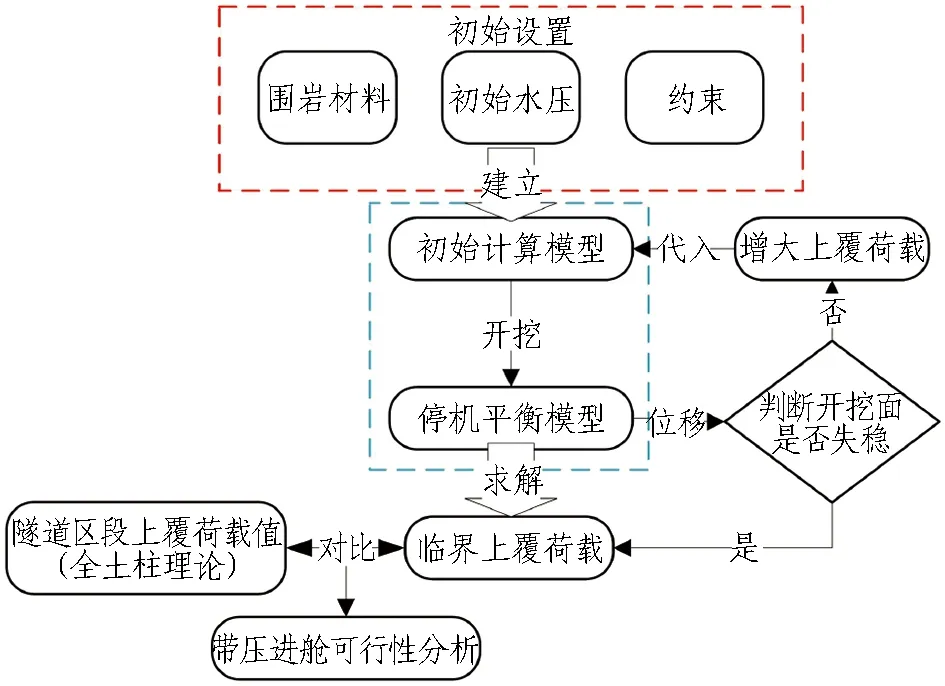
图6 数值计算流程图

按照上述计算方法，为探究不同地层围岩环境对带压开舱施工的影响，选取狮子洋隧道施工过程中洞身穿越的4种典型围岩进行试算，计算时按照如表2所示的土体性质参数取值，得到不同围岩环境下逐级增大上覆荷载时开挖面位移变化情况。

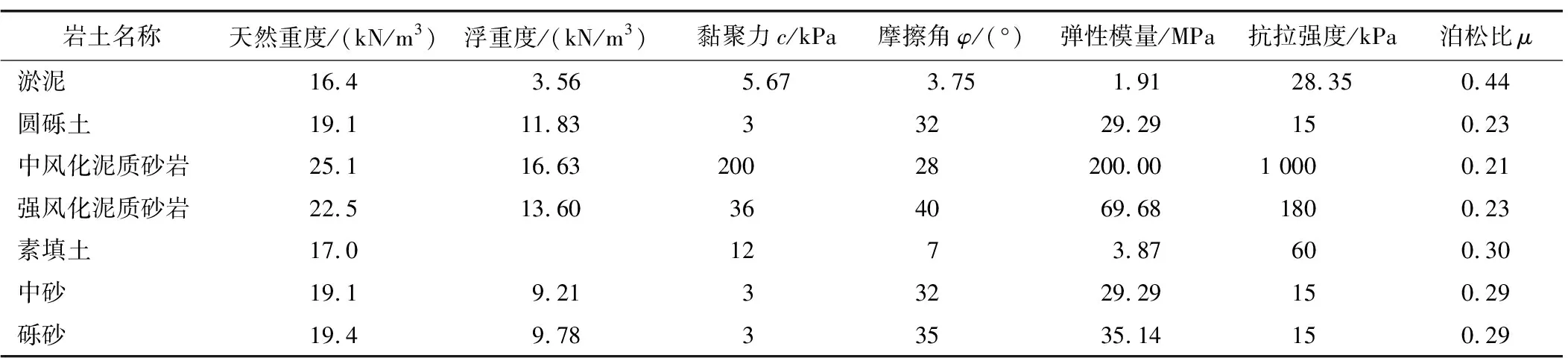
表2 狮子洋隧道土体性质参数

1.4 数值计算结果分析

1.4.1 圆砾土地层

圆砾土地层开挖面位移与上覆荷载关系如图7所示。在围岩环境为圆砾土地层时，当上覆荷载较小，开挖面上部位移有向内挤压的趋势，开挖面下部向外挤出。当上覆荷载持续增大至0.3 MPa时，λi的值为5.60，可以判断此时开挖面发生失稳。在上覆荷载作用下，开挖面位移较大，下部监测点最大位移接近45 mm。当上覆荷载持续增大至0.45 MPa后，计算已无法正常收敛，后续计算失效。

1.4.2 中风化泥质砂岩地层

中风化泥质砂岩地层开挖面位移与上覆荷载关系如图8所示。中风化泥质砂岩地层岩性较好，上覆荷载较小时开挖面位移稳定，在开挖面荷载推动下，开挖面向内轻微变形；当上覆荷载超过0.3 MPa时，开挖面有向外挤出变形的趋势，且随着上覆荷载的持续增大，当上覆荷载增大到0.9 MPa时，最大挤出位移达到1.48 mm，λi的值为2.28，可以判断在此荷载作用下开挖面发生失稳。

1.4.3 强风化泥质砂岩地层

强风化泥质砂岩地层开挖面位移与上覆荷载关系如图9所示。当上覆荷载较小时，开挖面产生较大的向内挤压变形，在实际施工中可采取减小舱压或者采用常压换刀的方式，避免浅埋时带压换刀风险。当压力增加到0.56 MPa时，λi的值为2.804，此时发生位移突变，开挖面失稳。

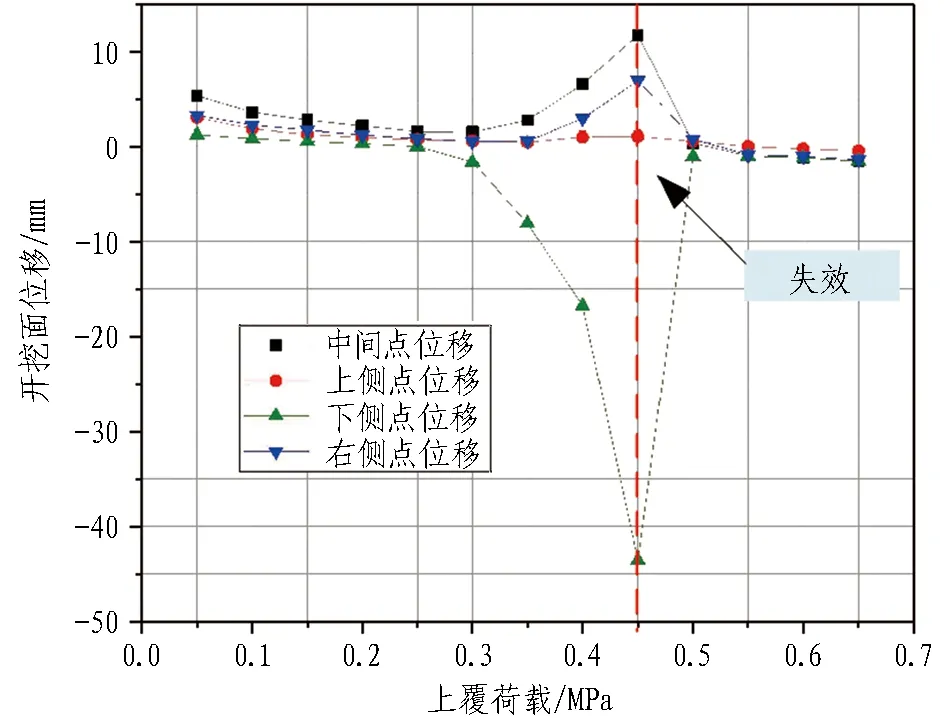
图7 圆砾土地层开挖面位移与上覆荷载关系

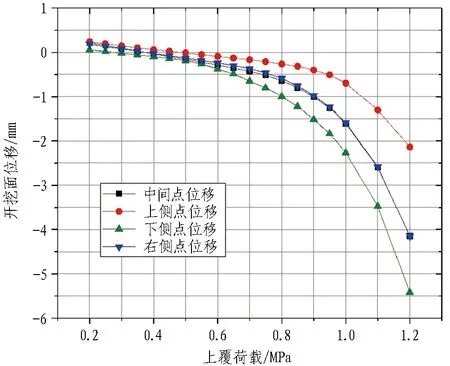
图8 中风化泥质砂岩地层开挖面位移与上覆荷载关系

图9 强风化泥质砂岩地层开挖面位移与上覆荷载关系

1.4.4 淤泥地层

对于淤泥地层，在不施加上覆荷载的条件下，开挖面位移随着计算步的增加而持续增大，数值计算无法收敛。开挖面上端受垂直开挖面荷载的影响向内侧位移，下部向外挤出，开挖面位移示意图如图10所示。由此可见，对于淤泥地层而言，由于地层支撑能力较差，开舱作业极易发生地层流动，导致地面塌陷等问题，故不适合带压进舱作业。

图10 淤泥地层开挖面位移示意图(单位: m)

1.5 合理换刀区间判断

根据上述数值计算结果，基于全土柱理论计算隧道全线大致上覆荷载大小，结合隧道穿越地层围岩环境，将上覆荷载大小与数值计算得到的最大荷载进行对比，初步判断隧道区段是否适合带压进舱作业。

最大覆土厚度计算方法如下：

1)地下区段： ①对于淤泥地层，根据前文所述，隧道穿越此地层不适合带压进舱作业。②对于圆砾土地层，上覆地层主要为素填土、淤泥和圆砾土层，考虑最不利工况，采用砾砂天然重度(上覆地层中最大天然重度)计算上覆荷载。③对于强风化泥质砂岩地层与中风化泥质砂岩地层，按上覆地层中重度最大地层进行考虑。④对于复合地层，出于对安全性的考虑，将开挖断面视为更弱的地层。

2)水下区段： ⑤地层重度采用浮重度，计算方法与地下区段相同。⑥同时考虑水压力。水压力

σw=αγwhw。

(1)

式中：α为土的渗透系数确定的经验数值；γw为水的容重；hw为水位距刀盘顶部距离。

安全性考虑计算时α的值取为1，海水按照水的重度10 kN/m3计算。即隧道上部覆土高度

(2)

式中hi为上覆各地层厚度(计算时加上初始覆土高度5 m)。

⑦求解最大上覆土厚度

(3)

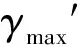
根据数值计算结果，圆砾土地层最大上覆荷载为0.3 MPa，强风化泥质砂岩地层最大上覆荷载为0.56 MPa，中风化泥质砂岩地层最大上覆荷载为0.9 MPa，可计算出地下区段最大上覆厚度对应为20.46、29.89、40.86 m，水下区段最大上覆厚度对应为10.50、21.10、32.04 m。

结合狮子洋隧道实际地层情况，将隧道划分为穿越淤泥层区、圆砾土地层区、强风化泥质砂岩区以及中风化泥质砂岩区。对不同区段按照准许最大上覆土厚度为界限划分，当隧道埋深小于此界限时视为安全，即适合带压进舱换刀作业。将隧道全线大致划分出可以进行带压换刀操作的区间，如图11所示的红色区域。实际施工时可按初步确定的适合带压进舱作业的断面区间为参考，规划带压进舱作业位置。

图11 隧道全线适合带压进舱作业断面示意图

2 实际工程带压换刀分析

狮子洋隧道施工过程中在掘进至第375环时进行了为期7 d的带压进舱换刀作业。第375环断面地质剖面图如图12所示，此处隧道埋深32.09 m，隧道主体穿越中风化泥质砂岩地层，地下水位在4.56 m。上部覆土以淤泥及砂性土层为主，渗透性强。地表由上至下的地层分别为： 1.5 m素填土层、4.92 m淤泥层、3.18 m中砂层、1.04 m淤泥层、0.99 m砾砂层、7.34 m淤泥层、3.36 m圆砾层、3.38 m强风化泥质砂岩以及隧道上部2.38 m的中风化泥质砂岩。

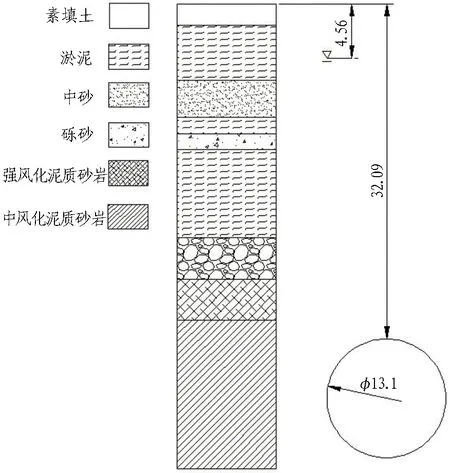
图12 第375环断面地质剖面图(单位： m)

2.1 施工中换刀方案

实际施工时采用基于极限平衡法的楔形体模型计算带压进舱的最小支护压力，指导换刀时的气压设置。根据改进后的楔形滑块[2,21]进行力学分析，实际工程中根据模型计算结果，并考虑施工余量，最终确定开挖面的最小支护压力为0.3 MPa。带压进舱施工时的具体情况见表3。

当舱压设置为0.3 MPa时，隧道刀盘切口位置无渗漏现象发生，此时开挖面位移较小，无明显变化，可以基本判断此时开挖面处于稳定状态，且0.3 MPa气压不是最小支护压力。开舱作业第3天开始，逐天减小切口压力，从0.28 MPa降至0.24 MPa，开挖面变形随着气压减小逐渐明显，且此时开挖面开始发生渗漏现象，换刀位置积水，当气压降至0.24 MPa时渗漏现象更明显。调整压力为0.25 MPa时，在进舱过程中液位有所上升，配合排水措施可完成进舱任务，故判断0.25 MPa为第375环断面位置施工最小气压。

2.2 数值方法判断最小气压

根据狮子洋隧道第375环实际地层条件，采用全土柱理论计算此断面下的上覆荷载大小，全土柱理论计算公式为

(4)

式中：γi为各地层重度；i为对应的地层编号；n为上覆地层数。

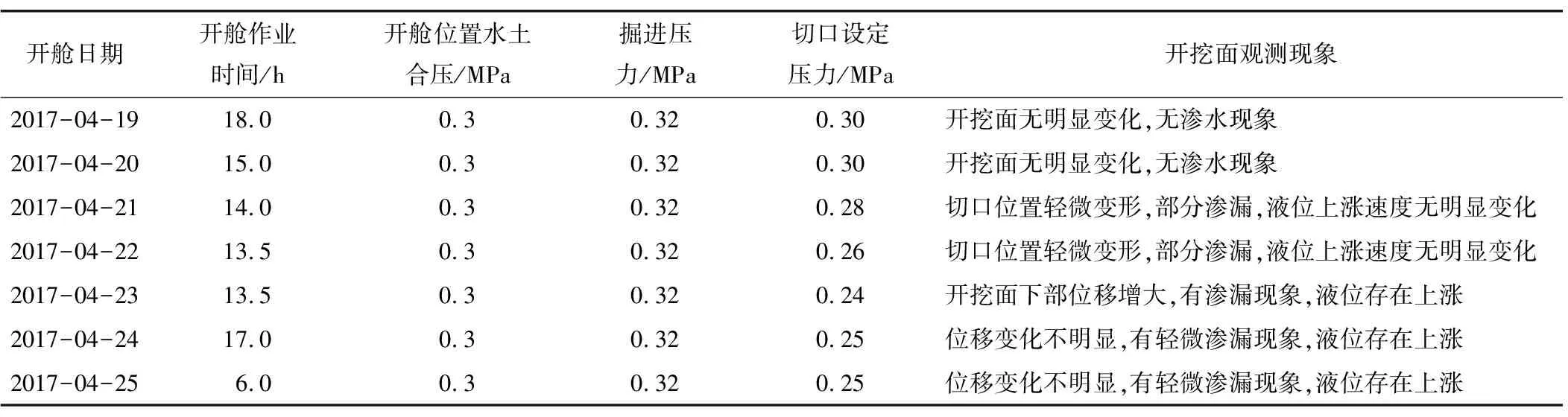
表3 狮子洋隧道第375环带压进舱施工情况

结合如表2所示的地层参数计算得到上覆荷载为506.7 kPa。隧道穿越中风化泥质砂岩地层采用第2节描述的数值模型，设置上覆荷载为506.7 kPa，开挖面荷载从0.36 MPa逐级减小，监测模型开挖面位移变化。开挖面位移与开挖面荷载间的关系如图13(a)所示。

根据数值计算结果可知，当开挖面设置荷载减小至0.22 MPa时，λi的值为3.48，开挖面荷载低于0.22 MPa后位移增长速度过快，此时开挖面可视为失稳。如图13(b)所示，开挖面下部发生失稳，此时最大位移可达10 mm左右。相对于改进后的楔形体滑块模型计算得到的最小支护力0.3 MPa，以及实际施工采用的最小支护力0.25 MPa，数值计算所求的最小支护力偏小。当然，现场施工时出于对安全性的考虑，此时的气压舱舱压并不是开挖面处于极限状态下的最小压力。

3 结论与建议

3.1 结论

本文依托狮子洋隧道工程，采用数值计算与实际施工对比分析的方法，对隧道带压进舱可行性进行研究，得出以下结论：

1)结合实际施工实例证明，本文提出采用数值模拟的方法求解最大上覆荷载后，对比断面上覆荷载大小，选取适合带压进舱作业断面的方法是可行的。

2)根据狮子洋隧道施工中穿越的圆砾土、强风化泥质砂岩以及中风化泥质砂岩3种地层，计算出地下区段最大上覆厚度对应为20.46、29.89、40.86 m，水下区段最大上覆厚度对应为10.50、21.10、32.04 m，淤泥地层不适合进舱作业。最后，根据计算结果给出适合带压进舱作业的参考区间。

3)以实际施工时隧道第375环位置带压进舱换刀为实例，理论计算方法所得最小支护压力偏大，数值计算方法所得最小支护压力偏小，但更接近实际极限情况。

3.2 建议

1)对隧道全区段合理带压进舱作业断面的判别倾向于安全，可作为施工阶段规划停机位置的参考。

2)施工时如需在判别为不适合带压进舱的作业区段停机进舱，可根据实际断面状况进行试算，并针对数值计算结果适当提高气压舱舱压，以达到进舱的目的。