轨道几何动态惯性测量误差评估方法

2022-06-08陈仕明侯智雄王昊魏世斌秦哲程朝阳李颖赵延峰

铁道建筑 2022年5期

陈仕明侯智雄王昊魏世斌秦哲程朝阳李颖赵延峰

1.中国铁道科学研究院研究生部，北京 100081；2.中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081

由于列车频繁通过、道床变形、路基沉降等因素的综合影响，铁路轨道状态逐渐恶化，因此，轨道几何状态的准确测量对行车安全具有重要意义。世界各国用来测量轨道不平顺的方法可归纳为弦测法和惯性基准法两大类，其中以加速度积分与位移相加法为代表的惯性基准法应用于多个国家的轨道检查车，是轨道动态测量的主要手段［1］，相关学者对其进行了广泛研究［2-4］。Weston 等［5-6］讨论了采用安装在构架上的陀螺仪进行轨道动态测量的可行性，指出该方法测量结果在高频部分有一定衰减，在低速条件下比加速度计精度高。Heirich 等［7］尝试在运营车上安装MEMS（Micro Electromechanical System）惯性传感器，通过惯性测量方法观测轨道特征，并分析了惯性传感器的动态特性。

惯性传感器是动态测量的核心传感器。受到零偏不稳定性等随机噪声、车辆振动和电磁干扰产生的高频噪声以及其他有害信号分量的影响，信号滤波的预处理方法对测量精度影响较大［8-9］。为达到系统实时性要求，杜建邦等［10］采用了一种降噪技术，通过使用自适应滤波来提高信噪比，具有较高的滤波精度。在此基础上，Alam［11］等提出了使用可变带宽的自适应滤波预处理技术。Bhardwaj 等[12-13]针对轨道测量应用场景，提出了一种基于FFT 的滤波器最佳截止频率分析方法。由于在轨道检测车上采用空间距离触发采样，Chia、Ward、魏世斌等［14-16］认为惯性传感器的非均匀采样会增加噪声并降低采样信噪比，需要选取特定截止频率的低通有限脉冲响应（Finite Impulse Response，FIR）滤波器。

惯性传感器的积分漂移是动态测量的主要误差来源，因此传感器随机噪声直接决定了长波不平顺测量的准确性。而不同波长、传感器噪声系数、行车速度与测量精度的复杂对应关系仍缺乏有效讨论，惯性传感器选型和截止速度的设定均需要相关理论进行指导。本文从工程应用角度出发，讨论两类动态测量方法在不同行车速度和噪声系数下的表现，提出动态测量信噪比，并对系统在理想条件下的测量准确性进行评估。

1 检测算法

惯性基准法基于惯性测量原理，其基本原理已经发展成熟。传统惯性基准法以加速度计为主要传感器。随着传感器技术的发展，光学陀螺仪的精度和稳定性有了极大提升。惯性基准法目前有基于加速度和基于角速度两类主要模式。

以测量高低不平顺为例进行研究。如图1 所示，将检测系统结构简化为一系悬挂系统。图中：φ为轨道俯仰角，即轨道表面切线方向与大地基准线的夹角；φb为惯组（Inertial Measurement Unit，IMU）点头角；az为轨面的法向加速度为高低不平顺的测量值为轨面高低不平顺Z关于时间t的2阶微分为里程x关于时间t的2阶微分；δV为激光摄像组件输出位移。

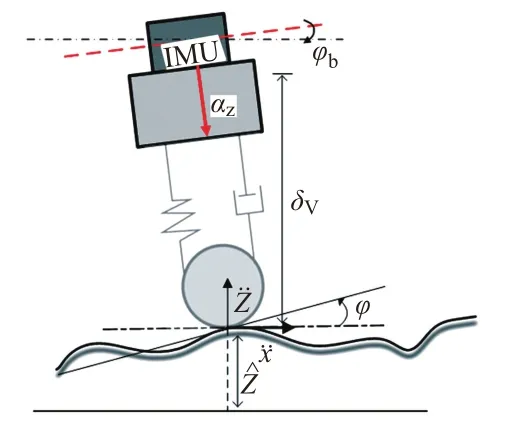
图1 惯性基准法示意

1）加速度测量法

惯性基准法主要利用垂向加速度计测量IMU 载体相对于大地基准的位移变化，用激光摄像组件测量检测梁相对轨面的垂向位移。根据图1 的几何关系，高低不平顺测量值的计算式为

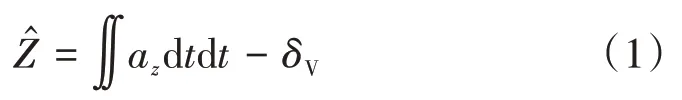
实测数据表明，转向架垂向加速度通常在10g以内。由于垂向加速度敏感值与波长的平方成反比，测量200 m 长波不平顺时加速度往往低于10-3g，因此要求加速度计需要具备低带宽下限、高线性度、低噪声等特性。

2）角速度测量法

根据曲线积分原理，对轨道俯仰角φ进行空间域积分，可实现对高低不平顺的测量。此时高低不平顺测量值的计算式为

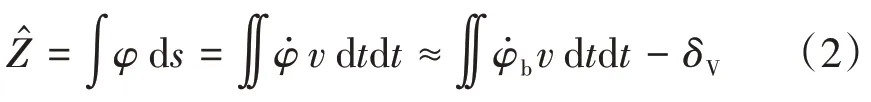
式中：s为距离；v为车速（检测速度）。

由于检测梁与轨面间存在相对振动，角度φ难以用传感器直接观测，一般用检测梁的点头角度φb近似作为轨道倾角φ。对角度进行空间域积分并与δV合成计算，可以完成对高低不平顺的近似测量。

2 传感器数据分析

选取综合检测列车在某无砟轨道区段的实测数据，对比车速350 km/h 条件下车体与构架垂向加速度功率谱密度（Power Spectral Density，PSD）曲线，见图2。其中理论加速度为测量的轨道不平顺递推得到的理论敏感值。

图2 垂向加速度功率谱密度曲线

从图 2 可知：①PSD 曲线在 32 m 和 5 m 处有明显峰值，分别是32 m 简支梁动态挠曲变形和轨道板的变形所导致的典型特征周期性不平顺。②对悬挂系统导致的动态响应衰减值进行对比，50 m 以内的高频区段车体减振衰减为25 ～27 dB；构架加速度在5、32 m处与理论加速度基本一致，在40 ～100 m 区段有明显衰减，最大约为7 dB。故最大衰减幅度为44%。

由于现有轨道检测系统的惯性传感器与构架固连，结合上述分析可知，构架加速度与理论敏感值之间有较好的对应关系。以此为基础，可以进一步讨论轨道检测系统的理论误差。

3 检测系统误差分析

3.1 惯性传感器理论值

设定轨道高低不平顺Z是幅值为A的正弦函数，其表达式为

式中：λ为轨道不平顺波长。

若不考虑悬挂特性，认为惯性传感器能够直接反映轨道平顺性变化。根据式（1），加速度测量法中加速度计测量理论值可表示为

假设测量系统的精度要求为1 mm，即A =1 mm，不同检测速度和波长条件下传感器敏感值见表1。可以看出：当检测速度为50 km/h，轨道不平顺波长为120 m 时，理论加速度为5.40×10-5g，角速度为2.18×10-3°/s；1#和3#分别对应传感器理论敏感值最大值和最小值。惯性基准法要求加速度计动态范围约为1.6×105，要求陀螺仪动态范围约为3.2 × 104。从式（4）和式（5）中可以看出，加速度测量法受到检测速度的影响较大。此外，若要求低速下（50 km/h）测量精度达到1 mm 以内，则加速度分辨率要高于5 × 10-5g，陀螺的分辨率要高于1 × 10-3°/s。

表1 不同检测方法和波长条件下传感器敏感值

3.2 随机噪声标定

陀螺仪、加速度计和其他传感器的零偏都可以在初始校准期间归零，但零偏会随着时间产生漂移。这主要是由于温度变化，也可能是因为电源电压变化、环境因素或材料老化［15］。

目前评价陀螺仪性能的关键指标是零偏稳定性，即零偏平均值随平均时间的变化，但可能会淹没在角速率白噪声或其他附加漂移中［10］。Allan 方差可以在时域上对频域特性进行分析。采用该方法对陀螺仪输出数据构成的一个样本空间进行处理，能更准确地辨识出陀螺仪各项误差的系数［8］。

对某型光纤陀螺仪，静置IMU，连续采集4 ～5 h的数据并进行Allan 方差分析，绘制标准差对相关时间的双对数曲线，见图3。

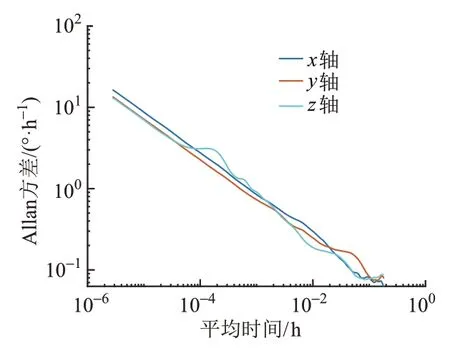
图3 陀螺仪Allan方差标定结果

根据Allan 方差定义，利用图3 计算可知，该光纤陀螺仪的角度随机游走标定参数为0.02°/h1/2，角速度随机游走误差标定参数为0.163 °/h3/2，零偏不稳定性为8.41×10-2°/h。采用同样方法标定振梁加速度计，得到速度随机游走标定参数为1.93× 10-3gm·s-1·h-1/2，零偏不稳定性参数为4.38×10-6g。Allan 方差计算得到的零偏不稳定性与厂家提供的零偏稳定性指标有对应关系，反映器件在极端理想条件下的性能极限，一般比后者低一个数量级。

光纤陀螺仪的零偏稳定性指标σ10s为1 °/h（10 s平滑）。实际情况下陀螺仪的输出常常以白噪声为主，在这种情况下，σ10s与白噪声σN之间的关系近似为［11］

式中：T10s=10 s。

3.3 随机噪声模型

为分析传感器噪声系数对测量系统的影响，对传感器噪声进行建模。惯性传感器的残余误差是影响测量精度的重要误差源，主要包括加速度计、陀螺仪的零偏误差与比例因子误差。而在当前技术条件下，比例因子误差等动态误差相较于零偏为小误差项，在加速度计的随机噪声建模中只考虑零偏误差和速度随机游走噪声；光纤陀螺仪零偏不稳定性较小，在陀螺仪随机噪声建模中只考虑角度随机游走和角速率随机游走，即可大概反映噪声的统计特性。

以陀螺仪为例，设定传感器的随机误差为sm，表达式为［17］

式中：wN(t)为角度随机游走噪声；wK(t)为角速度随机游走噪声；b（t）为噪声wK(t)的积分。

3.4 动态测量噪声传播模型

系统测量精度不仅受IMU 随机噪声影响，还受检测速度和不平顺波长的复合影响，因此须探究有效的评估手段。根据线性系统理论，一个宽平稳随机信号输入至线性时不变系统，其输出信号也是平稳的。根据式（1）与式（2），动态测量系统为线性时不变系统，传感器噪声传播也具备宽平稳特性，在此基础上展开进一步分析。

采用式（7）的模型，对理想加速度或角速度数据进行加噪，并根据式（1）与式（2）计算测量结果。采用蒙特卡洛法，计算N次（N→∞）测量结果的误差标准差，作为随机噪声经过测量系统后的积分漂移误差。统计两类惯性基准法的积分漂移误差的标准差随时间的变化。惯性基准测量法噪声传播模型见表2。其中，ε、σc均为常数。

表2 惯性基准测量法噪声传播模型

由表2 可知：信号在n次积分后的误差标准差与时间t的n次方正比；加速度测量法的测量误差主要与时间有关，角速度测量法不仅与时间有关，还与检测速度正相关。

激光摄像组件的离散测量精度为0.1 mm，且不会随着时间增长而增加，相较于IMU 的积分漂移误差可忽略不计，并不是动态测量的主要误差源。

为综合分析两类惯性基准法的测量精度，以测量信噪比（Signal‐Noise Ratio，SNR）为指标，即理论敏感值S与测量随机噪声N的比值，表达式为

式中：R为信噪比。

两类惯性基准法的惯性传感器敏感值由式（4）和式（5）给出，测量随机噪声参见表2。由于惯性传感器噪声以白噪声为主，仅考虑角度随机游走与速度随机游走，则加速度测量法的测量信噪比Ra和角速度测量法的测量信噪比Rω的计算式分别为

式中：b=A(2π/λ)2；T为经过一个轨道不平顺周期所需的时间，T=λ/v。

从式（9）中可知，惯性基准法的测量信噪比与速度和轨道不平顺波长、幅值直接相关。

测量信噪比仅能在理想状态下对于两类惯性基准法的测量精度进行定性评价。由于列车一系、二系悬挂对振动响应的不同频段会带来不同程度的衰减，实际传感器敏感值会更低。仅讨论传感器安装于构架时，由于构架减振效果更弱，测量信噪比可用于对比在不同传感器噪声系数的条件下两类惯性基准法测量精度的差异。

设定系统精度指标为1 mm，IMU 的随机噪声系数为Allan 方差标定值，考虑两种工况：工况1 为加速度测量法的速度随机游走取1.93×10-3gm·s-1·h-1/2；工况2为角速度测量法的角度随机游走取0.02°/h1/2。根据式（9）计算不同检测速度和波长下两类方法的测量信噪比。为了对比，又计算了角速度测量法的角度随机游走取0.01°/h1/2（工况3）下的测量信噪比。测量信噪比随检测速度和波长的变化曲线见图4。

图4 测量信噪比的变化曲线

由图4 可知：①两类惯性基准法的测量信噪比随检测速度降低而衰减（其中加速度测量法衰减得更为迅速），随波长增加而缓慢降低。②加速度测量法同时受检测速度与时间的影响，角速度测量法仅受时间的影响。③低速下，角速度测量法的精度更高；高速下，加速度测量法的精度更高。④工况1 和工况2 的测量信噪比在v= 85 km/h 处接近。⑤将陀螺仪的角度随机游走噪声指标从0.02 °/h1/2（工况2）提升至0.01 °/h1/（2工况3），角速度测量法的测量信噪比提升了约3 dB。

在实际应用中，检测速度降至30 km/h 以内时，加速度测量法对于40 m 以内短波不平顺的测量结果发生了明显漂移。30 km/h 对应加速度测量法的测量信噪比为0 dB［参见图4（a）］，则以0 dB 作为轨道不平顺能否有效观测的阈值，当前速度记为截止速度。对于角速度测量法，现有传感器对应有效测量的截止速度约为5 km/h（工况2）；若将陀螺仪角度随机游走噪声提升至0.01°/h1/（2工况3），截止速度可降至0 附近，则角速度测量法可实现0 速测量，在地铁等需频繁停车的工况下有非常好的应用前景。

检测系统截止速度随波长的变化曲线见图5。可知：①截止速度随波长增加而增加。②角速度测量法的截止速度明显低于加速度测量法。对于200 m 波长的轨道长波不平顺，加速度测量法（工况1）、角速度测量法（工况2）的截止速度分别为75、65 km/h。将陀螺仪角度随机游走噪声提升至0.01°/h1/2（工况3），截止速度可降至40 km/h，测量精度提升较为明显，更能满足应用需求。根据式（6）可知，对应动态检测系统的零偏稳定性指标为0.2°/h（10 s平滑）。