混合不确定条件下的飞行器级间分离可靠性分析

2022-06-08聂兆伟张海瑞

国防科技大学学报 2022年3期

聂兆伟，王浩，秦梦，张海瑞

(1. 中国运载火箭技术研究院，北京 100076； 2. 南京理工大学机械学院，江苏南京 210094)

高马赫数飞行器级间分离过程是发射任务的关键环节，通常包括热分离和冷分离两种方式，其功能是完成飞行器飞行过程中的预定工作、且在后续飞行中将子级分离，减小结构重量、发挥性能优势、提升飞行速度[1]。高超声速飞行器在实施级间分离时受到诸多不确定性因素影响[2]，如质量特性偏差、初始条件偏差、气动特性偏差以及动力特性偏差等，尤其是在大气层内实施分离时，受大气密度和飞行速度影响，飞行器面临严酷的动压环境，各类偏差影响显著，两体分离存在较大技术风险，制约了飞行可靠性水平的进一步提升[3-4]。

常规飞行器分离分析方法通常是基于参数极限偏差组合进行的，无法反映系统参数的内在可变性以及对系统认知的不完整性，难以满足分离方案精细化设计需求，甚至在某些情况下导致分离方案过于复杂，影响了飞行器总体性能的进一步提升。

针对这一问题，目前的研究趋势是将不确定性注入分离动力学仿真模型，实现分离方案的精细化分析[5-6]。国内外学者将概率方法与分离运动仿真相结合，系统研究了随机不确定性对分离过程的影响[7-8]，Roshanian等[9]将蒙特卡洛方法与分离运动仿真相结合，给出了分离运动参数的包络曲线。李慧通等[10]结合级间冷分离和热分离的优点，设计了一种新型级间分离方案，采用蒙特卡洛方法分析了分离体的相对运动。

蒙特卡洛方法具有无偏性与非侵入性，适用于求解隐式非线性问题，在级间分离精细化分析中有着广泛的应用。然而高超声速飞行器在大气层内实施分离过程中，对某些关键参数依然存在认知的不完整性，如气动特性偏差，无法采用概率理论对其精确描述，为准确量化飞行器级间分离过程中系统参数的内在可变性以及对系统认知的不完整性，需要进一步开展基于概率-非概率混合模型的飞行器级间分离可靠性分析方法，为飞行器分离方案的精细化设计提供决策支持。随机不确定性通常采用概率理论描述，发展相对成熟[11-13]。认知不确定性通常采用非概率理论来描述，包括区间理论[14-15]、证据理论[16-17]、模糊理论[18]等。工程应用中，考虑天地不一致性，某些参数仅能给出上下边界，无法给出边界内的相关分布信息，因而，区间理论适用性更为广泛，本文选用区间理论描述认知不确定性。

为准确量化飞行器级间分离过程随机不确定性和认知不确定性的综合影响，采用概率-区间混合模型描述分离过程中系统参数的内在可变性及对系统认知的不完整性。以某轴对称式飞行器级间冷分离方案为研究对象，根据轴对称级间分离结构的几何特点，设计了一种快速碰撞检测模型，为可靠性分析提供支撑。进而，将混合可靠性分析模型转化为随机可靠性分析的无约束优化问题，采用高效全局优化和自主学习Kriging方法实现无约束优化问题的高效求解，给出飞行器分离任务可靠性的区间范围。

1 分离动力学建模

以高马赫数飞行器级间冷分离方案为研究对象，建立分离动力学模型。两体级间分离过程中，上面级受到自身重力、气动力及两体分插拔脱力的影响，下面级受到自身重力、气动力、两体分插拔脱力、发动机残余推力以及反推发动机推力等因素影响。图1为飞行器级间冷分离示意图。

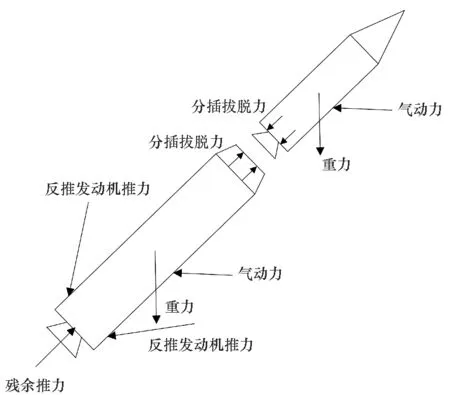
图1 级间冷分离Fig.1 Stage cold separation

飞行器组合体、上面级和下面级的弹体系原点与对应质心重合，x轴与对应弹体轴线重合，y轴在弹体纵向对称面内，且垂直于x轴；定义飞行器分离系与分离开始时组合体的弹体系一致。级间分离刚体动力学方程为：

(1)

其中：分析对象可以是上面级、下面级或者两者的组合体，m是各分析对象对应的质量；vx,vy,vz是各分析对象对应的速度矢量在分离系下的速度投影；Fx,Fy,Fz是各分析对象受到的合力在分离系下的投影；ωx1,ωy1,ωz1为分析对象转动角速度在弹体系中的分量；Ix1,Iy1,Iz1为分析对象相对其弹体系的转动惯量。此外，补充建立角速度与欧拉角、位置与速度之间的关系，如式(2)所示。

(2)

进一步给出分析对象弹体坐标系到分离坐标系的转换矩阵。

(3)

飞行器级间冷分离过程，上面级发动机喷管需从下面级壳体内拔出，需重点关注两体运动关系及相对距离，避免两体发生碰撞。碰撞检测是分离仿真的难点之一，其关键在于计算空间两体的最小间隙距离，结合干扰式轴对称级间分离结构的几何特点，设计了一种快速碰撞检测方法，干扰式分离过程中两体分离最小间隙距离一般有两种可能形式[19]，如图2所示。

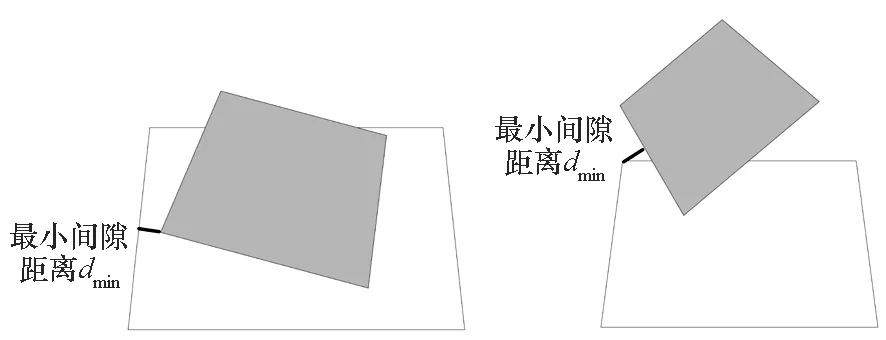
图2 飞行器干扰式分离Fig.2 Vehicle interfering separation

结合串联干扰式分离的特点，危险体截面为上面级发动机喷管的下底边和级间段的上底边，故特征点应在危险体截面上平均选取。这里将上面级发动机喷管和级间段简化为一个圆台体，重点关注各个特征点到圆台体的最短距离，记圆台体上表面圆心坐标为A，半径为rA；下表面圆心坐标为B，半径为rB；特征点坐标为P，由于特征点到圆台体的最短距离d一定在平面PAB内，此时三维空间问题转化为二维平面问题，如图3所示。

图3 不同区域最短距离Fig.3 Minimum distance in different regions

为保证特征点到圆台体最短距离的计算完备性，根据圆台体的几何特点，将特征点所在区域划分为10个不同的区域，其中3、4、8、9区的最短距离为特征点到圆台体内外表面的最短距离，其他区域最短距离为特征点到圆台体上下低边的最短距离。特征点P到圆台体中轴线的距离rP，圆台体截面底边夹角θ及8、9、10区分界点C、D可进一步表示为：

(4)

结合所在区域的特点，给出特征点P到圆台体的最小距离ds，如下节中10个情况下的ds公式所示。进而，选取危险截面所有特征点的最小值为某一时刻两体分离的最小间隙距离dsmin

dsmin=min{dsi},i=1,…,N

(5)

其中，N为危险截面特征点的数量。采用四阶龙格库塔方法进行两体分离动力学仿真，定义从分离开始到上面级起控过程中，两体最小间隙距离最近的时刻为危险时刻，在上面级发动机喷管从级间段拔出过程中，为避免时间步长过大导致漏失危险时刻，需要在危险区域附近缩短时间步长，识别两体分离过程中的危险时刻，取时间步长为0.002 s。考虑数值误差和安全系数的影响，给定最小间隙阈值εd，若从开始分离到上面级起控过程中，所有时刻最小间隙距离的最小值大于阈值εd，则判定分离过程中未发生碰撞。

2 分离可靠性建模

飞行器分离过程存在多种故障模式，其中较为典型的故障模式包括两体碰撞及上面级起控失效。前者由于两体干涉碰撞，上面级部分功能失效，采用上述碰撞检测方案快速给出两体分离过程的最小间隙距离。后者可能由于上面级起控时角速度过大，上面级不可控，分离任务失败。

1)若AP·AB<0,rP≤rA，则P在1区，从而

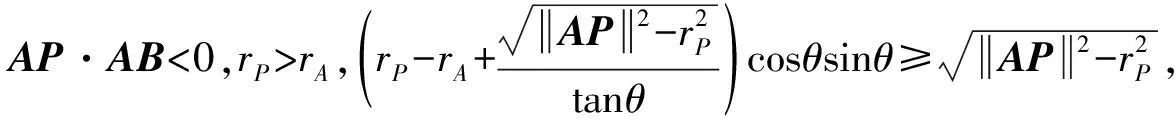
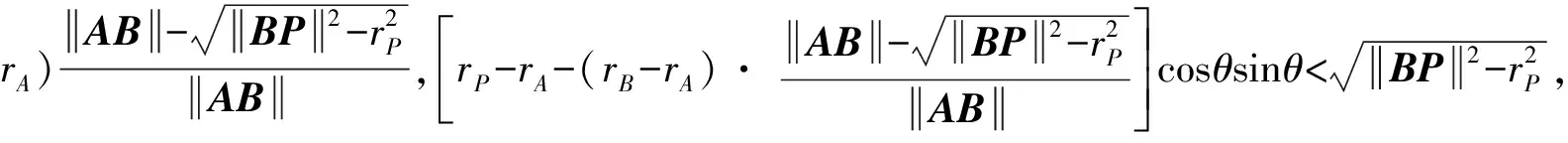
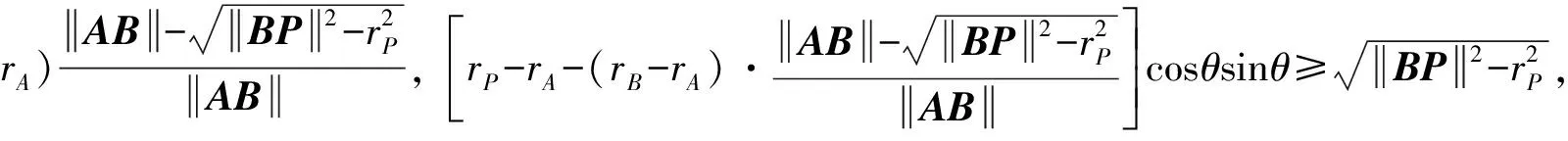
6)若BA·BP<0,rP>rB，则P在6区，从而

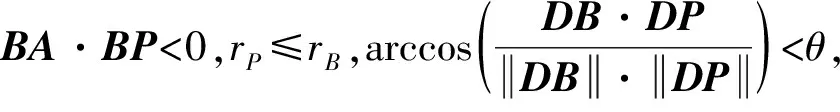
针对上述两种典型失效模式，分离过程中的随机不确定性参数向量表示为X，认知不确定性参数向量表示为Y，则两体分离最短距离为dsmin(X,Y)，上面级起控时的角速度为ω(X,Y)，且这两种失效模式构成串联系统，飞行器级间分离的多故障联合失效域为：

Df={dsmin(X,Y)<εd∪ω(X,Y)>εω}

(6)

式中，εd,εω分别为两体分离最小间隙距离阈值和上面级起控时角速度阈值。进而，分离可靠度为：

R=1-Pr(Df)

=1-Pr{dsmin(X,Y)<εd∪ω(X,Y)>εω}

(7)

3 飞行器概率-区间混合可靠性分析

3.1 概率-区间混合可靠性模型

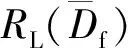
A：随着不断发展，我们也需要更多复合型人才，仅是印刷专业的学生不能够满足企业自身发展的需要。雅昌成立之初的定位就是艺术印刷。正是因为当时的正确选择和清晰定位，才能脱颖而出，成为行业中的佼佼者。关于人才需求，在内部人才培养方面，雅昌把所有利润全部投入到技术的研发和相关人员的培训上；就人才招聘方面，雅昌对人才需求已从印刷类转为艺术类。

考虑认知不确定性Y在某一区间[YL,YU]，分离失效概率上界PfU进一步转化为最大无约束优化问题

maxPr{X|Y∈[YL,YU],dsmin(X,Y)<

εd∪ω(X,Y)>εω}

(8)

同理，分离失效概率下界PfL转化为最小无约束优化问题

minPr{X|Y∈[YL,YU],dsmin(X,Y)<

εd∪ω(X,Y)>εω}

(9)

通过上述推导，将概率-区间可靠性模型转化为随机可靠性分析的无约束优化问题。

3.2 多故障联合可靠性分析

考虑到飞行器分离的多故障联合失效域包含若干功能函数，传统的一次可靠度法(first order reliability analysis method, FORM)等在功能函数最大可能点(most probable point, MPP)进行泰勒展开，在求解非线性多故障联合可靠度问题时会产生较大误差[20]。针对这一问题，Echard等提出了Kriging与Monte Carlo相结合的主动学习可靠性方法(active learning reliability method combining Kriging and Monte Carlo simulation, AK-MCS)的单故障可靠度分析方法，具有很高的效率[21-22]，以此为基础，进一步发展了适用于串联或者并联系统的多故障系统可靠性的主动学习Kriging方法(active learning Kriging method for system reliability, AK-SYS)[23-24]。

以认知不确定性Y在某一区间[YL,YU]为例，结合飞行器级间分离的特点，利用Kriging代理模型将功能函数表达为：

(10)

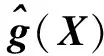
(11)

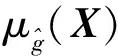
(12)

其中，rT(X)=[R(X,X1),…,R(X,XN)]T是预测点X和训练样本点集XT=[X1,X2,…,XN]T之间的相关函数向量。

结合随机不确定性分布类型及参数，在随机空间中抽取样本点，样本点数量满足条件：

(13)

式中，Pf为多故障联合失效概率。结合Kriging模型能够直接给出预测点均值和标准差的特点，利用概率分类函数评估预测点X的不确定性，式(11)给出了Kriging预测值Gaussian分布特性，以此为基础，Kriging模型的分类失效函数可表达为：

(14)

式中，Φ(·)为标准正态分布函数。

针对多故障联合可靠性分析的特点，进一步给出飞行器级间分离多故障联合分类失效函数为：

(15)

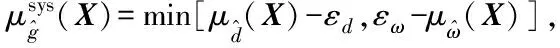
(16)

当Usys函数的最小值大于2时，样本点集的分类失效概率最大值仅为Φ(-2)≈0.022 8，满足收敛要求。

3.3 高效全局优化

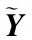
(17)

进一步采用全局优化算法在认知不确定性内Y∈[YL,YU]寻找多故障联合可靠度的最大值和最小值。

针对这一无约束优化问题，由于多故障联合可靠性分析嵌套在优化过程中，如何高效求解无约束优化问题是混合可靠性分析的关键环节之一。Jones等[25]将全局优化算法与代理模型相结合，进一步发展了高效全局优化(efficient global optimization, EGO)方法，其关键在于优化求解期望改善函数(expected improvement function, EIF)。以求解分离失效概率下限为例，定义期望改善函数为：

(18)

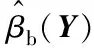
(19)

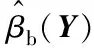
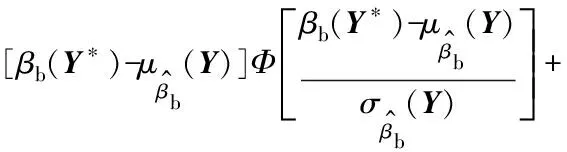
(20)

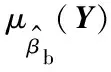
PfL=Φ[βb(Y*)]

(21)

同理，将分离失效概率上界的最大值优化问题转化为最小值优化问题，即可通过上述方法给出结果。

4 实例结果

以某低空高超声速轴对称式飞行器级间冷分离方案为应用对象。考虑到分离过程中系统参数的内在可变性及对系统认知的不完整性，给出如表1所示的随机不确定性分布描述和认知不确定性分布描述。

表1 随机不确定性分布类型及其参数

通过试验数据和工程经验确定随机不确定性参数的分布，选取工程上重点关注的若干参数作为随机不确定性参数，进而通过灵敏度分析可知，初始俯仰角速率和气动特性偏差对两体分离最短距离d和上面级起控时的角速度ω有较大影响，同时这两者在工程上难以采用概率理论精确描述，因而将其处理为认知不确定性。初始俯仰角速率dφ0∈[-1 ((°)/s),0]，气动特性偏差Wqd∈[-0.15, 0.15]。

针对飞行器级间冷分离方案的特点，Kriging模型选用二阶多项式回归模型作为回归函数。对于多故障联合可靠性分析问题，初选阶段选用常用的拉丁超立方采样方法对随机不确定性空间进行均匀采样，Kriging模型选用二阶多项式回归模型作为回归函数。为了验证上述方法的正确性，在随机变量空间选用蒙特卡洛方法抽取106个样本点，进一步在区间分布空间均匀抽取2 000个认知不确定性变量样本，以此获取认知不确定性Y在区间内变化影响下多故障联合可靠度响应的变化范围[5]，分别给出分离高度为36 km条件下的分离可靠性的上下界，见表2所示。

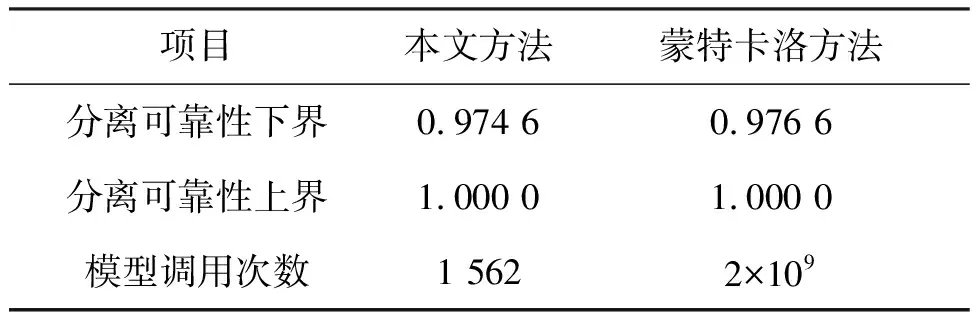
表2 混合不确定性下飞行器级间分离可靠性上下界

表2的计算结果表明，本文方法得到的分离可靠性上、下界结果与采用蒙特卡洛方法的计算结果相吻合，最大相对误差仅为0.2%，这说明了本文方法的正确性。同时，模型调用次数远低于蒙特卡洛方法的分析次数，说明了本文方法的高效性和可行性。进一步，针对低空高速飞行器级间分离的特点，考虑不同高度对分离可靠性的影响，在认知不确定性相同设置条件下，采用本文方法给出25～40 km之间飞行器级间冷分离的系统可靠性，如图4所示。

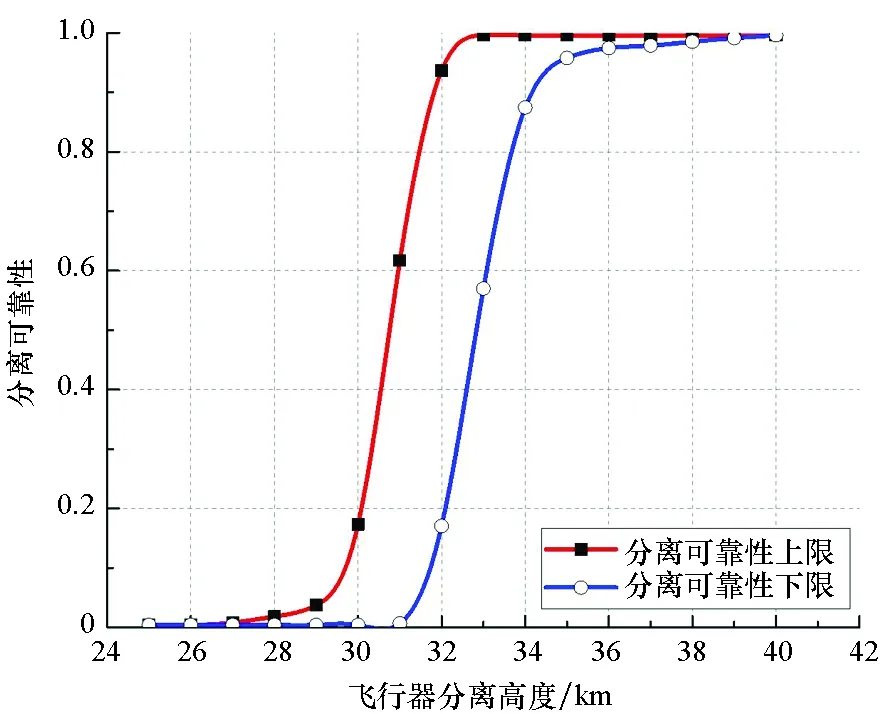
图4 不同高度条件下混合不确定性分离可靠性上下界对比Fig.4 Comparison of maximum and minimum of system reliability with mixed uncertainties under different given different height

图4结果表明，在某些分离高度下，分离可靠性的可能分布区间较大，这表明在当前分离高度进行级间分离时认知不确定性影响显著，需要进一步考虑可能存在的技术风险。从总体趋势来看，飞行器分离高度对分离可靠性的影响显著，由于高超声速飞行器飞行马赫数较大，随着分离高度的降低，承受动压较大，因而气动特性偏差影响显著。以分离可靠性下限为参考，通过控制分离高度可实现两体可靠分离，为飞行器分离方案的精细化设计提供决策支持。