带局部交流函数及自由意志的单领导Cucker-Smale模型的渐近集群分析
2022-06-08赵子玉刘易成
赵子玉,刘易成
(国防科技大学 文理学院, 湖南 长沙 410073)
鸟群、鱼群等自然界的动物具有自组织的群体效果,即:使用局部信息和简单规则便可从无序的状态过渡到有序运动中。匈牙利著名的生物物理学家Vicsek[1]率先提出了一种刻画集群行为的动力学模型;之后, Jadbabaie等[2]基于一定的假设条件从数学的角度严格证明了上述实验的正确性,但这样的行为演化规则过于理想化。因此,2007年Cucker和Smale[3-4]提出了一个非常有实际意义的集群模型,后来把它称为Cucker-Smale模型(简称C-S模型)。这种模型考虑了个体数量以及个体在空间的几何关系。Ha等[5]利用Lyapunov泛函的技巧对C-S模型进行了一个简洁的分析并改进Cucker[3]和Tadmor[6]的结果,Ha发现对于长程相互作用的C-S模型,系统会以指数收敛速度达到无条件的同步,即对任意给定的初值,所有个体的速度会指数收敛到同一值,但对于短程相互作用的C-S模型,要想达到同步性的结果,就需要对初值加以限制。此后,出现了大量的数学模型来研究群体行为[7-10]。
生物学家Ballerin和他的团队在研究鸟类集群时发现每一个鸟只能够直接地影响它周围的六七只鸟,并在一些生物系统比如蚁群、鱼群以及蜂群中发现每个个体主要被其周围个体所影响[11-13]。所以,2016年Cucker和Dong[14]提出了受最小邻居集影响的模型,同年金春银[15]在其博士论文中研究了局部C-S 模型在同步状态附近的大时间行为。
从20世纪80年代开始,生物学家揭示了每一个生命体——小到单细胞组织大到人类都存在着自由意志[16-18]。在此基础上的研究工作有:Cucker[19]在C-S模型中增加了自由意志,其定义的自由意志依赖于跟其他个体的相对速度;2008年,Shen[20]在他的连续HL模型中考虑了自由意志;Dong[21]在2013年研究了具有自由意志的离散HL模型;2016年,李乐[22]在其博士论文中将自由意志引入等级结构中,研究了具有等级结构和自由意志的多智能体复杂系统的集群控制。
除此之外,有科学研究发现在集群运动中广泛存在着领导和跟随关系,例如,Vicsek发现鸽子长途飞行中就存在着这种关系[23]。其他科学家也发现,当几只工蜂发现蜜源,就会回来通知其他蜜蜂一起去采蜜,而这几只有经验的工蜂就会担当领导者的角色[24]。所以基于以上发现,Li和Xue[25]提出了一个离散的集群模型,在这个模型中存在一个全局领导者,它不受其他个体的影响,但其直接或间接地影响着其他个体。
在总结上述研究后发现,人们将局部交流函数引入等级结构中的研究还很少;再直观地想,集群的形成应该和半径有关,而此类结论同样也很少见。因此,本文主要考虑带有局部交流函数及自由意志的等级C-S模型。首先讨论领导者速度变化的情形,然后考虑领导者速度恒定不变的情形,最后给出数值仿真。
1 局部交流函数下的等级结构
1.1 基本定义
考虑两个等级的局部C-S模型,领导者处于第一层级,其位移速度描述为:
(1)
第二层级为N个追随者,其位移速度描述为:
(2)
其中:
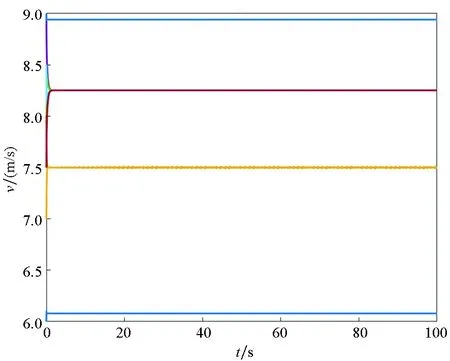
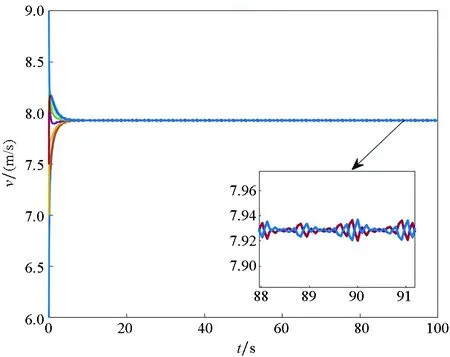
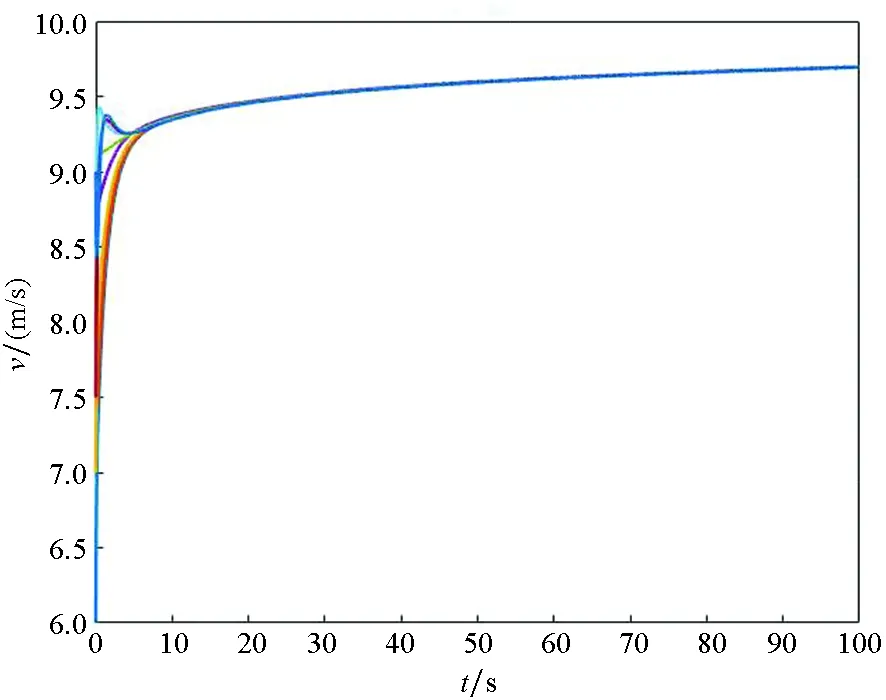
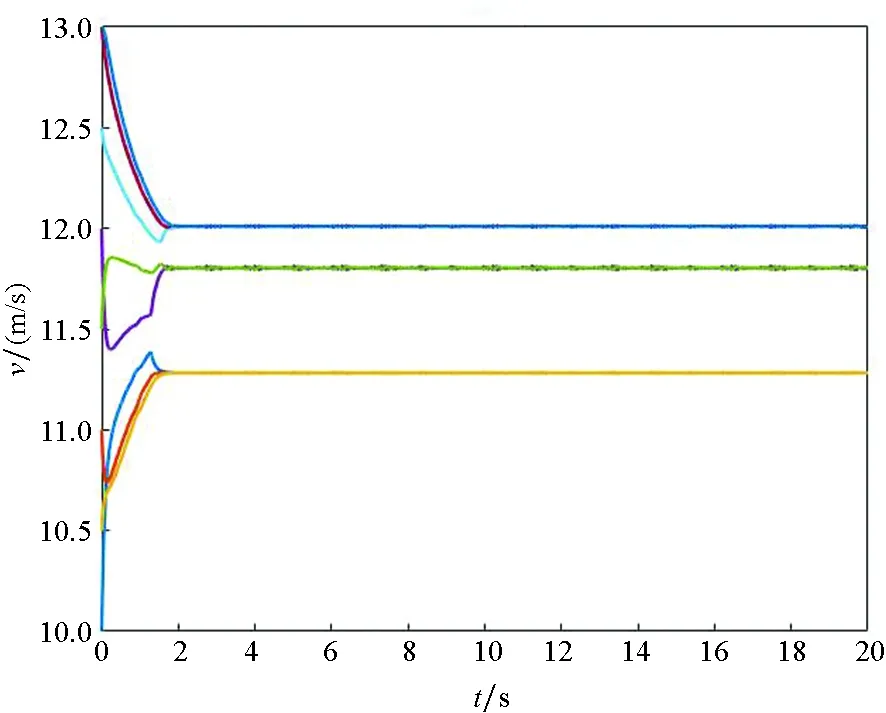
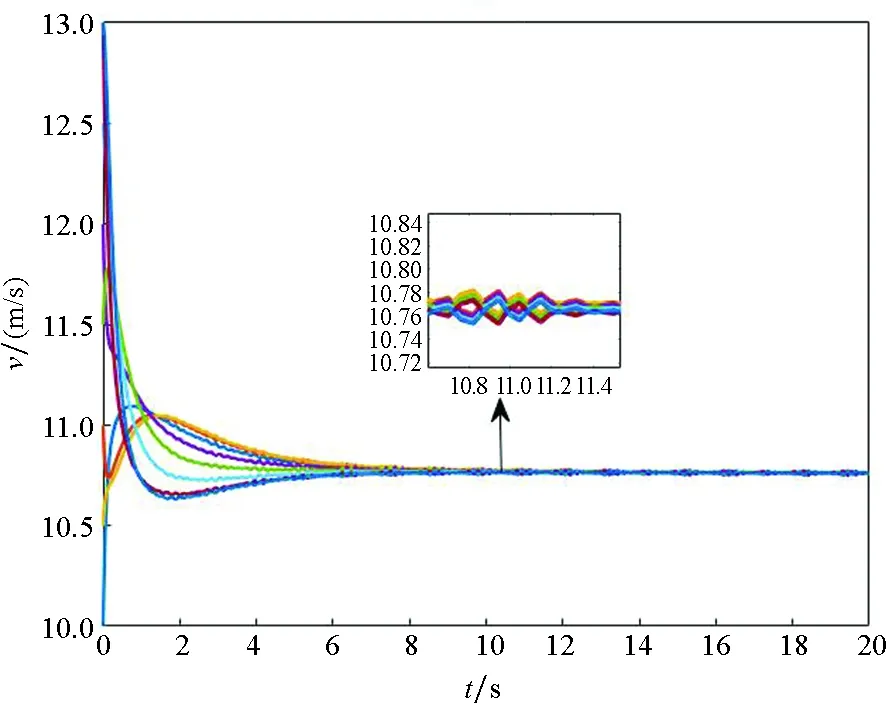
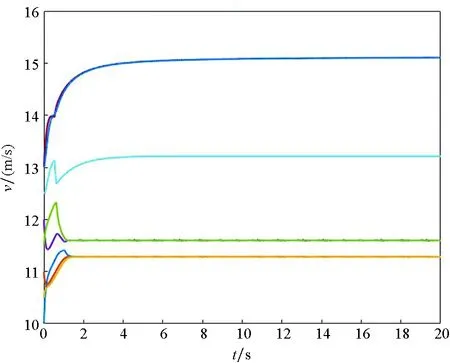
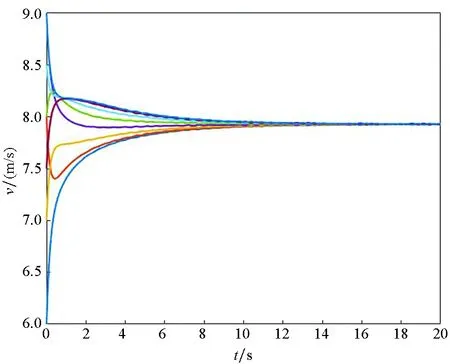
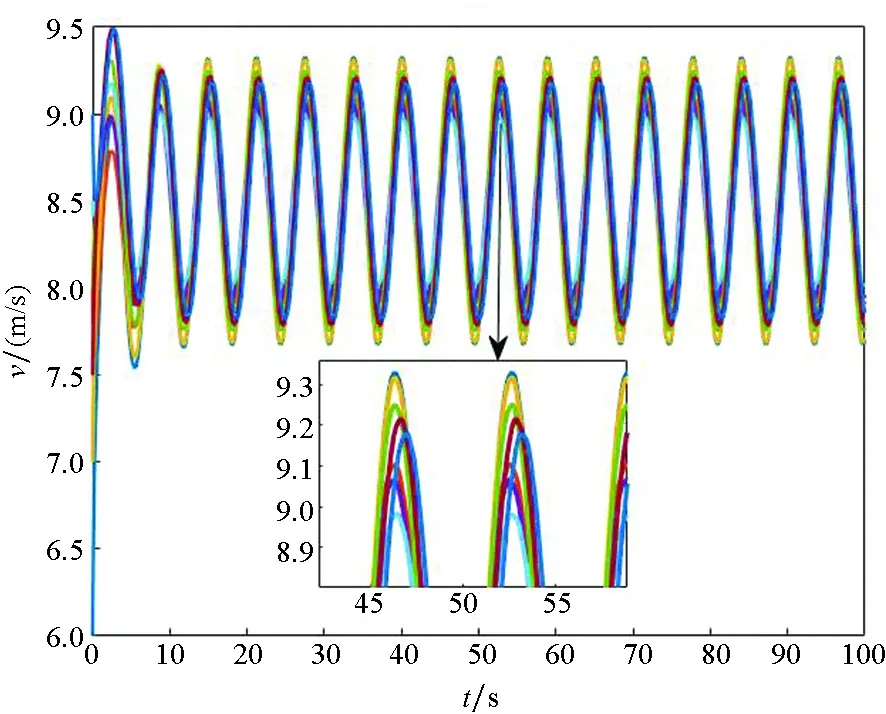
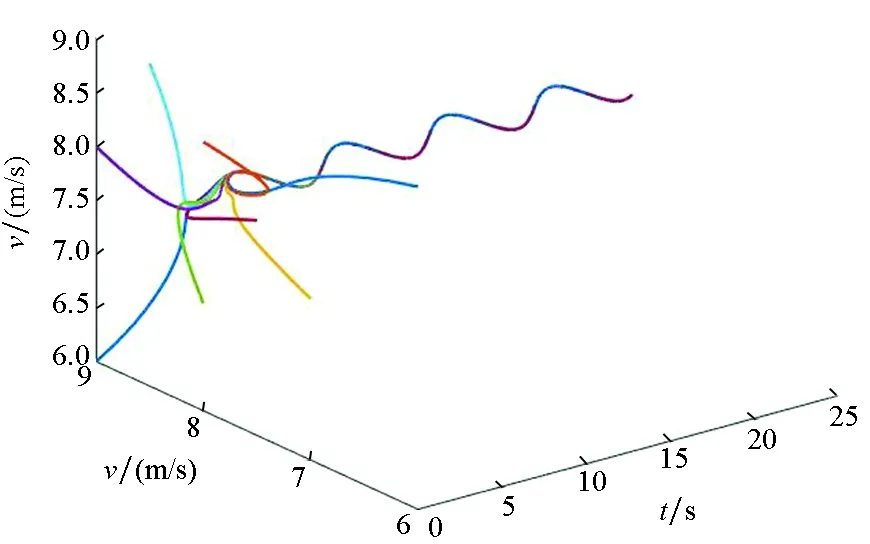
Ni(t)=card{j:|xj(t)-xi(t)| xi∈d,vi∈d,α为通信强度,N={1,…,N},fi(t)为自由意志。 局部交流函数描述为:对给定的交流半径r,小于交流半径有联系,大于交流半径则失去联系,通信函数φ(s)具体表现形式为φ(s)=1/(1+s2)β(0≤β<0.5)或φ(s)≡1。注意到χr(s)≤1,因此进而令对于φ(s)=1/(1+s2)β(β<0.5),r=∞,由已有结论可知其无条件集群[3-6]。 本文主要目的是给出与初值相关的最小半径的充分条件并给予证明。 此模型更加贴近现实,原因为:一是粒子不再是全域交互而是局部信息交互,二是考虑了现实中广泛存在的等级结构,三是考虑了粒子本身固有动力学特性即自由意志。 首先给出集群的定义即位移和速度有界。 定义1多智能系统式(1)和式(2)有渐近解当且仅当其解{xi,vi}(i=1,…,N)满足以下两个条件: 1)速度差关于时间有界,即: 其中vc为一个常向量,C为一个常数。 2)位移差关于时间有界,即: 那么此系统会形成集群。 证明:由局部交流函数可知粒子无法与每个粒子进行交互,因此考虑两种情形——情形1:i∈εp(t); 情形2:i∈εj(t),j≠p,即i处在领导p半径内或其他粒子j半径内,其中εj(t)=card{i:‖xi-xj‖ dV2p(t)=max{‖vi-vj‖} dX2p(t)=max{‖xi-xj‖} dV1(t)=max{‖vi(t)-vj(t)‖} dX1(t)=max{dX1p(t),dX2p(t)} 首先直接计算可得: αvp(t)+fi(t)-fp(t),vi(t)-vp(t)〉 α〈vi(t)-vp(t),vi(t)-vp(t)〉+〈fi(t)-fp(t), vi(t)-vp(t)〉 (3) 又因为 那么可以得到不等式: ‖fi(t)-fp(t)‖-αdV1p(t) (4) (5) 首先在情形1中构造如下能量函数: 对构造的能量函数求导得E′1p(t)≤0,那么有E1p(t)≤E1p(0),化简后有: 对于情形2,可以找到粒子j使得i∈εj(t),即i和j可相互联系,同理构造能量函数: 可知E′2p(t)≤0⟹E2p(t)≤E2p(0),由定理条件得: 式中,CM为系统内粒子间的最大距离。 由χr(s)为递减函数,故有χ(dX1(t))≥χ(CM),那么粒子间的最大速度差估计为: 由Gronwall不等式且当时间趋于无穷时有: 即速度有界,至此已证明了速度位移有界,由定义可知式(1)、式(2)有集群行为。 □ 此小节考虑式(1)、式(2)退化到特殊情形时的等级结构(领导个体速度恒定不变,追随者的动力学模型不变),即: (6) 处于第二等级的为追随者,其位移速度描述为式(2),类似于定理1的结论,便可得到上述模型的最小半径估计。 那么此系统会形成集群。 证明:类似于定理1中式(3)~(5)的推导过程有 故构造能量函数 同理对其求导有: ≤0 故可知E(t)≤E(0),由此可以得到: 那么有dX1(t) 同样由Gronwall不等式且当时间趋于无穷时,粒子最大位移差满足如下不等式: □ 图1的初始信息为(xp,x1,…,x7)=(5,15,25,35,45,55,65,75),(vp,v1,…,v7)=(6,8,7,9,8,8.5,7.5,9),主要说明半径对集群的形成起着至关重要的作用。由模型知速度趋向于平均速度,而图1的平均速度约为7.8,且可知自由意志(v4,v6,v8>7.8)为正起着抑制集群的作用,但图1(c)依旧能形成集群,说明半径比自由意志的作用更大。图2的初始信息为(xp,x1,…,x7)=(44,32,20,56,20,56,68,80),(vp,v1,…,v7)=(10,11,10.5,12,11.5,12.5,13,13),经计算其平均速度约为11.6。由图2(b)可以发现其使得粒子群集群,图2(c)中加入反作用后可以发现其使得粒子分群数量更多,进一步说明了自由意志的作用有正反两方面。另外,两个实验都可发现,粒子群最终速度不会趋于同一值,而是形成一定程度的波动,验证了速度的有界性。图3的初始集同图1,其有无自由意志的对比说明增加的自由意志可以使集群的行为更加复杂,更加贴近现实的复杂集群,也说明考虑带有自由意志的等级结构模型的必要性。图4对数据xp=(5,6),x1=(15,16),x2=(25,26),x3=(35,36),x4=(45,46),x5=(55,56),x6=(75,76),x7=(95,96),vp=(6,9),v1=(8,8.5),v2=(7,7.5),v3=(9,8),v4=(8,7),v5=(8.5,9),v6=(7.5,8),v7=(9,6),f1,3,5,7=(sint/8,cost/8),f2,4,6,8=(cost/8,sint/8) 进行三维仿真,发现最终速度差仍小范围波动。 (a) r=10 (b) r=18 (c) r=18, f4(t)=1/(t+0.1),f6=1/(t2+0.1), f8(t)=e-t 图1 式(1)、式(2)的模拟结果(α=8,φ(s)≡1)Fig.1 Numerical simulation of equation (1) and (2) (α=8,φ(s)≡1) (a) 无自由意志(a) No free-will (b) 自由意志(f6,8(t)=-e-t, f7=-1/(t2+0.1))(b) With free-will(f6,8(t)=-e-t,f7=-1/(t2+0.1)) (c) 反作用自由意志(f6,8(t)=e-t, f7=1/(t2+0.1))(c) Negative free-will(f6,8(t)=e-t, f7=1/(t2+0.1))图2 式(1)、式(2)的数值模拟结果(α=8,r=12.5,φ(s)≡1)Fig.2 Numerical simulation of equation (1) and (2) (α=8,r=12.5,φ(s)≡1) (a) 行为单一集群(fi(t)=0,i=1,…,8)(a) Simple cluster(fi(t)=0,i=1,…,8) (b) 复杂集群(f1,3,5,7(t)=sint;f2,4,6,8(t)=cost)(b) Complex cluster (f1,3,5,7(t)=sint;f2,4,6,8(t)=cost)图3 式(1)、式(2)的模拟结果(α=8,r=18, φ(s)=1/(1+s2)β,β=0.2)Fig.3 Numerical simulation of equation (1) and (2) (α=8,r=18, φ(s)=1/(1+s2)β,β=0.2) 图4 式(1)、式(2)的三维模拟(α=16,r=20,φ(s)≡1)Fig.4 Numerical simulation of equation (1) and (2) (α=16,r=20,φ(s)≡1) 本文利用Lyapunov泛函的方法给出了满足集群的最小半径条件,可以看出,其半径和初始数据中相互通信粒子间的最大速度差、粒子间最大速度差以及自由意志有关,这可以理解为:为满足粒子间通信,半径应有一定的容错范围,在一定时间内将边缘远离平均速度的个体拉回到朝向平均速度运动的方向上,使粒子群最终形成集群。本文用已有的方法研究更加贴近现实的模型,通过分情况讨论以及泛函方法给出了与半径有关的结论,达到了给出半径范围刻画的目的。若有初始位置及出发速度,便可以通过计算得知集群形成的最小半径。本文方法的优点在于将集群的形成与否反应在半径上,使得集群的刻画更加简洁明了,但不可否认的是这种刻画简单粗暴,达不到真正意义上半径的下确界,所以此证明方法只是给出了半径的充分条件,且最终速度差有界并不会趋于0,对于小于最小半径的r可能形成集群也可能不会形成集群,若r→∞则交流函数全时域交互,由已有结论可知其会形成集群,那么考虑半径的大小具有一定的合理性,故下一步的工作在于找到其半径的下界。1.2 局部函数下的一般等级结构
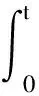

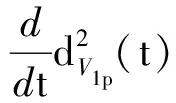
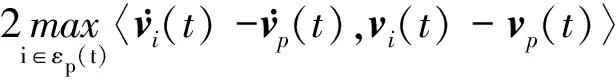
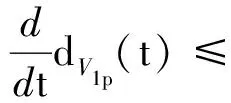
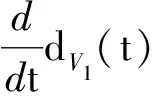

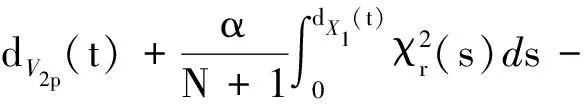
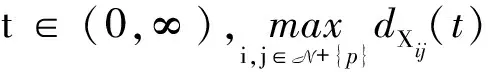
1.3 局部函数下的特殊等级结构
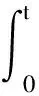
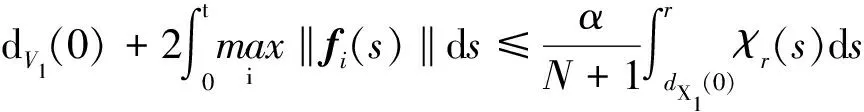
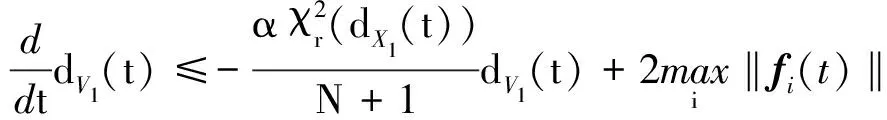
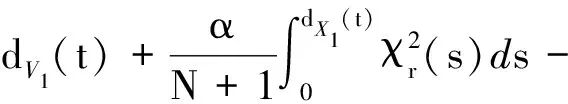
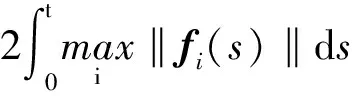

2 仿真结果
3 结论
