基于盲数字接收机与拟合优度的SOQPSK识别算法

张铭宏，沈 雷，卢英俊

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

0 引 言

成型偏移四相相移键控(Shaped Offset Quadrature Phase Shift Keying, SOQPSK) 信号是由相移键控(Phase Shift Keying, PSK)信号演变而来的一种连续相位信号，具有相位连续、包络恒定、频谱利用率高等特点，在卫星通信领域具有广泛应用[1]。但是，卫星通信中，连续相位信号与非连续相位信号频域的相似度较高，难以区分。现有识别算法主要是根据瞬时特征、高阶谱特征、循环谱特征、小波变换后相应信号特征等特征识别连续相位信号与非连续信号。文献[2]提出一种基于瞬时幅度谱的连续相位信号与非连续相位信号识别算法，根据连续相位调制(Continuous Phase Modulation, CPM)信号相位连续的特点来统计信号瞬时幅度谱特征，有效区分了连续相位信号与非连续相位信号，但在低信噪比下，瞬时幅度谱易受噪声影响，识别性能下降。文献[3]采用高阶谱特征的方式进行CPM信号与PSK信号的识别，分别统计信号的平方谱、四次方谱，根据谱特征来提取相应的特征参数。因在计算高阶谱时引入乘性噪声，低信噪比下的离散谱线特征不明显，识别性能较低。文献[4]和文献[5]均提出基于小波分析的信号识别算法，信号进行小波变换处理后，提取不同的信号特征，对信号进行识别。文献[6]提出一种基于独立成分分析与支持向量机(Independent Component Analysis-Support Vector Machines, ICA-SVM)的连续相位信号识别算法，针对不同种调制指数的CPM信号进行相关识别。文献[7]提出一种基于调制指数估计的CPM信号识别算法，根据CPM信号在不同调制指数下的不同循环谱特征进行识别。但是，以上算法需要较多的先验条件，在先验条件不足的情况下，识别性能不够理想。基于盲数字接收机的信号识别算法先通过普适数字接收机对各种信号进行同步解调，再对接收机输出信息进行特征提取，根据相应的特征进行信号识别，具有运算量小、识别特征明显等优势，普遍应用于非连续相位信号的识别。文献[8]提出一种基于数字接收机的信号识别算法，对输入信号进行同步解调，根据输出的同相支路与正交支路的特征信息对QPSK与BPSK进行识别，运算量小，在硬件方面容易实现。文献[9]提出一种基于接收机盲解调的高阶信号识别算法，在低信噪比下，通过统计同步环路输出的幅度信息对高阶信号进行识别，性能优于传统的星座图匹配算法。本文提出一种基于盲数字接收机与拟合优度检验的信号识别算法，用于识别连续相位信号SOQPSK与非连续相位信号{BPSK，QPSK，2FSK}，结合盲数字接收机识别算法与拟合优度检验算法，对盲数字接收机提取的特征进行识别，特征提取模糊时，仍可以根据分布距离远近对信号进行分类，提升了低信噪比下的识别率。

1 信号模型

为了识别SOQPSK与非连续相位信号{BPSK，QPSK，2FSK}，本文提出一种基于盲数字接收机与拟合优度的信号识别算法，其通用信号模型为：

(1)

式中，A为信号的幅值常数，fc为信号的中心频率，φ(t)为信号的相位变换函数，φ0为信号初始相位，n0(t)为服从N(0,σ2)的高斯白噪声。对于SOQPSK信号而言，受基带数据的影响，相位信息φ(t)产生变化，通过信息预编码与相位成型后，φ(t)呈现相位连续特性。PSK通过基带码元来控制相位变化，根据当前码元信息不同，φ(t)表现出不同的值。2FSK的中心频率fc存在2个频点fc1,fc2，通过基带码元使得中心频率在fc1,fc2之间跳变。

1.1 连续相位信号SOQPSK信号模型

本文研究的SOQPSK信号采用SOQPSK-MIL类信号，与BPSK，QPSK等相位调制信号的不同之处在于SOQPSK的相位变化是有斜率的，每个符号内的相位变化都是关于时间的函数[1]。另外，SOQPSK信号与其它CPM信号也有不同之处，SOQPSK信号在一个符号内的相位变化为±π/2或者不变，其信号模型表示为：

(2)

(3)

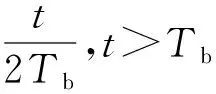
1.2 非连续相位信号模型

PSK调制信号通过基带码元来控制相位的变化，其载波振幅和频率不发生变化。在PSK信号模型中，式(1)中的φ(t)代表受基带信息影响变化的相位信息，BPSK有2个相位变化，QPSK有4个相位变化，展开式(1)后得到：

sPSK(t)=bi(t)cos(2πfct+φ0)-bq(t)sin(2πfct+φ0)

(4)

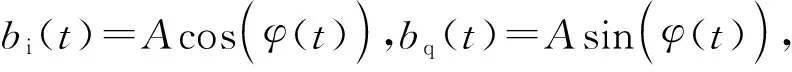
2FSK调制信号通过改变码元来改变信号频率，其数学模型如下：

s2FKS(t)=s1(t)cos(2πfc1t+φ0)+s2(t)cos(2πfc2t+φ0)

(5)

式中，s1(t)为单极性基带信号，s2(t)为s1(t)的反向信号，通过基带码元的控制使得频率在fc1，fc2之间跳变，相位呈现非连续特性。

2 基于盲数字接收机与拟合优度的信号识别方案

针对SOQPSK与非连续相位信号{BPSK，QPSK，2FSK}的识别，本文设计了一种基于盲数字接收机与拟合优度检验的信号识别方案。以盲数字接收机中的锁相环为主体，通过增加锁相环环路带宽和扩大环路跟踪范围等方式，设计具有较高普适性的盲数字接收机。首先，接收机对所有信号进行同步跟踪，提取信号同相支路、正交支路与频率跟踪信息特征，对信号同相支路信息的概率分布展开研究，研究发现，可以根据分布距离对信号进行粗分类；然后，采用拟合优度检验算法计算信号同相支路信息分布与目标分布的距离，将信号集分为{SOQPSK，2FSK}，{BPSK，QPSK}；最后，针对{SOQPSK，2FSK}信号集，通过统计锁相环输出的跟踪频率特征进行识别；针对{BSPK，QPSK}信号集，通过统计同相支路与正交支路相同符号数的数量进行识别。

2.1 基于盲数字接收机的信号特征提取

传统的连续相位信号与非连续相位信号识别算法中，通常采用直接提取信号特征的方式，受噪声的影响，识别性能波动较大。为了避免这一问题，本文采用盲数字接收机对信号进行特征提取。首先，运用快速傅里叶变换，粗估计信号载频与信号带宽；然后，在参数粗估计的先验条件下，运用锁相环实现信号特征提取。

在不考虑噪声情况下，输入锁相环的PSK信号分别与本地振荡信号cos(2πfNCOt+φNCO)，sin(2πfNCOt+φNCO)相乘，其中fNCO表示本地振荡信号频率，φNCO表示本地振荡信号初始相位。滤除高频分量后得到的同相支路与正交支路Si(t)，Sq(t)分别为：

(6)

(7)

式中，Δφ=φNCO-φ0表示本地振荡信号与输入信号的相位差。

在载波同步中采用的鉴相方程如下：

(8)

式中，sign[·]为符号函数，当Δφ≪π/4时，sin Δφ≈0，cos Δφ≈1，将式(6)，式(7)带入式(8)，得到鉴相方程为：

(9)

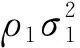
(10)

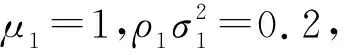
将SOQPSK信号与接收机中锁相环产生的本地振荡信号cos(2πfNCOt+φNCO)，sin(2πfNCOt+φNCO)相乘，并使用低通滤波器滤除高频分量，得到同相支路与正交支路信息。在环路接近稳定时，振荡器累计相角与振荡器输入相角接近相等，则振荡器的频率变化与信号频率变化接近相等，表示为2πfNCOt≈2πfct+φ(t,α)。因此，在不考虑噪声情况下，同相支路与正交支路为：

(11)

(12)

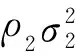
2FSK与SOQPSK相似，在环路稳定时，输出的同相支路为单极性信息且跟踪频率为2个频率点的跳变。能量归一化处理后，2FSK同相支路信息与SOQPSK同相支路信息服从近似相同的分布。综上所述，通过锁相环提取出{SOQPSK，2FSK}信号的同相支路信息服从高斯分布，该高斯分布的累积分布函数F2(x)表示为：

(13)

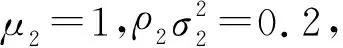
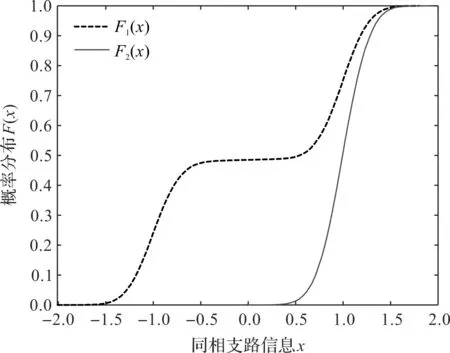
图1 同相支路信息累积分布

对比图1中的F1(x)，F2(x)可以发现，2个分布函数的差异比较大，说明可以通过分布距离对{BPSK，QPSK}信号集和{SOQPSK，2FSK}进行分类。拟合优度检验算法在度量分布距离方面具有较好的效果，故本文采用拟合优度算法进行信号的分类。

2.2 基于拟合优度的{SOQPSK，2FSK}和{BPSK，QPSK}信号集分类

2.1节中，对10 dB下的QPSK与SOQPSK的同相支路信息进行经验分布拟合，得到这2类信号的同相支路信息的累积分布函数Fm(x)(m=1,2)。将这2个累积分布作为目标分布，统计锁相环输出的同相支路信息的经验分布FL(x)，L表示观测的样本数量，计算FL(x)与目标分布Fm(x)(m=1,2)的距离，根据该距离进行信号的分类。本文采用AD检验方式计算分布距离[10]，其表示方式如下：

(14)

根据文献[11]中关于AD检验的理论推导，式(14)可简化为：

(15)

式中，zi=Fm(xi)(m=1,2)，xi表示当前第i个观测样本。

将4种信号{SOQPSK，BPSK，QPSK，2FSK}输入到盲数字接收机的锁相环中，得到的同相支路信息的经验分布FL(x)。运用拟合优度检验算法计算FL(x)与Fm(x)(m=1,2)的分布距离，得到特征量ALm(m=1,2)。4种信号的统计量ALm(m=1,2)随信噪比变化曲线如图2所示。

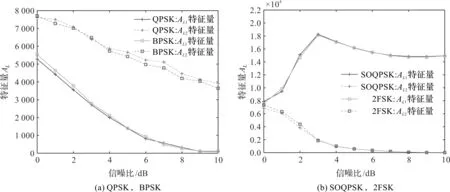
图2 统计量ALm(m=1,2)随信噪比变化情况

图2中，每种信号均有2个特征量AL1,AL2，分别表示经验分布FL(x)与2个目标分布F1(x),F2(x)的距离，分布距离越近，ALm(m=1,2)越小。通过寻找信号特征量ALm(m=1,2)对应的最小值m作为信号分类结果，

m=argminALm(m=1,2)

(16)

m=1时，说明该信号属于{BPSK，QPSK}；m=2时，说明该信号属于{SOQPSK，2FSK}。因此，可以将信号{SOQPSK，BPSK，QPSK，2FSK}信号分成2大类，分别为{BPSK，QPSK}和{SOQPSK，2FSK}。

2.3 基于频率跟踪的SOQPSK，2FSK信号识别

2FSK作为一种频移键控信号，频率在2个点之间跳变，而SOQPSK信号本身的频率变化受φ(t,α)相位函数的影响，在2个频率跳变的基础上，还增加了一种维持频率不变的状态，2种信号的频率跟踪曲线如图3所示。

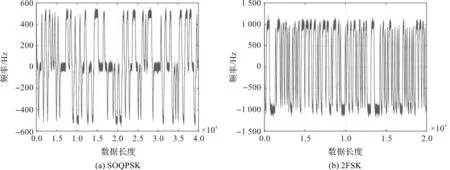
图3 SOQPSK和2FSK信号的频率跟踪曲线

符号速率为2 000 Baud，采样频率为400 kHz，码元长度N为200时，过零点数N0如图4所示。从图4可以看出，SOQPSK和2FSK信号的过零点数N0的曲线走势区分度大，所以，在采样频率为fs，码速率为R，码元长度为N，阈值系数为α时，选取T1=αNfs/R作为识别阈值，对{SOQPSK，2FSK}信号进行识别。选取不同的阈值系数α进行识别性能测试，α分别为0.035，0.045，0.055时，{SOQPSK，2FSK}信号的平均识别率随信噪比变化曲线如图5所示。从图5可以看出，α=0.045时的识别性能最好，因此取α=0.045时的T1作为判决阈值，当N0>T1时，判为SOQPSK信号，反之则为2FSK信号。

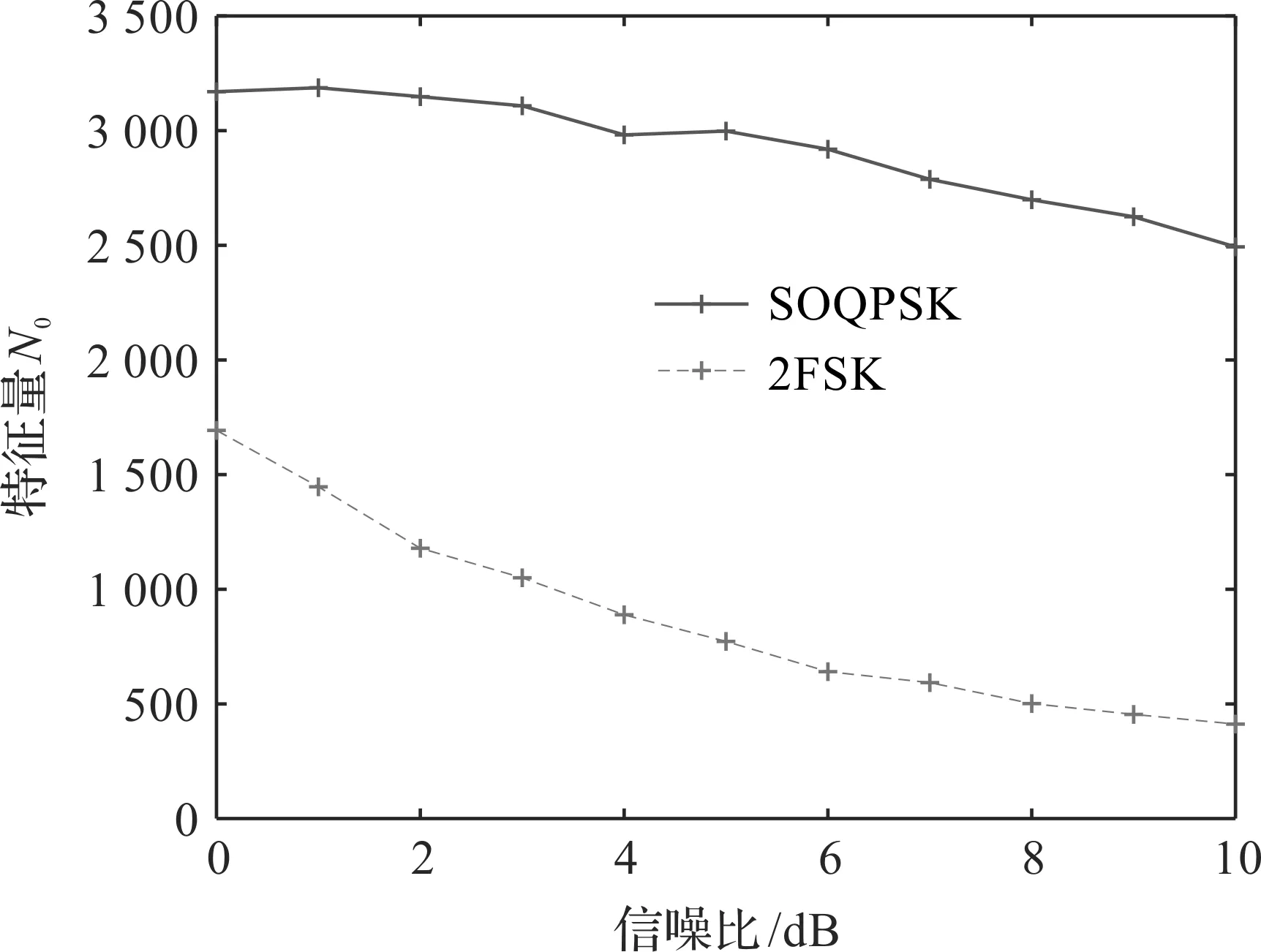
图4 特征量N0随信噪比变化曲线

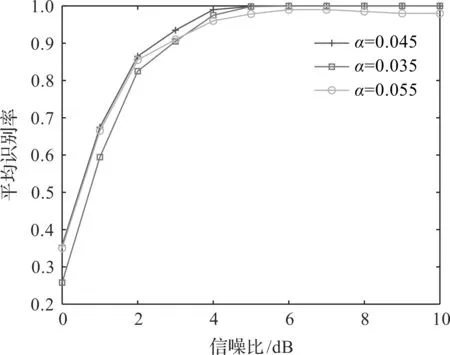
图5 不同α下，{SOQPSK，2FSK}平均识别率

2.4 基于同相支路与正交支路相同符号数的BPSK，QPSK信号识别

对于{BPSK，QPSK}信号，采用同相支路与正交支路的相同符号数E进行识别[8]，在码元长度N=200时，{BPSK，QPSK}信号的特征参数E如图6所示。从图6可以看出，随着信噪比的高，{BPSK，QPSK}信号的特征量E区分度增大，所以，在码元长度为N，阈值系数为β时，选取T2=βN作为识别阈值，对{BPSK，QPSK}信号进行识别。选取不同的阈值系数β进行识别性能测试，β分别为0.55，0.60，0.65时，{BPSK，QPSK}信号的平均识别率随信噪比变化曲线如图7所示。从图7可以看出，β=0.6时的识别性能最好，因此取β=0.6时的T2作为判决阈值，当E>T2时，判为BPSK信号，反之则为QPSK信号。

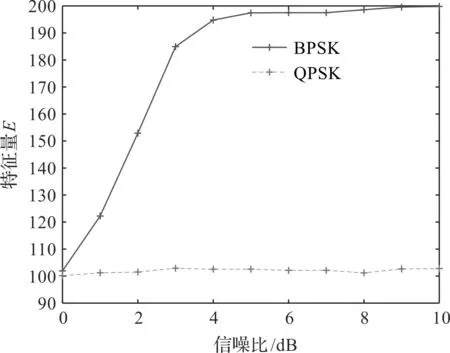
图6 特征量E随信噪比变化曲线

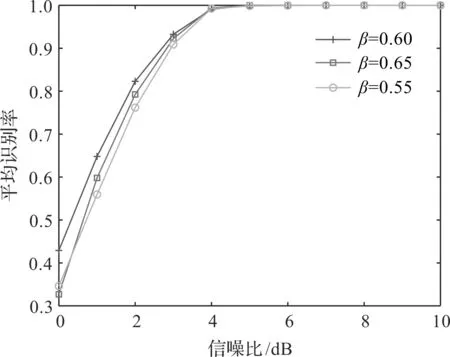
图7 不同β下，{BPSK，QPSK}平均识别率

2.5 基于盲数字接收机与拟合优度的识别算法流程

针对{SOQPSK，BPSK，QPSK，2FSK}信号集，本文提出的基于盲数字接收机与拟合优度的识别算法采用ALm，E，N0这3个特征量进行信号识别。先根据ALm将信号分为{SOQPSK，2FSK}与{BPSK，QPSK}，再针对特征量N0设计阈值T1进行SOQPSK和2FSK信号的识别，针对特征量E设计阈值T2进行BPSK和QPSK信号的识别。算法具体流程如图8所示。

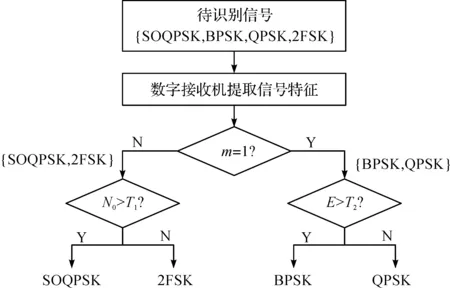
图8 基于盲数字接收机与拟合优度的识别算法流程图

3 仿真实验结果与分析

实验信号集{SOQPSK，BPSK，QSPK，2FSK}为中电科在实际卫星信道中采集的高信噪比信号，具体参数为：符号速率2 000 Baud，采样频率400 kHz，中心频率10 kHz，码元长度200。其中，SOQPSK采用SOQPSK-MIL形式，频率脉冲响应采用矩形脉冲，记忆长度为1，调制指数为0.5；2FSK信号的2个频率间隔为2 000 Hz。通过MATLAB2019对采集信号添加带限高斯噪声，并采用M2M4[12]信噪比估计算法进行信噪比评估。信噪比为0～10 dB时，分别采用本文提出的基于盲数字接收机与拟合优度的识别算法和文献[2]提出的基于瞬时幅度谱的识别算法对{SOQPSK，BPSK，QSPK，2FSK}信号进行识别仿真测试。每次测试进行1 000次蒙特卡洛实验，统计正确识别个数，计算得到对{SOQPSK，BPSK，QSPK，2FSK}信号的识别率如图9所示。

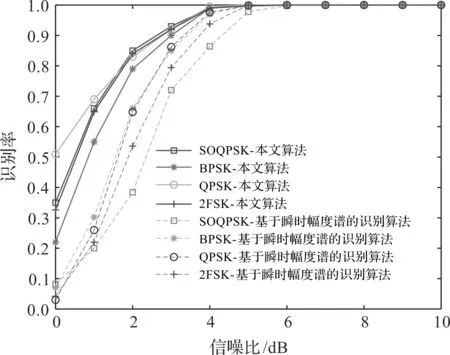
图9 不同信噪比下，2种算法的识别率

由图9可以看出，信噪比高于4 dB时，本文提出的基于盲数字接收机与拟合优度的识别算法对{SOQPSK，BPSK，QSPK，2FSK}信号的识别率均能达到90%以上，识别率优于文献[2]提出的基于瞬时幅度谱的调制识别算法。本文算法通过数字接收机中的锁相环来提取{SOQPSK，BPSK，QSPK，2FSK}的信号特征，锁相环本身具有一定的抗噪和抗频偏能力，另外，本文算法采用的拟合优度检验主要通过分布距离实现信号的粗分类，能更准确地反映信号的特征，因此，在低信噪比与具有频偏情况下，本文算法仍具有较好的识别效果。

4 结束语

为了识别连续相位信号SOQPSK与非连续相位信号{BPSK，QPSK，2FSK}，本文提出一种基于盲数字接收机与拟合优度的识别算法。研究了SOQPSK信号与PSK信号和2FSK信号的调制识别方式，并采用盲数字接收机识别算法与拟合优度检验算法对盲数字接收机提取的特征进行识别，有效识别了SOQPSK信号。算法简单易于实现，并具有一定的抗频偏优势。但是，本文算法中，增大环路带宽虽然增强了盲数字接收机的普适性，但也引入了一定的噪声增益，影响了数字接收机的稳定性，后续计划针对这个问题展开研究，进一步提升连续与非连续相位混合信号的识别性能。