小学高段学生符号意识测试问卷编制研究
2022-06-08巩子坤吴敏霞赵雨晴
巩子坤 吴敏霞 赵雨晴


【摘 要】符号意识是重要的数学核心素养之一。了解、测量学生的符号意识及其发展水平,有助于培养学生的符号意识,发展学生的数学核心素养。基于相关研究成果,编制了符合小学4~6年级学生生理及心理特质的符号意识测试问卷。通过多次大样本测试,结合探索性因素分析、验证性因素分析等结果,不断进行修订,最终形成的问卷包含符号理解、符号表示、符号运算、符号推理四个维度,共43道题。该问卷具有良好的信效度,可以作为评估4~6年级学生符号意识的有效工具。
【关键词】4~6年级学生;符号意识;问卷编制
一、引言
符号意识,是学习者将数学知识抽象成对应的数学符号的认知活动,是解决数学问题过程中表现出来的数学核心素养[1],其形成直接影响学生数学能力的发展。然而,目前在教学中没有专门的测试来检验学生的符号意识。四年级是从经验型思维向理论型思维转化的开始,是学生符号意识发展水平的关键节点[2-3]。本研究在已有研究的基础上,对符号意识的内涵进行了再认识,编制了符号意识测试问卷,为探明小学4~6年级学生的符号意识及其发展水平提供了基本工具。
二、问卷编制与实施
(一)符号意识内涵解读
我国对符号意识的研究晚于西方。以Abraham Arcavi[4]为代表的研究成果为国内进行符号意识研究奠定了基础。《义务教育数学课程标准(2022年版)》中指出符号意识主要是指能够感悟符号的数学功能。知道符号表达的现实意义;能够初步运用符号表示数量、关系和 一般规律;知道用符号表达的运算规律和推理结论具有一般性;初步体会符号的使用是数学表达和数学思考的重要形式。史宁中教授从行为的角度对课标进行了解读:理解符号意义和运用符号进行表达,通过符号操作得到一般性结论,强调学生学习数学符号的观念对数学发展的重要性。[5]李艳琴和宋乃庆认为,符号意识是指学生在表示数学概念、数学关系等符号的感受、体会、认识、理解、运用等方面的反应。[6]基于学者们对符号意识的解读,将符号意识分为符号理解、符号表示、符号运算、符号推理四个维度。
(二)问卷理论结构构建
我们基于对符号意识维度的划分,确定符号意识问卷的理论结构。为更好地编制符号意识测试题目,结合4~6年级学生的学习内容,尝试对各维度给出操作性定义,如表1所示。
(三)问卷测试题目编制
在设计题目的过程中,征求一线教师关于小学4~6年级学生的认知水平及题目呈现形式等的建议,同时征求了数学教育专家和优秀的小学数学教研员的意见,不断地对问卷进行修订,初步形成了符号意识测试问卷一。
(四)样本选取与问卷回收
为保证符号意识问卷的信效度,选取了三个样本分别进行测试。后一次测试问卷是基于前一次测试的数据分析结果进行修订后得到的。
使用问卷一对样本一进行测试,该样本来自杭州市J区某学校学习层次有明显差别的五年级学生,共4人。回收问卷共4份,其中有效问卷为4份,有效率达100%。
使用问卷二对样本二进行测试,该样本来自杭州市X区某学校四、五、六年级学生,共490人。回收问卷共490份,其中有效问卷为386份,有效率达78.8%。
使用问卷三对样本三进行测试,该样本来自杭州市G区某学校四、五、六年级学生,共450人。回收问卷共450份,其中有效问卷为402份,有效率达89.3%。
(五)数据分析工具与方法
每道题正确记1分,错误记0分。先利用SPSS对样本一数据进行统计分析,借助访谈了解学生对题目的理解情况,根据反馈修订问卷;再利用SPSS对样本二数据进行项目分析和探索性因素分析,以便得到问卷的主成分,调整问卷的理论结构及测试题目;最后利用AMOS对样本三数据进行验证性因素分析,确认问卷理论结构的合理性。
三、问卷预测与修订
(一)问卷预测
對样本一收集到的数据进行整理、录入。先结合访谈了解学生对题目存在困惑的地方,进而对4道题目进行调整与完善,形成问卷二。修改前后的题目如表2所示。
第一题属于“对运算符号的理解”维度,修改前的题目供学生思考的空间较小,部分学生会通过观察选择出现过相同的数的条件,而不是在理解算式的意义之后选择适用的条件。因此通过修改提供的条件,使得提供的条件中多次出现相同的数来改变这一情况。
第二题属于“抽象运算”维度,难度较大,因此在题目后给予一定的提示,但“k+2k=3×k=3k”连等的算式不利于学生对“数字乘字母”这种形式的理解。因此将提示改为“z+z+z=3×z”,指明“3×z,可以表示为3z”,并通过举例加深学生的理解。
第三题属于“合情推理”维度,由于“*”与乘号较像,将“*”改为“⊙”。
第四题也属于“合情推理”维度,该题以坐标的形式出现,超出了学生的认知范围,因此改为与该维度其他题目形式接近的题目。
(二)项目分析
对样本二收集到的数据进行项目分析。先用临界比率法删除不具有高低分组显著性差异的题目。再用题总相关法对各题得分与总得分之间进行相关分析,意在删除与总得分相关系数不显著的题目。经过项目分析,问卷二无删题,仍有46道题目。
(三)探索性因素分析
基于项目分析,对样本二数据进行探索性因素分析。KMO值为0.907,Bartlett球形度检验相关性显著(p<0.01),表明样本二数据很适合做因子分析。因此,使用主成分分析法和最大方差旋转法确定问卷的因子数和题目。经探索性因素分析,主成分与符号意识问卷的理论结构一致,删除1(1)、2(1)、2(2)、4(1)、4(2)、8(2)、9(1)共7道题。为更好地反映测试内容,需使各维度题目在3道或以上,故根据分析结果增加整数、分数维度的同质性题目各2道。1B464F7B-5FE0-4E50-B08C-3B7275142D42
如“对分数意义的理解”维度,删除了题目“一根绳子长2米,将它平均分成3段,每段占全长的 ,每段长 米”,增加了题目“一根绳子长3米,剪去2米,剪去的占全长的 ,剩余的占全长的 ”。这保证了分数测试维度题目的同质性。
修订后形成最终的测试问卷三,包含43道题,详见附录。
四、问卷检验与确定
(一)验证性因素分析
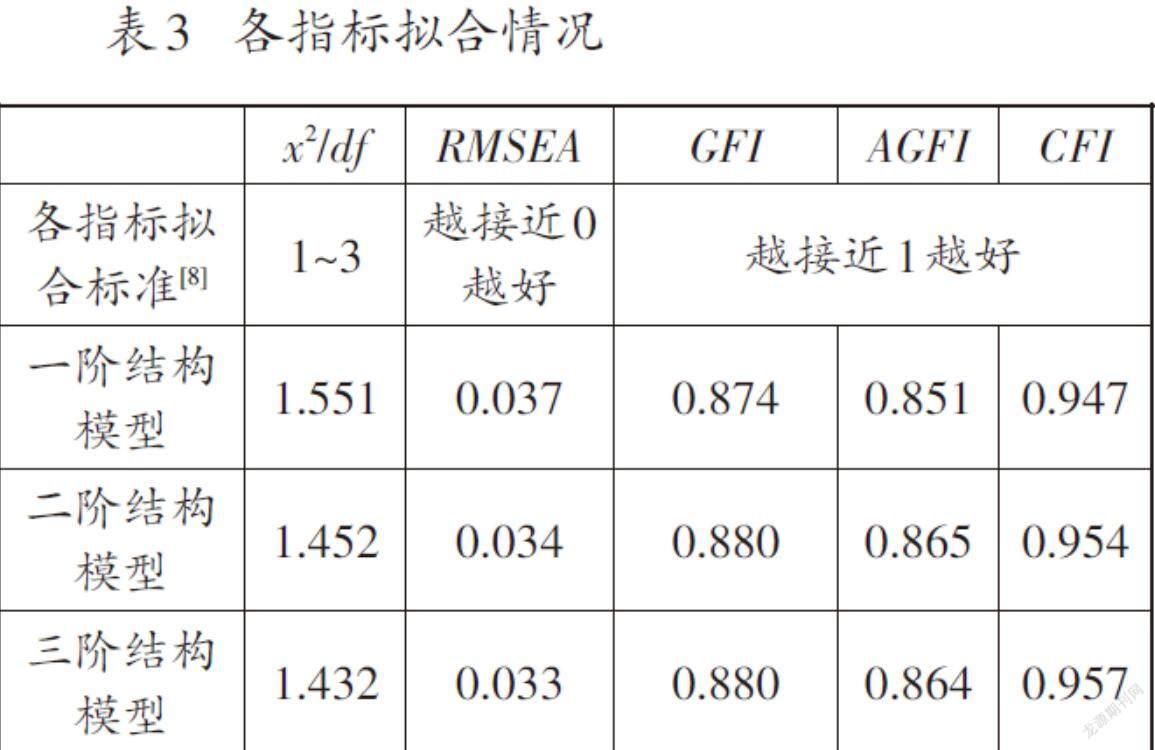
对样本三收集的数据进行验证性因素分析,检验实际数据与理论模型的拟合程度。首先构建一阶两两相关模型,根据分析结果进行残差修正,在各指标基本达到模型适配标准后再构建二阶模型。同理构建三阶模型。三种模型的各拟合指标如表3所示。
从拟合结果来看,随着结构模型的不断改进,各指标拟合得越来越好,且符号意识三阶结构模型的拟合指标基本达到了检验标准。因此,实际数据与该模型的适配情况良好,该符号意识理论结构和题目编制是比较合理的。本研究设计的小学4~6年级学生符号意识测试问卷的结构模型如图1所示。
(二)问卷的信度和效度分析
1.信度分析
信度是效度的前提条件。采用Cronbachs α系数检验问卷的内部一致性,考察问卷的每个题目是否测试了相同的内容或特质。数据表明问卷具有很好的内部一致性(如表4)。
2.效度分析
效度是指测试工具或手段能够准确测出所需测量事物特质的程度。本研究主要分析问卷的内容效度和结构效度。
(1)内容效度
内容效度指的是测试题目对有关内容取样的适用性。在问卷形成后,邀请4位专家对问卷题目与其所属维度的相关性做出评价,即在“‘1表示完全无关、‘2表示有点相关、‘3表示较强相关、‘4表示完全相关”的四点量表上做出判定。依据评价标准(K*:0.40~0.59为一般,0.60~0.74为良好,0.74~1.00为优秀[7]),35道题为优秀,8道题为良好。进一步计算,结果显示S-CVI/UA为0.81,S-CVI/Ave为0.95。根据S-CVI/UA不低于0.80,S-CVI/Ave应达到0.90的标准[8],该符号意识问卷的内容效度较好(表5)。
(2)结构效度
结构效度指的是测试结果体现出来的某种结构与理论结构之间的一致性。从验证性因素分析的结果来看,RMSEA在0.08以下,CFI等在0.9以上,因此拟合的三阶模型是一个“好模型”[9],该符号意识问卷的结构效度达到要求。
五、讨论
本研究重在编制小学4~6年级学生的符号意识测试问卷。相较于团队已有的研究成果,即“小学一年级学生符号意识测试问卷”和“小学2~3年级学生符号意识测试问卷”,以及目前的研究成果,本问卷编制的进步之处主要体现在以下两个方面。
(一)问卷理论结构更完善
三份问卷一脉相承,均包含符号理解、符号表示、符号推理、符号运算四个维度。随着学生认知水平的提高及知识量的增加,本问卷对结构进行了完善。特别是针对符号理解维度,将学生对数字符号的理解细分为对整数、分数、小数意义的理解;对关系符号的理解细分为对比较关系、等于关系的理解,同时增设对运算符号的理解这一考察维度。在一定程度上,本次问卷考察内容更细致,理论结构更完善。
(二)问卷编制过程更严谨
前两份问卷选取的样本量较小,数据分析易出现误差。为减少这一误差,本次问卷编制过程中选取了大样本用于探索性因素分析,并选取大样本对最终问卷进行验证性因素分析及信效度检验。因此,本次问卷编制过程更严谨、分析方法更科学。
六、結论
本研究编制的“小学4~6年级学生符号意识测试问卷”理论结构更完善,编制过程更严谨,且具有较好的信效度。因此,本问卷可有效测试小学4~6年级学生的符号意识,也可为小学高段学生符号意识评价体系的形成及相关研究提供参考。
参考文献:
[1]朱立明,马云鹏.“数学符号意识”研究:内涵与维度[J].教育理论与实践,2015,35(32):6-8.
[2]郑君文,张恩华.数学学习论[M].南宁:广西教育出版社,1996:90.
[3]朱立明.义务教育阶段学生数学符号意识发展水平研究[D].长春:东北师范大学,2017.
[4]Abraham A.Symbol Sense:Informal sense-making in formal mathetics [J].For the learning of mathematics,1994:3.
[5]史宁中.义务教育数学课程标准(2011年版)解读[M].北京:北京师范大学出版社,2012:84-85.
[6]李艳琴,宋乃庆.小学低段数学符号意识的含义及其表现形式[J].课程·教材·教法,2016(3):92-97.
[7]荣泰生.AMOS与研究方法[M].重庆:重庆大学出版社,2009(3):128.
[8]史静琤,莫显昆,孙振球.量表编制中内容效度指数的应用[J].中南大学学报(医学版),2012,37(2):49-52.
[9]崔宝蕊,李健,王光明.初中生数学元认知水平调查问卷的设计与编制[J].数学教育学报,2018,27(3):45-51.
附录:问卷三
亲爱的同学:欢迎参加这个小测试。请你仔细看题目,按照要求认真回答。测试的结果只用来做研究,与你的数学成绩无关。1B464F7B-5FE0-4E50-B08C-3B7275142D42
1. 4500000000里有45个 。60000000000里有600个 。
2. 37200000里有3720个 。
3. 一根竹竿长8米,截去5米,截去的占全长的 ,剩余的占全长的 。
4. 一根绳子长3米,剪去2米,剪去的占全长的 ,剩余的占全长的 。
5. 3.673中的左边起第一个“3”表示3个 ,第二个“3”表示3个 。
6. 1.57里面有15个 ,7个 。
7. 填空。
(1)298+a > 305,a 是自然数,最小是 。
(2)435-b > 427,b 是自然数,最大是 。
(3)70×c > 258,c 是自然数,最小是 。
8. 填空。
(1)150-q = 90+12,那么q= 。
(2)16×4 = m÷10,那么m = 。
(3)216÷n= 3×8,那么n= 。
9. 請根据算式选择适当的条件,并提出用该算式解决的问题。
水果摊运来一批橘子、梨、香蕉,若干天后全部卖完。
① 橘子有70千克。② 香蕉比橘子多50千克。
③ 梨比橘子少50千克。④ 每千克橘子卖6元。
⑤ 每千克梨卖5元。⑥ 每千克香蕉卖5元。
⑦ 香蕉10天卖完。⑧ 梨10天卖完。
⑨ 橘子总共卖了420元。⑩ 梨总共卖了100元。
(1)列出算式“70×6-100=320”需要的条件是 ,你提出的问题是 。
(2)列出算式“420÷6+50=120”需要的条件是 ,你提出的问题是 。
(3)列出算式“(70-50)×5=100”需要的条件是 ,你提出的问题是 。
(4)列出算式“(70+50)÷10=12”需要的条件是 ,你提出的问题是 。
10. 在横线上填上含有字母的式子。
(1)动物园里有a只兔子,有b只狮子,老虎的只数比兔子、狮子的总和少2只,动物园里有老虎 只。
(2)李明的爸爸买了c个苹果,妈妈回来后吃了1个苹果,李明放学回来后吃了d个苹果,还剩下 个苹果。
(3)仓库里有一批水泥,运走了5车,每车e吨,还剩下f吨,这批水泥共有 吨。
(4)小妍去商店买了3盒彩笔,共用去g元。如果买一盒铅笔用的钱比买一盒彩笔的钱少h元,那么买一盒铅笔需要用 元。1B464F7B-5FE0-4E50-B08C-3B7275142D42
(5)小华有铅笔i支,小强有铅笔j支。小华、小强的铅笔总数是小刚的3倍,小刚有铅笔 支。
(6)亮亮有k个梨,比丽丽多p个梨。如果花花的梨是丽丽的4倍,那么花花有 个梨。
11. 在横线上填上适当的数。
(1)27+13 = 54-a,a = 。
(2)b+34 = 75-23,b = 。
(3)56-10 = 17+c,c = 。
(4)60-d= 16+34,d = 。
12. 在横线上填上适当的式子。
(知识小贴士:z+z+z=3×z,可以表示为3z;3z+4z=7z;5z-2z=3z)
(1)a+2b = 10b-c,a = 5b,c = 。
(2)3t+f = q-t, q = 8t, f = 。
(3)m-3r = 2r+n,m = 6r ,n = 。
(4)8k-i = j+k , j = 3k ,i = 。
13.已知:3 ⊙ 2 =(3+2)×(3-2),5 ⊙ 4 =(5+4)×(5-4),7 ⊙ 5 =(7+5)×(7-5),请用字母表示你发现的规律: 。
14.已知:3@4=3×5-4×2,6@8=6×5-8×2,
9@5=9×5-5×2 ,請用字母表示你发现的规律: 。
15. 已知: 8 △ 4 =(8+2)÷(4+1),7 △ 2 = (7+2)÷(2+1),4 △ 2 =(4+2)÷(2+1),请用字母表示你发现的规律: 。
16. 已知:(12-10)÷ 2 = 12÷2-10÷2 ,(18-12)÷ 3 = 18÷3-12÷3 ,(25-15)÷ 5 = 25÷5-15÷5 ,请用字母表示你发现的规律: 。
17. 规定两种新运算“◎”和“○”,◎表示两数之中取大数的运算,○表示两数之中取小数的运算。如3◎5=5,7○10=7。请你算出以下两个式子的结果。
(1)(9○12)+(28◎4)= 。
(2)(19◎6)-(5○32)= 。
18. 规定一种新运算“※”,a※b=a×a-b×b。请你算出以下两个式子的结果。
(1) 9※(4※3)= 。
(2)(8※7)※5 = 。
(1. 杭州师范大学经亨颐教育学院 311121
2. 杭州市余杭区良渚杭行路小学 311101
3.浙江省杭州长河中学 310053)1B464F7B-5FE0-4E50-B08C-3B7275142D42
