基于上下文与马尔科夫矩阵分解的流式推荐算法

纪淑娟,申彦博,王 振

(山东科技大学 计算机科学与工程学院，山东 青岛 266590)

近年来，用户所处上下文环境信息更加容易获得，基于上下文的推荐算法逐渐成为备受关注的研究课题。Lombardi等通过对上下文信息降维，对上下文信息进行预处理，使得预处理后的上下文信息可以运用在任意一个传统的推荐算法上[1]。Baltrunas等则是通过项目分解的方式，对上下文信息进行预处理，同样地，预处理后的上下文信息可以运用在任意一个传统的推荐算法上[2]。上述两个算法都是通过在传统的推荐算法中融入预处理后的上下文信息，从而获得满足用户偏好并契合上下文要求的推荐列表，但这类方法普遍存在时间成本高且推荐准确率低的问题。Karatzoglou等在协同过滤模型的基础上，提出了一种基于张量分解的上下文推荐算法，该算法通过多维度上下文信息和正则化来构建目标函数，并且采用迭代学习的措施得到最终结果[3]。Oku等引入一种上下文信息支持向量机的思想，该算法考虑多维空间中的支持向量，并找到分离超平面[4]。Kim等提出了一种并行张量分解算法，加速大型数据集的张量分解以支持上下文推荐[5]。Wu等利用回归树进行上下文特征选择，解决了上下文特性选择问题[6]。

自1998年Henzinger等首次提出数据流式处理方法以来[7]，数据流式处理逐渐成为热门研究领域，而推荐系统中的推荐算法是其中最热门的研究对象[8-9]。大量处理流式数据的算法被提出[10-11]，用以提高推荐系统的推荐性能。

为了使推荐系统具备处理流式数据的能力，一些推荐系统采用在线学习的方式，克服了推荐系统中算法模型必须实时更新的难题。其中，文献[12-14]在基于内存的推荐算法基础上，在推荐算法中融合解决增量更新的措施，由于此类增量更新方法主要采用相似度计算进行更新，其计算耗时与数量成正比，无法克服流式数据环境下无法实时更新的问题。

在动态矩阵分解算法中， Zhang等提出了基于矩阵过程的马尔科夫分解(Markovian factorization of matrix process, MFMP)的电影推荐算法，该算法将矩阵分解技术与马尔科夫相关知识相结合[15]。一方面， MFMP算法能够捕获数据集中的时间动态；另一方面，算法将输入数据转换为流式数据，能够更好地捕获时间动态下用户的兴趣爱好变化，从而在不同时间为用户进行相应推荐。

在真实推荐系统中，用户对项目进行评分时所处的上下文环境也会对用户的偏好产生影响，而且随着时间变更的不仅是用户和项目的隐特征向量，用户所处的上下文环境也会改变。为了表现出上下文环境对用户偏好的影响，本文在iMFMP(i Markovian factorization of matrix processes)算法[16]的基础上，在流式推荐算法中考虑上下文因素，将矩阵分解技术、马尔科夫过程以及动态变化的上下文环境融合在一起，提出了一种基于上下文的流式推荐算法。

1 相关理论

定义1信息熵表示信息随机变量的混乱程度。随机变量越混乱，信息熵越大。假设X是一个有限的离散随机变量，其概率分布为

P(X={xi})={p(xi)},i=1,2,…,n。

那么随机变量X的信息熵为

(1)

式中n为随机变量的总个数。

定义2条件熵表示在一定条件下随机变量分布的混乱程度。假设两个事件用随机变量X与Y表示，X={x1,x2,…,xn},Y={y1,y2,…,ym}，则在随机变量X发生的条件下，Y分布的混乱程度即条件熵为

(2)

定义3信息增益是一种权衡样本特征重要性的方法。假设某个状态下系统的信息熵为H(Y)，特征X给定条件下系统的条件熵为H(Y|X)，特征X对系统的信息增益为

G(Y|X)=H(Y)-H(Y|X)。

(3)

2 基于上下文的马尔科夫矩阵分解方法

在真实的推荐系统中，用户评分时所处的上下文环境、上下文类型、上下文变化以及时刻变化都会对用户产生影响。根据文献[17]对上下文信息的建模，上下文环境会影响用户对项目的偏好。在iMFMP算法[16]的基础上，本文将矩阵分解技术、马尔科夫矩阵分解相关知识以及动态变化的上下文环境融合在一起，提出了一种基于上下文的流式推荐算法(streaming recommendation algorithm based on context, C-SRA)。

2.1 基于信息增益的上下文信息与评分相关性分析方法

为了引出C-SRA算法，首先介绍一种基于信息增益的上下文信息与评分相关性分析方法。在推荐系统中，用户在对项目进行评分时所处的上下文环境往往是嘈杂的。为了从嘈杂的上下文环境中选取有价值的上下文信息，下面给出基于信息增益的上下文信息与评分相关性分析方法的步骤。

第一步，首先对数据进行统计与分析，统计不同评分下，上下文信息的分布情况。

第二步，根据公式(1)，计算数据集上相同评分上下文信息的信息熵。

第三步，根据公式(2)，计算相同评分上下文信息的条件熵。

第四步，根据公式(3)，计算该数据集所有上下文的信息增益值。

然后,根据信息增益值的大小去除无用的上下文信息，保留有价值的上下文信息，并将保留下来的上下文信息集合记作CA。

以上步骤通过计算各上下文信息增益，可以将数据集中无用的上下文信息剔除，从而得到与评分相关性大的上下文信息。其时间复杂度为O(r×c)，其中r是级别的数目，c是上下文信息的数目。

2.2 C-SRA算法

根据心理学上“积极情绪产生正面影响、消极情绪产生负面影响”以及Zheng等提出的两个时刻评分的相关性计算方法[17]，本节将两类上下文信息融入流式推荐算法之中，提出了基于上下文的流式推荐算法。

根据前面提出的基于信息增益的上下文信息与评分相关性分析方法，可以得到与评分相关性大的上下文信息集合。将心理学上“可以受人的主观意识影响的上下文信息”如人的情绪、心情等，记作主观上下文信息；将“客观存在于真实世界的上下文信息”如时间、地点等，记作客观上下文信息。下面将详细介绍如何将上下文信息有效地与流式推荐系统相结合，进一步提高推荐性能，算法模型如图1所示。

图1 C-SRA算法模型图

对于主观上下文信息，本文根据心理学上“积极的情绪会给用户带来正面的影响、消极的情绪会给用户带来负面的影响”这一认知，如果用户i在t时刻较(t-1)时刻情绪存在积极变化，则用户i对任意一个项目的评分在t时刻较(t-1)时刻会产生正相关变化；相反，如果用户i在t时刻较(t-1)时刻情绪存在消极变化，则用户i对任意一个项目的评分在t时刻较(t-1)时刻会产生负相关变化。本文通过计算情绪变化因子(pE)来判断情绪的积极变化(pE>0)和消极变化(pE<0)。

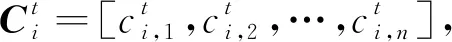
(4)

本文采用线性回归算法计算上述主观上下文信息对情绪变化因子的影响，并利用批量梯度下降(batch gradient decent, BGD)算法对权重系数w进行迭代训练。

情绪变化因子pE的损失函数如(5)式所示,然后利用(6)式对权重系数w进行批量梯度训练。

(5)

⋮

(6)

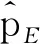
对于客观上下文信息，通过建模两个时刻上下文信息的相关性，可以计算两个时刻用户对项目偏好的相似性[17]。通过计算关联系数的方法，将客观上下文信息融入本文所提算法模型当中。

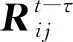
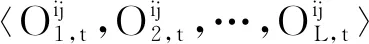
(7)

1)在时间t=0时，对于历史上第一个用户和项目的更新规则如下：

(8)

2)对于在(t-τ)时刻存在当前t时刻依然存在的用户和项目的更新规则如式(9)所示。

3)对于在t时刻新产生用户的更新规则如式(10)所示。

4)t时刻新产生项目的更新规则如式(11)所示。

5)最终的评分预测公式如式(12)所示。

(9)

(10)

(11)

(12)

(13)

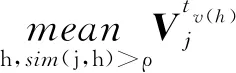
综合以上内容得到的C-SRA算法如下。

算法1C-SRA算法

输入：t时刻用户-项目评分矩阵Rt，正则化参数λ，特征矩阵训练学习率η，终止时间T，上下文信息集合CA，项目相似度阈值ρ，权重系数w,训练学习率δ。

用随机值初始化Ui和Vj

fort=0,t<=T,t+=τ

for (i,j)∈Rt

ift=0

else ift≤T

if用户i已经存在

最后，科学合理地安排英语阅读时间。要根据学生的平时英语阅读习惯，来有针对性地安排课外阅读的时间，并对其课外阅读学习进行指导，鼓励学生养成收集英语阅读材料的好习惯，提高学生英语阅读的自觉性，并给予学生足够的时间进行集体阅读。相比较而言可以适当地减少英语其他方面的作业布置时间。

if项目j已经存在

else if用户i是新用户

else if项目j是新项目

end if

end for

end for

经过分析，本算法时间复杂度为O(T×N×M)。

3 实验及结果分析

为了验证本文提出的基于上下文的流式推荐算法(C-SRA算法)的有效性，将C-SRA算法在LDOS-CoMoDa数据集上与其他现存算法进行对比实验。下面将对实验数据集、评价指标以及实验结果进行详细介绍。

3.1 数据集

为了充分论证C-SRA算法的有效性，本节实验选取LDOS-CoMoDa公开数据集进行实验。对数据集的介绍详见表1～2。

表1详细说明了LDOS-CoMoDa数据集的评分数、评分形式、用户数、物品数、物品类型以及上下文信息个数和物品特征数。表2是对LDOS-CoMoDa数据集中上下文的详细介绍。

表1 LDOS-CoMoDa数据集

表2 LDOS-CoMoDa数据集上下文

3.2 评价指标

为验证本文算法的有效性，选用均方根误差(root mean squared error, RMSE)、精确率(precision)以及召回率(recall)作为实验的评价指标，其中均方根误差用来评价C-SRA算法在评分预测方面的性能，精确率和召回率用来评价C-SRA算法在推荐方面的性能。均方根误差、精确率以及召回率的具体计算方法如下所示。

均方根误差(RMSE,式中简记为ERMS)用来衡量预测值与真实值之间的偏差，即

(14)

精确率表示用户看过的电影出现在TOP-N推荐列表中的数量占推荐列表长度的百分比，即

(15)

式中:LU表示给用户U的推荐列表集合；BU表示用户U在测试集评分过的项目集合。

召回率表示用户看过的电影出现在TOP-N推荐列表中的数量占用户所有看过电影数量的百分比,即

(16)

式中:LU表示给用户U的推荐列表集合；BU表示用户U在测试集评分过的项目集合。

3.3 数据预处理与分析

在对本文算法进行实验之前，首先根据基于信息增益的上下文与评分相关性分析方法对LDOS-CoMoDa数据集进行数据预处理与分析，得到LDOS-CoMoDa数据集上不同评分下各个上下文信息的统计结果。然后，计算LDOS-CoMoDa数据集上各上下文的信息熵与信息增益。保留信息增值大于0.002的上下文信息，然后将上下文信息分为主观上下文与客观上下文两类，具体的分类结果如表3所示。

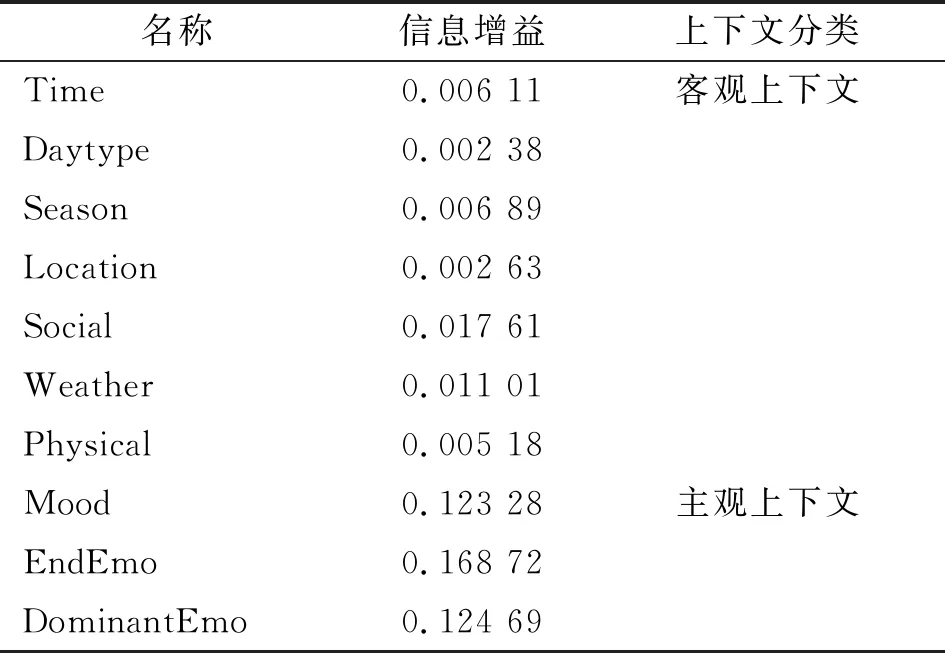
表3 上下文分类结果

通过表3可以发现Mood、EndEmo以及DominantEmo这3类上下文的信息增益值要明显大于其余7类上下文。将上述3类上下文统称为主观上下文，将剩余7类上下文统称为客观上下文。

本文假设用户的情绪波动在一段时间内是稳定的，由于LDOS-CoMoDa数据集整体时间跨度较小，所以不再对LDOS-CoMoDa数据集进行划分。在得到表3中3类主观上下文的基础上，采用线性回归梯度下降的方法在LDOS-CoMoDa数据集上全局静态计算每一个用户主观上下文的权重系数。权重系数训练的学习率取值为0.02，迭代次数为50 000次，然后以EndEmo权重系数为x坐标轴、DominantEmo权重系数为y坐标轴、Mood权重系数作为z坐标轴，根据最终训练结果构建三维坐标图，其结果如图2所示，其中每一个用户用一个☆表示。

图2 权重训练结果

由图2可以看出，LDOS-CoMoDa数据集上大多数用户的3个权重系数分布在0.25～0.5范围内。由此可知，对于大部分用户，3类主观上下文对用户评分的影响相差不大，并且大多数用户的情绪在整个时间线上是稳定的，这与本文关于用户情绪波动在一段时间内是稳定的这一假设一致。

3.4 实验设置

为充分验证C-SRA算法的有效性，将C-SRA算法在LDOS-CoMoDa数据集上进行2组对比实验。

第一组实验以RMSE作为评价指标，在LDOS-CoMoDa数据集上将C- SRA算法与经典的矩阵分解算法PMF、流式矩阵分解推荐算法MFMP、iMFMP和上下文推荐算法BiasTF-RT算法作比较，旨在验证C-SRA算法融合上下文的方法是否能够有效提高算法在评分预测方面的性能。

第二组实验在第一组实验的基础上，以精确率、召回率作为评价指标，在LDOS-CoMoDa数据集上将C-SRA算法与经典的矩阵分解算法PMF、流式矩阵分解推荐算法MFMP、iMFMP和上下文推荐算法BiasTF-RT算法作比较，旨在验证本文提出的C-SRA算法在LDOS-CoMoDa数据集上的推荐性能。同样地，两组实验均采用80%数据集作为训练集，20%数据集作为测试集，且学习率取值为0.02，迭代次数均为50 000次。

3.5 实验结果与分析

第一组实验对比结果如表4所示。

表4 LDOS-CoMoDa各算法RMSE对比

通过表4可以看出，C-SRA算法在LDOS-CoMoDa数据集上的RMSE值均小于其他算法，iMFMP算法次之。这一实验结果验证了C-SRA算法中数据预处理与参数训练的合理性，证实了算法融合上下文方法的有效性，证明了流式矩阵分解算法中融入上下文信息能够有效地提升推荐系统在评分预测方面的性能。并且从整体结果来看，在流式矩阵分解的基础上加入上下文的方法可以提高推荐系统的性能。

第二组实验结果如图3、表5所示。

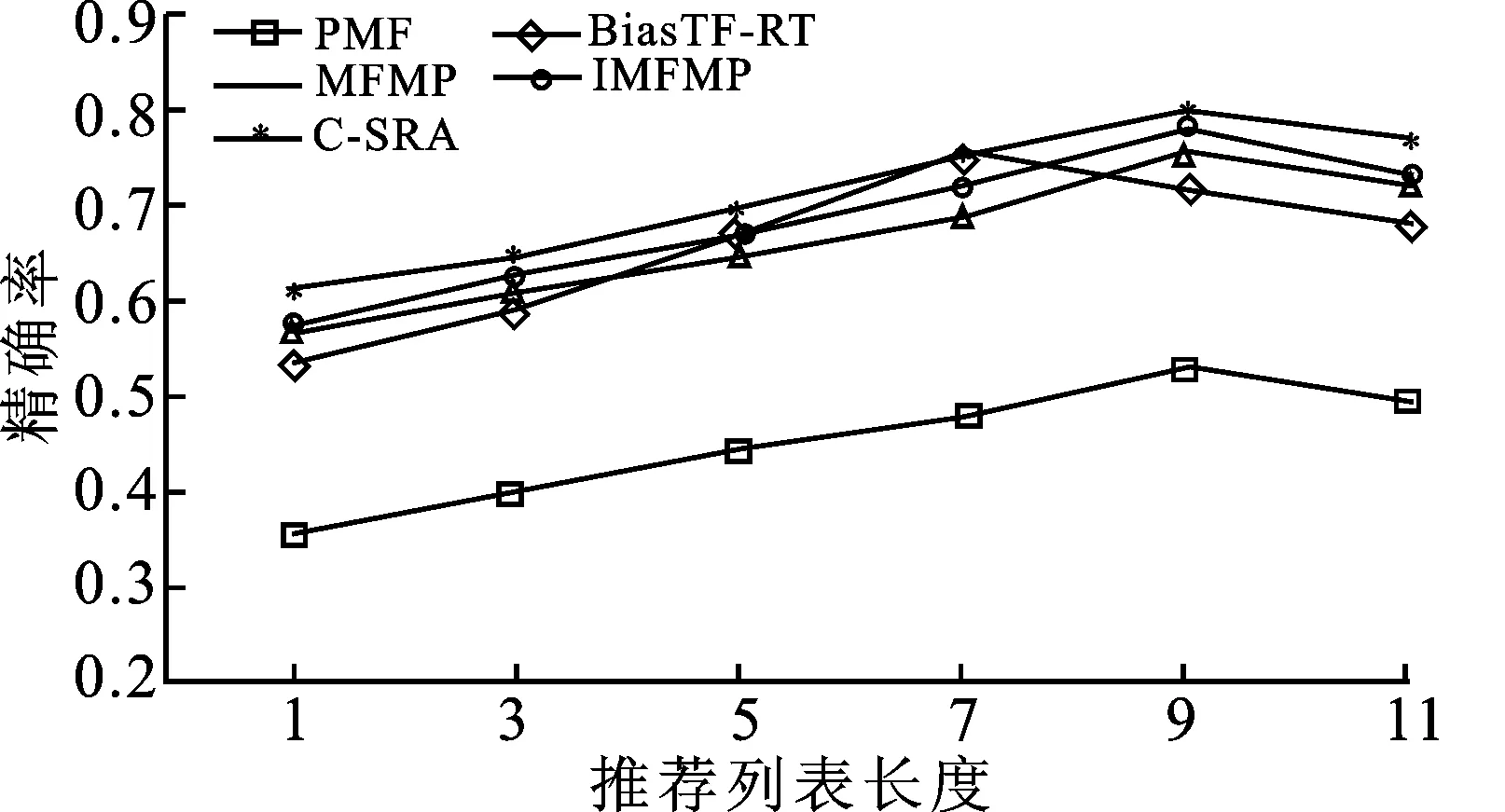
图3 LDOS-CoMoDa各算法精确率对比

表5 LDOS-CoMoDa各算法召回率对比

通过图3可知，本文提出的C-SRA算法在精确率上的整体性能均要优于PMF[19]、MFMP[15]以及BiasTF-RT[6]算法，并且C-SRA算法与iMFMP算法精确率均在推荐列表长度为9时达到最大值，证明了iMFMP算法处理新产生用户、项目的方法的有效性，以及C-SRA算法中对数据预处理与参数训练的合理性，证实了C-SRA算法融合上下文方法的有效性，流式矩阵分解算法中融入上下文信息能够有效地提升推荐系统的推荐精确率。PMF算法以及MFMP算法同样在推荐列表长度为9时精确率达到最大值，BiasTF-RT算法则是在推荐列表长度为7时精确率达到最大值。从整体走势来看，随着推荐列表长度的增加，算法推荐精确率整体呈现先上升后下降的趋势。

通过表5可以看出，本文提出的C-SRA算法在不同推荐列表长度上的召回率均要优于PMF、MFMP、iMFMP以及BiasTF-RT算法，并且iMFMP算法的整体召回率也均优于其余算法，再次证明了iMFMP算法处理新产生用户、项目的方法的有效性，以及C-SRA算法中对数据预处理与参数训练的合理性，证实了C-SRA算法融合上下文方法的有效性，证明了流式矩阵分解算法中融入上下文信息能够有效地提升推荐系统的推荐召回率。从整体来看，召回率与推荐列表长度正相关。

对比实验证明，在流式推荐算法的基础上考虑上下文信息可以提升算法的评分预测性能和推荐性能，从而证明了本文提出的基于信息增益的上下文与评分相关性分析方法的有效性。

4 总结与展望

本文提出了基于上下文的流式推荐算法，并提出了一种基于信息增益的上下文信息与评分相关性分析方法，详细介绍了如何将分类的上下文有效融合到流式推荐算法之中。通过C-SRA算法在LDOS-CoMoDa数据集上的两组实验，验证了本文提出的C-SRA算法无论是评分预测性能还是推荐性能均要优于其他算法。

然而，文中给出的算法模型并没有考虑潜在特征的突然变化，当数据集中存在明显的此类现象时，应考虑比依赖高斯分布更一般的模型。例如，可以采用类似于贝叶斯的方法对现有模型进行高参数扩充。这种模型下的推理通常在所有模型参数设置上表现出平均效果，并且有利于避免过度设置。

在算法模型中，本文假设用户的情绪波动是稳定的，因此对主观上下文的权重训练是基于全局数据进行的静态训练。如何对主观上下文的权重进行实时在线训练将是接下来要解决的问题。并且，面对未来规模更加庞大的数据量，用户对推荐系统的实时性要求将更加严格，如何在准确推荐的同时降低算法的时间复杂度将成为下一步研究的重点。