考虑分时电价的微电网储能容量优化配置

阚圣钧 ,魏少雄 ,赵继钢 ,张继红

(1.内蒙古科技大学信息工程学院,内蒙古自治区 包头市 014000;2.中国电建集团北京勘测设计研究院有限公司,北京市 朝阳区 100020)

0 引言

随着我国“双碳”目标的提出,光伏、风电等可再生能源的利用成为了国内外学者的重点研究方向[1-3]。然而,由于可再生能源具有随机性与波动性,大规模接入会对电网造成冲击,影响电网安全稳定运行[4]。将分布式可再生能源、储能、负荷有机结合的微电网技术则可以有效解决这一问题[5]。其中,储能系统因其具有能量密度高、充放电灵活、反应迅速等优点成为了决定微电网性能的关键部件之一,其容量配置和合理性将对微电网的整体性能和经济性造成极大影响[6-8]。因此,研究储能容量优化配置方法对微电网规划运行具有重要意义。

目前,国内外学者对储能容量优化配置方法进行了大量研究。文献[9]提出了考虑光伏消纳的光伏电站储能容量优化方法,通过对该电站的光伏出力与厂用负荷数据进行分析,降低了弃光率,提高了经济性。文献[10]提出了一种考虑锂电池和超级电容容量的混合储能系统容量优化配置方法,确定了系统年综合成本最小的滤波阶数和对应的储能配置方案。文献[11]提出一种氢气和蓄电池混合储能系统的风/光/储并网型微电网结构,以总净现值成本最小为目标函数,考虑了可再生能源利用率和负荷缺失率,对微电网进行了容量优化配置研究,证明了该方法的经济性与实用性。文献[12]在考虑储能系统能耗的前提下建立了容量配置模型,提出了一系列储能调度策略,研究了不同策略下容量优化配置的效果。文献[13]在考虑风速和负荷增长率的同时,对风力 柴油混合动力系统中储能容量配置进行优化,证明了在项目年限、备用容量、柴油机最小功率变化时,储能最优容量变化较小。文献[14]从电池储能在电力负荷调度中的应用角度,设置了一种非对称性稳定线性成本函数,研究了电池容量、单位电池成本与经济成本及收益间的关系,详细论证了随着未来电池成本降低,储能系统将极大降低电网运行成本。文献[15]以光伏出力预测为基础,对比了分时电价下单光、单储、光储3种情况下容量配置对系统成本影响,但并未考虑分时电价下调度策略对运行成本的影响。

本文在以往研究的基础上,充分考虑了分时电价对储能系统调度的影响,以并网型光储微电网为研究对象,以系统经济性最高为优化目标,以某社区微电网光伏出力和负荷功率为计算数据,对微电网的储能容量进行优化,分析考虑分时电价前后容量配置对微电网经济性的影响。

1 系统结构

本文所构建的微电网系统结构如图1所示,图中PCC为微电网的并网点(point of common coupling)。

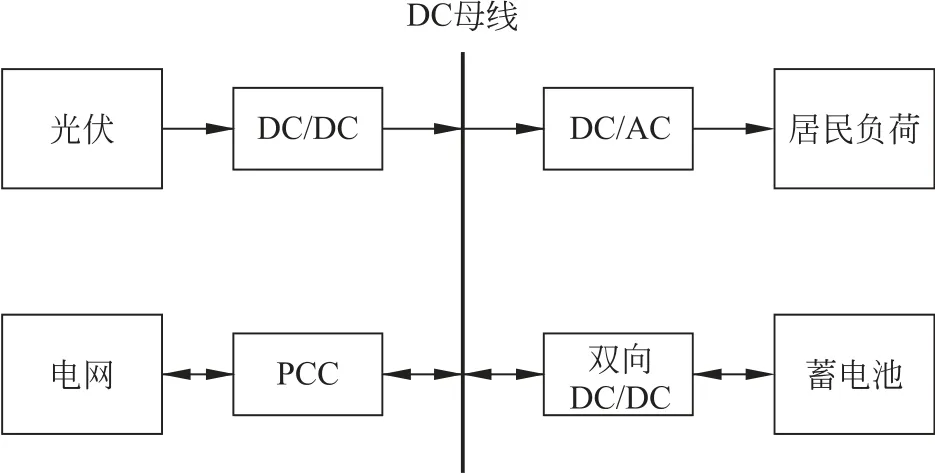
图1 微电网系统结构Fig.1 Structure of microgrid system

该系统以光伏阵列作为居民主要供电设备,蓄电池在平抑光伏波动的同时,可在能力范围内响应电网调度,帮助电网削峰填谷。日间光伏发电量高时,蓄电池存储多余电能,夜间释放电能支撑居民负荷。由微电网调度策略决定是否向大电网购买或返送电能。

2 优化配置模型

2.1 容量优化目标

本文以微电网初建成本、运维成本及购售电成本最低为优化目标,其数学模型为:

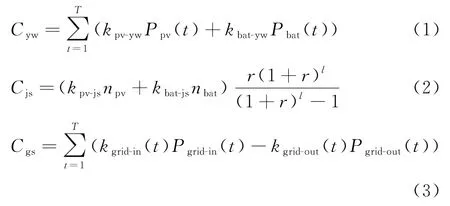
式中:Cyw为运维成本,元;kpv-yw、kbat-yw分别为光伏和蓄电池的度电运维系数,元/(kW·h);Ppv(t)、Pbat(t)分别为光伏和蓄电池的实际运行功率,kW;Cjs为建设成本,元;kpv-js、kbat-js分别为光伏和蓄电池的设备初建成本,元/台;npv、nbat分别为光伏和蓄电池的工程年限内使用设备数;r 为通货膨胀率,%;l 为工程设计年限;Cgs为购售电成本,元;kgrid-in、kgrid-out分别为购电价格、售电价格,元/(kW·h);Pgrid-in、Pgrid-out分别为购电功率、售电功率,kW。

2.2 约束条件

(1) 装置数量约束。

对装置的配置数量设置上下限,其大小一般取决于用户需求、已有装置数、空间地理条件限制等。

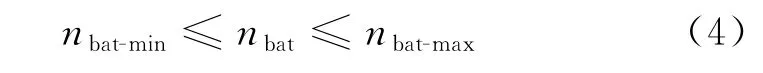
式中:nbat为蓄电池的配置数量;nbat-min、nbat-max分别为蓄电池的数量配置上下限。

(2) 功率平衡约束。

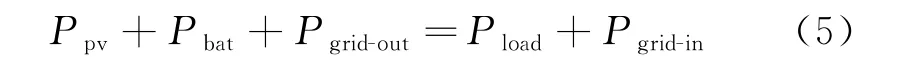
式中Pload为负荷的功率,kW。

(3) 电池运行约束。

电池荷电状态由上一时刻荷电状态及充放电功率决定,其表达式为

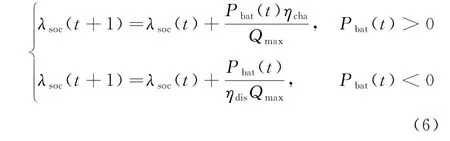
蓄电池功率上下限为

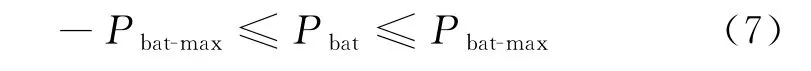
荷电状态上下限为

式中:λsoc为荷电状态;Qmax为电池最大容量,kW·h;ηcha、ηdis分别为蓄电池充放电效率,%。

2.3 优化算法

本文采用粒子群(particle swarm optimization,PSO)优化算法对模型进行求解。该算法是一种模仿鸟群行为的进化算法,与其他优化算法相比,粒子群算法具有经典、简单、可靠、高效等特点[16]。首先,对群落的粒子个数、维数、位置、速度等进行初始化;然后,根据输入数据及各个约束条件完成系统全年仿真计算各粒子当前适应度,更新个体最优值与群体最优值[17];在达到迭代次数或者终止条件时结束优化,输出最佳的粒子位置和适应度。

3 考虑分时电价的调度策略

3.1 电网分时电价

根据配电网中负荷情况可将用电情况分为平谷、低谷、高峰,依据不同用电情况设置分时电价有助于加强电力系统需求侧响应,帮助电网削峰填谷[18]。表1为某地24 h内不同时段的购售电价。

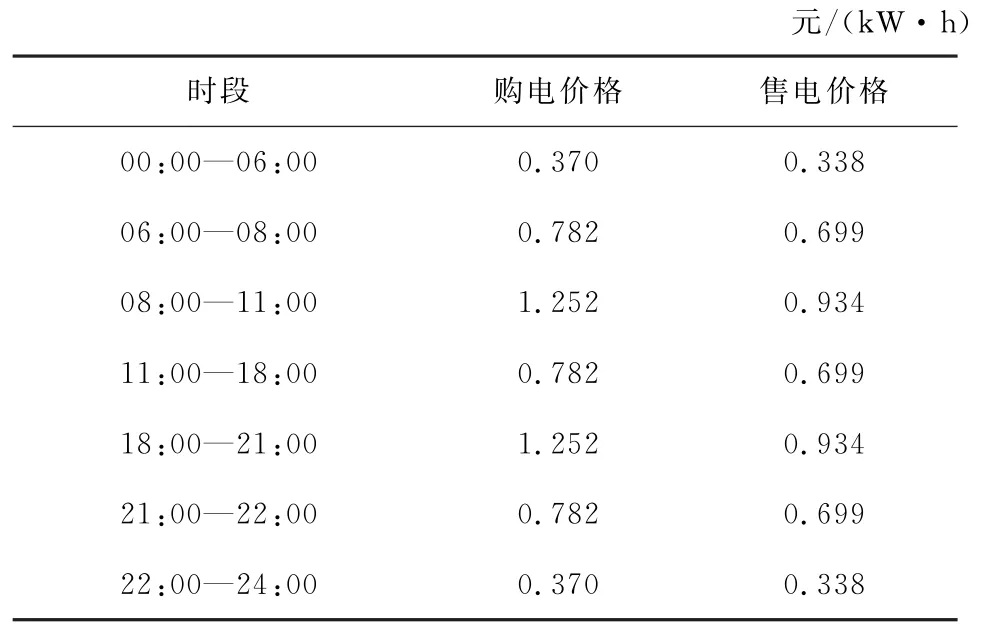
表1 某地电网分时电价Table 1 Time-of-use electricity price of local power grid

3.2 调度策略

在研究优化配置问题时,除确定优化目标函数、优化模型、约束条件外,还需确定调度策略,本文所用调度策略如图2所示。

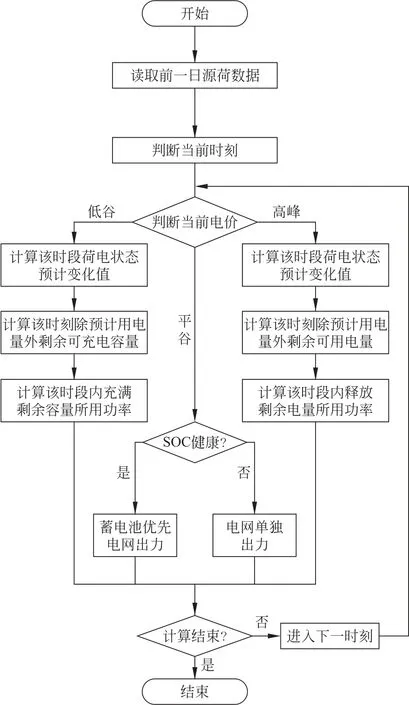
图2 调度策略Fig.2 Scheduling policy

在传统的固定逻辑调度策略中,通常制定装置出力优先级,光伏出力最高,蓄电池用于平抑光伏与负荷功率差,不足部分由电网补充。本文采用的考虑分时电价的调度策略在以往的基础上做出一定改变,首先依照前一日光伏负荷数据预测当前电价时段的电池充放电预估值,依照此预估值在电价低谷时增加电池充电功率,在电价高峰时增加放电功率。

4 算例分析

4.1 算例数据

本文采用某地光 荷历史数据作为算例,进行7日内容量优化仿真,其中光伏出力及负荷曲线如图3所示。优化模型的计算步长为1 h,共168组数据。光照强度平均值为349.08 W/m2,光伏峰值总功率为1 000 kW,光伏平均日发电量约为8.38 MW·h,平均日用电量约为14.01 MW·h,通过上述优化模型对微电网系统的储能容量配置进行优化计算。

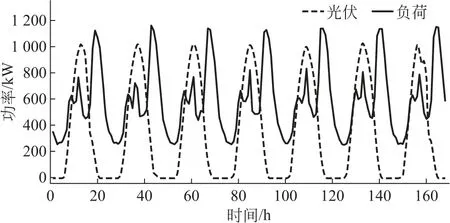
图3 光伏出力及负荷曲线Fig.3 Photovoltaic power and load curve

储能单元参数如表2所示,通货膨胀率为5%,项目规划年限20年。

表2 储能设备参数Table 2 Parameters of energy storage device

4.2 优化结果

根据前文所述优化目标和约束条件,以本节源荷数据为基础,利用PSO 算法对微电网中储能系统容量进行优化配置,得到考虑分时电价前后的优化结果对比如表3所示。

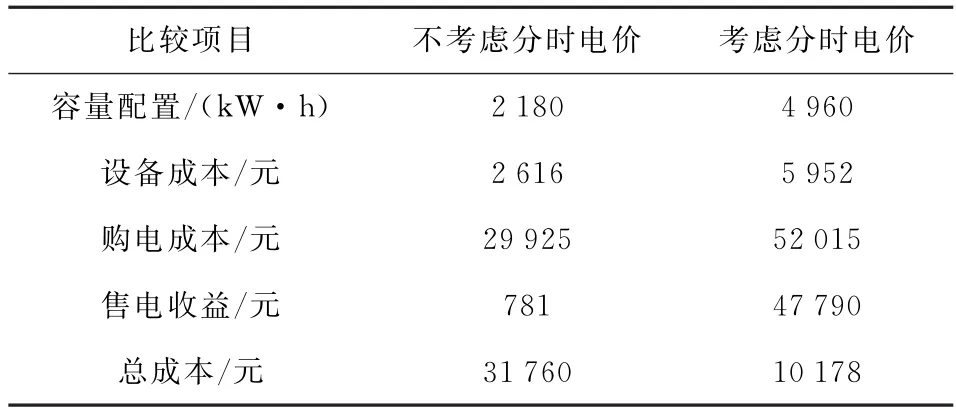
表3 优化配置结果Table 3 Results of optimized configuration

按照上述2种配置结果对微电网进行7 日仿真,考虑分时电价前后的运行曲线如图4—5所示。

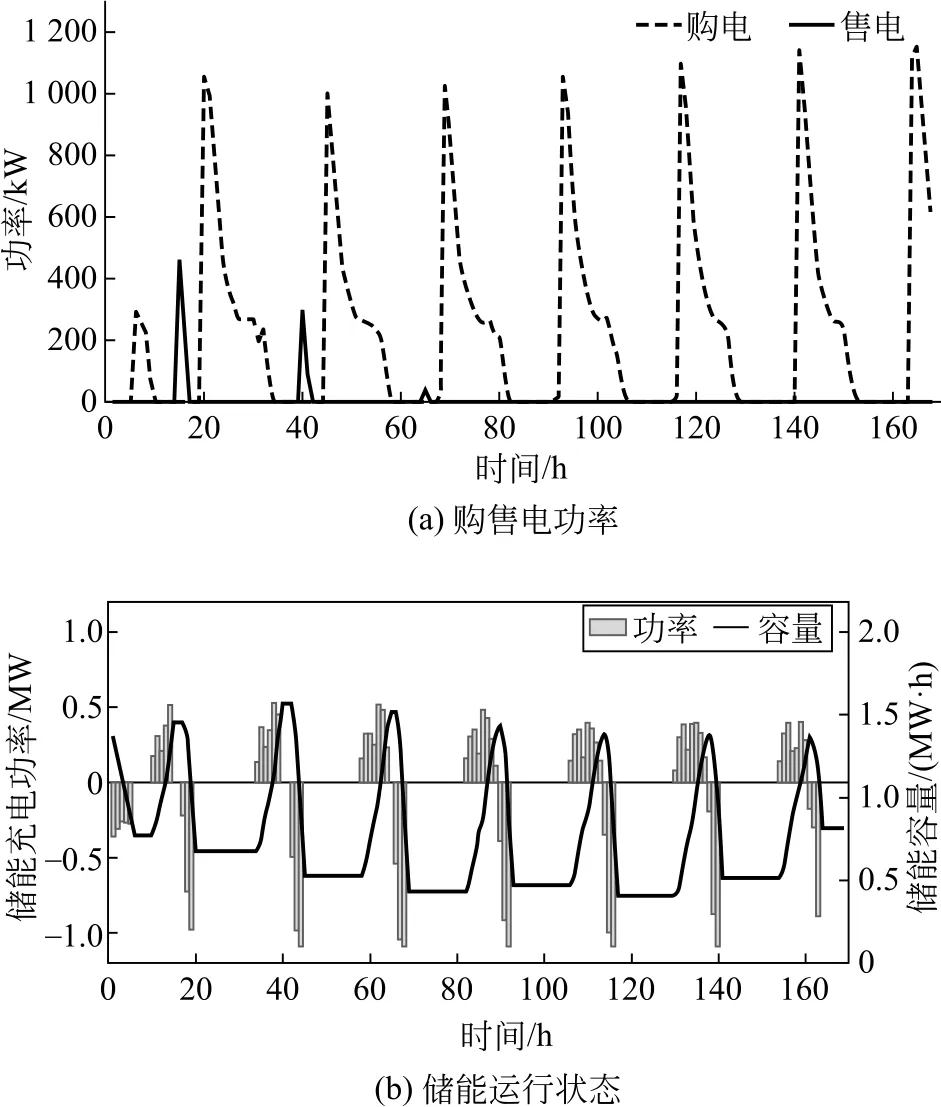
图4 不考虑分时电价的购售电功率和储能运行状态Fig.4 Purchase and sale of electricity power and energy storage operation state without considerating time-of-use electricity price

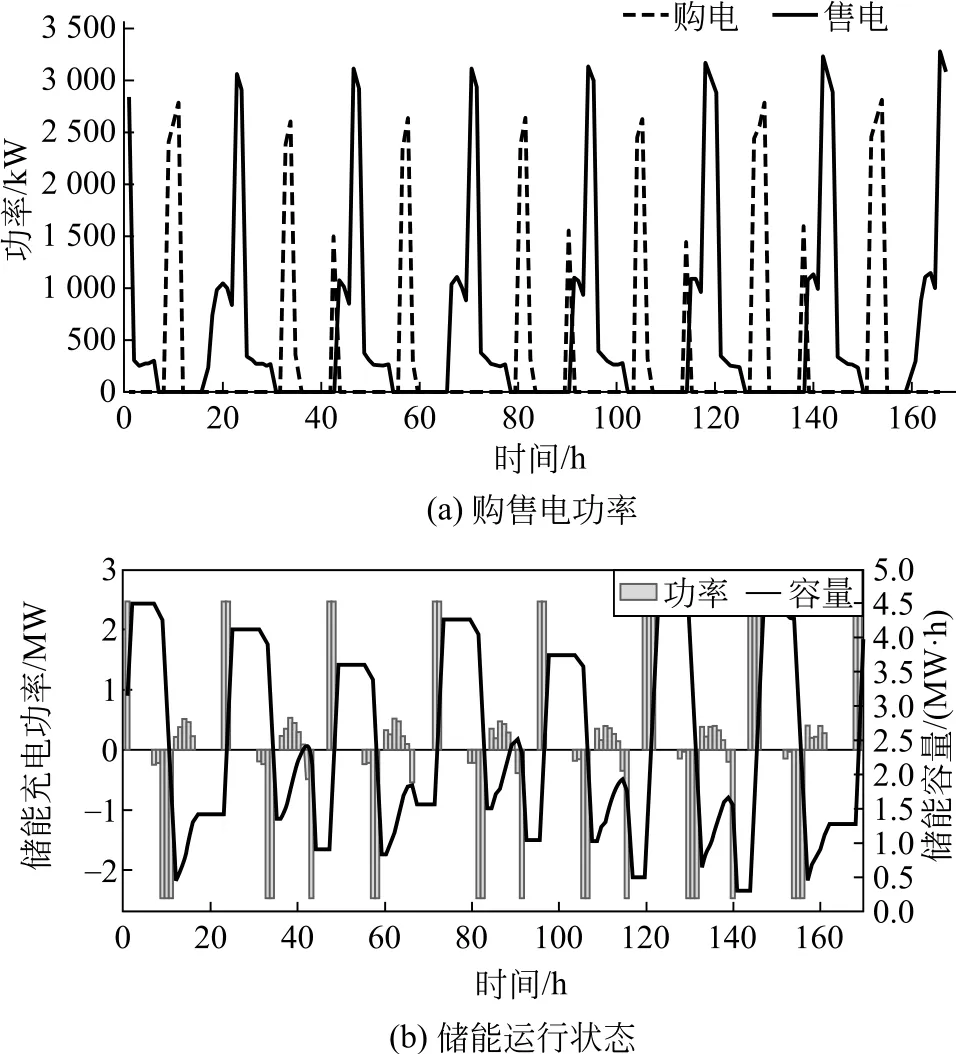
图5 考虑分时电价的购售电功率和储能运行状态Fig.5 Purchase and sale of electricity power and energy storage operation state considerating time-of-use electricity price

实验结果显示,在考虑分时电价进行容量优化后,虽然储能配置容量增加建设成本升高,但系统总成本明显降低。从7日运行结果来看,考虑分时电价后微电网购售电功率明显增加,电池充放电量均有增加,SOC变化范围增大,电池利用率增加。

5 结论

本文针对并网型微电网中储能容量配置不合理造成的系统经济性降低问题,提出了考虑分时电价的储能容量优化方法。首先,建立了储能容量优化配置模型,其次,对社区微电网光伏出力和居民电负荷进行分析,设计了考虑分时电价的系统调度策略,然后,以成本最小化为优化目标,采用粒子群优化算法对模型进行求解,最后,采用某地7日内光 荷历史数据进行容量优化实验,验证了模型的有效性。实验结果表明,该容量优化方法可以降低系统成本,提高储能利用率。