多热源集中供热系统水力性能优化方法
2022-06-07王智伟
杨 红,王智伟
(西安建筑科技大学建筑设备科学与工程学院,陕西省 西安市 710055)
0 引言
江亿院士在《中国建筑节能年度发展研究报告2020》[1]中指出,我国北方供暖能耗占据了建筑总能耗约四分之一,供暖节能是建筑节能的关键部分。供暖节能的实现可以从3个方面入手:热源、热网、热用户。多热源联合供热技术是从热源方面响应供暖节能的手段之一,该技术可以实现热量的按需自由调度,还可以充分配合可再生能源、清洁能源的有效使用。为了充分发挥出多热源供热的优势,在考虑热用户供热可靠性的前提下对热网进行优化是非常必要的手段。
水力计算是多热源集中供热系统设计阶段的重要环节,其准确性和及时性关系到系统的安全经济运行。徐宝萍等[2]提出了一种管网水力条件计算方法,该方法针对水力计算问题的全过程进行了详细系统的论述。李祥立等[3]将最小平方和方法引入水力计算程序中,用来确定管网初始流量分布。王静[4]运用了基本回路法和基尔霍夫定律构建了系统水力工况的数学模型,研制出了一套专门适用于多热源环状管网水力计算的程序。WEI等[5]利用基尔霍夫定律和图论建立了具有3个热源的系统管网数学模型,运用多维背包问题(multidimensional knapsack problem,MKP)建模技术,确定了正常运行工况下管网的供水水流方向。WANG 等[6]建立了网状集中供热系统的管网热动力耦合模型,可以得到所有管道的流向和流量。YAN 等[7]基于基尔霍夫定律,建立了分布式变频泵集中供热系统的水力模型和参数标定方法。LAAJALEHTO 等[8]通过技术和经济分析,研究了具有分布式泵和质量流量控制的环形拓扑集中供热系统的能源效率。VLADIMI等[9]提出了一种复杂管网稳态水力数值模拟与分析的有效方法。WANG 等[10]提出了一种系统水力阻力辨识方法,可以得到系统中所有管道的水力阻力精确值。
多热源集中供热系统涉及多个热源之间的联网运行,这个过程中的热源调度是该领域中备受关注的问题。文献[11-12]给出了不同情况下调峰热源运行方式和承担负荷比例。VERDA 等[13]将储热装置引入到多热源联合供热系统中,配合高效热源的使用时段,增加了高效热源供热量占比。江亿[14]给出了集中供热环状管网的可及性分析概念,可及性分析可以指导环状供热管网的运行调节、优化调度、系统扩容与改造。ZHOU 等[15-17]以多热源集中供热系统水力计算理论为基础,搭建了管网水力优化调度的数学模型。为实际多热源集中供热系统管网优化运行调度提供了理论依据。
当多热源集中供热系统运行时的管网水力工况不处于最佳状态时,系统经常出现供热效率低、能耗消耗高的情况。MOLYNEAUX 等[18]采用一种针对多目标、多模态的进化算法对系统进行运行模拟,提高了系统供热效率,减少了过程中温室气体排放量。WANG 等[19]提出了采用广义简约梯度(general reduced gradient,GRG)算法优化集中供热管网的水泵频率和换热站阀门开度,使系统总泵功最小。LI等[20]在稳态建模的基础上提出了一种综合多尺度建模方法,对热电联产集中供热系统的运行性能进行了仿真。JIE 等[21]利用Matlab软件计算降低泵送热损失成本的优化问题。JIANG等[22]提出了一种基于群搜索优化算法(group search optimizer,GSO)的综合能源直接供热系统的优化运行策略,可以使日常运行中的化石燃料消耗最小化。FANG 等[23]开发了一种基于遗传算法的方法,用于在集中供热管网的不同位置同时优化多个热电厂的热生产,以最小化综合生产和分配成本。ELIS等[24]提出了一种可以对多热源大型集中供热管网的总泵功进行优化的简化模型,其原理是基于正交分解和径向基函数的结合。
本文研究的水力性能优化问题的实质是尽可能增加换热站阀门开度和降低水泵频率,以达到降低管网系统压力损失的目的。建立了一种优化调节策略,是以图论的方法建立具有网状拓扑结构的多热源集中供热系统数学模型,结合协同论的思想,在质量和能量平衡的基本物理理论下,建立系统优化方程,引入热源调度性因子,利用粒子群优化算法(particle swarm optimization,PSO)求解非线性数学方程组,所得的最优解即为在充分保证各换热站供需平衡的前提下实现最小能耗的流量组合。
1 模型建立
在建模之前,首先对本研究中模型建立依靠的基础假设加以说明:
(1) 假设供回水管网对称分布,所有供给换热站皆为供热不供水,且系统中无泄漏点。
(2) 各换热站的需求热负荷随着室外气象参数线性变化。
(3) 假设各换热站使用的末端散热装置相同,即各末端对于供回水温度的需求相同。
1.1 系统数学模型
应用图论对多热源供热系统管网的水力条件进行建模[25]。模型中包括了供水管道、回水管道、换热站和热源,用以获取管网的水力工况。整个集中供热管网被看作是一个有向图。该有向图有3个基本元素,即节点、分支以及分支的方向。
根据图论中的基尔霍夫定律(Kirchhoff's law),各节点的净流量为0,各回路中所有支路压降的代数和为0。用矩阵方程表示为

式中:Bk为基本关联矩阵,其行号代表节点数,列号代表分支数,其基本元素定义为

Cf为独立回路矩阵,其行号代表回路数,列号代表分支数,其基本元素定义为

G 为分支流量向量,其元素是管网中分支的流量值gi(i=1,2,…,n),即
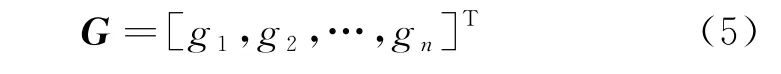
ΔP 为分支压降向量,其元素是管网中分支的压降值Δpi(i=1,2,…,n),即

为了实现水力计算与优化,需要重新排列矩阵和向量。向量G 和向量ΔP 重新排列为式(7)(8)[26]的形式:
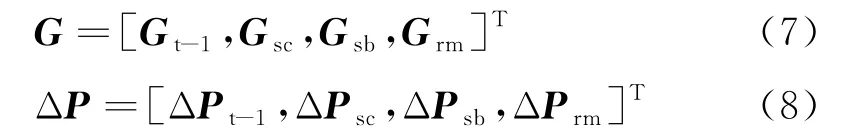
式中:下标“t-1”表示不包括热源树枝的树枝集;下标“sc”表示热源树枝集;下标“sb”表示换热站树枝集;下标“rm”表示余枝集。即:

同样,矩阵Bk和Cf也按照向量G 和向量ΔP的顺序重新排列为:
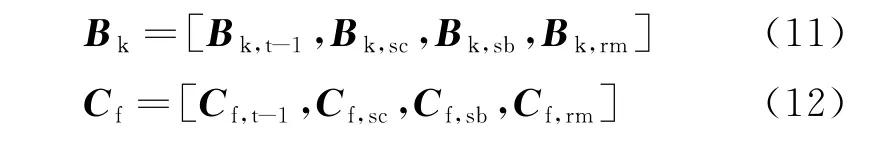
1.2 管网阻力模型
管网系统阻力模型可以表述为:
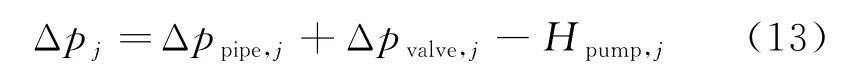
式中:Δppipe,j为管道压降;Δpvalve,j为调节阀压力损失;Hpump,j为水泵泵头。
管道的压降包括管道沿程阻力损失和通过各种局部阻力构件以及设备时产生的局部阻力损失。根据Darcy-Weisbach公式,管道压降为
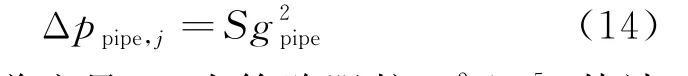
式中:gpipe为管道流量;S 为管路阻抗,s2/m5,其计算公式为
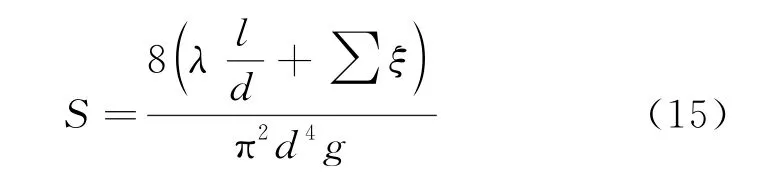
式中:λ 为沿程阻力系数,采用Альтщуль半经验公式(公式(16)[27])得到;l 为管道长度,m;d 为管道直径,m;ξ 为沿程阻力系数;g 为重力加速度。
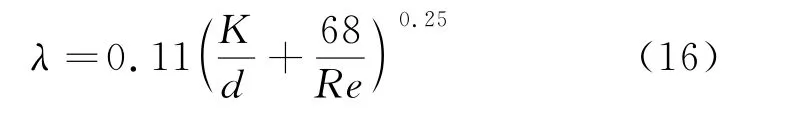
式中:K 为管道粗糙度,m;Re 为雷诺数,惯性力与黏性力之比。
管网中控制阀的流量特性为等百分比特性[28],根据等百分比阀门流量特性计算公式以及阀门的节流原理,可以推出阀门压降为

式中:Δphs,j为热源压降;Shs为热源处阻抗;ghs为热源供应流量;Δpsub,j为换热站压降;Ssub为换热站处阻抗;gsub为换热站需求流量;Δpvalve,j为换热站处阀门压降。
根据《实用供热空调设计手册》,热网水泵出口和热源内部压力损失一般在80~150 kPa,热源内的除污器及由除污器至热网水泵入口的压力损失一般为20~50 kPa[30]。
1.3 优化方程建立
集中供热管网水力性能优化是指在多个水力方程和允许的约束条件下,通过增加换热站阀门开度和降低水泵频率,达到使整个管网系统总泵功最小的目的。该优化问题可以表达为公式(23)的形式。由于其中的回路压力平衡方程组属于非线性方程组,需要采用数值计算方法求解[25]。
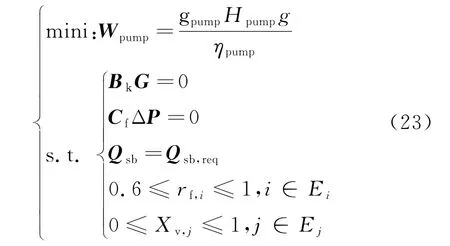
类比协同论中绝热消去原理[31],认为每个供暖段中供水流量保持稳定,也即与时间无关,便可以将树枝流量视作快弛豫参量,将余枝流量视作慢弛豫参量,用余枝流量替换所有树枝流量,得到的回路压力平衡方程组中未知数数目与方程组数目相等,即
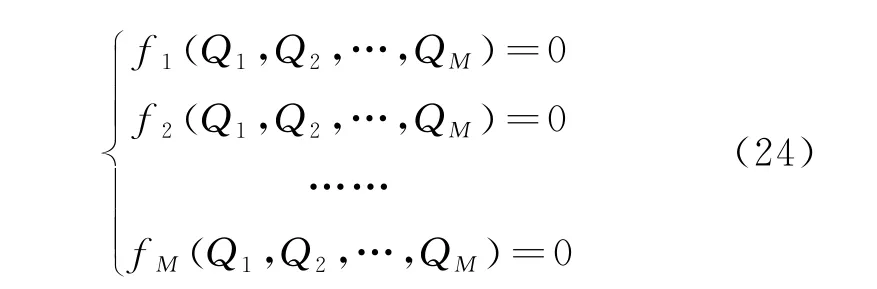
式中:Q1,Q2,…,QM为M 个余枝管段流量。
2 实例应用
2.1 系统介绍
本节以某多热源集中供热系统为对象,模拟了优化调节策略的应用效果。该系统的图论布局如图1所示,系统中共包括3个热源,106个换热站,450个节点,571条分支,122个独立回路。
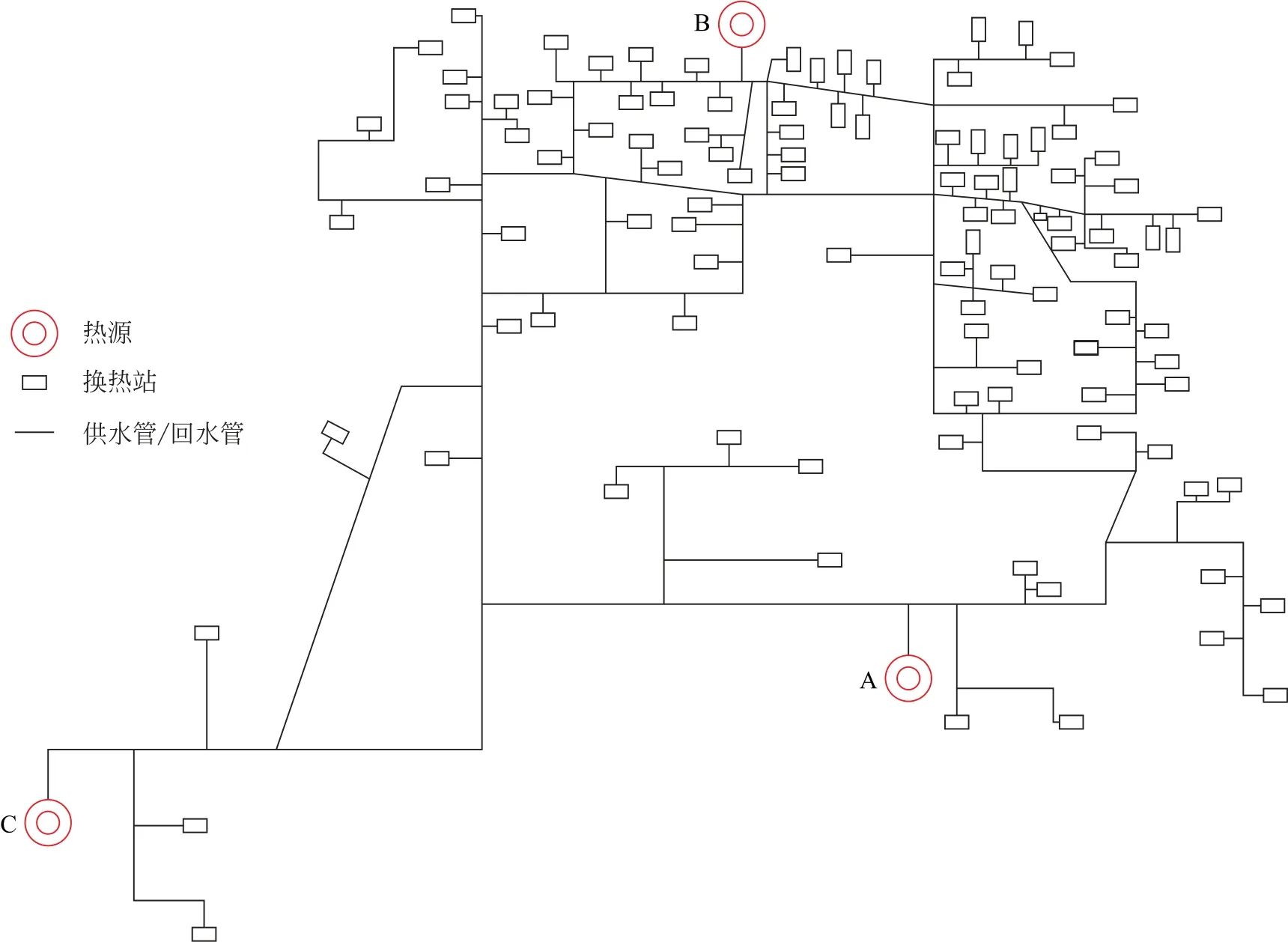
图1 多热源集中供热管网图论布局Fig.1 Schematic layout of multi heat source central heating pipe network
系统中,热源A 为燃煤锅炉,总装机容量为265 MW,配备4台循环水泵,扬程为70~75 m;热源B为燃气热水锅炉,总装机容量为145 MW,配备4台循环水泵,其中3台扬程为70 m,第4台扬程为70 m;热源C的热量取自热电厂,总换热容量为476 MW,配备4台循环水泵,其中2台的扬程为120 m,另外2台扬程为105 m。
该多热源集中供热管网系统采用分阶段改变流量的策略运行,供回水温度为130℃/70℃。
2.2 热源调度性设置
为响应节能减排的国家政策,在该系统中提出了热源调度方案:随着负荷率的降低,逐步减少燃煤热源供应量,增加燃气热水热源和热电厂热源的供应量。
具体方法为:在优化程序中引入热源偏好性因子Di(i 为热源编号),设置各热源初始偏好值为Di=1/3,该值随程序进行逐步更新,并设置限制条件为
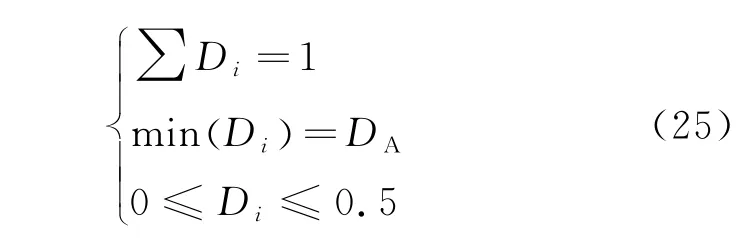
2.3 优化方程建立及求解
式(18)(20)中出现的泵参数见表1。供暖换热站满负荷时的流量需求总结在了表2中。
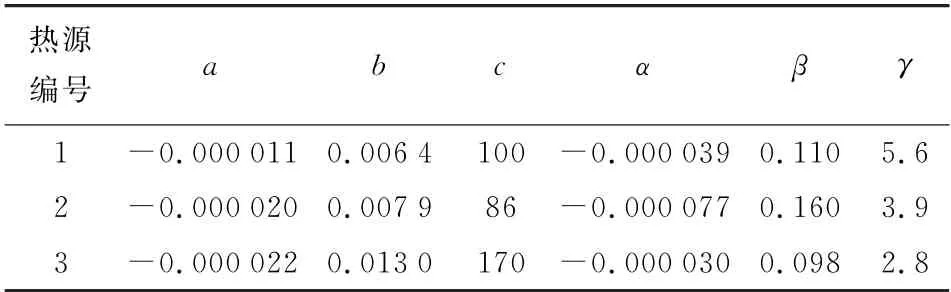
表1 热源泵参数Table 1 Heat source pump parameters
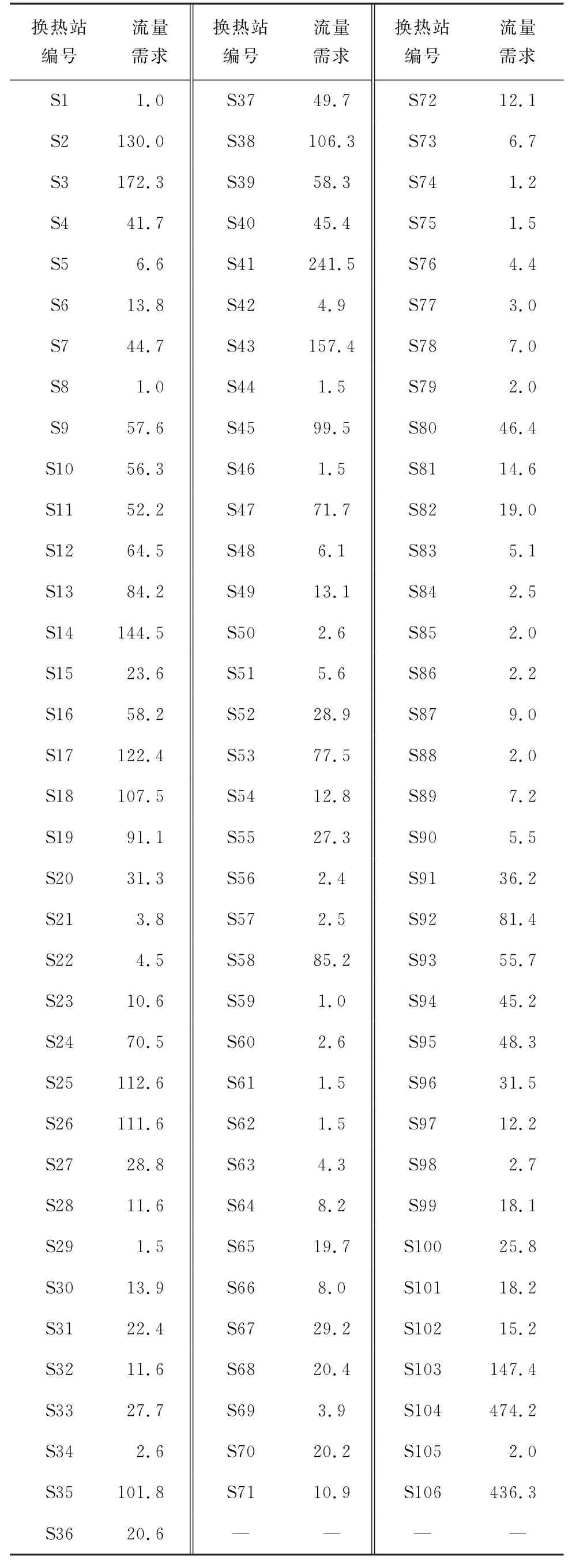
表2 换热站满负荷时的流量需求Table 2 Flow demand of heat exchange station under full load t/h
式(24)所示的协同优化模型是非线性方程组,其求解是一个巨大的挑战。本文采用随机搜索智能算法——粒子群优化算法(particle swarm optimization,PSO)进行求解。图2给出了求解流程。
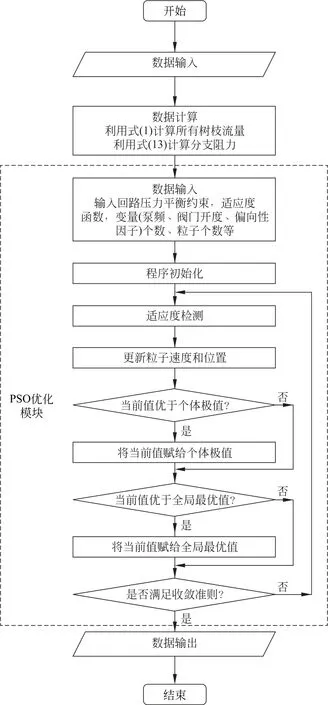
图2 优化方程求解流程Fig.2 Flow chart of solving optimization equation
3 结果分析
3.1 供需匹配度评价
本研究忽略了管网水量损失,故设置各换热站实际供水量为理论供水量的1.06~1.15倍,并总供水量为理论总供水量的1.0~1.1倍,以控制优化结果即可满足实际需求,又可达到优化目的。
优化调节策略下不同负荷率下各换热站的供需匹配度结果以及管网系统总供需匹配度结果展示在图3—4中。可以看到,优化调节策略可以实现针对供需匹配所提的约束条件,在满足各换热站的供需匹配度前提下,保证系统供需匹配维持在限定范围内。
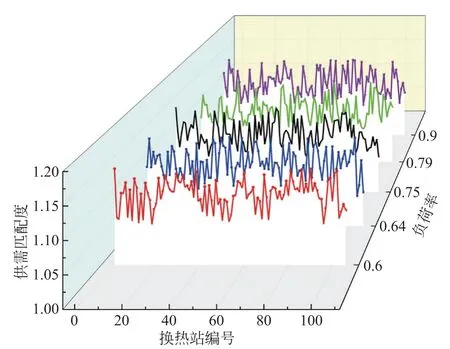
图3 优化调节策略下各换热站的供需匹配度Fig.3 Matching degree of supply and demand of each heat exchange station under optimal regulation strategy
3.2 管网动力系统评价
本节对比了优化调节策略和控制压差调节策略下系统的泵功与泵头。控制压差策略的核心是保证管网系统在最不利工况下控制点的压差恒定。
图5比较了2种调节策略下的泵功值。从图5可以看到,不同负荷率下热源A—C 的泵功降低率分别为19.8%~21.8%、20.8%~22.7%、17.8%~19.7%,3个热源的总ΔW 为19%~20.8%。随着负荷率的增加,ΔW 值逐渐降低,这是因为当负荷率接近满负荷时,优化调节策略的能耗降低空间会逐步降低。在负荷率为0.75时,ΔW 值达到了峰值,说明优化调节策略在负荷率为0.75时的效果最好。
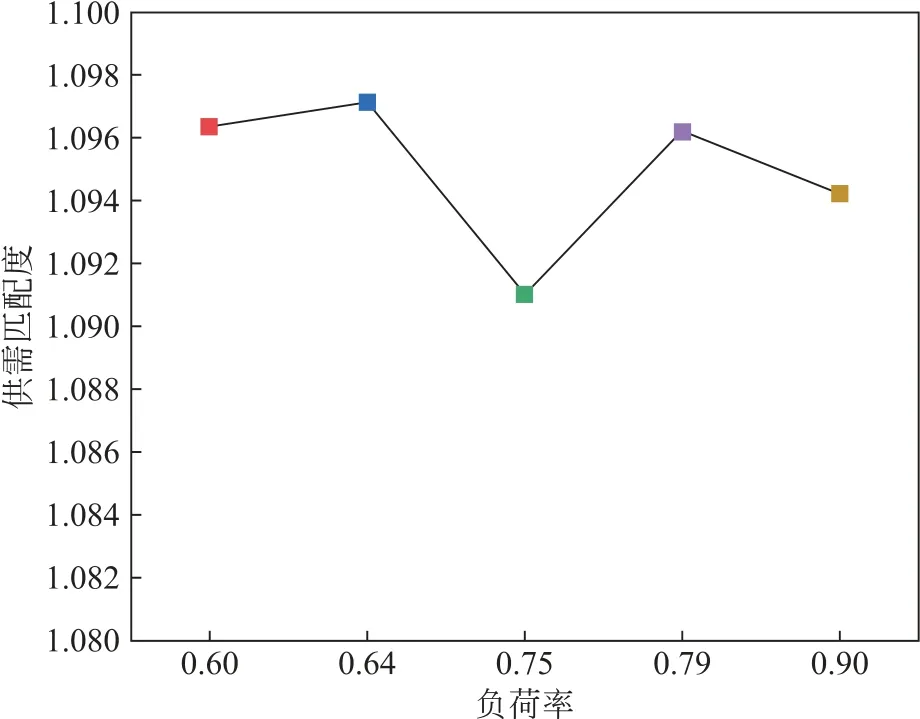
图4 优化调节策略下管网系统的供需匹配度Fig.4 Matching degree of supply and demand of pipe network system under optimal regulation strategy
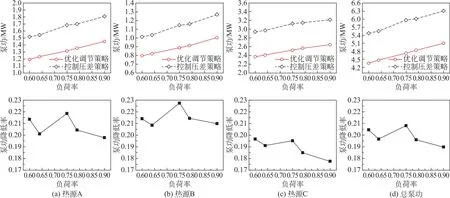
图5 热源泵功Fig.5 Heat source pump work
图6比较了2种调节策略下热源泵的泵头值。可以看到,相较于压差控制策略,优化调节策略下,热源A—C的泵功削减范围分别为13.6%~15.1%、9.1%~12.8%、8.5%~12.7%。并且随着负荷率的增加,泵头削减比例总体呈现降低的趋势,这也是因为在靠近满负荷时,优化调节策略的可优化空间逐步减小。
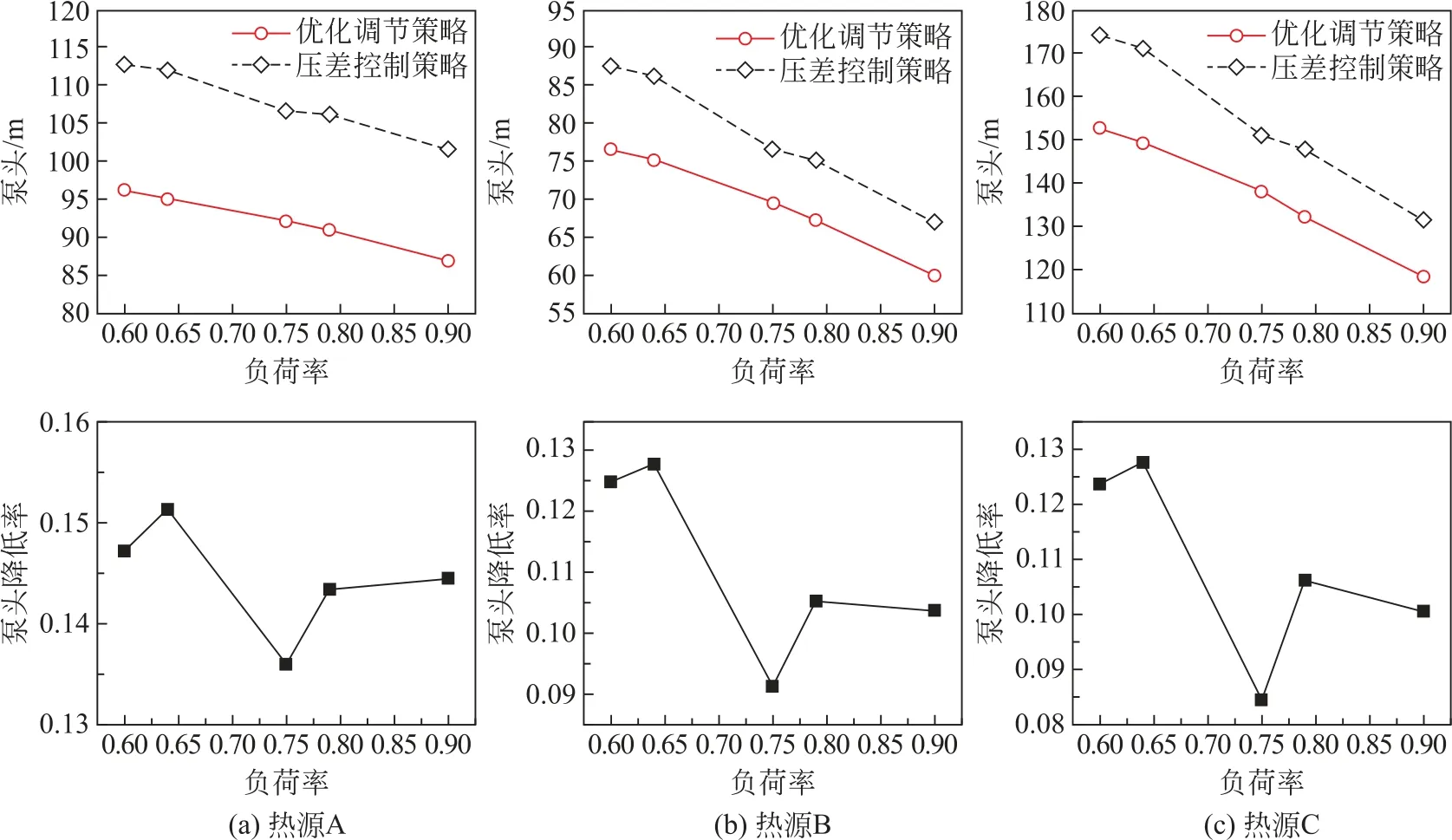
图6 热源泵头Fig.6 Heat source pump head
图7比较了2种调节策略下热源泵的运行效率值。从图7可看出,优化调节策略和压差控制策略下的水泵效率值并没有固定的规律:热源A 处,优化调节策略的泵效率低于压差控制策略,热源B处,优化调节策略的泵效率高于压差控制策略,而热源C处,负荷率为0.75以下,压差控制策略下泵效率高,负荷率0.75以下,优化调节策略下的泵效率高。这表明,对于确定的管网系统,单纯提高泵效率并不能得到最优水力工况,要实现水力性能的优化运行,需要考虑总集中供热管网的约束条件。
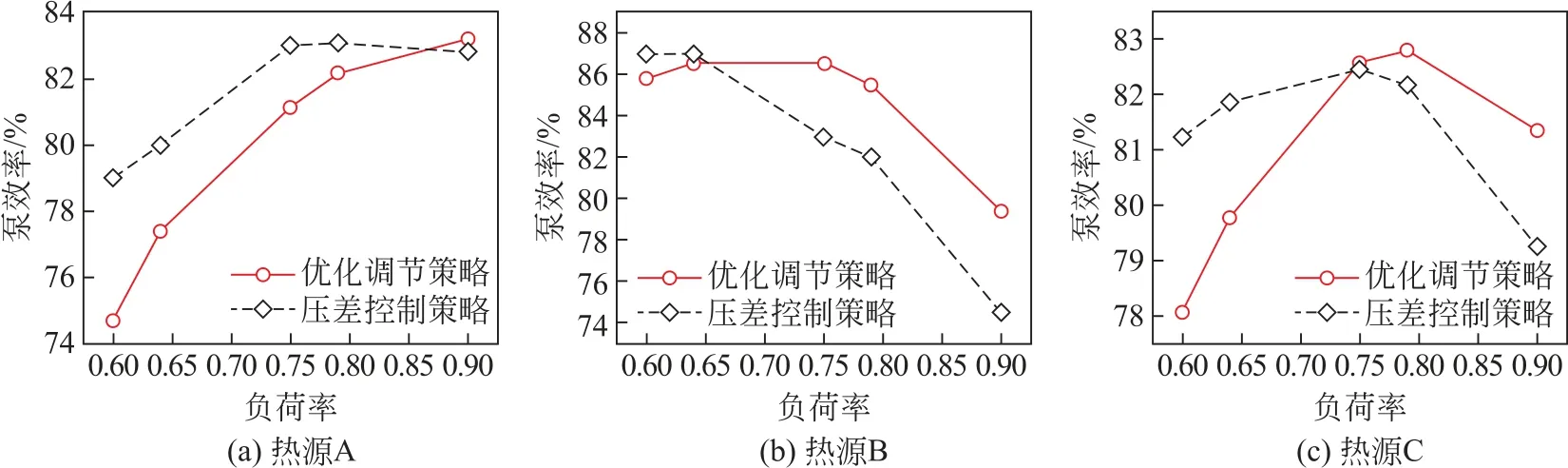
图7 热源泵效率Fig.7 Heat pump efficiency
3.3 热源调度性评价
本节对比了是否考虑热源调度性(即是否引入热源偏好性因子)的系统水力性能,包括不同负荷率下各热源供给流量和泵功的对比。
图8比较了不同负荷率下考虑热源调度性前后的流量分布。从图8可以看出,在优化程序中加入热源偏好性因子后,燃煤热源A 的供给量减少,并随着负荷率的降低,减少量逐步增加;燃气热水锅炉B的供给量增加;取自热电厂的热源C 在负荷率高于75%时供给量减少,低于75%时供给量增加。这是由于热源偏好性因子在高负荷率下的热源出力为等比设置,当负荷率逐渐降低时,根据热源调度性的设置原则,A 热源占比逐渐降低,B、C 热源占比逐渐增加。由图8可知加入热源偏好性因子后优化结果达到了对于热源调度性的设置目标。

图8 考虑热源调度前后热源流量对比Fig.8 Comparison of heat source flow before and after considering heat source scheduling
图9比较了不同负荷率下考虑热源调度性前后的泵功值。从图9可以看到,在优化程序中加入热源偏好性因子后,不同热源的泵功变化趋势与流量变化相同,而系统总泵功随负荷率的增加呈现略微上升趋势,增加率为-0.43%~1.56%,本研究认为可将该增加部分认为是对于能源调度的牺牲动力而忽略。
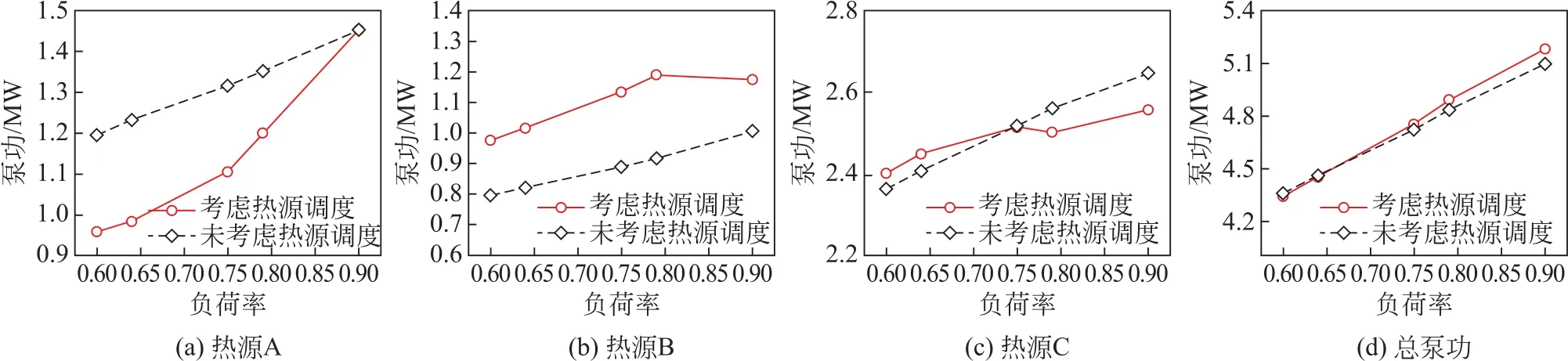
图9 考虑热源调度前后热源泵功对比Fig.9 Comparison of heat source pump power before and after considering heat source scheduling
4 结论
本文针对多热源集中供热系统获取最优水力工况困难的情况,提出了一种优化调节策略,该策略以图论为理论基础,结合协同论的思想,建立优化方程后用粒子群算法进行求解,以求得在保证系统供热可靠性的前提下使动力系统能耗最小的设备开启情况组合。研究结论如下:
(1) 本文忽略了供回水管网的差异性以及管网的水量损耗,设置了各换热站实际供水量为理论供水量的1.06~1.15倍,并总供水量为理论总供水量的1.0~1.1倍的约束条件。从研究结果中可以看出,优化调节策略可以满足该约束条件,实现管网系统的最佳供需匹配,实现了减少因为能源供给侧和能源消费侧的不平衡差异带来的能源浪费。
(2) 本研究对于动力系统优化结果主要以总泵功降低率的形式给出。从研究结果可以看到,优化调节策略相较于压差控制策略可以降低21%的总泵功。可以实现在供需平衡的基础上尽可能降低系统能源消耗的目的。同时,本研究给出了优化调节策略下系统的泵功、泵头、泵效率在不同负荷率下相较于压差控制策略的变化情况,可以看到优化调节策略可以有效降低能耗系统的泵功和泵头值。但泵效率值变化趋势却并不规律,这说明在不考虑集中供热管网水力约束的情况下提高泵的效率并不能得到系统最优工况。单纯调高泵效率值对于系统的水力工况并不有利。
(3) 本文为满足能源调度目标,在优化程序中引入了热源偏好性因子,结果表明,通过牺牲少量动力能够达到减少燃煤锅炉供给热量的调度目标。
