一类具有同类相食的昆虫传染病模型分析
2022-06-07马杏园邱志鹏
马杏园,邱志鹏
(1.南京理工大学 理学院,江苏 南京 210094;2.南京理工大学江阴校区 基础教学与实验中心,江苏 无锡 214443)
0 引言
种群中不同发育阶段之间的同类相食是自然界普遍现象[1-3]。一些学者认为同类相食在食植昆虫中普遍存在,如蚂蚁[4]、蜜蜂[5]和沙漠蝗虫[6]。同类相食在时空上深刻影响种群的年龄结构和物种丰盛度,在简单的近缘物种组成的群落中也起关键的调节作用,使得简单的食物网变得更为复杂。对同类相食的研究有助于理解物种丰盛度的内部调节机制,也能在一定程度上解释物种间的生态位重叠[7-8]。近年来,许多学者建立了具有同类相食现象的阶段结构模型,研究其相应的动力学性态[9-12]。结果表明,同类相食是一种重要机制,可以通过提高种群的生长速度、存活率、寿命和繁殖力来提高种群的适应度,为种群提供在恶劣环境下生存的能力。
生态学和传染病学是两个不同的研究领域。然而,在有些情况下,社会性昆虫会携带一系列病毒,对种群动态产生重大影响。变形翅病毒(DWV)和瓦螨破坏性病毒(VDV1)是最广泛的蜜蜂病毒,这些RNA病毒严重影响蜜蜂的健康,并导致全球蜂群损失率上升[13]。文献[14]率先将种群传染病动力学模型与捕食者-食饵模型结合起来,研究传染病对捕食者-食饵模型的影响[15-17]。生态流行病学是理论生物学研究中的一个重要分支,开展此类研究可以更好地理解疾病对种群的影响。本文将SI传染病模型引入到一类具有两个阶段结构的同类相食模型[18],研究传染病模型与同类相食模型之间的相互影响。
1 模型的建立
基于文献[18]的假设,我们把昆虫种群分为卵和成虫(包括幼虫、蛹和成虫)两个阶段,传染病只在成虫中传播,因此成虫又被分为易染成虫和染病成虫。分别用 E(t)、S(t)、I(t)表示t时刻卵、易感染成虫和染病成虫的数量。假定卵只会因同类相食而死亡,成虫中疾病发生率是双线性感染率[19]。并且由于疾病的影响,染病的成虫没有繁殖能力和同类相食能力,同类相食行为只会对易感染成虫的死亡率有影响。在此假设下,模型流程图如1所示。
基于图1,我们建立了具有同类相食行为的昆虫传染病模型

图1 模型(1)关于卵、易感染成虫和染病成虫结构图Fig.1 Transfer diagram of model(1)in terms of eggs,susceptible adults ltand infective adults
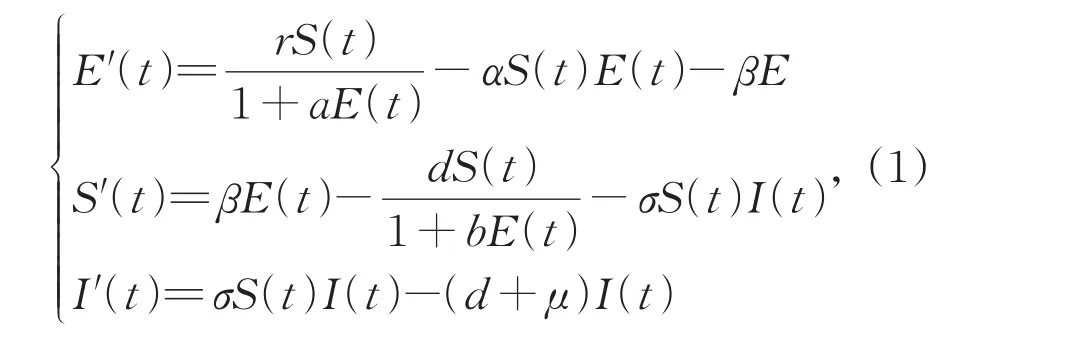
其中r为单个易感染成虫的产卵率;α为单个易感染成虫的食卵率;β为卵向成虫的转化率;d为种群中成虫的自然死亡率;σ为传染病的感染率;b为描述同类相食行为对易感染成虫死亡率的影响系数,因此b的值与α密切相关且α=0时b=0;μ是由疾病引起的额外死亡率;这里所有的参数都是非负数。

2 动力学分析
本节我们主要讨论模型(1)的动力学性态。在分析系统(1)的复杂动力学性态前,我们首先考虑系统不存在传染病时的边界性态,这时系统(1)简化为




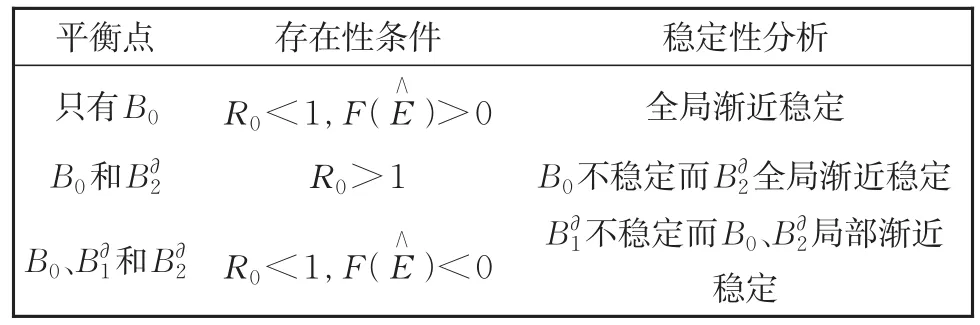
表1 系统(2)的平衡点及其稳定性Table 1 Equilibria and their stability of model(2)




3 数值模拟
本节对上述结论进行数值仿真。为验证上述结论,利用Matlab对前文的理论分析进行数值模拟。
(1)当α>bd时,系统(2)在R0=1时会产生前项分支,此时系统(2)有唯一全局渐近稳定正平衡点。当α<bd时,系统(2)在R0=Rδ时会产生后项分支,此时系统(2)在R△<Rδ<R0<1区间内有两个局部渐近稳定点和,如图 2 所示。

图2 模型(2)在 α>bd(a)和 α<bd(b)时的分支图Fig.2 Bifurcation diagrams of the model(2)whenα>bd(a)andα<bd(b),respectively
(2)在 系 统(1)中 取r=1,a=0.001,α=0.000 1,β=0.999,d=1,b=1,σ=0.5,m=0.5,此 时 系 统 (1) 的 正 平 衡 点 (E*,S*,I*)=(2.4,2.4,1.4)是局部渐近稳定的,如图 3 所示。
(3)在 系 统(1)中 取r=1,a=0.001,α=0.000 1,β=0.999,d=1,b=1,σ=2,m=0.2,此时系统(1)的正平衡点(E*,S*,I*)是不稳定的,如图4所示会产生Hopf分支和极限环分支。

图4 模型(1)在r=1,a=0.001,α=0.000 1,β=0.999,d=1,b=1,σ=2,m=0.2时的Hopf(a)和极限环(b)分支图Fig.4 Hopt bifurcation(a)and limit cycle(b)diagram of the model(1)at r=1,a=0.001,α=0.000 1,β=0.999,d=1,b=1,σ=2,m=0.2
(4)在图3中,系统有唯一局部渐近稳定的正 平 衡 点 (E*,S*,I*),即 种 群 中 存 在 传 染 病 。在图5中,系统有唯一局部渐近稳定的边界平衡点(E*,S*,0),即种群中不存在传染病。 图3和图5的对比表明,我们的模型与疾病防控有关,当选取适当的参数时,同类相食行为可以消除种群中的传染病。
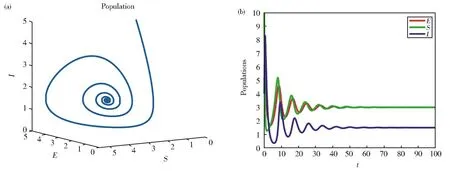
图3 模型(1)在 r=1,a=0.001,α=0.000 1,β=0.999,d=1,b=1,σ=0.5,m=0.5时的空间(a)和平面(b)图Fig.3 Spatial(a)and plan(b)diagram of the model(1)atr=1,a=0.001,α=0.000 1,β=0.999,d=1,b=1,σ=0.5,m=0.5
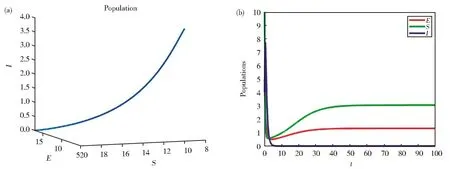
图5 模型(1)在r=1,a=0.001,α=0.43,β=0.999,d=1,b=1,σ=0.5,m=0.5时的空间(a)和平面(b)图Fig.5 Spatial(a)and plan(b)diagram of the model(1)at r=1,a=0.001,α=0.43,β=0.999,d=1,b=1,σ=0.5,m=0.5
4 结论
本文研究昆虫种群中的同类相食行为对虫传染病模型的影响,采用具有双线性感染率的SI模型描述传染病在成年种群的传播,且传染病会导致成年种群死亡率增加。在该模型中,种群被分为三个部分,即卵、易感染成虫和染病成虫,且种群中存在同类相食行为。通过对系统(1)的分析得到该模型最多有4个平衡点,即3个无病平衡点和1个正平衡点。由仿真结果可以看出,传染病模型和同类相食模型之间互相影响,当选取合适的参数时,同类相食现象可以有效消除种群中的传染病,可以用作传染病入侵的控制剂。
此模型是具有实际意义的,例如在欧洲和美国,蜜蜂群体损失与瓦螨有关。这种寄生虫以蛹和成年蜜蜂的内部组织为食,在此过程中可以携带大量RNA病毒。这些病毒包括变形翅病毒(DWV)和瓦螨破坏性病毒(VDV1)。另一实例为在过去的十年中,生物学家在火蚁中发现四种病毒,这些是第一个完全由蚂蚁描述的病毒。其中三种病毒是单链RNA病毒,最后一种是DNA病毒,这些病毒在火蚁种群中引起显著的死亡率。而在蜜蜂和蚂蚁种群中,成虫对卵的残食现象很普遍,因此我们的模型是具有生物应用的。
