细说基本不等式在求最值时的“变形”

丁伟伟

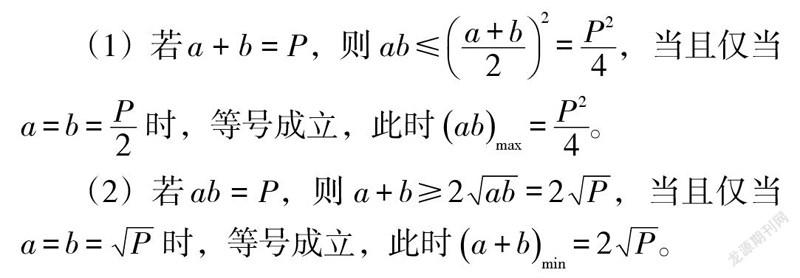
摘  要：基本不等式主要体现的是不等关系，在解题的过程中會涉及“变形”，学生难以把握本质，琢磨不定。虽然教师给出了一些变形的模式，但是始终未触及根本。基于此，文章从基本不等式求最值的原理入手，逐渐揭开变形的本质——换元，让学生抓住变通之道，培养数学学科核心素养。

关键词：基本不等式;最值;换元;核心素养

数学学习的关键是概念。基本不等式知识点蕴含了换元思想，命题者正是运用这种思想，通过先换元再变形，加强知识应用的难度。因此，从解题者的角度来看要学会逆向思考，如何变形成为解题的关键。

一、基本不等式求最值的原理

基本不等式求最值的原理是：积定和最小，和定积最大，用符号语言表述为：已知a > 0，b > 0，P为常数。

G.波利亚在《怎样解题：数学思维的新方法》一书中强调，理解题目，包括未知量是什么，已知数据是什么，条件是什么。基本不等式求最值的原理本身也是一个命题，它呈现的题设和结论涉及两种运算（和与积）、一个不等号、一个定值、两个正对象，而变形的设置往往也从这几个方面谈起。

1. 从两种运算和不等号方向谈变形

下面是苏教版《普通高中课程标准实验教科书·数学5必修》“13.4 基本不等式”的课后习题及其变形，变形正是从两种运算和不等号的方向入手。

（1）若x > 0，y > 0，且2x + 5y = 20，求lgx + lgy的最大值。

第（2）小题中涉及三个字母，显然不能孤立地作为研究对象。目标求的是积运算的最大值，条件中是和为定值，从运算和不等号方向来看均无矛盾，但是两个对象前后不统一，结合目标分析，可以通过换元最终统一研究对象。

第（3）小题可以从以下两个角度实现研究对象的一致。一是从定值条件入手，此题定值条件不明显，可

由此，当未知量较多时，往往通过减元或换元，结合其他变形角度，确定研究的两个正对象。

综上可知，运用基本不等式求最值，变形不外乎从两种运算和不等号方向、定值条件、两个正对象入手，变形的目的最终是为了换元，从而明确研究的两个正对象。

参考文献：

[1]中华人民共和国教育部制定. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.

[2]G.波利亚. 怎样解题：数学思维的新方法[M].涂泓，冯承天，译. 上海：上海科技教育出版社，2007.

[3]李邦河. 数的概念的发展[J]. 数学通报，2009，48（8）.

[4]余建国. 基于模式识别的“基本不等式的应用”教学分析[J]. 中国数学教育（高中版），2014（3）.

[5]李世桂. 细说基本不等式求最值问题的常见结构与方法[J]. 中学数学教学参考（上旬），2019（12）.90E1B3F6-E98F-4450-BCC4-32AB99267384