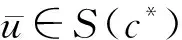Kirchhoff型方程约束基态解的存在性
2022-06-06王淑丽郭祖记
陈 宏,王淑丽*,郭祖记
(太原理工大学 数学学院,山西 太原 030024)
Kirchhoff方程是微分方程中的一类典型问题,它产生于弹性力学以及人口动力学中,在非牛顿力学、宇宙物理、血浆问题和弹性理论等诸多领域都有广泛应用,因此研究此类方程具有深刻的物理意义.1883年,Kirchhoff[1]在研究弹力绳自由振动的经典D’Alembert波方程时导出了下列方程
该方程考虑到了弹力绳横向振动引起的长度变化.上述方程的稳态形式为
其中a,b是正常数,Ω⊂RN是有界区域.上述问题可作为物理和生物等相关系统的数学模型[2-5],因此受到了人们的广泛关注.
近年来,对于带约束的非线性Kirchhoff方程已有一些研究成果.1997年,Ye[6]使用山路定理获得了方程
Δu-f(u)=λu,u∈H1(RN)
约束解的存在性;2014年,Jeanjean[7]利用极小化序列和消失引理获得了方程
约束解的存在性,其中λ∈R;2018年,Xie等[8]利用变分法和山路定理获得了方程
约束解的存在性和多重性.
1 主要结果
文中考虑非线性Kirchhoff方程

首先对f作如下假设:
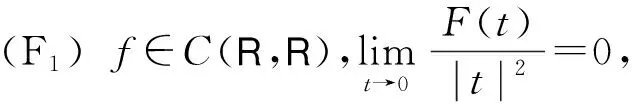
|f(t)|≤C0(1+|t|q-1);
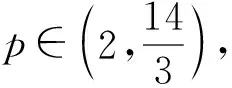
(F3)对所有的t∈R,有
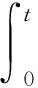
受文献[7,8]的启发,本文利用变分法中的极小化序列和消失引理方法证明Kirchhoff方程(1)约束基态解的存在性.为了得到这样的解,我们寻找泛函
在集合
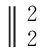
上的极小元.记
c*:=inf{c∈(0,+∞):m(c)<0},
其中
显然,如果uc∈S(c)满足Ia(u)=m(c),则uc是方程(1)的约束基态解.
我们的主要结论如下:
定理1假设条件(F1)~(F3)成立,则c*>0且
1)对每个c>c*,m(c)有极小元且m(c)<0;
2)存在a0>0使得当a>a0时,m(c*)有极小元且m(c*)=0.
2 预备知识
本文做下列约定:
( i )通常Sobolev空间H1(R3)中,其内积和范数分别为
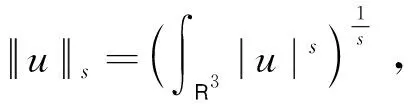
(iii)Ci表示不同的正常数,其中i∈N+;
(iv)对于任意的x∈R3,r>0,记
Br(x)={y∈R3:|y-x| 引理1(Gagliardo-Nirenberg不等式[9]) 设N≥2,则对于任意的q∈[2,2*),存在依赖于N和q的常数CN,q,简记为C(q),使得 引理2(消失引理[10]) 若{un}在H1(RN)中是有界的,且对某个r>0和2≤q<2*,有 则对所有2 引理3假设条件(F1)成立,则 1)对任意的c>0,m(c)有定义,并且m(c)≤0. 2)m(c)在(0,∞)上是连续的. 3)如果条件(F2)和(F3)成立,则存在c0>0,当c>c0时,有m(c)<0. 证明1) 由条件(F1),对于任意的ε>0存在Cε>0,使得 |F(t)|≤ε|t|2+Cε|t|q,t∈R. (2) 在(2)式中取ε=1并结合Gagliardo-Nirenberg不等式,对u∈S(c),有 由于2<3(q-2)/2<4,所以Ia(u)在S(c)上是下方有界的. 对t>0和u∈H1(R3),令 ut(x):=t3/2u(tx),x∈R3, 显然对u∈S(c)有ut∈S(c).因此,当u∈S(c)时,由条件(F3)可得 又由(2)式可得 2)对任意的c>0,取cn>0满足cn→c.对于每个n∈N,取un∈S(cn),使得 结合(3)式可知{un}在H1(R3)中有界,因此 另一方面,取{vn}⊂S(c)是m(c)的一个极小化序列,则 3)由条件(F2),存在δ0>0,ρ0>0,使得 F(t)≥δ0|t|p, ∀|t|≥ρ0. (7) 令 {c∈(0,+∞):m(c)<0}≠∅, 故c*=inf{c∈(0,+∞),m(c)<0}有定义.】 引理4假设条件(F1)~(F3)成立,则 1)c*>0; 2)对于任意的c>c*,有 证明1) 由c*的定义,只需证明存在θ>0,使得m(θ)≥0即可.由条件(F3)可知, F(t)≤C1(|t|10/3+|t|q), ∀t∈R. (11) 再结合Gagliardo-Nirenberg不等式,则对任意的u∈H1(R3),有 对于任意的u∈S(θ),由(12)式可得 由Young不等式可得 取θ>0,使得 则由(14)和(15)式可得,对所有的u∈S(θ),有Ia(u)≥0,从而m(θ)≥0,所以c*>0. 2)由条件(F3)可知,当t≥1时,有 F(t1/2u)≥t5/3F(u). (16) 对于任意的c>c*,取{un}⊂S(c),满足Ia(un)→m(c).下证存在一个常数τ>0使得 若不然,则存在{un}的子列{unk},仍记为{un},使得||un||2→0.由引理3之结论3)和2)有 这是个矛盾,因此(17)式成立.当c>c*,t>1时,对任意的u∈S(c),由(8)和(16)式可知 令n→∞,则 这表明 m(tc) (19) 由结论1)可知,当0 情形1当α>c*,c-α>c*时,由(19)式有 情形2当α>c*,c-α≤c*时,m(c-α)=0,又c/α>1,所以由(19)式有 情形3当α≤c*,c-α>c*时,证明与情形2类似. 情形4当α≤c*,c-α≤c*时,m(α)=0,m(c-α)=0,所以亦有m(c) 综上可知,(10)式成立.】 1)证明对于任意的c>c*,m(c)存在一个极小元.对每个c>c*,取{un}⊂S(c)使得Ia(un)→m(c).(3)式表明{un}在H1(R3)中是有界的,我们断言 这是个矛盾.因此存在{yn}⊂R3,满足 根据引理3之结论2),有 2)证明m(c*)是可达的.对于每一个n∈N,取cn=c*+1/n,由引理3之结论3)和1)的证明可知,存在un∈S(cn),使得 根据引理3之结论2),有Ia(un)=m(cn)→m(c*)=0.(3)式表明{un}在H1(R3)中是有界的,我们断言(20)式成立.如果δ=0,则根据集中紧性原理,在Ls(R3)中有un→0,其中2

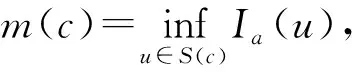
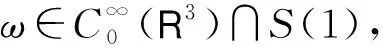
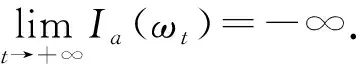
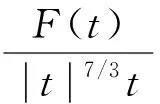
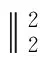
3 定理1的证明