一类基于特征函数构造的极小线性码
2022-06-06杜小妮王天心金文刚
杜小妮,王天心,金文刚
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
0 引言
线性码具有良好的代数结构和高效的译码算法,因此广泛应用于通信、信息安全和数据存储系统等领域.一般情况下,确定线性码的长度、维数和最小距离是比较困难的,能确定重量分布的码字只占很小的一部分,因此,线性码的构造及其重量分布一直是密码学者关注的课题.具有较低重量的线性码可被应用于认证码[1]、结合方案[2]、强正则图[3]和构造具有良好访问结构的秘密共享方案[4]等领域,极小线性码在秘密共享方案[4]和两方安全计算[5]中扮演着重要角色.一般地,具有较低重量的极小线性码可以通过选择不同的定义集[6]来构造,且大多数满足Ashikhmin-Barg条件.2018年,Chang等[7]提出了一类不满足Ashikhmin-Barg条件的极小二元线性码;Heng等[8]构造了一类不满足Ashikhmin-Barg条件的无限族的极小三元线性码,并给出了判断极小线性码的充要条件;Ding等[9]给出了另一种判断极小二元线性码的充要条件,并构造了三类不满足Ashikhmin-Barg条件的极小二元线性码,同时确定了这些码的重量分布.2019 年,Xu 等[10]研究了奇数域上的极小线性码;Bartoli等[11]将文献[9]中的第三类极小线性码从二元推广到特征为奇数的情况.2020年,Bonini 等[12]利用文献[7]的方法构造了许多极小二元线性码;受文献[9,10]的启发,Mesnager 等[13]利用特征函数构造了多类极小线性码.
受上述工作的启发,文中基于特征函数构造极小码的方法,在文献[13]的基础上,选取适当的定义集,构造了一类具有较低重量且不满足Ashikhmin-Barg条件的极小线性码.
1 预备知识
文中总假定p是素数且q=pm,其中m是正整数;Fq是含有q个元素的有限域,F*q表示Fq的乘法群.Fp上n维空间的一个k维子空间称为码长为n、维数为k的[n,k,d]线性码C,其中最小汉明距离为d,C中的每一个向量称为码字.设Ai表示C中汉明重量为i的码字的个数,则1+A1z+A2z2+…+Anzn定义为码C的重量计数器,序列(1,A1,…,An)称为码C的重量分布.若在A1,A2,…,An中,使得Ai≠0(1≤i≤n)的个数为t,则称码C为t重码.C中码字a=(a1,a2,…,an)的支撑集定义为
supp(a)={1≤i≤n:ai≠0},
且码字a的汉明重量w(a)满足
w(a)=|supp(a)|.
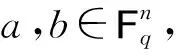
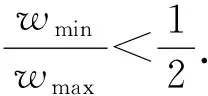
引理1[14](Ashikhmin-Barg条件) 如果Fp上的线性码C的最大汉明重量wmax和最小汉明重量wmin满足wmin/wmax>(p-1)/p,那么线性码C是极小码.
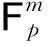
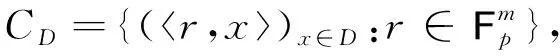
(1)
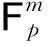

(2)
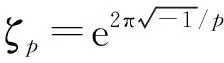

(3)

2 极小线性码的构造

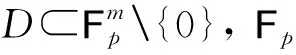
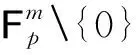
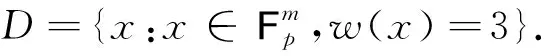
(6)
首先给出线性码CD的一些性质.
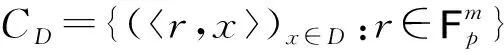
其中t=w(r).
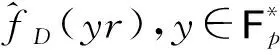
首先确定|D|,由D的定义可知


(7)
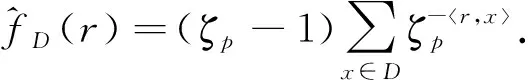
(8)
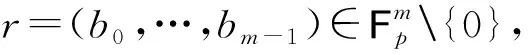
所以
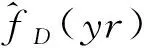
显然,w(cr)取决于w(r).所以,当给定p和m时可以确定码CD的wmin和wmax的值.可以看出,对任意的素数p及正整数m≥4,构造的码CD至多为m重的.
下面的引理3用于证明CD是极小线性码.

定理2设定义集D的选取如(6)式,则(1)式定义的线性码CD是一个极小线性码.
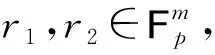
则(7)~(8)式结合引理3可知,
下证|{x∈D:r2,x≠0,r1,x=0}|>0.由线性无关可知,存在i,j使得(b1i,b2i)和(b1j,b2j)也线性无关,其中1≤i≠j≤m.因此,存在c1,c2∈Fp使得
c1(b1i,b2i)+c2(b1j,b2j)=(0,1).
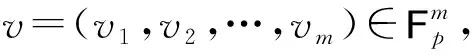
|{x∈D:r2,x≠0,r1,x=0}|>0,
即M≠(ζp-1)(p-1)|D|.因此,由引理2可知CD是极小线性码.】
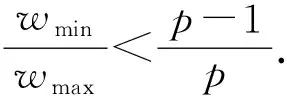
证明由引理3可知,码字cr的重量取决于w(r),从而
为了讨论方便,设w(r)=1时w(cr)的值为w1,w(r)=m时w(cr)的值为wm.下证w1 因为p为素数,所以只需(m-3)p2-3(m-2)p+3(m-1)>0. 下面对p和m的取值分类进行结论. 因此 当p=3且m≥6或p=5且m≥5时的证明与p=2且m≥6时的情形类似,此处省略. 令h1(x,m)=(m-3)x2-3(m-1)x+3m,则h1(x,m)的对称轴为 因为m为正整数,所以3/(m-3)在m=4时取得最大值4,所以x=9/2.因为p=7时h1(m,7)=31m-126,所以m≥5时h1(x,m)单调递增且均为正值.因此,当p≥7且m≥5时,结论成立. 由引理1可知,在给定参数(p,m)对的取值情形下,CD是不满足Ashikhmin-Barg条件的极小线性码,即为宽极小码.】 注1当p=2且m=3时,CD是常重码. 定理3中(p,m)特殊取值对应极小码的属性如表1所示. 表1 极小线性码的属性 在文献[13]的基础上,基于特征函数构造极小线性码的方法,通过选取适当的定义集,构造了一类不满足Ashikhmin-Barg 条件的低重极小线性码.结果表明,得到的线性码均为极小线性码,且除个别参数下的线性码属于窄极小码外,其余所得的线性码均为宽极小码,可用作设计具有良好访问结构的秘密共享方案.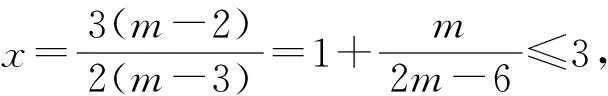
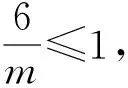
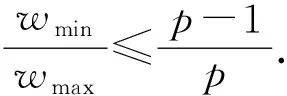

3 总结
