计及电压测量特性的MMC中高频阻抗建模及稳定性分析

李奇南，夏勇军，张晓林，孙宝奎，孙华东，张帆，李兰芳，杨岳峰，韩情涛

(1. 南瑞集团(国网电力科学研究院)有限公司, 江苏 南京 211106；2. 北京市直流输配电工程技术研究中心(中电普瑞电力工程有限公司), 北京 102200；3. 国网湖北省电力有限公司电力科学研究院, 湖北 武汉 430061；4. 中国电力科学研究院有限公司, 北京 100192；5. 中电普瑞科技有限公司, 北京 102200；6. 国网湖北省电力有限公司直流运检公司, 湖北 宜昌 443001)

0 引言

基于模块化多电平换流器(modular multilevel converter, MMC)的柔性直流输电技术 (flexible high voltage direct current, HVDC)具有无换相失败、可同时实现有功和无功的独立调节、可向无源系统供电、输出电压谐波水平低等优势[1]，在国内外得到广泛应用。中国相继建成南澳三端柔直工程[2]、舟山五端柔直工程[3]、鲁西背靠背柔直工程[4]、渝鄂柔直联网工程[5]、张北四端柔直电网工程[6]、乌东德特高压三端混合直流工程[7]，以及在建的如东海上风电柔直工程；国外建有Trans Bay柔直互联工程[8]、德国北海海上风电柔直送出工程、法国—西班牙INELFE柔直联网工程[9]等。

部分已投运的柔直工程出现了中、高频振荡现象（100 Hz～1 kHz 为中频，1 kHz 及以上为高频[10]），如鲁西柔直工程出现了1270 Hz左右的高频振荡[11]、渝鄂柔直出现了 700 Hz、1800 Hz中、高频振荡，法西INELFE出现了1700 Hz的高频振荡现象[12]。

阻抗分析法是一种有效的柔直系统稳定性分析方法，可以从机理上阐明低频、中高频振荡现象产生的原因、影响因素，为提出振荡抑制策略提供理论支撑。使用阻抗分析法进行柔直系统稳定性分析需要获取交流系统阻抗、MMC换流站阻抗。对于超（特）高压输电系统，交流系统阻抗特性较为复杂，在研究的频率范围内存在多个阻抗拐点，阻抗相位在感性、容性之间不断变化[13]。通常，交流系统阻抗通过基于交流系统详细模型等值得到。而对于MMC换流站阻抗模型，则需根据主电路参数并考虑MMC闭环控制系统作用，建立小信号（小扰动）序阻抗模型。如何建立精确的MMC小信号序阻抗模型，是应用阻抗分析法的关键。

多谐波线性化方法、谐波状态空间方法（谐波传递矩阵）是建立MMC序阻抗模型的有效方法。文献[14]采用多谐波线性化方法建立了MMC交流侧小信号正序、负序阻抗模型，该模型能够计及输出相电流控制、环流控制以及锁相环的控制作用；文献[15]建立了MMC交流侧导纳的线性分析模型，研究了在相坐标系、dq坐标系进行电流控制、锁相环对MMC交流侧导纳的影响，并通过实验验证了控制参数对导纳的影响；文献[16]采用多谐波线性化方法建立了采用双闭环定交流电压控制的MMC送端换流站小信号阻抗模型，可实现电流环对MMC阻抗影响的准确分析；文献[17-19]建立了考虑MMC频率耦合效应的阻抗模型以提高应用阻抗分析法进行柔直系统稳定性分析的准确度；文献[20-24]建立了计及控制链路延时的MMC阻抗模型用于分析中、高频振荡现象；文献[25]计及了正负序电流独立控制的影响，建立了用于柔性直流系统中、高频谐振分析的阻抗模型。

在建立MMC阻抗模型时，现有研究主要考虑了各控制环节（锁相环、电流内环、环流控制、功率外环）、控制链路延时、频率耦合效应对阻抗的影响，但并未考虑电压测量装置（电容式电压互感器）测量特性的影响。由于CVT不能准确测量电压谐波分量[26]，在分析中、高频谐振时需计及CVT谐波电压测量误差带来的影响。

1 MMC阻抗模型

基于MMC平均模型，采用多谐波线性化方法建立MMC交流侧阻抗小信号模型。本节对MMC阻抗模型建模过程进行简要介绍，详细推导过程见文献[14]。

MMC桥臂平均模型如图1所示。

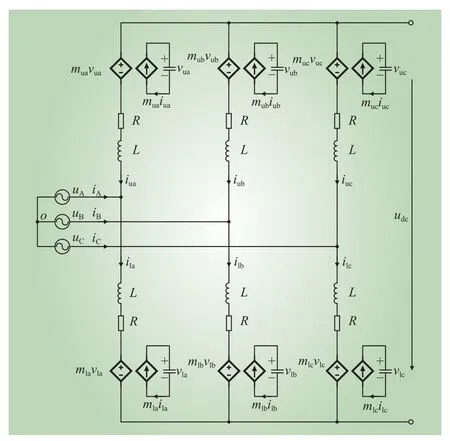
图1 MMC平均模型Fig. 1 Averaged model of MMC

对于MMC平均模型，桥臂内各子模块电容电压均一致，桥臂内各个串联的子模块用一个等值子模块表示。只考虑开关函数的低频分量，包括直流分量、基波分量以及由环流控制产生的二次分量。等值子模块交流侧、直流侧分别用受控电压源和受控电流源表示。等值子模块电容为C=Csm/N，Csm表示每个子模块的电容值，N为每个桥臂子模块数量。图1中，muj、mlj分别为MMC的j相（j=a、b、c）上、下桥臂调制波（下标u表示上桥臂，l表示下桥臂）；iuj、ilj分别为三相上、下桥臂电流；vuj、vlj分别为三相上、下桥臂等值子模块电容电压；vgj、igj分别表示MMC交流侧j相输出电压、电流；L为桥臂电感；R为桥臂电阻；udc为直流侧电压；uj、ij分别为电网三相电压、三相电流。

考虑到相间以及同相上、下桥臂电气量的对称性，MMC功率级方程基于单个桥臂建立即可。以A相上桥臂为例，MMC平均模型的功率级方程可表示为(式中省略A相下标a)

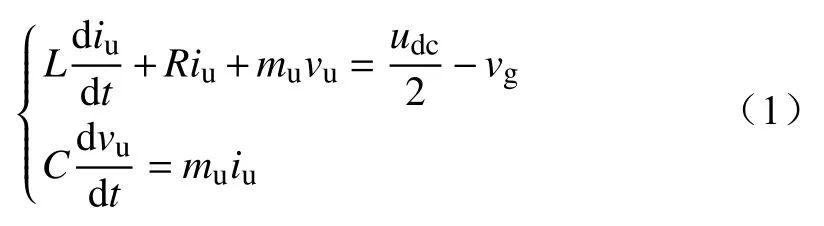
式中：mu为A相上桥臂调制波；vu为等值子模块电容电压；iu为A相上桥臂电流。

MMC平均模型为非线性。为获取小信号阻抗模型，需要将该平均模型进行线性化，并根据控制环路消去调制波（将调制波用桥臂电流、电容电压表示）。本文忽略电网电压扰动对锁相环输出、外环控制输出的影响，着重考虑定电流控制、环流控制、控制链路延时的作用。控制框图如图2所示。

图2中，id、iq分别为输出电流的d、q轴分量；id_cir、iq_cir分别为环流的d、q轴分量；ud、uq分别为M MC交流侧电压d、q轴分量；θ为电网电压不存在扰动时的锁相角；Tdelay为控制链路总延时。

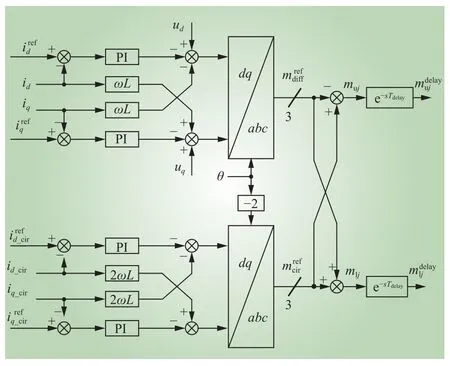
图2 MMC控制框图Fig. 2 Control block diagram of MMC

将式（1）变换至频域，在稳态工作点处通过在电网电压中注入频率为fp的正序（或负序）小信号扰动量p，并考虑控制环路作用，可得MMC闭环阻抗为式中：E为单位矩阵，Qi表示上桥臂电流扰动至差模调制波（相电流控制输出）扰动量的系数矩阵；Qv表示电网电压扰动p至差模调制波扰动量的系数矩阵；Qc表示上桥臂电流扰动量至共模调制波（环流控制输出）扰动量的系数矩阵；Zl、Zc分别为小扰动作用下，桥臂阻抗矩阵、电容阻抗矩阵；Mu、Vu、Iu分别为mu、vu、iu对应的托普利兹矩阵；Hdelay为控制链路传输延时对应的系数矩阵。各个系数矩阵中每个元素的表达式详见文献[14，23]。

2 CVT宽频测量特性

在上述MMC阻抗模型的建立过程中，未考虑CVT测量装置对中、高次谐波电压的测量误差。本节以速饱和CVT为例，分析其谐波电压传递特性。

2.1 CVT测量特性

电容式电压互感器的基本结构如图3所示。主要包括电容分压器（高压电容C1、中压电容C2）、电磁单元（补偿电感Lk、中间变压器）、阻尼单元Zd、负载（测量绕组负载Z1、计量绕组电抗器Z2）。U1N为CVT高压侧额定输入电压，U2N为CVT中间变压器一次侧额定输入电压。

图3 CVT基本结构Fig. 3 General configuration of CVT

本文以√柔直换流站中500 kV速饱和型CVT（TYD500/ 3 -0.005H）为例，计及补偿电感杂散电容Ck和中间变压器一次侧杂散电容Cs时，其宽频等值电路[27]如图4所示。

图4 CVT等值电路（计及杂散电容）Fig. 4 Equivalent circuit of CVT with stray capacitance

图4中，Lk、Rk分别为补偿电感及其电阻；Ls、Rs分别为中间变压器的漏感和电阻；Lm、Rm分别为中间变压器的激磁电感、电阻；L2、R2表示将测量绕组和计量绕组负载折算到一次侧时的负载电感和负载电阻；Ld、Rd分别为阻尼器电感、电阻；im为中间变压器激磁电流；i1、if、i2分别为中间变压器一次侧电流、阻尼支路电流和负载电流。等值电路输入电压u1=U1NC1/(C1+C2)，u2表示折算后的二次侧输出电压，Ce为等效电容（Ce=C1+C2）。

根据图4，可得计及杂散电容影响时CVT的输入电压至输出电压的传递函数为

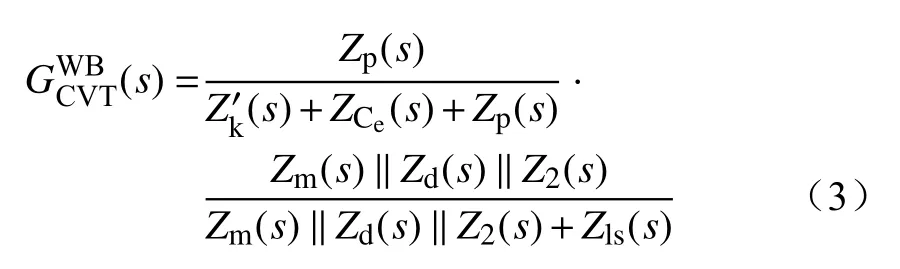
2.2 CVT宽频模型

下面简要分析Ck、Cs对CVT频率响应特性的影响。CVT 原始参数为：高压电容C1=5179 pF，C2=144338 pF，中间变压器额定电压u2N=10 kV，变比NTR=100，总负荷S=200 V·A（cosφ=0.8）。折算到一次侧的CVT等值电路参数如表1所示。

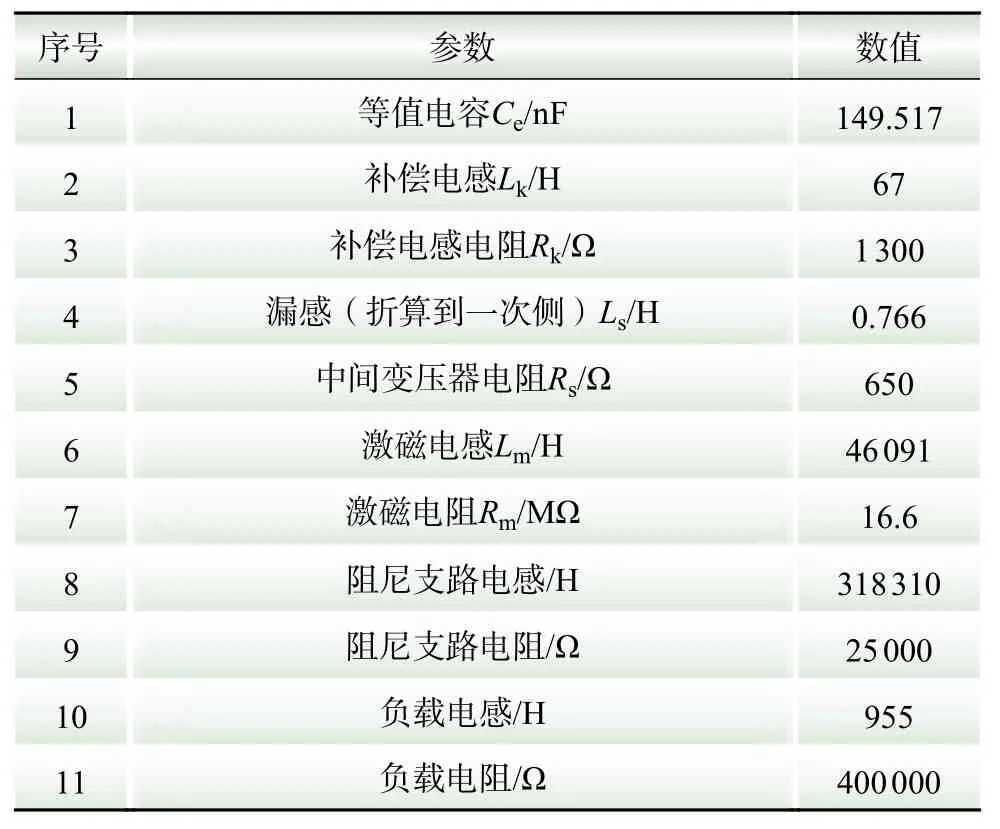
表1 500 kV CVT等值电路参数Table 1 Parameters of 500 kV CVT

当补偿电感杂散电容Ck保持不变（Ck=100 pF）、中间变压器一次侧杂散电容Cs变化时，CVT的频响曲线如图5所示。

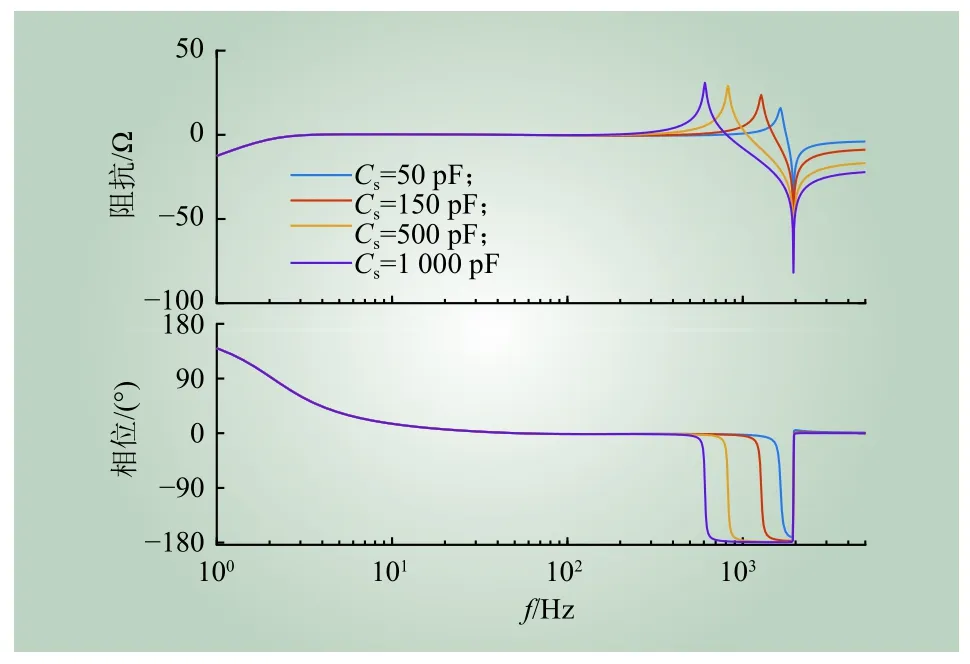
图5 速饱和型CVT随Cs变化频率特性Fig. 5 Frequency response of the fast saturated-CVT withCschanged

当中间变压器一次侧杂散电容Cs保持不变（Cs=200 pF）、补偿电感杂散电容Ck变化时，CVT的频响曲线如图6所示。

图6 Cs=200 pF时，Ck变化时CVT频率响应Fig. 6 Frequency response of the fast saturated-CVT withCkchanged（Cs=200 pF）

由图5、图6可知，杂散电容对CVT频率特性的中、高频段（700 Hz～5 kHz）有较大影响，电压幅值、相位测量值误差较大。因此，在MMC阻抗建模、系统稳定影响分析时均需考虑CVT宽频测量特性的影响。

3 计及CVT测量特性的MMC阻抗特性

由图2可知，交流电压dq轴分量ud、uq作为电流内环控制中的电压前馈项，当计及CVT交流电压测量特性时，需修正Qv系数矩阵。

3.1 Qv系数矩阵修正

当交流电压存在频率fp的扰动电压p时，CVT测量得到的扰动电压为

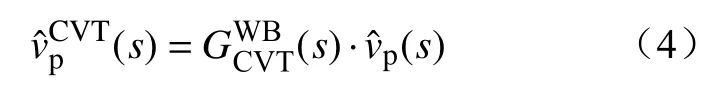
系数矩阵Qv中与扰动频率fp对应的元素位置为（k+1，k+1），该元素可表示为

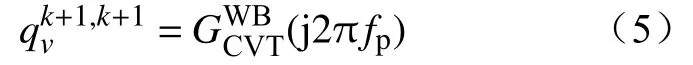
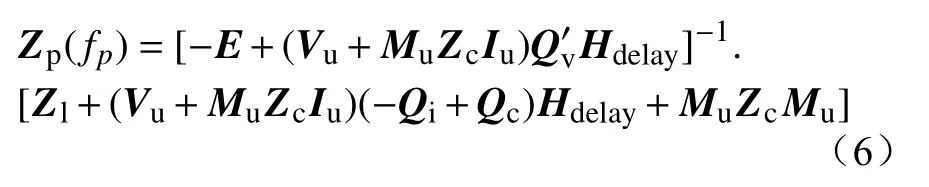
式（6）能够同时计及控制环路、控制链路延时以及CVT宽频特性的影响，适用于柔直系统稳定性分析。

3.2 阻抗特性

本文以渝鄂柔直系统（±420 kV/1250 MW）南通道MMC换流站为研究对象，MMC主电路参数及控制参数如表2所示。

表2 ±420 kV/1 250 MW MMC换流站参数Table 2 Parameters of ±420 kV/1 250 MW MMC station

以MMC工作在OLT（空载加压）模式为例，忽略外环控制，此时电流内环有功、无功电流指令分别为

考虑CVT 宽频测量特性（杂散电容取典型值：Cs=150 pF，Ck=500 pF）前后，MMC 换流站阻抗特性如图7所示。对于本算例，CVT宽频测量特性对MMC换流站中、高频阻抗特性的影响主要体现在600～840 Hz范围内。在该频率区间，MMC阻抗相位超过+90°，即阻抗实部（电阻）为负值，阻抗呈现“负电阻”特性。在806 Hz处，MMC阻抗相位最大达到163°。

图7 考虑CVT 宽频测量特性前后，MMC换流站阻抗特性Fig. 7 MMC impedance with and without CVT wide band frequency response

此外，阻抗特性在低频段（＜15 Hz）也存在差异，这是由CVT自身测量特性导致的。由图4可知，等效电容Ce的隔直作用使得CVT无法准确测量电压低频分量（见图5、图6）。本文主要考虑CVT测量特性对MMC阻抗中、高频段的影响，不再分析低频段的差异。

4 对柔直系统稳定性的影响

4.1 交流系统阻抗

交流系统阻抗采用渝鄂柔直南通道运行期间鄂侧500 kV系统等值阻抗[28]，阻抗相位在中、高频段范围内呈强容性特征。

4.2 稳定性分析

用于柔直系统稳定性分析的场景如表3所示。其中，柔直稳态运行点考虑空载、额定有功功率（整流）运行2种情况。

表3 系统稳定性分析场景设置Table 3 Scenarios for system stability analysis

应用阻抗分析法对柔直换流站运行于柔直系统在场景1～4时的阻抗特性分别如图8～11所示。

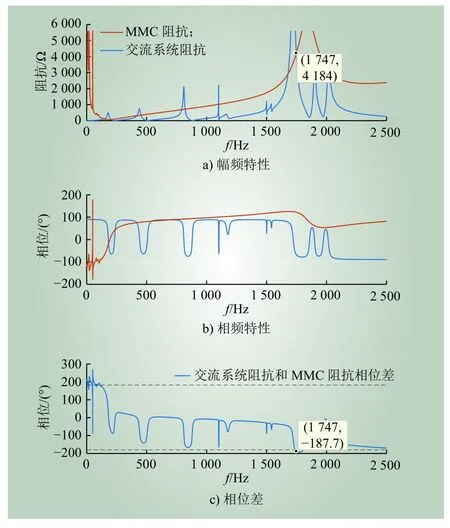
图8 MMC换流站阻抗、交流系统阻抗(场景1)Fig. 8 Impedance of MMC station and AC system(Case 1)

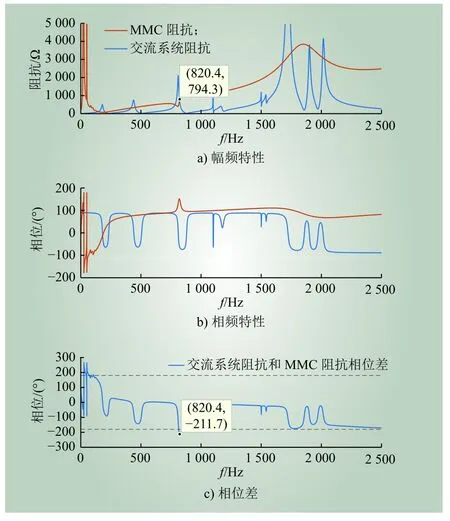
图9 MMC换流站阻抗、交流系统阻抗(场景2)Fig. 9 Impedance of MMC station and AC system (Case 2)

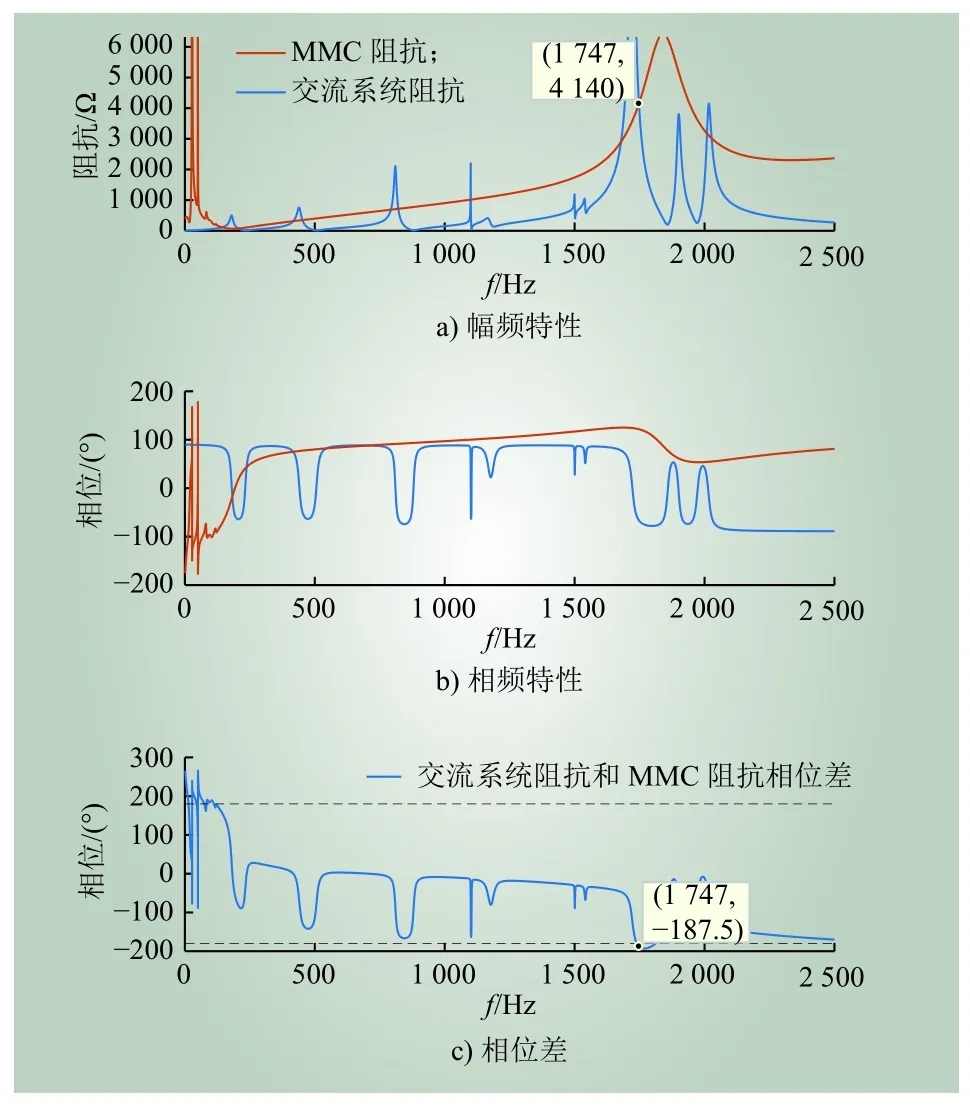
图10 MMC换流站阻抗、交流系统阻抗(场景3)Fig. 10 Impedance of MMC station and AC system(Case 3)

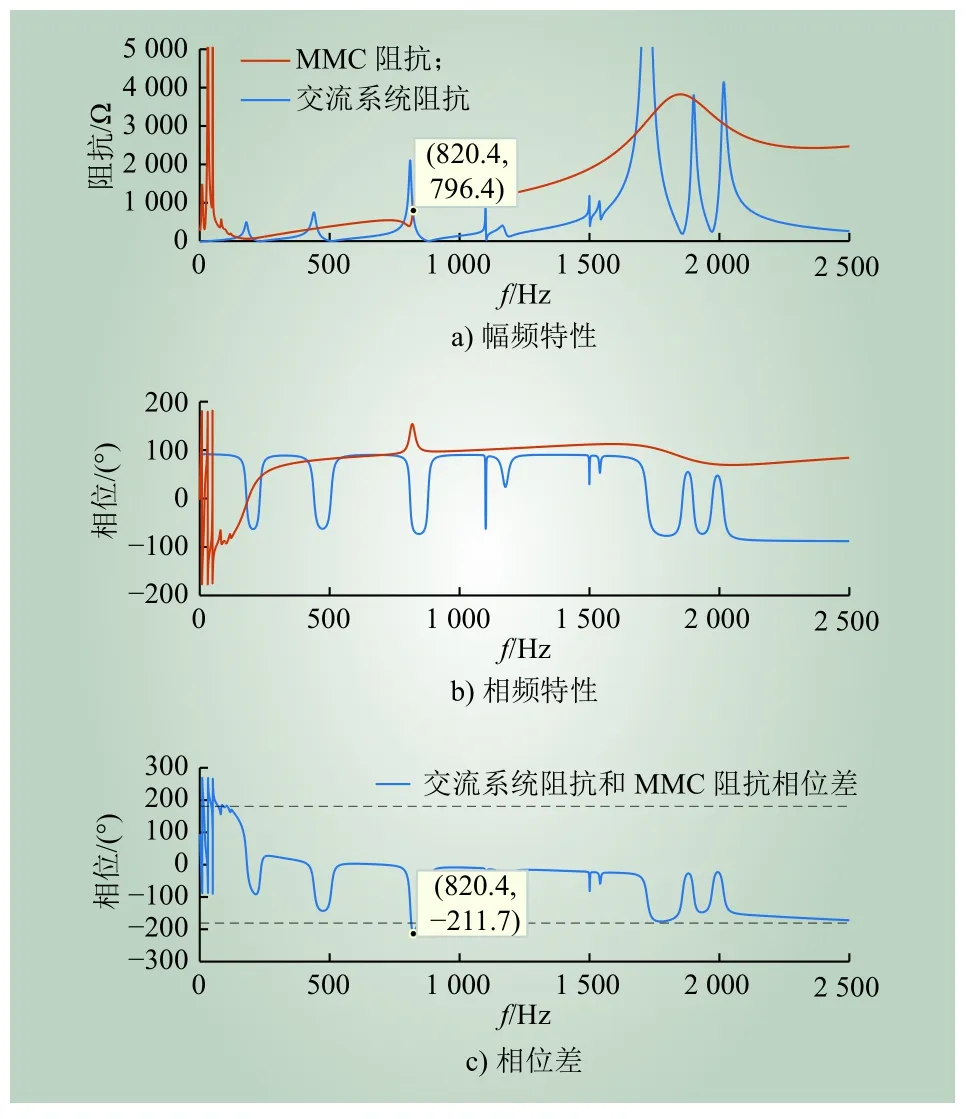
图11 MMC换流站阻抗、交流系统阻抗(场景4)Fig. 11 Impedance of MMC station and AC system( Case 4)

对于场景1，MMC换流站阻抗、交流系统阻抗幅频特性在1 747 Hz处相交，该频率处二者相频特性相位差小于−180°，为不稳定工作点。

由图9可知，CVT测量特性对MMC阻抗的影响集中在中频段（700～1 000 Hz），当计及CVT测量特性后，交流系统与MMC换流站幅频特性在820 Hz相交，该频率处二者相位差小于−180°，为不稳定工作点。

对比场景1、2可知，对于设定的交流系统阻抗，计及CVT测量特性前后系统不稳定工作点由原先的 1 747 Hz变为 820 Hz 左右。

由图10可知，与场景1相比，工作点变化对MMC换流站高频段影响不大，交流系统阻抗与MMC换流站幅频特性仍在1 747 Hz相交，该频率处二者相位差小于−180°，为不稳定工作点。

由图11可知，与场景3相比，计及CVT测量特性时，MMC阻抗中频段特性发生变化，交流系统与MMC换流站幅频特性在820 Hz相交，该频率处二者相位差小于−180°，为不稳定工作点。 不同场景下，系统稳定性分析结果如表4所示。

表4 各场景下，系统稳定性分析结果Table 4 Results of system stability analysis for each scenario

5 仿真验证

本节通过PSCAD/EMTDC电磁暂态时域仿真，验证柔直换流站运行于不同稳态工作点时，计及CVT测量特性前、后对系统稳定性的影响。

采用表2的参数，仿真步长10 μs，仿真场景与表3中的场景1～4逐一对应。图12为各场景MMC换流站并网点仿真波形。

图12 各场景并网点电压、电流仿真波形Fig. 12 Simulation waveform of voltage and current at PCC for each scenario

需要说明的是，为获得柔直系统不稳定运行时的仿真波形，仿真模型保护系统未设置谐波保护功能。而实际柔直系统在运行过程中，当并网点处电压、电流谐波含量超过设定阈值时将引起谐波保护动作，MMC换流站闭锁。

根据图12中的仿真数据进行FFT分析，可得各仿真场景下不稳定点频率，相应的谐波电压、电流幅值，如表5所示。

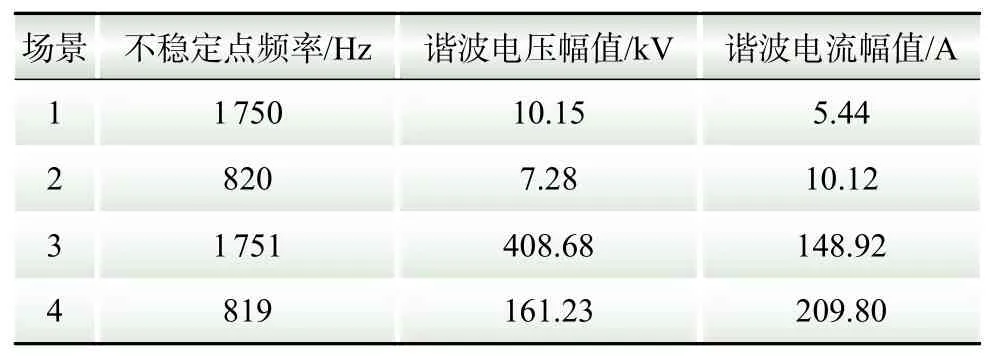
表5 各仿真场景下的系统稳定性分析结果Table 5 Results of system stability analysis for each scenario

由表5数据可知，通过电磁暂态时域仿真得到的各场景不稳定频率与第4节理论分析结果基本一致。CVT宽频测量特性可能改变系统振荡频率。

本文的研究表明，在进行柔直系统并网稳定性分析时，除需要考虑交流系统阻抗、控制链路延时外，还需计及CVT宽频测量特性对MMC换流站阻抗的影响，以提高系统稳定性分析的准确度。

6 结论

针对在现有研究建立MMC阻抗模型时未计及CVT宽频测量特性对MMC阻抗中、高频段的影响，可能会降低柔直系统稳定性分析准确度这一问题，基于多谐波线性化原理提出了一种计及CVT宽频测量特性的MMC阻抗模型建立方法。应用阻抗分析法，分析了当柔直换流站接入不同交流系统、运行于不同稳态工作点时，CVT宽频测量特性对柔直系统稳定性的影响。通过电磁暂态时域仿真，验证了理论分析的正确性。主要结论如下。

（1）CVT宽频测量特性对MMC阻抗的中、高频段特性有显著影响。具体表现在：MMC阻抗出现“负电阻”的最低频率减小，“负电阻”对应的频率范围变大，柔直系统发生谐波振荡的风险增大。

（2）对于一定的交流系统，计及CVT宽频测量特性时，将改变柔直系统振荡频率。因此，在应用阻抗分析法进行柔直系统稳定性分析时，需采用计及CVT宽频测量特性的MMC阻抗模型，以获得更为准确的分析结果。

（3)本文所提出的计及CVT宽频测量特性的MMC阻抗模型，可提高柔直系统稳定性分析的准确度，为制定振荡抑制策略、优化设计控制参数奠定基础。