问题解决测验中过程数据的特征抽取与能力评估*
2022-06-06韩雨婷刘红云
韩雨婷 肖 悦 刘红云
·研究方法(Research Method)·
问题解决测验中过程数据的特征抽取与能力评估*
韩雨婷1肖 悦2,3刘红云2,3
(1北京大学医学部全国医学教育发展中心, 北京 100191)(2应用实验心理北京市重点实验室;3北京师范大学心理学部, 北京 100875)
基于计算机的问题解决测验可以实时记录被试探索环境和解决问题时的详细行动痕迹, 并保存为过程数据。首先介绍了过程数据的分析流程, 然后从问题解决测验入手, 分别对过程数据的特征抽取和能力估计建模两方面的研究进行了梳理和评价。未来研究应注意:提高分析结果的可解释性; 特征提取时纳入更多信息; 实现更复杂问题情景下的能力评估; 注重方法的实用性; 以及融合与借鉴不同领域的分析方法。
计算机问题解决测验, 过程数据, 特征抽取, 能力评估模型
1 引言
问题解决指当问题解决者最初不知道解决问题的方法时, 为了达到特定目标而进行的认知加工过程(Mayer & Wittrock, 2006), 不论是在教育还是其他领域, 问题解决的能力都非常重要。为了帮助学生适应动态变化的社会, 培养学生跨学科的通用问题解决能力逐渐受到国内外的广泛关注(陆璟, 2017)。国际教育技术协会(International Society for Technology in Education, 简称ISTE)在2007年颁布的新版美国《国家学生教育技术标准》中将“批判性思维、问题解决与决策”列为六大能力素质维度之一(王永锋等, 2007)。我国教育部在2014年颁发了《关于全面深化课程改革落实立德树人根本任务的意见》, 首次提出要研究制订学生发展核心素养体系, 并提出要开展跨学科主题教育教学活动, 提高学生解决问题能力。
近年来, 随着对问题解决能力培养的日益关注和信息技术的快速发展, 越来越多的国际化大型评价项目开始研发基于计算机的问题解决能力测验系统。如隶属于经济合作与发展组织(Organization for Economic Co-operation and Development, OECD)的国际学生评价项目(Programme for International Student Assessment, PISA)于2012年开展了基于计算机的仿真情景问题解决测验(OECD, 2013), 于2015年添加了人机互动式的合作问题解决能力测验(OECD, 2017)。2013年, 同属OECD的国际成人能力评估项目(Programme for the International Assessment of Adult Competencies, PIAAC)测量了成人在丰富技术环境下的问题解决能力(problem- solving in technology-rich environments, PSTRE; Schleicher, 2008)。由思科、英特尔和微软发起的“21世纪能力的评价与教育”(Assessment & Teaching of 21st Century Skills, ATC21S)项目以基于计算机的人人交互形式测量了学生的合作问题解决能力(Adams et al., 2015)。美国国家教育进步技术评估项目(National Assessment of Education Progress, NAEP)的工程素养评估(Technology and Engineering Literacy assessments, TEL)中也涉及了对问题解决能力的测量(PumpRepair; TEL, 2013)。
相比于传统的纸笔测验, 基于计算机的问题解决测验可以利用信息技术建构真实的任务情境, 实现被试与测验任务的动态交互, 并且能够实时记录被试在模拟情景中的反应过程, 将其存储为过程数据(process data)。过程数据由具体任务和问题所诱发, 反映了被试解决问题所运用的能力和心智过程, 是被试潜在心理活动过程的外在表现(袁建林, 2018)。过程数据不但记录了被试的反应结果, 还记载了被试的解答步骤, 相比于传统的结果数据可以更多地揭示被试的思维过程; 过程数据蕴含了被试所使用的策略以及所犯错误等解题过程信息, 有利于区分低能力水平被试以及发现不同的错误类型, 进而诊断错误原因, 为改进教学提供针对性的建议; 过程数据可以用来还原解答过程, 识别猜测行为。总之, 过程数据对于了解被试解决问题的行为模式有重要价值。
虽然过程数据蕴含了丰富的信息, 如何利用和理解这些数据是亟待解决的问题(Mislevy, 2019)。未经计分的过程数据常常以带有时间戳的字符串行形式出现(Hao et al., 2015), 其中记录的事件可以是“单击流”这种鼠标事件, 也可以是被试为完成任务所展现的文字或图像。这种字符串行难以直接使用传统的心理测量模型进行分析, 首先需要从中提取能够反映潜在特质的特征。然而, 过程数据数量庞大, 结构复杂, 难以快速有效地从中筛选出有用的信息或指标, 加上过程数据的时序性、多维性等特征也对测量建模提出了挑战。并且, 这些行为表现是被试解决问题过程中的真实行为序列, 所有行为带有时间标签, 在时间维度上具有连续性、过程性的特点, 使用传统心理测量模型可能要面临指标之间非独立的问题。
纵观国内外这一领域的进展, 近年来研究者结合问题解决能力测评的需要, 对于如何从复杂的过程数据中获取更多关于能力估计的信息, 以及如何确立合适、准确的能力评估模型等问题进行了探讨。为了使方法学研究者更便捷地了解问题解决测验中过程数据分析的最新进展, 以及为实际应用者提供分析流程与方法选用的参考信息, 本文首先简要介绍了过程数据分析的流程; 其次, 梳理了过程数据特征抽取和能力评估模型的进展情况, 并在此基础上总结对比了不同方法的适用情景和优缺点; 最后, 结合目前过程数据分析的发展趋势, 对其未来研究方向进行了展望。
2 过程数据的分析流程
信息技术的发展使得构建复杂的计算机交互式测验成为可能, 这也激发了对于新技术环境下测验开发与表现性评定的指导理论的需求。目前, 包括PISA、ATC21S在内的大型计算机问题解决测验项目都依托“证据中心的设计”(Evidence- centered Design, ECD; Mislevy et al., 2006)理论为整体设计模型。基于ECD的测验开发与过程数据收集、分析过程可以归纳为图1所示的5个步骤, 其中“设计任务原型”和“过程数据的分析”与传统的纸笔测验区别最大。von Davier (2017)和Mislevy (2019)等都对过程数据的分析流程提出了自己的观点。
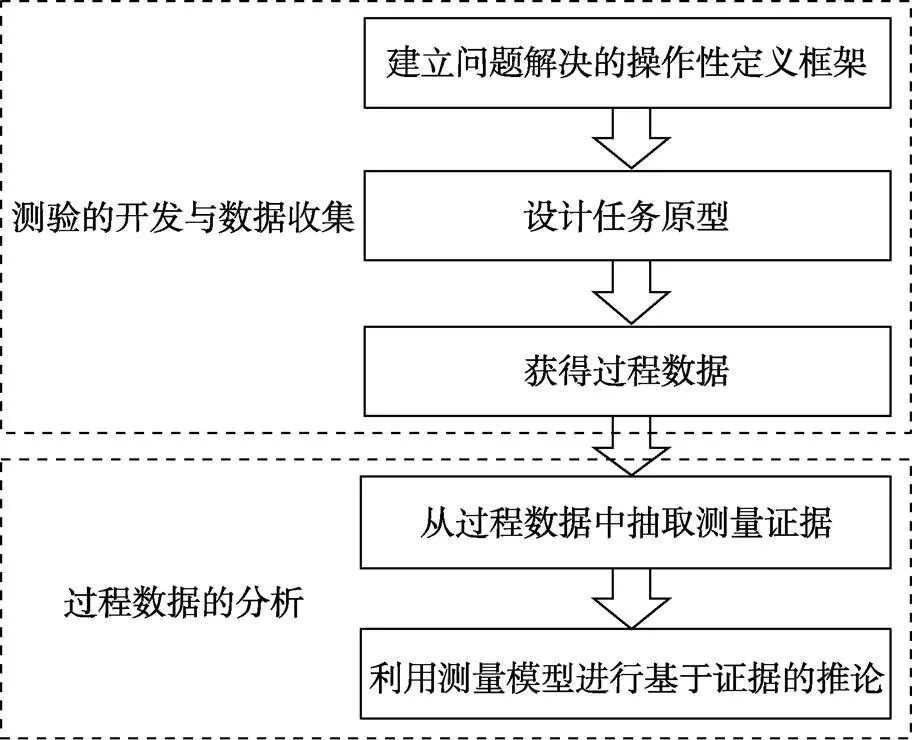
图1 基于ECD的过程数据收集与分析流程
以ECD理论为依据开发的计算机交互式测验能够以视频流、音频流和模拟日志文件的形式收集被试在问题解决过程中丰富的行为表现数据, 这些以各种形式记录的过程数据也可以统称为多模态数据。对多模态数据进行处理和分析, 可以研究和理解个人和群体层面的表现(Amer et al., 2014; Morency et al., 2010; Siddiquie et al., 2013)。von Davier (2017)在多模态层次方法(multimodal hierarchical approach; Khan, 2017; Khan et al., 2013)的基础上总结了一种适用于计算机交互式测验中非结构化数据的分析框架——计算心理测量学(Computational psychometrics), 它将计算机科学领域的数据驱动的研究方法(特别是机器学习和数据挖掘)、随机过程理论和理论驱动的心理测量学相整合, 以便实时测量潜在能力。其基本思想如图2所示:首先以ECD理论为原则开发项目, 进行测试, 并将多模态数据(过程数据)与传统的测验项目数据(结果数据)一起收集, 测验开发与数据收集程序依赖于人类专家系统的理论输入, 是一个自上而下的过程; 然后使用数据挖掘(data mining, DM)和机器学习(machine learning, ML)等算法对多模态数据进行特征抽取(Feature extraction)和表征(Representations), 如果确定了新的行为表现特征, 则可以考虑将其纳入之后的心理测量模型建构中(von Davier, 2017); 接下来, 更新测量模型, 并采用新的样本重复这一过程, 如果数据允许也可以使用随机过程模型, 循环以上过程直到测量模型稳定。

图2 计算心理测量学(改编自von Davier, 2017)
Mislevy (2019)认为两个基本的分析过程有助于解释和建模过程数据。第一是描述给定行为表现中的证据, 也就是说, 从复杂多样的过程数据中提取有用的信息(证据), 这类似于人类评分员在评估被试的复杂表现时其大脑中隐藏的过程。除了专家指定提取规则外, 这一分析程序也可以借助于数据挖掘、知识工程(knowledge engineering)和计算语言学(computational linguistics)等技术完成(Bejar et al., 2016)。第二是测量建模。在基于计算机的测验中, 我们可以追踪、积累和综合行为表现过程中的证据, 并构建目标构念(construct)的操作化变量。这些行为表现特征依赖于被试的潜在特征, 它们之间的概率关系可以被测量模型所建构。
综合以上观点, 对于计算机问题解决测验中过程数据的分析包含了两个主要步骤:从过程数据中抽取有关被试潜在能力的可解释信息, 以及利用抽取的信息对被试的能力进行估计。在信息提取阶段, 分别有依赖于专家的自上而下的方式, 和数据驱动的自下而上的方式; 而在能力估计阶段, 可以采用传统的心理测量学模型, 若数据允许, 也可以选择随机过程模型。以下分别对过程数据分析的这两个核心步骤——特征抽取和能力评估的最新研究进展进行梳理与总结。
3 过程数据的特征抽取方法
目前从问题解决测验过程数据中抽取关键特征或有意义的行为指标的方法主要有理论驱动(自上而下)和数据驱动(自下而上)两种方式。
3.1 自上而下的特征抽取方法
自上而下的特征抽取方法指以问题解决的概念框架为基础, 结合具体任务, 由专家制定从过程数据中寻找与问题解决构念元素相关联的有意义行为模式的过程, 具体过程如图3所示:专家组在测验概念框架的基础上, 针对每一个具体的任务情景, 都要基于构念内涵规定其操作性定义以及在任务中可能的表现水平, 并以此制定详细的过程指标提取及赋值规则。一般需组织多位专家进行行为指标的设计、评审和修改的迭代工作。在确定了指标提取规则后, 还需要将其转换为程序算法, 以实现过程数据的自动化抽取。为了确保行为指标及其赋值规则的有效性, 在指标规则编写阶段需要专家组非常清晰地理解被试在作答过程中的认知过程; 在使用自动化程序获得被试过程数据的指标得分后, 还应组织领域专家对提取的指标进行打分, 并对评分者之间以及自动化评分结果之间的一致性程度进行检验, 一致性程度可以采用Kappa系数来衡量。

图3 自上而下的特征提取流程
这种方式是目前国际大型问题解决测验系统的主流评分方式。PISA 2012问题解决测验, ATC21S项目的合作问题解决测验(Adams et al., 2015), NAEP-TEL测验(Shu et al., 2017)等都采用了专家定义的过程数据指标提取与计分方法。在其它一些涉及过程数据分析的研究中, 研究者也针对不同任务制定了相应的过程数据编码计分规则(如Harding et al., 2017; Rosen, 2017; Yuan et al., 2019; Zoanetti, 2010; 袁建林, 2018)。然而, 自上而下的方式需要专家组为每个具体任务制定特定的评分规则, 即存在任务特异性问题, 且成本很高。
3.2 自下而上的特征抽取方法
为了解决理论驱动方法的任务特异性问题, 有研究者尝试采用数据驱动的方法直接从过程数据记录的反应序列中提取信息。这类方式目前尚处于初步探索阶段, 并没有形成统一的分析范式, 大多数方法都是借鉴其他领域的现有算法。根据这些方法的处理思想和来源领域, 可以将自下而上的过程数据特征抽取方法分为以下三类:将反应序列类比于字符串行, 借用自然语言处理(Natural Language Processing, NLP)技术由反应序列建构指标的方法(He et al., 2021; He & von Davier, 2016); 使用降维算法构造反应序列的低维数字特征向量的方法(Tang, Wang, et al., 2021; Tang et al., 2020); 以及使用有向图表征反应序列, 并使用网络指标表征反应特征的方法(Vista et al., 2017; Zhu et al., 2016)。
3.2.1 基于自然语言处理的特征抽取方法
过程数据中记录的行为操作序列可以被编码为带有时间戳的字符串序列(Hao et al., 2015), 如“开始, 操作1, 操作2, 操作3, 结束”, 因此有研究者提出可以将操作序列类比于自然语言中的字词, 使用NLP领域的分析方法从中提取信息, 目前采用的技术主要有N-Gram, 编辑距离(edit distance)和基于最大公共子序列(Longest Common Subsequence, LCS)的指标这几种方法。
N-Gram是一种基于统计语言模型的算法, 它对文本中长度为的字符序列进行提取, 并对每个短序列进行统计, 过滤掉低频序列后, 形成文本的向量特征空间, 每一个短序列就是一个特征向量维度。将N-Gram应用于过程数据即提取反应序列中长度为的操作序列并统计, 有研究者据此识别关键操作序列, 如He和von Davier (2016)采用N-Gram对PIAAC问题解决题目中的反应序列进行表征, 并以频率−逆序列(term frequency and inverse sequence frequency, TF-ISF)加权, 获得每种操作序列的特征向量, 然后以被试作答的最终结果分组, 使用卡方检验识别出与成功解决问题相关的关键操作序列。还有研究者为提取的N-Gram赋予认知含义, 以进一步用于测量建模, 如李美娟(2020)在使用N-Gram识别出关键短操作序列的基础上, 进一步组织专家为其赋予认知含义, 以此定义合作问题解决任务中的行为指标。Zhan和Qiao (2020)直接为过程中的短操作序列(N-Gram)赋予认知含义, 用于诊断分类分析。利用N-Gram提取操作短序列的方法计算简单, 容易实现, 还可以经由专家定义构造行为指标。然而, N-Gram假设第个操作的出现只与前面−1个操作相关, 与其它任何操作都不相关, 因此该方法尽管考虑了相邻的操作, 仍丢失了操作序列中的大部分顺序信息。并且, 采用这种方式得到的特征向量维度数等于所有N-Gram的总数, 当可采取的行为数量较多时, 维度数将非常庞大。此外, N-Gram还依赖于反应序列的记录方式, 一旦反应序列的编码方式发生改变, N-Gram的形式与数量也会受到影响。
对于已知最佳表现对应的操作序列的测验任务, 很容易想到直接根据被试的作答序列与最佳作答序列的相似程度来评价被试的表现, 目前已有研究者借用NLP中的编辑距离和最大公共子序列(LCS)来衡量它们之间的相似度/差异。编辑距离又称Levenshtein距离, 指两个字符串之间, 通过替换、插入或删除字符的编辑操作, 由一个转成另一个所需的最少编辑次数(Levenshtein, 1966)。两个字符串之间的距离越大, 说明它们越不同。Zhan等(2015)通过比较被试在NAEP-TEL泵修理任务(PumpRepair; TEL, 2013)中的操作序列与最佳序列之间的Levenshtein距离衡量了他们的表现。最大公共子序列指两个给定字符串的最长公共部分, He等(2021)基于被试反应序列和最佳反应序列的LCS构建了评估反应序列相似性(Similarity)和有效性(Efficiency)的指标。利用被试的作答序列与最佳序列的距离/相似程度来构造行为指标的方法同样计算简单、容易实现, 并且指标含义明确, 易于理解。然而这些指标也依赖于编码形式, 并且其高度概括性会导致过程数据中很多有用信息的丢失, 使其难以区分不同的行为模式。
3.2.2 使用降维算法获得操作序列的低维表征
为了提取反应序列中的所有过程信息, 有研究者提出使用降维算法, 如自编码器(autoencoder)和多维尺度分析(multidimensional scaling, MDS), 获取反应序列的数字特征向量, 所提取的数字向量可用来预测被试的表现或提高能力估计精度。


3.2.3 借助网络指标描述反应过程特征的方法
社会网络分析(Social Network Analysis, SNA)可以通过对关系数据的系统分析来考察关系结构及其网络的特征(徐伟等, 2011)。过程数据中记录的反应序列不是独立活动的集合, 它们蕴含了被试在解决问题时候的活动顺序, 使用有向图可以直观地展现反应的变化过程, 进而可以使用SNA指标对反应过程的特征进行描述。有向图可以表征个体的操作序列也可表征群体的反应过程。如Zhu等(2016)根据每位被试在NAEP-TEL泵修理任务中的反应序列构造了表现操作之间相互依存关系的加权有向图(Wasserman & Faust, 1994)。而Vista等(2017)将任务状态和被试的对话事件作为网络节点, 事件之间的先后顺序作为连线, 分别对ATC21S的橄榄油()任务中的高能力组和低能力组构造了被试群体的网络图。可以用来刻画反应过程网络的特征指标有度(density)、中心化(centralization)、描述局部模式特征的互惠二元体(reciprocity)和三元体(triad census; Davis & Leinhardt, 1972; Wasserman & Faust, 1994)、突出(prominence)、分支(branches)、集群(clusters)和最短路径(shortest paths; Vista et al., 2017)等。不同成绩/能力的被试/被试群体的反应过程网络指标存在差异(Zhu et al., 2016; Vista et al., 2017), 对被试表现有一定的预测作用。
此类方法的特点是将反应序列视为一个整体过程, 而不是关注单个事件。使用网络图表征反应序列可以直观地呈现反应模式, 进而可以使用SNA指标描述反应过程的特征。该方法面临的主要挑战之一是数据的复杂性, 需要大量的数据清理与预处理。另一方面, 使用SNA指标描述反应过程有向图的特征时, 只能获取网络的结构特征, 丢失了反应顺序信息, 而且无法捕获节点的内容信息, 也损失了具体反应类型的信息, 难以用来对被试的表现水平进行进一步推断。
3.3 特征提取方法简评
综上所述, 采用自上而下方式定义的行为指标与概念框架有紧密的对应关系, 具备可解释性和明确的得分, 可以如传统测验中的题目一般, 直接利用心理测量模型分析, 获得被试的潜在能力估计值。然而, 此类指标建构方法的工作量巨大。特别的, 在复杂任务中, 专家可能遗漏或忽视未知的、以往未被关注的学生思维过程, 从而造成信息的遗漏和损失。
数据驱动的自下而上的特征抽取方式部分解决了专家建立评分规则的任务特异性问题, 所提取的特征可用于探索不同被试群体的行为模式特点, 预测被试在未来的表现, 在经专家定义后也可被用来进行能力估计, 对于测试和任务开发以及评分规则的改进方面都有一定价值。然而, 这类方法也不一定能保留过程数据中所有的信息, 并且所获得的指标与所测心理特质之间的关联并不明确。本文根据来源领域和处理思想将问题解决中自下而上的过程数据特征抽取方法分为三大类, 经过上述介绍可以发现, 这三类方法在信息利用上各存在一些局限性。如借用NLP构建指标的方法依赖原始编码, 且指标大多过于笼统, 信息损失大, 其中编辑距离和基于LCS的方法仅适用于存在最佳解决方案的任务情景, N-gram方法也仅适用于可执行操作较少的任务; 使用降维算法获取的反应过程数字表征, 保留了整个反应序列的信息, 可以用于预测分析, 也有研究提出了利用此类过程信息的能力估计模型(Zhang et al., 2020), 但此类方法抽取的特征缺乏可解释性。最后, 使用网络指标描述反应过程特征的方法可以对反应过程可视化, 并且用于探索不同群体的反应模式特点, 但该类方法难以捕获具体操作信息, 且抽取的特征无法直接用于被试能力的估计。因此, 数据驱动的特征抽取方法同样可能面临信息遗漏的问题, 且具有可解释性问题, 利用此类特征进行能力估计的研究非常少, 因此纯粹数据驱动的特征抽取方法尚未直接应用于大规模标准化测试的能力评估中。各种特征抽取方法的特点可以归纳如表1。
4 过程数据能力评估模型
在从过程数据中抽取出行为指标/特征后, 需要构建它们与潜在能力之间的概率关系模型, 以实现对能力的估计。根据模型是否利用了指标之间的顺序关系, 以及能否获得连续可解释的潜在能力估计值, 可以将目前利用过程信息估计潜在能力的方法分为以下三类:传统心理测量模型及其拓展模型, 随机过程模型, 以及结合了随机过程思想的测量模型。
4.1 传统心理测量模型及其拓展
由专家定义获得的行为指标直接对应于测验概念框架中的构念元素, 可以类比于传统测验中的题目拟合测量模型。针对多维的测验结构, 可以使用多维IRT模型和诊断分类模型同时估计多个维度上的能力或者诊断多个技能的掌握程度(e.g., Hesse et al., 2015; Siddiq et al., 2017; Yuan et al., 2019; Zhan & Qiao, 2020); 若测验以小组形式进行, 还可以拟合多水平模型(Wilson et al., 2017)。除了直接采用现有的心理测量模型进行分析, 也有研究者根据过程数据的特点对传统测量模型或其评估步骤进行了拓展(李美娟等, 2020; Liu et al., 2018; Zhang et al., 2020)。
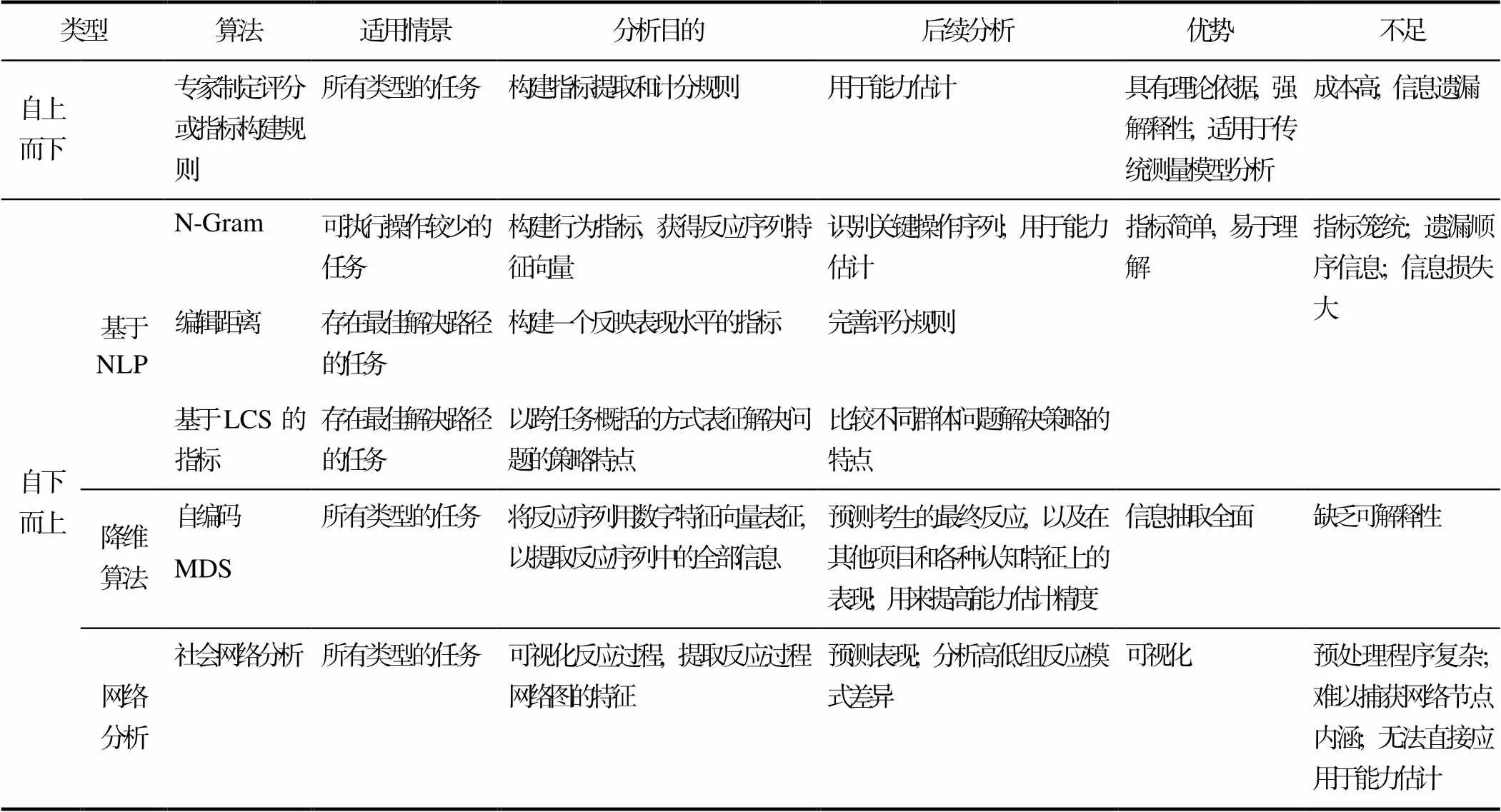
表1 基于计算机的问题解决测验过程数据的特征抽取方法总结
4.1.1 多维IRT模型
当从过程数据中提取的行为指标对应于问题解决操作性概念框架中的多个元素/子维度时(Hesse et al., 2015; OECD, 2013; Rosen, 2017), 可以采用多维IRT模型对被试在多个子维度上的表现水平进行估计。如有研究采用多维随机系数多项logit模型(Multidimensional Random Coefficients Multinomial Logit Model, MRCMLM; Adams et al., 1997)对ATC21S的多项合作问题解决测验的行为指标进行了分析, 获得了被试小组在多个维度上的能力估计值, 并且发现使用多维IRT模型的拟合效果要好于使用单维IRT模型对几个维度分开估计时(Hesse et al., 2015; Siddiq et al., 2017)。指标的多维性除了对应于目标能力的多个子维度外, 还可以对应于合作解决问题小组内的不同成员。Yuan等(2019)在分析一个以两人小组为测试单元的“人人交互”模式的合作问题解决测验时, 将抽取的行为指标按照实施主体区分为被试个体的和小组共同的, 使用项目内多维的MRCML模型分析, 实现了对个体的表现以及小组内成员间影响强度的估计。
4.1.2 多水平(多维)IRT模型

4.1.3 诊断分类模型
诊断分类模型(diagnostic classification models, DCM)是一类对几个细粒度离散潜在属性和观察到的项目反应之间的关系进行建模的限制性或验证性潜在类别心理测量模型(von Davier & Lee, 2019)。Zhan和Qiao (2020)提出了一种将诊断分类融入过程数据分析的方法:将反应序列中的相邻短操作序列(N-Gram)视为过程项目, 并以其是否出现转换为0-1编码; 然后以产生这些操作序列所需的问题解决技能为潜在属性, 给过程项目标定Q矩阵; 最后使用高阶诊断分类模型进行分析。使用高阶DCM分析过程数据可以在评估被试连续的潜在问题解决能力的同时, 根据被试的问题解决策略对其进行分类, 然而使用N-Gram构建二分编码的过程指标, 丢失了反应序列的整体先后顺序以及N-Gram的频率信息; 此外, 在更加复杂的任务中, 由N-Gram构建的过程项目数量庞大, 其Q矩阵标定的成本非常高。
上述这些研究都是现有心理测量模型在分析过程指标上的新尝试, 没有对模型本身提出改进, 且都需要专家明确定义行为指标与测量构念间的关系。
4.1.3 改进的多水平混合IRT模型
为了在考虑过程数据嵌套性质的基础上, 同时探讨被试反应过程中采取的不同策略, Liu等(2018)对多水平混合项目反应理论模型(Multilevel Mixture Item Response Theory, MMixIRT; Cho & Cohen, 2010)进行了拓展, 提出适用于处理过程数据的改进的多水平混合IRT (modified MMixIRT, mMMixIRT)模型。该方法首先穷举了任务中的所有操作, 并事先判定各个操作的正误。在过程水平上, 将所有操作的累计信息(计分)作为特定步骤的过程数据; 在个体水平上, mMMixIRT可以自定义设计矩阵A以决定个体层面能力估计所用到的信息, 比MMixIRT模型设定更灵活。mMMixIRT不仅可以在过程水平分析反应策略类别特征, 还可以同时估计出过程水平和个体水平上的能力值。为了避免mMMixIRT模型中各潜在类别内能力正态分布的前提假设难以满足的问题, 李美娟等(2020)在mMMixIRT模型基础上做了进一步的修正, 在过程水平上仅区分策略类别, 不再估计过程能力。这种穷举式的计分方式使得mMMixIRT模型利用了被试在解答过程中每一步的作答数据, 但这种特殊编码方式也具有任务特异性的问题, 并且mMMixIRT模型对被试水平的能力估计是根据被试在最后一步上的作答得到的, 即并未包含过程中的顺序信息。
4.1.5 两步条件期望方法
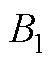

图4 两步条件期望法构造潜在特质估计值的流程图(Zhang et al., 2020)
4.2 随机过程模型
在问题解决测验或类似平台中, 被试解决任务的步骤可以被视为沿着离散时间点的连续反应过程, 过程中的反应序列相互依赖(Bellman, 1957; Puterman, 1994)。因此可以采用描述随机过程的概率模型对前后依赖的过程指标进行拟合, 并获得每个时刻上的潜在状态水平——可能对应于被试随时间变化的知识掌握状态或能力表现水平。常用的随机过程分析方法主要有隐马尔可夫模型(Hidden Markov Model, HMM)和动态贝叶斯网络(Dynamic Bayesian Network, DBN)。
4.2.1 隐马尔可夫模型
HMM是关于时序的概率模型, 描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列, 再由每个状态生成一个观测而产生一个观测随机序列的过程(李航, 2012)。HMM已经被用于分析自适应同伴辅导系统和自适应测试中的过程数据(Arieli-Attali et al., 2019; Bergner et al., 2017)。HMM还可以被用来拟合被试在问题解决测验或类似系统中的观察序列, 并得到各个时间点上的潜在状态水平。Xiao等(2021)使用HMM分析了PIAAC 2012两个问题解决项目的动作序列, 识别出潜在状态和状态之间的转换, 结果发现在两个项目中, 作答正确的被试都更专注于任务, 且更经常使用有效的工具来解决问题, 而作答错误者则更有可能使用较短的动作序列并表现出犹豫的行为。由此可以看出, 基于数据驱动的 HMM 方法可以帮助研究者更好地理解被试在复杂问题解决任务中表现出的动作序列背后的行为模式和认知转换。
4.2.2 动态贝叶斯网络
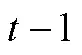
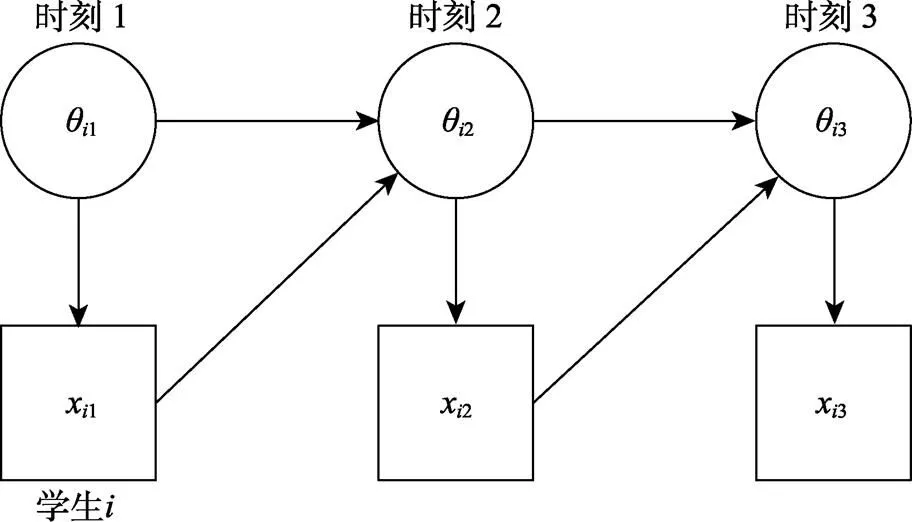
图5 一个DBN的路径图 (Levy & Mislevy, 2016, page 384)
Levy (2019)结合DBN、认知诊断建模和过程数据分析方法, 分析了一款针对有理数加法的教育游戏(Chung et al., 2010)的数据。游戏包含23个难度依次递增的关卡, 每个关卡有若干种观测反应类型, 每种反应类型被指定对应于若干种潜在技能。Levy (2019)使用DBN对观测序列进行分析, 得到了每名被试在整个游戏过程中每次尝试所对应的各个潜在技能的掌握程度或对错误观念的持有程度等结果。
DBN可以利用不同模式的反应序列信息, 保持反应序列的序列结构; 使用潜在状态对不同的潜在特质和技能建模, 从而实现认知诊断。无论HMM还是DBN, 分析得到的都是随着过程变化的离散的知识掌握状态或能力状态。然而, 有别于智能辅导测验的是, 在心理测验中, 研究者一般想要得到的是被试稳定、连续的能力估计值。这些条件限制了DBN在现代评估环境下利用反应过程数据对被试潜在能力评估的应用。
4.3 结合随机过程思想的测量模型
被试在问题解决测验中的反应过程部分处于被试的控制之下, 即被试决定在特定状态下采取什么步骤, 因此, 在给定潜在能力的条件下, 每个被试的反应过程都可以被视为一个具有条件一阶马尔可夫特性的离散时间的随机过程(Shu et al., 2017)。为了在建模时保留反应过程指标间的顺序关系, 同时从中获得连续的潜在能力估计值, 有研究者提出了结合随机过程思想的测量模型。
4.3.1 马尔可夫IRT模型


4.3.2 连续时间动态选择模型
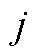
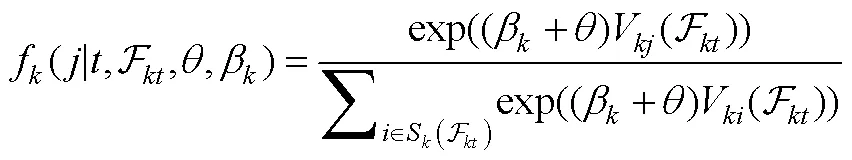
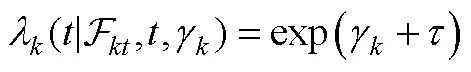
4.3.3 马尔可夫决策过程测量模型

4.3.4 序列反应模型
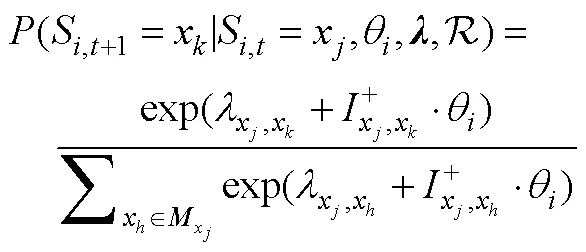
4.3.5 结合随机过程思想的测量模型总结

4.4 对当前过程数据能力评估模型的整体评价
综上所述, 要想利用能力评估模型由观测指标估计潜在能力水平, 合理建构指标与潜在能力之间对应关系是必不可少的, 如“3过程数据的特征抽取方法”部分所述, 目前这一过程仍需借助专家经验(无论是分析前还是分析后)。不同种类评估模型的可解释性依赖于它们利用的指标与潜在结构之间的假设强弱。心理测量模型重点关注潜在能力的估计, 除了传统测量模型的直接应用, 也有研究者对现有模型或估计步骤提出了改进。此类模型使用的过程指标一般与潜在能力之间有比较强的对应关系, 分析结果可解释性强(两步条件期望法除外), 但受限于局部独立性假设, 分析时不包含指标之间的顺序信息。随机过程模型关注对反应过程的建模, 保留了反应路径信息, 但指标与潜在结构之间的假设较弱, 有时先采用数据驱动模型获得潜在状态水平再进行理论解释, 且不关注稳定而连续的潜在能力估计值。在使用教育和心理测验对被试的知识、技能和能力等特质进行测量时, 最主要的目的是得到被试潜在特质的有效估计值。从这一点来看, 随机过程模型很难满足教育和心理测验对稳定连续的能力特质进行有效估计的需要。最后, 结合了随机过程思想的心理测量模型兼具两者优点, 分析对象为任务中的行动序列, 可以保留行动的先后顺序, 且由专家规定与能力方向相同的指标系数或计分方式, 具有一定可解释性, 因而可以利用比较完整的反应过程信息获得连续的潜在能力估计值。但此类模型需要穷举任务中的所有行动, 多适用于操作集有限的简单任务。因此, 如何充分利用反应过程信息, 更准确地评估被试的潜在能力, 同时兼具分析结果的科学合理和可解释性, 还有进一步研究的空间。各个模型的适用情景, 优缺点以及研究中使用的实际数据集和分析软件工具汇总于表2。
5 问题与展望
为了利用基于计算机的问题解决测验获得有效的能力估计值, 科学合理地分析过程数据是必不可少的。对于过程数据的分析一般分为特征抽取和能力评估模型建构这两部分, 本文介绍了这两方面最新的方法学研究, 并对每种方法的适用情景、优缺点进行了总结, 可以为方法学研究者快速掌握问题解决测验中过程数据分析方法的新进展提供参考, 以促进方法学上的创新, 还可以为实际应用者在分析数据时选择恰当的方法提供参考, 对后续研究的展开有指导意义。目前关于如何提取过程数据特征和利用过程数据评估被试的潜在能力这一议题的研究仍处于初始阶段, 基于前文总结, 存在以下几个可以改进的方面。
5.1 对过程数据进行分析时的可解释性问题
在对过程数据进行分析的各个阶段保证心理学层面的可解释性是一项值得关注的话题, 对保证测验结果的公正性、有效性和客观性有重要意义。在对过程数据进行特征提取时, 利用自下而上的方式可以直接获得反应序列或关键特征的数字表征, 然而这些指标与目标心理变量间的关联机制却相对难以解释和理解。在对过程指标建模时, 应保证估计得到的潜在能力水平与所测量的潜在构念水平相匹配。研究人员在对过程数据进行分析时, 应遵从ECD理论“基于证据的推理”理念, 在提取证据时应结合心理学理论, 关注证据指标的心理学含义, 并尝试使用解释性强的算法进行建模。此外, 若想利用过程数据深入探究问题解决的认知加工过程, 仍需要测验开发者、领域专家和心理测量专家共同参与决定。对于错误策略的区分与解释, 可以首先由自下而上的方式提取出蕴含错误信息的特征, 再进行聚类分析, 不同的特征组合可能反映了不同的策略类型, 但聚类结果仍需专家解读。
5.2 过程数据的特征提取应纳入更多信息
在保证所提取特征的可解释性的同时, 应该尽可能多地从过程数据中抽取有价值的信息。当前对于过程数据的利用大多基于行为表现信息, 只有少部分研究利用了过程数据中记录的时间或语言信息(Chen, 2020; 袁建林, 2018), 未来研究应考虑如何将这些行为表现以外的多模态信息纳入到测量模型中, 以对能力进行更准确的估计。此外, 为了应用于大规模标准化测验, 无论哪种信息提取方式, 都应能实现信息(指标)的自动提取与评分, 对于多模态数据的指标自动提取与合理评分也有具有一定的挑战性。
5.3 实现更复杂问题情景下的能力评估
当前的随机过程以及结合了随机过程思想的测量模型都假设在给定被试潜在能力的条件下, 被试的反应过程具有(条件)一阶马尔可夫性质。这在简单的测验情境中是成立的, 但是在一些复杂的反馈较多的动态问题情境中, 有条件的一阶马尔可夫性质可能被违背。从表2“实证数据集”可以看出, 目前可供研究者使用的实证数据集并不丰富, 大多集中于PISA、PIAAC和ATC21S这三个大型测验项目。特别地, PISA问题解决测验“车票”题的使用频率较高, 主要因为这道题的题型结构简单。这也从侧面反映出当前模型在分析复杂任务时的局限性。因此, 在提出开发更多更复杂测验需求的同时, 方法研究者也应提供相应的数据分析处理方法。此外, 过程性测验中也可能存在影响被试表现的协变量, 如有研究表明问题解决坚持性和开放性等因素会显著影响学生数字化环境中的问题解决能力测验上的成绩(袁建林等, 2016)。未来研究还可以考虑构建适用于过程数据的包含协变量的评估模型, 以进一步提高能力估计精度。
5.4 从理论研究走向实际应用
对于过程数据分析方法的理论研究需要实践检验其实际效能。一方面, 无论分析方法使用了多么复杂的测量模型或者数据挖掘技术, 最终都应服务于实际。从表2的最后一列可以看出, 大部分现有评估模型都有相应的参数估计软件或软件包可以实现参数估计, 但是对于针对过程数据开发的新模型, 则可能需要自编程序实现参数估计, 这使得模型应用门槛较高。因此应鼓励新模型的开发者公开参数估计代码, 或开发简单易上手的软件包, 以便模型的使用与推广。另一方面, 为了方便实际应用者, 测验开发者还可以考虑如何在现有分析方法的基础上, 开发用户友好的问题解决测试系统, 实现过程数据的自动评分、能力评估结果以及知识技能诊断报告的即时生成等功能。
5.5 不同领域分析方法间的融合与借鉴
本文聚焦于梳理问题解决测验的特征抽取与能力评估研究, 目前特征提取的方法和能力评估模型之间并非完全匹配, 大多数以数据驱动方式抽取的特征由于没有建立与潜在能力之间的对应关系, 可能仅适用于聚类和预测等分析目标, 而无法应用于能力评估模型中。而心理测验的主要目的就是对被试的潜在能力进行准确的测量, 研究者应开发更多可以应用于能力评估模型的特征提取方式。此外, 除了问题解决能力, 对于许多其它高阶能力的测量也初步实现了计算机化, 如批判性思维(Liu et al., 2016; Song & Sparks, 2019)、创造性思维、学科素养等, 自适应学习与辅导系统中往往也包含了对能力的判断。问题解决测验的过程数据分析是目前研究最多的测验类型之一, 由于问题解决测验更关注能力的评价, 因此在测量模型的建构上研究也比较丰富, 而其它类型测验在能力评估模型上的创新研究还比较有限。一方面, 问题解决测验过程数据的分析思路对于其它领域测验的数据分析具有借鉴性, 比如以专家系统定义指标的流程大体相同。另一方面, 每种主题的测验都有其特殊性, 如问题解决测验或者学科素养测验更加关注能力的准确估计, 而有些测验则更加关注反应过程, 如批判性思维测验更加关注论证的过程, 因此在借鉴不同领域的分析方法时要视具体情况而定。
李航. (2012).. 北京:清华大学出版社.
李美娟. (2020).(博士学位论文). 北京师范大学.
李美娟, 刘玥, 刘红云. (2020). 计算机动态测验中问题解决过程策略的分析: 多水平混合IRT模型的拓展与应用.,(4), 528–540.
陆璟. (2017).(博士学位论文). 华东师范大学, 上海.
骆文淑, 赵守盈. (2005). 多维尺度法及其在心理学领域中的应用.,(4), 27–30.
王永锋, 王以宁, 何克抗. (2007). 从“学习使用技术”到“使用技术学习”——解读新版美国“国家学生教育技术标准”.,(12), 82–85.
徐伟, 陈光辉, 曾玉, 张文新. (2011). 关系研究的新取向: 社会网络分析.,(2), 499–504.
袁建林. (2018).(博士学位论文). 北京师范大学.
袁建林, 刘红云, 张生. (2016). 数字化测验环境中学生问题解决能力影响因素分析——以PISA 2012为例.,(8), 74–81.
Adams, R., Vista, A., Scoular, C., Awwal, N., Griffin, P., & Care, E. (2015). Automatic coding procedures for collaborativeproblem solving. In P. Griffin & E. Care (Eds.),(pp. 115–132). Dordrecht: Springer.
Adams, R. J., Wilson, M., & Wang, W. C. (1997). The multidimensional random coefficients multinomial logit model.(1), 1–23.
Amer, M. R., Siddiquie, B., Khan, S., Divakaran, A., & Sawhney, H. (2014). Multimodal fusion using dynamic hybrid models. In(pp. 556–563). New York, NY: IEEE.
Arieli-Attali, M., Ou, L., & Simmering, V. R. (2019). Understanding test takers’ choices in a self-adapted test: A hidden Markov modeling of process data., 83.
Bejar, I. I., Mislevy, R. J., & Zhang, M. (2016). Automated scoring with validity in mind. In A. A. Rupp & J. P. Leighton (Eds.),(pp. 226–246). Hoboken, NJ: Wiley-Blackwell.
Bellman, R. (1957). A markovian decision process.(5), 679–684.
Bergner, Y., Walker, E., & Ogan, A. (2017). Dynamic bayesian network models for peer tutoring interactions. In A. A. von Davier, M. Zhu, & P. C. Kyllonen (Eds.),(pp. 249–268). Cham: Springer.
Chen, Y. (2020). A continuous-time dynamic choice measurement model for problem-solving process data.(4), 1052–1075.
Cho, S. J., & Cohen, A. S. (2010). A multilevel mixture IRT model with an application to DIF.(3), 336–370.
Chung, G. K. W. K., Baker, E. L., Vendlinski, T. P., Buschang, R., Delacruz, G. C., Michiuye, J. K., & Bittick, S. J. (2010, April). Testing instructional design variations in a prototype math game. In R. Atkinson (Chair),Poster session presented at the Annual Meeting of the American Educational Research Association, Denver, CO.
Davis, J. A., & Leinhardt, S. (1972). The structure of positive interpersonal relations in small groups. In J. Berger (Ed.),(Vol. 2, pp. 218–251). Boston, MA: Houghton Mifflin.
Friedman, J., Hastie, T., & Tibshirani, R. (2009).[R package version]. Retrieved August 4, 2021, from https://cran.r-project.org/web/packages/glmnet/
Goodfellow, I., Bengio, Y., & Courville, A. (2016).. Cambridge, MA: MIT Press.
Haberman, S. J. (2013).(No. ETS RR-13-32). Princeton, NJ: Educational Testing Service.
Han, Y., Liu, H., & Ji, F. (2021). A sequential response model for analyzing process data on technology-based problem-solving tasks.. Advance online publication. https://doi.org/10.1080/00273171. 2021.1932403
Hao, J., Shu, Z., & von Davier, A. (2015). Analyzing process data from game/scenario-based tasks: An edit distance approach.(1), 33–50.
Harding, S. M. E., Griffin, P. E., Awwal, N., Alom, B. M., & Scoular, C. (2017). Measuring collaborative problem solving using mathematics-based tasks.,(3), 1–19.
He, Q., Borgonovi, F., & Paccagnella, M. (2021). Leveraging process data to assess adults’ problem-solving skills: Using sequence mining to identify behavioral patterns across digital tasks., 104170.
He, Q., & von Davier, M. (2016). Analyzing process data from problem-solving items with N-grams: Insights from a computer-based large-scale assessment. In R. Yigal, F. Steve, & M. Maryam (Eds.),(pp. 749–776). Hershey, PA: Information Science Reference.
Hesse, F., Care, E., Buder, J., Sassenberg, K., & Griffin, P. (2015). A framework for teachable collaborative problem solving skills. In P. Griffin & E. Care (Eds.),(pp. 37–56). Dordrecht: Springer.
Højsgaard, S. (2012). Graphical independence networks with the gRain package for R.(10), 1–26.
Iseli, M. R., Koenig, A. D., Lee, J. J., & Wainess, R. (2010).(CRESST Report 775). Los Angeles, CA: University of California, National Center for Research on Evaluation, Standards, and Student Testing.
Kamata, A., & Cheong, Y. F. (2007). Multilevel rasch models. In M. von Davier & C. H. Carstensen (Eds.),(pp. 217–232). New York, NY: Springer.
Käser, T., Klingler, S., Schwing, A. G., & Gross, M. (2017). Dynamic Bayesian networks for student modeling.(4), 450–462.
Khan, S., Cheng, H., & Kumar, R. (2013). A hierarchical behavior analysis approach for automated trainee performance evaluation in training ranges. In D. D. Schmorrow & C. M. Fidopiastis (Eds.),(pp. 60–69). Berlin: Springer.
Khan, S. M. (2017). Multimodal behavioral analytics in intelligent learning and assessment systems. In A. A. von Davier, M. Zhu, & P. C. Kyllonen (Eds.),(pp. 173–184). Cham: Springer.
LaMar, M. M. (2018). Markov decision process measurement model.(1), 67–88.
Levenshtein, V. I. (1966). Binary codes capable of correcting deletions, insertions, and reversals.,(8), 707–710.
Levy, R. (2019). Dynamic Bayesian network modeling of game-based diagnostic assessments.(6), 771–794.
Levy, R., & Mislevy, R. J. (2016).. Boca Raton, FL: Chapman & Hall/CRC Press.
Liu, H., Liu, Y., & Li, M. (2018). Analysis of process data of PISA 2012 computer-based problem solving: Application of the modified multilevel mixture IRT model., 1372.
Liu, O. L., Mao, L., Frankel, L., & Xu, J. (2016). Assessing critical thinking in higher education: The HEIghtenTMapproach and preliminary validity evidence.(5), 677–694.
Lunn, D., Spiegelhalter, D., Thomas, A., & Best, N. (2009). The BUGS project: Evolution, critique and future directions.(25), 3049–3067.
Ma, W., & de la Torre, J. (2020). GDINA: An R package for cognitive diagnosis modeling.(14), 1–26.
Mayer, R. E., & Wittrock, M. C. (2006). Problem solving. In P. A. Alexander & P. H. Winne (Eds.),(2nd ed., pp. 287–304). Mahwah, NJ: Erlbaum.
Mislevy, R. J. (2019). Advances in measurement and cognition.(1), 164–182.
Mislevy, R. J., Steinberg, L. S., Almond, R. G., & Lukas, J. F. (2006). Concepts, terminology, and basic models of evidence-centered design. In D. M. Williamson, R. J. Mislevy, & I. I. Bejar (Eds.),(pp. 15–48). Mahwah, NJ: Lawrence Erlbaum.
Morency, L.-P., de Kok, I., & Gratch, J. (2010). A probabilistic multimodal approach for predicting listener backchannels.(1), 70–84.
Murphy, K. P. (2001). The bayes net toolbox for matlab.(2), 1024–1034.
Muthén, L. K., & Muthén, B. O. (1998-2015).(7th ed.). Los Angeles, CA: Muthén and Muthén.
Organisation for Economic Co-operation and Development. (2013).. Paris: OECD Publishing.
Organisation for Economic Co-operation and Development. (2017).(Rev. ed.). Paris: OECD Publishing.
Puterman, M. L. (1994).. New York, NY: Wiley.
Raudenbush, S. W., Johnson, C., & Sampson, R. J. (2003). A multivariate, multilevel Rasch model with application to self–reported criminal behavior.(1), 169–211.
Red Hill Studios. (n.d.).Retrieved August 4, 2021, from http://www.pbskids.org/lifeboat
Reichenberg, R. (2018). Dynamic Bayesian networks in educational measurement: Reviewing and advancing the state of the field.(4), 335–350.
Reye, J. (2004). Student modelling based on belief networks.(1), 63–96.
Robitzsch, A., Kiefer, T., & Wu, M. (2020).[R package version 3.5-19]. Retrieved August 4, 2021, from http://CRAN.R–project.org/package=TAM
Rosen, Y. (2017). Assessing students in human-to-agent settings to inform collaborative problem-solving learning.(1), 36–53.
Rowe, J. P., & Lester, J. C. (2010). Modeling user knowledge with dynamic Bayesian networks in interactive narrative environments. In G. M. Youngblood & V. Bulitko (Eds.),(pp. 57–62). Menlo Park, CA: AAAI Press.
Schleicher, A. (2008). Piaac: A new strategy for assessing adult competencies.(5), 627–650.
Shu, Z., Bergner, Y., Zhu, M., Hao, J., & von Davier, A. A. (2017). An item response theory analysis of problem- solving processes in scenario-based tasks.(1), 109–131.
Siddiq, F., Gochyyev, P., & Wilson, M. (2017). Learning in digital networks – ICT literacy: A novel assessment of students’ 21st century skills., 11–37.
Siddiquie, B., Khan, S., Divakaran, A., & Sawhney, H. (2013). Affect analysis in natural human interaction using joint hidden conditional random fields. In(pp. 1–6). New York, NY: IEEE.
Song, Y., & Sparks, J. R. (2019). Measuring argumentation skills through a game-enhanced scenario-based assessment.(8), 1324– 1344.
Tang, X., Wang, Z., He, Q., Liu, J., & Ying, Z. (2020). Latent feature extraction for process data via multidimensional scaling.(2), 378–397.
Tang, X., Wang, Z., Liu, J., & Ying, Z. (2021). An exploratory analysis of the latent structure of process data via action sequence autoencoders.(1), 1–33.
Tang, X., Zhang, S., Wang, Z., Liu, J., & Ying, Z. (2021). Procdata: An R package for process data analysis.(4), 1058–1083.
Technology and Engineering Literacy. (2013).. Retrieved August 4, 2021, from https://nces.ed.gov/nationsreportcard/tel/
VanLehn, K. (2008). Intelligent tutoring systems for continuous, embedded assessment. In C. Dwyer (Ed.),(pp. 113–138). Mahwah, NJ: Erlbaum.
Venables, W. N., & Ripley, B. D. (2002).(4th ed.). New York, NY: Springer.
Visser, I., & Speekenbrink, M. (2010). depmixS4: An R package for hidden Markov models.(7), 1–21.
Vista, A., Care, E., & Awwal, N. (2017). Visualising and examining sequential actions as behavioural paths that can be interpreted as markers of complex behaviours., 656–671.
von Davier, A. A. (2017). Computational psychometrics in support of collaborative educational assessments.(1), 3–11.
von Davier, M., & Lee, Y. S. (2019).. New York, NY: Springer.
Walker, E., Rummel, N., & Koedinger, K. R. (2009). CTRL: A research framework for providing adaptive collaborative learning support.(5), 387–431.
Wasserman, S., & Faust, K. (1994).. Cambridge: Cambridge University Press.
Wilson, M., Gochyyev, P., & Scalise, K. (2017). Modeling data from collaborative assessments: Learning in digital interactive social networks.(1), 85–102.
Wu, M., Adams, R. J., Wilson, M., & Haldane, S. A. (2007).(version 2.0). Camberwell: ACER Press.
Xiao, Y., He, Q., Veldkamp, B., & Liu, H. (2021). Exploring latent states of problem-solving competence using hidden Markov model on process data.(5), 1232–1247.
Yuan, J., Xiao, Y., & Liu, H. (2019). Assessment of collaborative problem solving based on process stream data: A new paradigm for extracting indicators and modeling dyad data., 369.
Zhan, S., Hao, J., & Davier, A. V. (2015). Analyzing process data from game/scenario based tasks: An edit distance approach.(1), 33−50.
Zhan, P., & Qiao, X. (2020). A diagnostic classification analysis of problem-solving competence using process data.. Retrieved August 4, 2021, from https:// doi.org/10.31234/osf.io/wtyae
Zhang, S., Wang, Z., Qi, J., Liu, J., & Ying, Z. (2020).Retrieved August 4, 2021, from http://www.columbia.edu/~zw2393/publication/ process_data_scoring/process_data_scoring.pdf
Zhu, M., Shu, Z., & von Davier, A. A. (2016). Using networks to visualize and analyze process data for educational assessment.(2), 190–211.
Zoanetti, N. (2010). Interactive computer based assessment tasks: How problem-solving process data can inform instruction.(5), 585–606.
Feature extraction and ability estimation of process data in the problem-solving test
HAN Yuting1, XIAO Yue2,3, LIU Hongyun2,3
(1National Center for Health Professions Education Development, Peking University Health Science Center, Beijing 100191, China) (2Beijing Key Laboratory of Applied Experimental Psychology;3Faculty of Psychology, Beijing Normal University, Beijing 100875, China)
Computer-based problem-solving tests can record respondents’ response processes in real time as they explore tasks and solve problems and save them as process data. We first introduce the analysis procedure of process data and then present a detailed description of the new advances in feature extraction methods and capability evaluation modeling commonly used for process data analysis with respect to problem-solving tests. Future research should pay attention to improving the interpretability of analysis results, incorporating more information in feature extraction, enabling capability evaluation modeling in more complex problem scenarios, focusing on the practicality of the methods, and integrating and drawing on analytical methods from different fields.
computer-based problem-solving test, process data, feature extraction, capability evaluation model
B841
2021-08-04
*国家自然科学基金项目(32071091); 国家自然科学基金青年项目(72104006); 北京大学引进人才计划与启动基金(BMU2021YJ010)资助。
刘红云, E-mail: hyliu@bnu.edu.cn
