复合横担杆塔不平衡张力调节装置及其设计方法研究

2022-06-06罗曼平

智慧电力 2022年5期

姜岚，罗曼平，黄力，吴田，唐伟，陈大

（1.三峡大学电气与新能源学院，湖北宜昌 443002；2.湖北省输电线路工程技术研究中心（三峡大学），湖北宜昌 443002；3.中国葛洲坝集团电力有限责任公司，湖北武汉 430034；4.贵州省送变电有限责任公司，贵州贵阳 550002）

0 引言

随着材料技术的发展，针对各行各业所出现的难题，新型材料无疑为解决各类难题提供了新的途径，就输电线路而言，针对其局限性，复合横担杆塔应运而生。复合横担杆塔与传统杆塔相比，其横担采用高强度复合绝缘材料，导线与复合横担端部可直接通过金具相连[1-6]，基于此特点，可减小导线风偏摆动的区间，由此大幅度降低输电走廊，降低土地用量，同时由于复合横担水平布置，可杜绝鸟害，提升防雷、耐污闪、耐雨闪、耐冰闪水平[7-13]。复合横担杆塔具有良好的电气性能和经济性能，但由于复合横担杆塔取消了悬垂绝缘子串，悬垂串的长度将大幅度降低，对于采用分裂导线的高压输电杆塔，其纵向不平衡张力将急剧增加[12，14]，这对复合横担杆塔强度提出了考验，研究表明，纵向不平衡张力主要控制杆塔塔身侧面斜材和塔身横隔面的部分杆件。如果不考虑一定的纵向不平衡张力，就会导致塔身侧面刚度太低，当发生导线断线、覆冰等纵向不平衡张力时，铁塔侧面斜材因承受不了纵向不平衡荷载而倒塔[15]，因此，输电线路不平衡张力问题一直是工程领域关注的重点。

文献[16]分析了2008 年输电线路冰灾倒塔原因，分析得出铁塔倒塌破坏的最主要原因在于导线覆冰过载及其产生过大的纵向不平衡张力。文献[17]通过等线长法原理编制计算程序精确计算了不均匀覆冰条件下杆塔所受的不平衡张力。文献[18]通过有限元法计算线路不平衡张力，并考虑多种因素对线路不平衡张力的影响。文献[19]通过瞬态有限元的方法计算导线脱冰时的不平衡张力，探讨不同脱冰方式下对线路不平衡张力的影响。现有文献主要集中在传统线路不平衡张力的计算与分析方面，而针对复合横担杆塔不平衡张力分析及应对措施方面的研究则未见报道。

针对500 kV 复合横担杆塔，本文设计了一种调节复合横担杆塔不平衡张力的装置，并给出计算模型及算法来计算杆塔在使用装置时承受的不平衡张力，通过对比使用装置前后复合横担杆塔承受不平衡张力大小来验证装置的有效性。

1 不平衡张力调节装置设计

1.1 固定挂点不平衡张力分析

复合横担杆塔宜使用金具成串[20]，但由于取消了绝缘子串使悬垂串长度大大缩短，就500 kV 线路而言，传统铁塔悬垂串长度达到6 m，而其典型300 kN金具串长度仅1.255 m[21]，现针对这2 种串长，设定工况计算直线杆塔承受的不平衡张力，工况参数设置为：档数7 档，档距均为400 m，高差均为0，导线采用4×LGJ-500/45 钢芯铝绞线，线路位于10 mm覆冰区，不均匀覆冰工况为前4 档覆冰100%，后3档覆冰20%[22]。

利用文献17 中的计算方法，计算得到6 m 串长时杆塔承受的最大不平衡张力为5 715.59 N；1.255 m串长时杆塔承受的最大不平衡张力为13 294.25 N，可知，由于串长的大幅度减小，杆塔承受的最大不平衡张力成倍数增长。如果将1.255 m 的金具串应用于500 kV 复合横担杆塔，杆塔设计强度将需大大提高，使成本陡然上升，故提出应对措施意义重大。

1.2 不平衡张力调节装置

传统悬垂型杆塔的悬垂串端点与横担的连接采用固定式挂点，当直线塔两侧出现不平衡张力时，悬垂串向大张力侧倾斜，使大张力侧导线松弛，张力减小，而另一侧张力增大，使直线塔承受的不平衡张力降低，且悬垂串越长，其能够偏移的距离就越大，降低杆塔承受的不平衡张力的效果越好[15]，而复合横担杆塔由于其金具串长度较短，其偏移距离有限，致使复合横担杆塔易承受较大不平衡张力。

现通过在复合横担端部挂点增加1 个滑动装置，将金具串端部与复合横担的连接方式由固定式挂点改为滑动式挂点，通过挂点的滑动距离来补偿复合横担杆塔金具串偏移距离有限的不足，当导线因不均匀覆冰等原因产生不平衡张力时，能够通过挂点的滑动调节以及悬垂串的倾斜来调节杆塔承受的不平衡张力，保障线路安全。装置示意图如图1 所示。

图1 新型滑动式挂点装置装置整体图FIG.1 Overall diagram of new sliding hanging point device

挂点的移动通过轴承在隧道式轨道上滚动实现，金具串、自恢复弹簧与2 个轴承的连接轴同轴心连接，轴承两侧弹簧刚度、长度相等，弹簧的恢复力作用可使当杆塔承受的不平衡张力减小时挂点回到装置中间位置，装置金具间具体连接示意图如图2 所示。

图2 新型滑动式挂点装置局部图FIG.2 Local view of new sliding point device

2 不平衡张力调节装置设计方法

采用滑动式挂点装置后，在计算耐张段连续档不平衡张力时，在经典算法[17，23-26]的基础上，需考虑装置上弹簧刚度、弹簧形变量的影响。

2.1 力学模型

输电线路在架线时各档的水平应力相等，各档的悬垂串均处于铅锤状态，但当气象条件发生变化，如各档覆冰不均匀时，各档的水平应力不再相等，造成悬垂串发生偏移、导线挂点滑动，各档档距随之发生变化，计算示意图如图3 所示。其中，σi为第i档的水平应力；li为耐张段内悬垂串处于中垂位置第i档的档距；Δli为第i档档距的增量；δi为第i基直线杆塔上悬垂串导线悬挂点顺线路水平偏距；λi为第i基杆塔上悬垂串的串长；xi为装置上挂点的水平移动量；h1为悬垂串处于中垂位置时，第1 档导线悬挂点之间的高差；β1为悬垂串处于中垂位置第1 档的高差角。

图3 计算示意图Fig.3 Calculation diagram

由状态方程式可得到第i档档距变化量与第i档一相子导线应力的关系，如式（1）所示：

式中：α，E为导线的温度膨胀系数、弹性系数；tm，σm，Δte，γm分别为导线架线时的气温、相应气温下耐张段内架空线的水平应力、架线时考虑初伸长降低的等效温度、架线时各档的自重比载；t，γi分别为计算不平衡张力时的气温、架线时各档的比载。

杆塔承受不平衡张力时，一相分裂导线挂点的等效受力分析图如图4 所示。其中，Wci为一相子导线作用于挂点的垂向荷载；N为导线分裂数；A为子导线截面积；Gi为第i基杆塔上悬垂串的荷载。

由力矩平衡关系可得式（2）：

Wci计算如式（3）所示：

将式（3）代入式（2）可得第i+1 档子导线的应力可由第i档子导线的应力和悬垂串的偏移量求得，如式（4）所示：

考虑弹簧偏移量得：

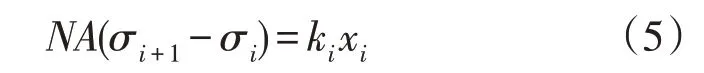
式中：ki为弹簧刚度。

第i基直线杆塔上悬垂串导线悬挂点顺线路水平偏距为：

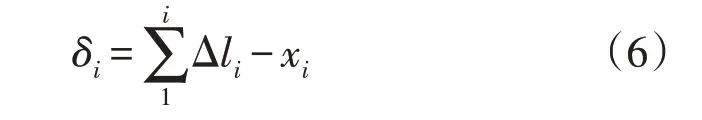
由于耐张段两侧杆塔为耐张塔，故有各档的档距变化量之和为0，即：

耐张段内若有n档，则有n-1 基直线杆塔。利用式（1）可列出n个方程；利用式（4）可列出n-1 个方程；利用式（5）可列出n-1 个方程；利用式（6）可列出n-1 个方程；利用式（7）可列出1 个方程，共可列出4n-2 个方程，有xi，δi，σi，Δli共4n-2 个未知量，可得到求解。

2.2 计算方法

由于式（1），式（4）—式（7）组成的方程组为高元多次非线性方程组，需借助计算机编程求解，对方程组直接求解比较困难，而采用试凑法更加方便快捷且精度较高，试凑法步骤如下：

骤1）重新假定σ1，直至满足式（7）为止。

3 算例分析

本文设计的滑动式挂点装置释放不平衡张力的效果可以通过对比复合横担杆塔在使用装置前后杆塔承受不平衡张力的大小来验证，而由于杆塔承受较大不平衡张力往往发生在不均匀覆冰工况下[16，18，27-29]，故在不均匀覆冰工况下来验证装置的使用效果。

3.1 计算参数

设有500 kV 四分裂线路在某一耐张段的直线塔使用复合横担杆塔，在直线杆塔上使用本文装置，导线采用4×LJG-500/45 钢芯铝绞线，线路处于20 mm 覆冰区，不均匀覆冰工况为前4 档覆冰100%，后3 档覆冰20%[22]，计算气温-5℃，无风，悬垂金具串长度为1.255 m，重量为762 N[21]，子导线安装应力为45.1 MPa，各档具体参数如表1 所示，高差为负值表示该档导线左悬挂点高于右悬挂点。

表1 各档具体参数Table 1 Specific parameters of each span

3.2 结果对比

根据3.1 节参数，分别计算采用传统固定式挂点与采用新型滑动式挂点装置后各复合横担直线杆塔承受的不平衡张力，新装置上的弹簧取多个刚度，不平衡张力计算结果对比如表2 所示（表中编号为直线塔编号，下同，另一种挂点系新装置上的弹簧取3 种刚度）。

表2 2种挂点下各直线塔所受不平衡张力计算结果Table 2 Calculation results of unbalanced tension of linear towers under two kinds of hanging points kN

从表2 可知，承受最大不平衡张力塔为不均匀覆冰的分界塔4，在采用新型滑动式挂点装置后，装置弹簧刚度设置为40 kN/m 时，与固定式挂点相比，分界塔4 的不平衡张力明显降低，降低了约22%，而其他塔的不平衡张力由于装置的调节作用有所增大，但不构成控制条件，说明装置在承受最大不平衡张力的杆塔处作用显著。

新型装置在承受最大不平衡张力杆塔处的效果最明显，而由于装置对不平衡张力的调节作用使得其他杆塔承受的不平衡张力有所增大，因此在各基直线杆塔均采用该装置显然不经济，基于此特点，若只在第4 基杆塔采用装置，并将装置上自恢复弹簧刚度设置为40 kN/m，其他杆塔采用固定式挂点，计算结果与表2 中数据对比如下表3 所示。

表3 2种情况下的不平衡张力Table 3 Unbalanced tension under two cases kN

从表3 可知，若只在承受最大不平衡张力的第4 基塔使用装置，与各直线塔均使用装置相比，第4基塔承受的不平衡张力进一步降低4.5%，而其他塔则有较小幅度升高，且不构成控制条件，因此，建议只在承受最大不平衡张力塔处使用本文设计装置。

新型装置挂点偏移量随弹簧刚度变化如表4所示。

表4 不同弹簧刚度下的挂点偏移量Table 4 Hanging point offset under different spring stiffness m

结合表4 与表2 可知，随着装置弹簧刚度从40 kN/m 增大到80 kN/m，各直线塔挂点弹簧形变量均减小，在承受最大不平衡张力的不均匀覆冰分界塔4，弹簧的形变量降低了0.184 m，使得其承受的不平衡张力增大了3.94 kN，说明装置的效果与弹簧的刚度的负相关性，弹簧刚度越小，弹簧越易发生形变，装置调节杆塔所受不平衡张力的效果越好。