基于有源滤波器自适应阻抗重塑的高速铁路谐波谐振抑制
2022-06-06牛晨,王果,姚俊
牛 晨,王 果,姚 俊
(1.兰州交通大学自动化与电气工程学院,甘肃兰州 730070;2.国网金昌供电公司,甘肃金昌 737100)
0 引言
交-直-交型电力机车作为移动、时变的非线性负载,与牵引网之间存在非线性强耦合关系。在特定频率下,当电力机车的阻抗与牵引网传输线分布电感与电容发生谐振匹配时,将导致牵引网产生谐波谐振,严重威胁电气化铁路的安全运行[1-2]。
针对牵引供电系统谐波谐振机理分析,目前主要有以下三种方法:时域仿真法[3-7]、模态分析法[8-9]和阻抗分析法[10-14]。时域仿真法可以观察车网系统部分或整体的实时变化,在分析不同运行工况的谐波特征等方面十分有效。但时域仿真法无法分析振荡机理,过程比较耗时,并且仿真模型与真实的牵引供电系统存在一定的差距。模态分析法通过计算牵引供电系统网络节点导纳矩阵的特征根,识别谐波谐振的存在并确定其频率,还能准确定位出谐波谐振区域、元件敏感度等。但模态分析法仅仅对牵引网的谐振特性进行分析,并没有考虑到机车的动态特性。阻抗分析法将系统划分为电源和负载子系统并分别进行阻抗建模,用奈奎斯特判据来确定系统的稳定性,可以直观地分析互联系统之间的作用机理和不稳定的影响因素。由于阻抗分析法不需要考虑器件内部结构,只考虑其输入输出特性,系统参数变化时无需重新建模,因此在互联系统中得到了广泛的应用。
谐波谐振抑制是提高系统谐振稳定性的有效方法。牵引供电系统的谐波谐振抑制目前主要有以下几种方法:一、优化牵引网的结构[15]。用改变牵引网的结构,或者改变供电臂的长度等方式,改变牵引网阻抗参数,使系统谐振频率避开输入系统的谐波频率范围,有效抑制谐波谐振。二、加装补偿装置[16-19]。补偿装置主要分为有源滤波器、无源滤波器和混合有源滤波器。有源滤波器的体积小、动态性能好,被广泛应用于电力系统的谐波补偿。但是由于体积的限制,有源滤波器的容量小,其补偿能力有限。无源滤波器安装简单,成本低,容量大,滤波效果好。混合有源滤波器兼顾了无源滤波器和有源滤波器的优点,既满足了良好的动态补偿特性,又增加了容量。三、优化机车变流器的控制策略[20-21]。对机车变流器的控制策略进行优化,减少变流器的输出谐波或消除注入牵引网的固有谐振频率的谐波来抑制谐波谐振。
本文采用阻抗分析法,建立了牵引网、电力机车和有源滤波器的小信号阻抗模型,探究了牵引供电系统的谐振机理;分析了有源滤波器对牵引供电系统谐波谐振的影响。提出了对有源滤波器进行阻抗重塑的牵引供电系统谐波谐振抑制方案,利用虚拟阻抗自适应参数设计提升了虚拟阻抗对动态系统的适应性。最后,在MATLAB/Simulink 平台上搭建了“牵引网-电力机车-有源滤波器”统一仿真模型对该抑制方法的有效性进行验证。
1 统一数学模型建立
在应用阻抗分析法分析牵引供电系统的谐波谐振时,可将车网系统表示为一个“源-负载”阻抗模型,如图1 所示。
图1 中,PCC 为牵引系统并网点,Ztrain为电力机车的等值阻抗,Zs为牵引网的等值阻抗,ZAPF为有源滤波器的等值阻抗。

图1 牵引网—机车等效电路Fig.1 Traction network-locomotive equivalent circuit
在应用阻抗分析法评估系统小信号稳定性问题时,通常将系统分为源和负载子系统,通过源和负载子系统等效阻抗的比值,对系统的稳定性进行判断。因此,需要分别建立牵引网、电力机车与有源滤波器的阻抗模型。
1.1 牵引网-电力机车数学模型
电力机车属于典型的非线性负载,在使用阻抗分析法时需要建立线性阻抗模型。因此,可以利用dq变换将所有变量都变换到固定操作点,再用小信号法对其进行线性化处理[10]。车网系统属于单相交流系统,无法直接进行dq变换。因此,可以通过对电压电流采样信号延迟1/4 周期,从而构造1 组正交的电压电流向量进行dq变换。在电力机车的建模过程中将锁相环和直流电压环忽略,dq坐标下电力机车的等效输入阻抗Ztrain是一个2×2 的矩阵,可表示为:

式中:ΔU为电力机车的输入电压;ΔiL为电力机车的负载电流;Zdd,Zdq,Zqd,Zqq分别为dd,dq,qd,qq轴阻抗。
牵引网可以等效成由阻感支路和电容支路并联而成的RLC 电路,由于存在牵引变压器,在计算网侧阻抗时需要将高压侧的阻抗归算到低压侧。归算后网侧的等效阻抗模型Zs如式(2)所示:

式中:K为牵引变压器变比;Rs,Ls和Cs分别为网侧的等效电阻、电感和电容;s为拉普拉斯算子;ω0为系统角频率。
根据图1,牵引网和电力机车等效阻抗的比值Gs(s) 如式(3)所示:
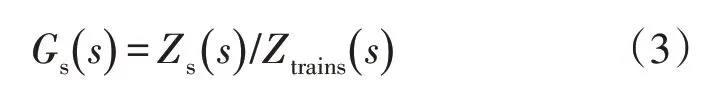
1.2 有源滤波器数学模型
有源滤波器作为非线性电力电子器件,其建模方法与电力机车相同。应用于牵引供电系统的有源滤波器大多采用单相电压源型逆变器,如图2 所示。有源滤波器的电路结构主要是由直流侧电容、逆变器、输出滤波电感组成。其中,us为并网点电压,ua为有源滤波器输入电压,ud为直流侧电压,udref为直流侧参考电压,ic为有源滤波器的输出电流,iL为负载电流,i*为指令电流,L为滤波电感,C为直流侧电容。

图2 有源滤波器主电路Fig.2 Active filter main circuit
根据图2,主电路的输入输出关系如式(4)所示:

式中:Δuad为有源滤波器d轴的输入电压增量;Δuaq为有源滤波器q轴的输入电压增量;Δusd为d轴的并网点电压增量;Δusq为q轴的并网点电压增量;Δicd为有源滤波器d轴的输出电流增量;Δicq为有源滤波器q轴的输出电流增量。
基于瞬时无功理论的单相谐波电流检测原理如图3 所示,将负载电流iL与电网电压同频同相的正余弦sinωt,cosωt分别相乘,构造一对正交分量,然后再进行dq变换提取谐波。

图3 单相谐波电流检测原理图Fig.3 Schematic diagram of single-phase harmonic current detection
图3中,LPF为低通滤波器;PLL为锁相环;为指令电流的d轴分量;为指令电流的q轴分量。
由图3 可知,有源滤波器的输入指令电流i*与电力机车的负载电流相关,考虑到谐波电流检测中的滤波环节以及计算延迟,谐波电流检测环节可以近似看作式(5)所示的一阶惯性环节。即:

式中:kid为补偿系数(0<kid≤1);GCD为谐波电流检测环节的传递函数;Taf为时间延迟。
在dq坐标下,谐波检测模块输出的指令电流与负载电流的关系如式(6)所示:

有源滤波器的控制器主要包括直流电压环(DC Voltage Controller,DVC)和交流电流环(AC Current Controller,ACC)。由于直流电压环仅在低频范围产生影响,而本文仅针对高频的谐波谐振进行分析,因此在建模的过程仅考虑交流电流环的影响,一般交流电流环的控制框图如图4 所示。其中,谐波检测环节检测出来的负载谐波即指令电流信号与滤波器输出的补偿电流信号相比较,利用PI 控制器将比较出来的差值信号进行校正。

图4 交流电流环控制框图Fig.4 AC current loop control block diagram
图4中:Gid(s),Giq(s)分别为d轴和q轴的电流控制器传递函数;icd,icq分别为有源滤波器d轴、q轴的输出电流;uad,uaq分别为有源滤波器d轴、q轴的输入电压;usd,usq分别为d轴、q轴的并网点电压。
由图4 可得有源滤波器的输出电压方程为:
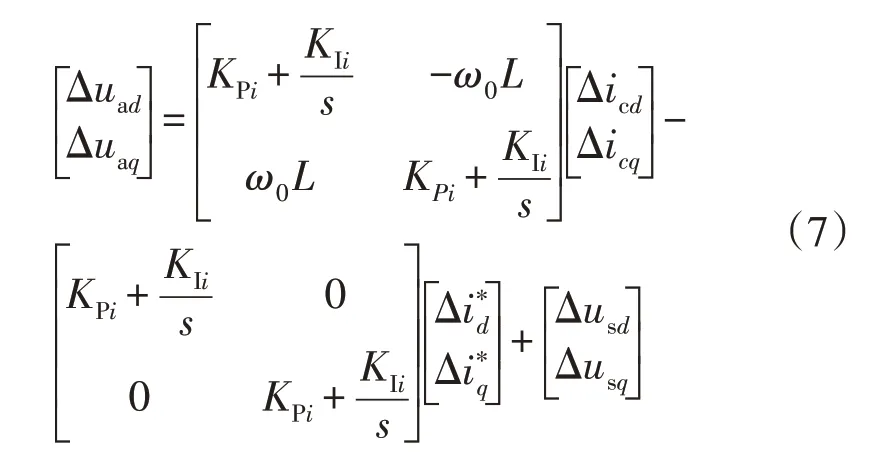
式中:KPi为电流环控制器的比例增益;KIi为电流环控制器的积分增益。
为简化模型,可以将脉冲调制等效为一阶惯性环节Gd(s),如式(8)所示:

式中:kPWM为PWM 增益;Td为时间延迟。
联立式(4)—式(6),可得:

忽略直流电压环的输出信号,得到有源滤波器的小信号阻抗模型ZAPF为:

牵引供电系统在加入有源滤波器后,负载阻抗ZA为:

牵引供电系统中源和负载子系统等效阻抗的比值GA为:

2 牵引供电系统谐波谐振机理分析
牵引网与电力机车发生参数耦合导致的谐振属于谐波不稳定现象[1],根据奈奎斯特稳定判据,系统稳定性主要取决于源和负载子系统等效阻抗比的特征值对(-1,0)点的包围情况。而对于多输入多输出系统,可以用广义奈奎斯特判据进行分析。如果系统源和负载子系统等效阻抗比特征值λ1与λ2的奈奎斯特曲线包围s平面中的(-1,0)点,则系统不稳定;若不包围(-1,0)点,则系统稳定。系统传递函数的参数如表1 所示。

表1 系统参数Table 1 System parameters
根据式(3),假设牵引网的增益为1,仅存在电力机车的阻抗,系统的稳定性如图5 所示。其中,特征值的奈奎斯特轨迹距(-1,0)点较远,负载系统本身处于一个较为稳定的状态。

图5 电力机车的奈奎斯特曲线Fig.5 Nyquist curve of electric locomotive
将牵引网的阻抗代入式(3),对接入电力机车的牵引供电系统的稳定性进行分析,结果如图6 所示。其中,特征值的轨迹包围了s平面的(-1,0)点,系统处于一个不稳定的状态。与图5 相比可知机车系统本身是稳定的,而系统的谐波谐振现象主要是由于机车阻抗与牵引网阻抗的耦合机理引起的。
根据式(12),在保证系统参数不变的前提下,在牵引供电系统中接入有源滤波器,其系统的稳定性如图7 所示。其中,轨迹包围s平面中的点(-1,0),系统依旧处于不稳定的状态,但是与图6 相比,图7 中的特征值轨迹与(-1,0)点的距离更近,系统的稳定性增加。因此,接入有源滤波器可以增加系统的稳定性,抑制谐波谐振。
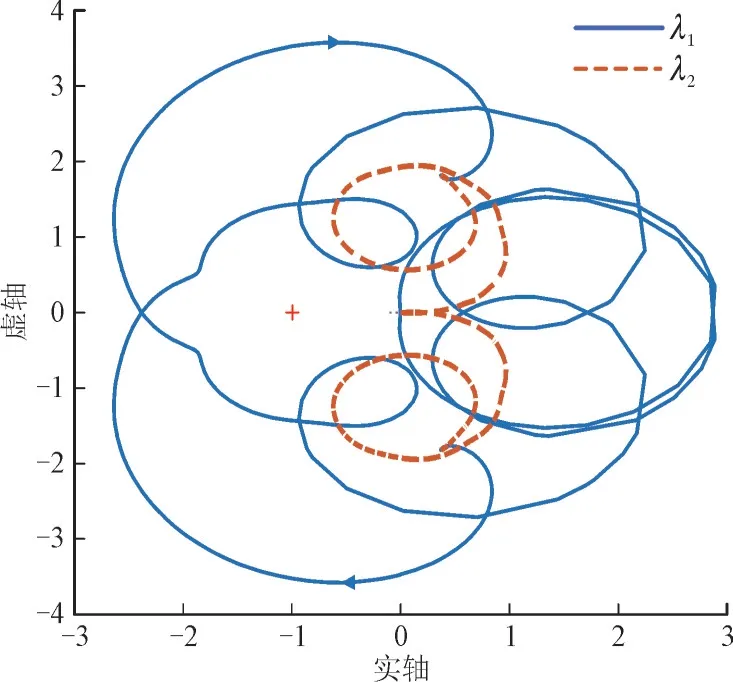
图6 牵引网-电力机车系统的奈奎斯特曲线Fig.6 Nyquist curve of traction network-electric locomotive system

图7 牵引网-电力机车系统的奈奎斯特曲线Fig.7 Nyquist curve of traction network-electric locomotive system
3 有源滤波器等值阻抗重塑
由于有源滤波器可以等效为一个谐波源,其阻抗会对牵引供电系统的谐波谐振和系统的稳定性产生影响。可以通过控制的方法,等效地在有源滤波器上并联一个虚拟阻抗,将有源滤波器的等值阻抗进行重塑,改变系统阻抗参数,抑制系统的谐波谐振[22-25],如图8 所示,其中,红色虚线框内的Rv为虚拟阻抗。


图8 引入虚拟阻抗的电流控制框图Fig.8 Current control block diagram introducing virtual impedance
由图8 中的电流电压关系,结合式(11),引入虚拟阻抗后的有源滤波器的阻抗ZRAPF如式(13)所示:
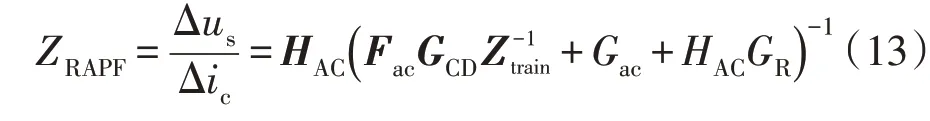
系统的负载阻抗ZRA如式(14)所示:

系统的等值阻抗比GRA如式(15)所示::

式中:Δus为并网点电压增量;Δic为有源滤波器d轴的输出电流增量。
根据式(13),在保证系统参数不变的前提下,在牵引供电系统中接入阻抗重塑后的有源滤波器,其系统的奈奎斯特曲线如图9 所示。由图9 可以看到,其特征值的轨迹并没有包围(-1,0)点,系统处于稳定的状态。由此可知,通过引入虚拟阻抗增加系统阻尼可以有效提高系统稳定性,抑制谐波谐振。

图9 接入阻抗重塑有源滤波器的牵引供电系统奈奎斯特曲线Fig.9 Nyquist curve of traction power supply system connected to impedance reshaping active filter
4 虚拟阻抗自适应参数设计
固定的虚拟阻抗抑制效果是有限的,无法应对牵引供电系统的动态特性。若阻抗值设置过大,则可能抑制效果有限,当系统发生变化时可能导致谐振的发生。若虚拟阻抗参数设置过小,则可能造成有源滤波器端口电流过大,在系统中造成较大的损耗,且对系统的安全运行带来风险[27-28]。因此,需要对虚拟阻抗进行自适应参数设计,来提高其对动态牵引供电系统的适应能力。
牵引供电系统产生谐波谐振时,会造成牵引网电压升高和波形畸变。因此,可以采集牵引网的谐波电压的幅值来衡量谐振的剧烈程度。其控制原理如图10 所示。先提取并网点的电压,经过一个低通滤波器提取基波,再将基波跟并网点电压做减法,得到谐波电压分量。将各次的谐波分量统一表示为:

图10 虚拟阻抗的自适应参数设计控制框图Fig.10 Adaptive parameter design control block diagram of virtual impedance

式中:ush为并网点的谐波电流;Udh为谐波电流的幅值;φdh为谐波电流的相角。
将提取的谐波分量进行平方运算,各次谐波电压的互乘积为交流量,根据式(17)可知,各次谐波电压的自乘积中存在着一个与谐波幅值相关的直流分量和一个交流量,这个直流分量为各次谐波电压幅值平方和,与谐波电压的瞬时值呈正相关。即:

用低通滤波器对上式的直流分量Udh0进行提取,设定一个参考值U*和直流分量进行比较计算误差,将误差送入PI 控制器进行调节,最终输出的信号为自适应的虚拟阻抗值的倒数1v。其中,经过PI 控制器后的信号需要通过一个限幅环节,来确保信号为正。
根据文献[26],电压总谐波畸变率THDu的计算式为:

式中:UI为基波分量。
本文将电压总谐波畸变率设定为5%,则有:

AT 牵引网中使用27.5 kV 的单相交流电,将其代入式(19)可得:

5 仿真验证
为了验证上述方法的有效性,按照表1 中的参数在Matlab/Simulink 中搭建“牵引网-电力机车-有源滤波器”统一仿真模型。
图11 给出的是仅接入电力机车后的接触网电压波形与频谱分析结果。从图中可以看出牵引网在接入电力机车后网压的谐波畸变率较高,THD值为20.94%,谐波主要分布在20 次、40 次和80 次附近,40 次附近的谐波幅值较低。

图11 牵引网电压Fig.11 Traction grid voltage
在牵引供电系统中加入有源滤波器后,接触网电压波形与频谱分析结果如图12 所示。与图11相比可知谐波含量明显减少,THD降到3.33%。20次、40 次与80 次附近的谐波幅值明显降低,而100次附近谐波的幅值有所升高,系统仍存在谐波谐振的问题。

图12 加入有源滤波器后牵引网电压Fig.12 Traction grid voltage after adding active filter
图13 为接入阻抗重塑的有源滤波器后,接触网电压波形与频谱分析结果。与图12 相比可知绝大部分谐波被滤除,THD为1.16%,谐波分布特征不明显,波形基本为标准正弦波。

图13 接入阻抗重塑有源滤波器的接触网电压Fig.13 Overhead cortact voltage of active filter connected to impedance reshapes
图14 为在有源滤波器中加入自适应虚拟阻抗重塑控制策略后的时域仿真图。由文献[14]可知,电力机车电流环比例增益在一定范围内取值越大,系统越稳定。因此,先将电力机车接入牵引网,设置电力机车电流环比例增益的值为7.5。0.5 s 时,将电力机车电流环比例增益的值设置成2.5。从图14 中可以看出,在参数改变后,电力机车四象限变流器的输入电压与输入电流畸变严重,但是牵引网上的电压基本没有变化,保持稳定状态。结果说明加入自适应虚拟阻抗重塑的有源滤波器可以动态的抑制牵引供电系统的谐波谐振,提升系统的稳定性。

图14 虚拟阻抗自适应参数设计仿真波形Fig.14 Simulation waveform of virtual impedance adaptive parameter design
6 结论
针对牵引供电系统的谐波谐振问题,本文基于阻抗分析法建立了“牵引网-电力机车-有源滤波器”的统一阻抗模型,分析了牵引供电系统的谐波谐振机理以及有源滤波器对牵引供电系统谐波谐振的影响,得到如下结论:
1)牵引供电系统中的谐波谐振问题主要是由于车网的阻抗匹配相互耦合引起的,由于牵引网和交直交机车阻抗的固有特性,牵引供电系统的宽频谐振问题无法避免。
2)有源滤波器可以增加系统阻抗,提升牵引供电系统的稳定性,但是并不能满足系统谐振抑制的需求。通过并网点电压前馈的方式等效地给有源滤波器并联一个虚拟阻抗,对有源滤波器进行阻抗重塑,可以改变系统阻抗,进行谐振抑制。同时,自适应参数设计可以提高虚拟阻抗对系统的适应性,进一步增加系统的稳定性。
