基于状态空间法的风机调频退出时刻研究

2022-06-06何廷一陈亦平李崇涛

智慧电力 2022年5期

孙领，何廷一，陈亦平，李崇涛，何鑫，孟贤，和鹏

（1.西安交通大学电气工程学院，陕西西安 710049；2.云南电网有限责任公司电力科学研究院，云南昆明 650200；3.中国南方电网电力调度控制中心，广东广州 510663）

0 引言

风电作为清洁环保和技术成熟的新能源发电技术，已得到广泛的应用[1-2]。据相关统计数据，截至2020 年底，我国风电装机容量已达到2.09 亿kW，占比为12.79%[3]。随着碳达峰与碳中和目标的推进，风电等新能源势必会在新型电力系统中扮演更为重要的角色。然而区别于传统机组，主流的双馈风机和直驱风机依赖于全功率变流器接入系统，缺乏与系统的直接耦合关系。因此，大规模的风电接入也给系统带来了惯量降低和一次调频能力不足的问题，为系统的频率稳定性带来了挑战[4-5]。

为此风电机组也应具备一定的频率调节能力，目前常用的一种控制方式为惯量控制。文献[6]较早提出了惯量控制的概念。文献[7-8]表明风机采用惯量控制时，功率扰动发生后频率的暂态过程可得到有效改善。而风机基于惯量控制参与调频时，转速将偏离最优运行点，这会降低风机对于风能的利用率，同时也不利于风机参与后续的调频任务。因此在参与调频一段时间后，风机需退出调频而进入转速恢复阶段[9]。而风机退出调频将导致系统出现功率的跌落，进而带来频率二次跌落问题。为了减轻风机退出调频对于系统运行的影响，文献[10]采用风机与传统发电机相协调的方式，在风机退出调频时将惯量控制附加功率和转速恢复所需的功率补偿至传统发电机的功率参考值中，使得传统发电机能够尽早调整输出功率来改善频率的动态性能，但所述方法需准确估计所需补偿的功率，否则可能出现频率过调节和振荡问题。文献[11-14]通过风机与储能系统相配合的方式来缓解频率二次跌落问题，而储能系统的配置也增加了额外的投资。文献[15-18]从风机自身角度出发，通过重新设计风机转速恢复过程中的功率参考曲线来实现退出调频时风机功率的平缓降低，但所述方法也延缓了风机转速恢复过程。文献[19-20]提出了风电场中的风机在不同时刻退出的方式来分散风机退出调频对于系统带来的不利影响，而所述方法也增加了风电场内协调控制的复杂性。文献[21]考虑到风机退出调频对于频率的影响，根据一次调频评价指标来确定最佳的退出时刻，但所述方法需借助于简化模型不断试探，缺乏更为直接的求解依据。文献[22-24]根据简化的频率响应模型，通过推导得到了固定的风机调频退出时刻，而研究中风机采用的是方波式的调频策略，未对实际工程中应用较为广泛且更为复杂的惯量控制加以研究。因此，风机采用惯量控制时的调频退出机制仍有待于进一步研究。

针对上述问题，本文基于状态空间法提出了风机调频退出时刻的确定方法。首先由状态空间法推导了研究所需的系统模型。然后以风机调频退出时刻为分界，得到了系统的分段线性化模型，并应用于频率的动态分析。进一步地，以提升频率二次跌落对应的频率最低值为目标，建立了相应的优化模型，并给出了求解算法。最后，通过仿真系统模型验证了本文方法的有效性。

1 系统模型分析

现有文献多集中于火电主导系统的研究，考虑到我国水力资源较为丰富，其中云南、四川等省份水电占比超70%[25]，因此，本文的研究对象为水电主导系统。为了研究的方便，忽略系统中功角和电压的动态过程[26]，主要分析频率问题所涉及的系统模型。

1.1 水电机组模型

在研究电力系统频率稳定性问题时，对于水电机组一般只分析原动机及调速系统模型，且常用的模型框图如图1 所示，忽略了死区的影响。图1 中f和fref分别为系统频率标幺值和频率参考值；KW为频率偏差放大倍数；KP1，KI1和KD1分别为调节系统比例、积分和微分系数；Yref为导叶开度参考值；bP为调差系数；KP2为电液伺服系统比例系数；T1，T2和TOC为时间常数；TW为水锤效应时间常数；Ph为水轮机输出功率标幺值；x1～x7，xD1和xI1为广义状态变量；s为微分算子。

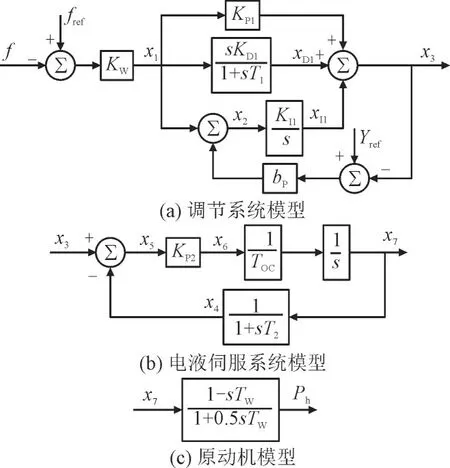
图1 水电机组模型Fig.1 Hydroelectric unit model

根据图1 中的模型，将各广义状态变量改写为增量形式，可得调节系统状态空间表达式为：

电液伺服系统状态空间表达式为：

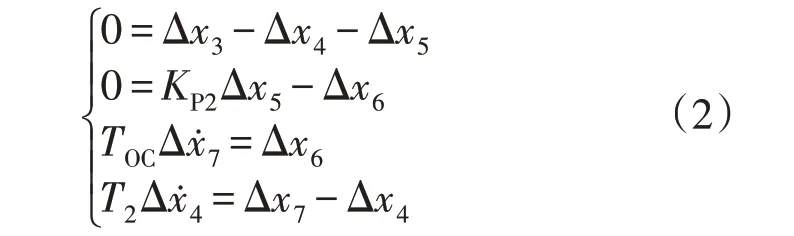
原动机模型的状态空间表达式为：

式（1）—式（3）构成了研究频率问题时水电机组的数学模型。

1.2 风电机组模型

详细的风电机组模型一般包括风力机模型、轴系模型、发电机模型和变流器控制模型等。而风电机组参与系统惯量响应和一次调频时，本质上属于机电暂态过程[27]，影响系统动态行为的主要是与风机转速相关的变量[28]。因此为了便于研究，对于风电机组可采用如下简化模型，即：

式中：Pm为风机机械功率标幺值；ρ为空气密度；R为风轮半径；v为风速；Cp(λ,β)为风能利用系数；λ为叶尖速比；β为桨距角；Pwn为风机额定功率；Pw为风机输出功率标幺值；km为最大功率追踪系数；ω为风机转速；Padd为惯量控制对应的附加功率；kp和kd为惯量控制比例项和微分项系数；Jw为风机转动惯量。

风能利用系数Cp(λ,β)可表征为λ和β的非线性函数，常用的表达式为[29]：

式（4）—式（5）所描述的风电机组模型为非线性模型，为了便于研究，可在平衡点处对其进行线性化处理。设平衡点处的风速v和风机转速ω分别为v0和ω0，不考虑风速和桨距角的变化时，可得到风电机组线性化模型为：

在参与调频一段时间之后，风机将进入转速恢复阶段。以常规的转速恢复过程为例，风机切除惯量控制，从而机械功率和电磁功率之间产生偏差并使得风机加速运行。而这一过程实质上可通过将上述模型中的惯量控制参数kp和kd置零来进行描述。因此，通过改变kp和kd的值即可对风电机组参与调频和转速恢复阶段进行分析。

1.3 频率响应简化模型

电力系统计算中通常采用标幺值，因此需对水电和风电机组进行标幺值折算。这里采用水电机组额定功率Phn与风电机组额定功率Pwn之和作为系统的功率基准值。

水电机组与系统直接耦合，其机组惯量可在系统中直接体现；风电机组通过变流器接入电网，对系统而言，其等效惯量为0。因而对于含有大规模风电机组的系统，需对系统的等效惯性时间常数Hs进行计算。由旋转动能相等的原则，可得Hs的计算式为[15]：

式中：Hh为水电机组惯性时间常数。

同理，系统等效阻尼系数Ds的计算式为：

式中：Dh为水电机组阻尼系数。

在统一功率基准后，可得到系统频率的动态过程，即：

式中：kh为水电占比，且kh=Phn/(Phn+Pwn)；kw为风电占比，且kw=Pwn/(Phn+Pwn)；ΔPd为负荷功率变化量标幺值。

1.4 全系统线性化模型

联立式（1）—式（3）、式（6）和式（9），即可得到全系统的线性化模型为：

式中：T11∈ℝn×n，T12∈ℝn×m，其中n为状态变量个数，m为代数变量个数；Δx为状态变量组成的n维列向量，具体包括ΔPh，ΔxI1，Δx4，Δx5，Δx7，Δω和Δf；Δz为代数变量组成的m维列向量，具体包括Δx1，ΔxD1，Δx2，Δx3，Δx6和ΔPw；J11，J12，J21，J22，d1和d2为相应维数的矩阵；Δu则为输入量，这里取为ΔPd。

2 频率动态过程分析

第1 节中得到了全系统的线性化模型，而为了便于得到解析式，可通过消元法对式（10）进行变换，变换结果为：

式中：Δx和Δu的含义同式（10）；A和b分别为系统矩阵和输入矩阵且A和b的计算式为：

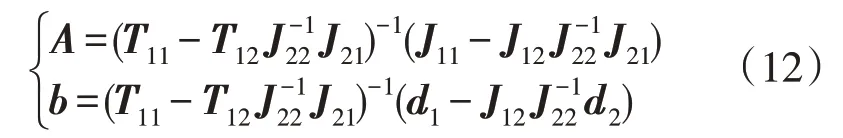
由第1.2 节分析可知，风电机组参与调频和转速恢复阶段的控制参数不同，因而两阶段的矩阵A和b不同。可将式（11）更改为分段线性化模型为：

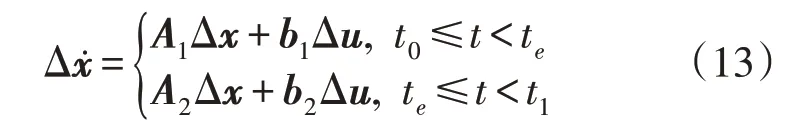
式中：A1和b1为调频阶段对应的矩阵；A2和b2为转速恢复阶段对应的矩阵；t0为负荷扰动出现时刻；te为风机调频退出时刻；t1为所研究的时间范围终点时刻。

2.1 调频阶段频率动态过程分析

根据式（13）可知，风电机组参与调频时，系统线性化方程为：

一般在实际系统中，矩阵A1是可对角化的，即矩阵A1可表示为：

式中：V1为矩阵A1对应的右特征向量矩阵；Λ1为矩阵A1特征值构成的对角矩阵。

在第1 节的分析中，状态变量Δf处于向量Δx中的第n位。则结合上述变量代换过程和式（15）—式（16），可得Δf的表达式为：

对于式（18），可通过牛顿法或二分法求解频率最低值对应的时刻t，并设求解的结果为tn1。出现负荷扰动后，频率会出现多个极值点，因而式（18）实际上是多解的。而在电力系统中，一般在扰动后3～5 s 内频率达到最低值[30]，因而可在该范围内选取方程求解所需的初值。将求解结果代入式（17），即可得到频率最低值fn1。

2.2 转速恢复阶段频率动态过程分析

惯量控制退出后，风电机组进入转速恢复阶段，此时系统线性化方程为：

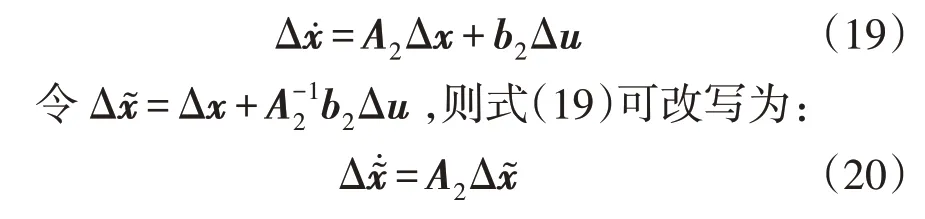
可得转速恢复阶段Δf的表达式为：

系统频率曲线如图2 所示，可知风机退出调频将会带来频率二次跌落问题。在频率最低值处可得：

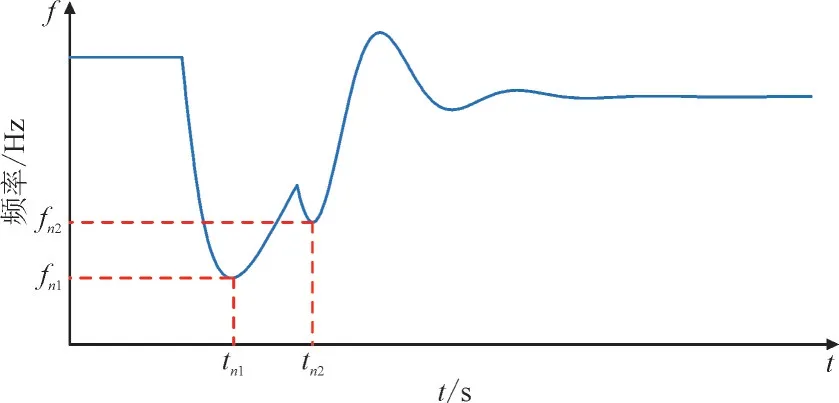
图2 系统频率曲线Fig.2 System frequency curve

与2.1 节类似，求解式（24）即可得到频率二次跌落时频率最低值对应的时刻tn2，将tn2代入式（21）则可得到对应的频率最低值fn2。

3 风机调频退出时刻研究

根据第2 节的分析可知，系统的动态行为以风机调频退出时刻te为界限分为2 个阶段，不同的te将导致频率二次跌落时频率最低值的不同。为了减轻频率二次跌落对系统运行的影响，应合理选择退出时刻，提高频率二次跌落时的频率最低值。因此可建立如下优化模型，其中目标函数为：

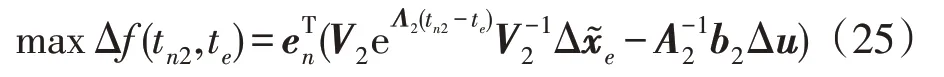
如图2 所示，为了发挥风电机组的调频能力，风机一般在频率越过最低值fn1时才退出调频。结合式（24），可得约束条件为：

针对式（25）和式（26）所述优化模型，这里对其求解方法进行探讨。先不考虑约束条件中的不等式约束而仅考虑其中的等式约束。实质上，等式约束h(tn2,te) 为目标函数Δf(tn2,te) 关于变量tn2的导数。由多元函数取极值的必要条件可知，此时最优解应当满足式（27）方程组：

通过求解式（27），即可得到极值点。而考虑到约束条件中的不等式约束，可通过方程组求解过程中的初值给定环节以及求解结果判断环节来满足该约束，具体分析如下。

由图2 可知，在频率越过最低值fn1之后，若风机较早退出调频，此时频率偏差较大，由式（4）可知风电机组附加功率也较大，因而频率二次跌落问题较为严重；若较晚退出调频，此时风机转速较低，退出调频后系统中的不平衡功率较大，同样会加剧频率二次跌落问题，并且影响了系统的一次调频进程[21]。考虑到实际系统中，一次调频时间一般为10～30 s[15]，因此在求解式（27）时，te的初值可在[tn1+10,tn1+30]区间内选取，并且注意到式（27）的求解结果与Δu无关，因而在求解过程中可令Δu为固定值。具体求解步骤如下，相应的求解流程图如图3 所示。

图3 求解流程图Fig.3 Solution flow chart

5）固定退出时刻。由于步骤2）中在初值区间内未得到符合约束条件的解，或由于步骤4）中判断出求解结果过大，需重新选择退出时刻。为了折中考虑频率二次跌落时频率最低值的提升效果和系统的一次调频时间，可令=tn1+30。

6）输出结果。输出最佳的退出时刻。

通过求解，即可得到风机调频退出时刻，且一般在=tn1+10 时就可得到合理的求解结果。在Matlab 编程环境下，所述求解步骤平均用时为0.013 s，计算速度较快。

4 仿真分析

4.1 模型验证

基于Matlab/Simulink 搭建了仿真系统模型，如图4 所示。系统中G1—G4 为水电机组，母线10 处接入有风电场。系统等效惯性时间常数Hs=3.76 s，等效阻尼系数Ds=0，水电占比kh=0.75，风电占比kw=0.25。

图4 仿真系统模型Fig.4 Simulation system model

为了验证分段线性化模型的准确性，在系统中设置负荷突增扰动。扰动出现时刻t0=20 s，扰动大小ΔPd=0.01 p.u.，而风机调频退出时刻设置为te=40 s。仿真系统模型和分段线性化模型的结果对比如图5 所示，其中仿真系统模型的频率采用的是惯性中心频率。

图5 不同模型结果对比Fig.5 Results comparison of different models

由图5 可知，分段线性化模型的计算结果与仿真系统模型的时域仿真结果较为接近，而在暂态过程中的偏差主要是由风机线性化模型和实际模型之间的差异造成的。系统频率的一些关键量对比情况如表1 所示，其中序号1 表示仿真系统模型的结果，序号2 表示分段线性化模型的结果。

表1 频率关键量对比情况Table 1 Comparison of frequency key variables

通常系统最大频率偏移量不超过0.2 Hz[31]，而由图5 可知，此时系统最大频率偏移量约为0.15 Hz，故所设置的扰动是比较大的。在该扰动下，由表1可知，在tn1和tn2的结果对比中，分段线性化模型与仿真系统模型之间的数值偏差在0.2 s 内；在fn1和fn2的结果对比中，数值偏差在0.002 Hz 内。考虑到频率调节的时间尺度和动态过程，这些偏差均在可接受范围内。因此，所建立的分段线性化模型具有较好的精确度。

4.2 风机调频退出时刻验证

为了验证本文方法得到的风机调频退出时刻的合理性，同样采用4.1 节中的仿真系统模型进行分析。在系统中设置负荷突增扰动，扰动出现时刻t0=20 s，扰动大小ΔPd=0.01 p.u.，由第3 节方法求得最佳退出时刻=43.40 s。则当te取不同值时，频率变化曲线如图6 所示。

图6 不同te取值下频率变化曲线（ΔPd=0.01 p.u.）Fig.6 Frequency variation curve under different te values（ΔPd=0.01 p.u.）

由图6（a）可知，当退出时刻te=时，频率二次跌落现象得到了有效的抑制。由图6（b）可知，当te=时，频率二次跌落时的频率最低值fn2较高。当te＜时，频率最低值fn2会相应地降低，特别是在te=31 s 时，此时风机调频退出时刻较早，导致频率二次跌落现象较为明显。而当te＞时，频率最低值fn2也会降低，且te取值的增加也影响了系统一次调频进程。同时，由图6（b）也可看出，te=31 s时，在频率最低值fn2的结果对比中，分段线性化模型与仿真系统模型之间的偏差较小。这是由于在附近，系统频率已恢复至较高的水平，风机与初始运行点之间的偏离程度相应地缩小，此时风机线性化模型与实际模型之间的偏差较小，因而分段线性化模型和仿真系统模型的结果较为吻合。

综上分析可知，基于本文所述方法得到的风机调频退出时刻是合理的，同时第3 节中也说明了实际上与扰动大小无关。为了进行验证，将扰动ΔPd增加至0.02 p.u.，其余参数不变，当te取不同值时，频率变化曲线如图7 所示。由图7（a）可知，系统最大频率偏移量约为0.3 Hz，故此时的扰动对于系统而言是较大的。当te=时，风机退出调频带来的频率二次跌落现象同样得到了有效抑制。在图7（b）中，仿真系统模型与分段线性化模型之间的偏差较图6（b）有所增加，这是由于扰动较大造成的，然而并未影响到不同te取值下fn2的大小关系。实际上，在第3 节所述求解步骤中，考虑到求解结果与ΔPd的大小无关，因而在求解中令ΔPd=1。而图6 和图7 的仿真结果也验证了这一结论，即在系统参数不变的情况下，扰动大小的变化不影响最佳的风机调频退出时刻。因此，本文所述方法具有良好的适应性，在扰动发生后，无需对扰动大小进行预测，仅由系统参数即可快速确定最佳的风机调频退出时刻。