基于数据驱动的多微电网互联系统分布鲁棒运行优化

李长宇，唐文秀

（东北林业大学机电工程学院，黑龙江哈尔滨 150040）

0 引言

面对国家提出的“碳达峰”和“碳中和”双碳目标，以风、光等新能源为主体，加强数据驱动新能源高效消纳，推进低碳战略、实现低碳经济已成为我国乃至世界发展的大趋势[1]。但是由于风、光等新能源的随机性、间歇性、不确定性等因素给电力系统持续可靠性供电带来了巨大挑战，微电网作为新能源就地消纳和并网远送的主要模式受到广泛关注[2-3]。同时，多个独立微电网互联形成多微电网（Multimicrogrid，MMG）可更好地实现区域能源互补、提高经济效益以及更灵活地进行能源聚合，提供辅助服务[4]。因此，在进行新能源不确定管理的同时，实现MMG 市场与主配市场之间的协调运行优化对多微电网系统运营商（Multi-microgrid Operator，MMGO）和独立系统运营商（Independent System Operator，ISO）来说至关重要[5]。

在分布式电源出力不确定情况下，如何有效做好MMG 系统支撑主配电网系统稳定运行，实现新能源高效消纳有待深入研究。诸多学者多采用了随机优化（StochasticOptimization，SO）方法进行不确定性管理[6-7]，但很难获得SO 需要的不确定变量精确的信息。鲁棒优化（RobustOptimization，RO）利用不确定性集来描述不确定性变量的不确定性，并不考虑概率分布信息的随机性[8]，但RO 关注的是低概率发生的最坏情况，具有较强的保守性。为了克服SO 和RO 方法的不足，更好地结合两种方法的优点，近年来有学者提出了分布鲁棒优化方法（DistributedRobustOptimization，DRO），通过构建模糊集来描述不确定性变量在最坏情况下的概率分布情况，得到最优决策结果[9-10]。DRO 方法相较于SO 方法只需构建包含真实概率分布的不确定集合，在最恶劣概率分布下进行决策，解决了SO 方法需要不确定变量精确的概率分布信息问题；同时DRO方法包含了随机变量一、二阶距信息或者概率密度函数等统计概率信息，降低了决策方案保守性。基于数据驱动的DRO 方法初步应用于季节性储能管理[11]、配电网无功优化和经济调度[12-13]、输电网扩展规划[14]、联合循环机组自调度[15]等方面，但其应用于多区域微电网互联系统运行优化方面鲜有研究。

多微电网互联系统运行是一个多区域动态最优潮流问题，在理想情况下，调控中心可采用集中式方法，通过访问各区域微电网模型和数据实现互联系统潮流最优。但是考虑各个微电网系统内部隐私和自身利益，只能向上层披露非常有限的信息，因此分布式经济调度架构在多微电网互联系统实际运行中更合适。在文献[16]中提出了基于多参数规划的分布式经济调度。为了追求更高的求解效率，在文献[17]的分布式优化问题中采用了分布拟牛顿法。文献[18]基于目标级联分析算法实现了含微网的主动配电系统自主优化运行。文献[19]提出了一种分布式两阶段鲁棒优化的能量不确定性管理框架，并通过交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）实现配电网和微网间的调度优化。但文献[18-19]均未考虑分布式电源出力的不确定性，在实际应用中并不具有鲁棒性。

综上所述，本文在考虑分布式电源出力不确定性管理的同时，提出了基于数据驱动的多微电网互联系统两阶段分布鲁棒运行优化模型：综合考虑多微电网互联系统中能源类型、分布式电源类型以及不同运营商之间的协调，构建基于数据驱动的多微电网互联系统架构；进行分布式电源的不确定性管理，通过对历史数据和最新测量数据的分析，构造局部模糊集，并针对预测误差对两阶段模型进行更新。为保持区域运行的自主独立性，通过ADMM 算法对两阶段模型进行求解，实现在ISO 和MMGO 之间只交换边界信息就可达到最优协调的目标。最后，通过算例分析表明本文所提分层两阶段分布式协调优化算法可较好地实现多个独立微电网与主配电网之间协调运行优化。

1 基于数据驱动的多微电网互联系统运行优化架构及不确定性模糊集

1.1 MMG多层两阶段分布式运行架构

多微电网互联系统各主体设备主要包括风电、微型燃气轮机等分布式设备以及负荷聚合商和储能设备。各个微电网由MMGO 统一协调管理对外参与ISO 调度，对内优先消纳自身服务区域内的分布式电源功率，维持各微电网区域内功率平衡，如图1 所示。

图1 ISO与MMGO两阶段分布式运行架构Fig.1 Two-stage distributed operation architecture of ISO and MMGO

由ISO 与MMGO 构成的两级系统分布式调度机制主要包括2 个阶段：（1）在预调度阶段，MMGO确定各个微电网聚合备用和有功功率需求，其中包括从ISO 购买电量、出售给ISO 的备用电量、各个微电网负荷需求、微电网内部各个分布式电源的基础有功发电量；（2）在实时校正调控阶段，将对实时有功需求与预调度阶段上报需求之间存在的偏差进行实时监测，针对偏差进行实时控制可调度风机、微型燃气轮机及可控负荷等设备的有功功率。

1.2 多微电网系统中不确定性变量样本预处理

Normal Copula 原理被用来对变量的相关性进行建模[20]。记TN为调度时段数，xt,yt和et分别为时段t不确定性变量的实际值、预测值和预测误差，其关系表达式为xt=yt+et,t=1,…,TN。依据该原理，预测误差与预测值的联合分布函数如式（1）所示：

基于式（3）对日前风电功率进行采样，具体步骤如下：

1）根据历史数据获取各时刻真实值和预测值的边缘分布及协方差矩阵。

2）依据最新预测值yt,t=1,…,TN，计算，得到zy。

3）根据式（3）计算得到zx∣zy的期望值和协方差矩阵。

4）对zx∣zy进行采样，得到zx的样本。通 过得到不确定性变量的样本。采样得到的样本集合考虑了时间相关性，因此对预测值的变化具有较强的数据自适应能力，可更准确地描述风电功率的不确定性。

1.3 基于数据驱动的不确定性模糊集

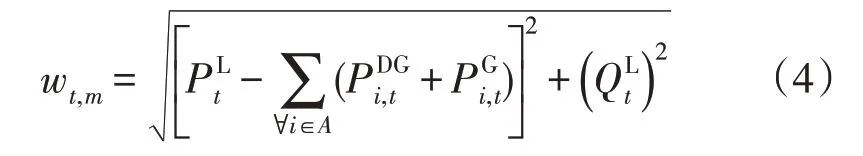
式中：A为微电网m中电源总数；为常规电源有功功率。

本文以Hm,t表示样本集中的样本个数，以[(1-Δ)wm,t,(1+Δ)wm,t] 为界设置聚类分析样本，Δ 为参数。选择的样本通过K-medoids 算法[22]分组到S个场景中，并设置聚类中心点。通过计算某一场景样本数量占总样本数的比率，确定该场景的概率分布为：

综上所述得到概率分布集合，然后构造置信水平为φ的t时段真实概率分布的模糊集为：

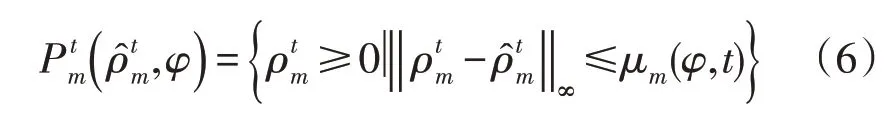
式中：μm(φ,t)为模糊集大小函数，可表示为：

式（7）是由给定的置信水平φ和历史数据的数量Hm,t推导而来。

2 基于数据驱动的多微电网两阶段分布鲁棒优化模型

考虑数据驱动的DRO 两阶段调度优化模型可表示为：

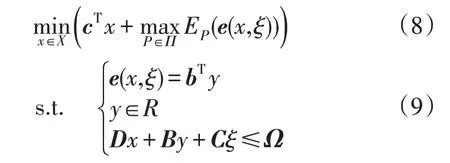
式中：cTx为日前预调度阶段目标函数；EP(·) 为期望值；x为第一阶段决策变量；X为第一阶段决策变量集合；ξ为不确定性变量；y为第二阶段变量；c，b，e，D，B，C，Ω分别为优化模型中与变量相对应的系数矩阵；Π为基于数据驱动的不确定性集合；R为常数集合。

本文主要考虑ISO 与MMGO 互联系统整体经济性，构建两阶段分布鲁棒模型如下：

MMGO 根据日前预调度计划并同时考虑分布式电源出力和负荷功率的不确定性进行实时调控。实时调控优化目标主要以各微电网实时调控成本最优为目标，微电网m实时调控变量主要包括可控电源出力调整量、储能系统充放电调整量，其目标函数为：

式中：ΔCG,UD为常规机组出力调控成本；ΔCESS为储能能充放电调控成本；ΔCEX为MMGO 与ISO 实时交易成本；Closs为实时调控弃风惩罚成本。

两阶段约束条件主要是保证供用电之间的功率平衡、各分布式发电设备出力不越限、各微电网内部线路安全约束及互联微电网交换功率限制等，其约束条件为：

3 模型求解

利用列约束生成算法[23（]Column-and-Constraint Generation，C&CG）将两阶段模型解耦为2 个凸规划问题，即主问题（Master Problem，MP）和子问题（Subproblem，SP）；然后利用ADMM 求解主问题MP，其具体求解过程详见文献[24-28]。

本文利用C&CG 对目标函数式（6）进行求解，并将其写成紧凑矩阵可表示为：

式中：dTy为实时调控阶段目标函数；Θ(x,u)为实时调控目标函数约束集合；u为不确定性量；V，G，H为系数矩阵。

MP 表达式如式（17），SP 表达式如式（18）：

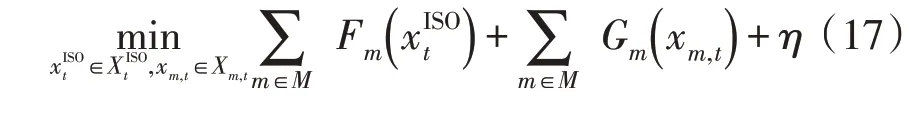
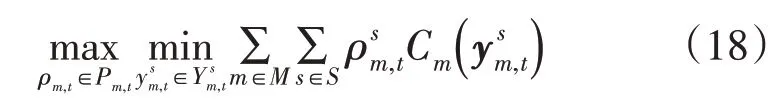
式中：Pm,t为概率分布模糊集合；η为C&CG 中的辅助变量，表示最坏情况概率分布下第2 阶段的期望成本的上限。

C&CG 与ADMM 相结合的分布式算法具体求解步骤如下：

6）更新迭代次数l=l+1，并判断(UB-LB)/UB＞ε？如果大于，转到步骤3）；如果小于，主问题MP 和子问题SP 收敛，程序结束。

4 仿真分析

4.1 算例介绍

改进IEEE33 节点系统分为MG1，MG2，MG3 3个微电网区域，每个微电网内均接入1 个光伏（PV）、1 个风机（WT）、1 个储能（ESS）、1 个可控柴油发电机（MT）。电源设备在系统中的接入情况如图2 所示。电源设备容量配置及节点位置如表1所示，储能设备参数如表2 所示，各设备运维成本如表3 所示。电力交易价格如图3 所示。

图2 多微电网互联系统示意图Fig.2 Schematic diagram of multi-microgrid interconnection system

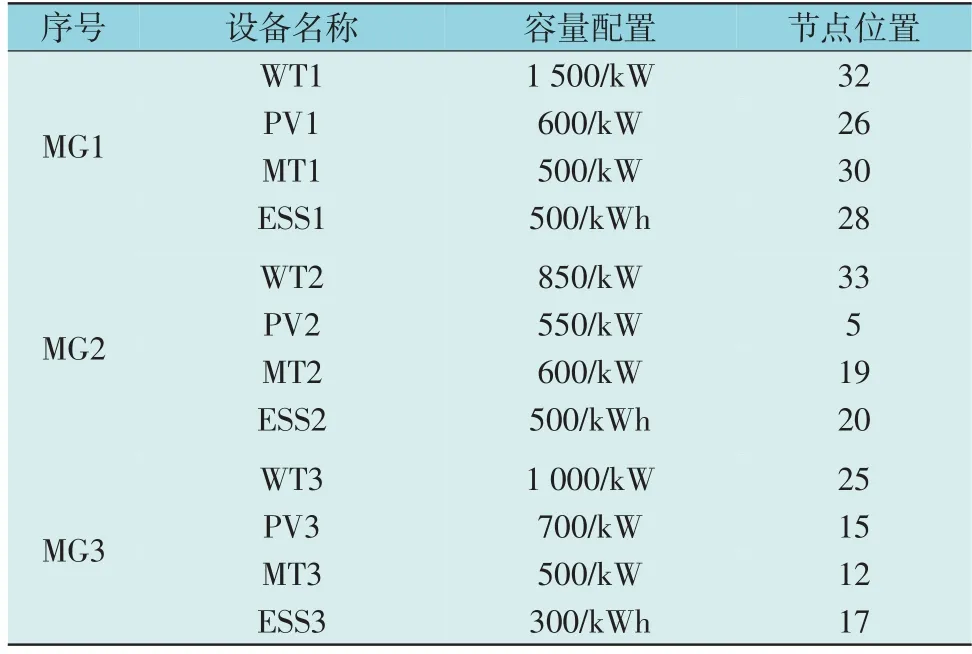
表1 各设备容量配置及接入节点位置Table 1 Capacity configuration and node location

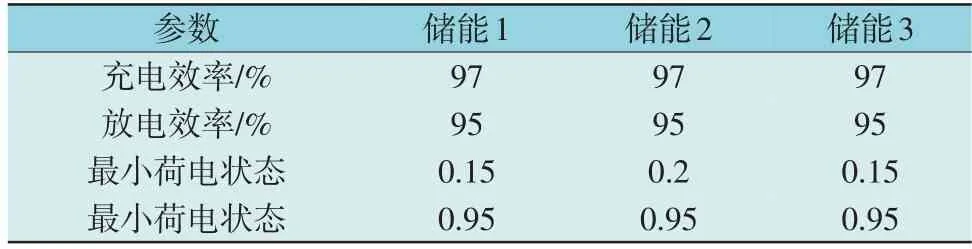
表2 各储能设备参数Table 2 Parameters of each energy storage equipment

表3 设备运维成本Table 3 Equipment operation and maintenance costs

图3 电力交易价格Fig.3 Electricity transaction price

4.2 结果分析

图4 给出了本文C&CG 与ADMM 相结合的分布式算法求解的模型收敛曲线。从图4 可以看出，采用本文算法对MP，SP 进行4 次交互迭代求解后，模型最优化解达到收敛，能较好地满足优化模型求解需求。

图4 模型最优解求解收敛曲线Fig.4 Optimally-solved model convergence curve

图5 给出了MG1，MG2，MG3 中光伏、风机和负荷在最坏概率分布场景下的功率情况。

由图5 可知，在交易电价较高的10:00—17:00时段，每个微电网在最坏概率分布场景下负荷功率要高于实际功率，其主要原因是保证满足负荷需求；其他时段与实际负荷功率接近，在10:00—17:00光伏发电输出功率低于实际值，在00：00—05：00与20：00—24：00 2 个时段内，风力发电的输出功率低于预测值，表明通过本文方法可有效避免在10:00—17:00 用电负荷高峰时段，因可再生能源电源设备不确定性出力变小造成的电压越下限，保证系统在不确定性变量的最坏概率分布场景下仍能安全运行。

图6 给出了每个微电网基于本文方法得到的调度计划。

图6 各个微电网调度计划Fig.6 Scheduling plan for each microgrid

由图6 可知，在00：00—05：00 时段，由于该时段内负荷需求较小，风电多出的功率用来给储能设备充电，MT 提供较少功率，并且该时段内电价较低，可采取从外界购买功率的调度策略。在10：00—20：00 时段，各个微电网MT 出力增加以满足负荷高峰期的需求，储能设备也开始释放功率，在该电价较高阶段增加功率售出来获得经济收益。在21：00—24：00 时段，各个微电网将储能设备充电至初始容量，并且由于该时段负荷需求降低，各个微电网MT出力以及向外售出功率随之减少。

图7 给出了RO 方法、SO 方法与本文方法下微电网预调度成本和实时调控成本对比情况。

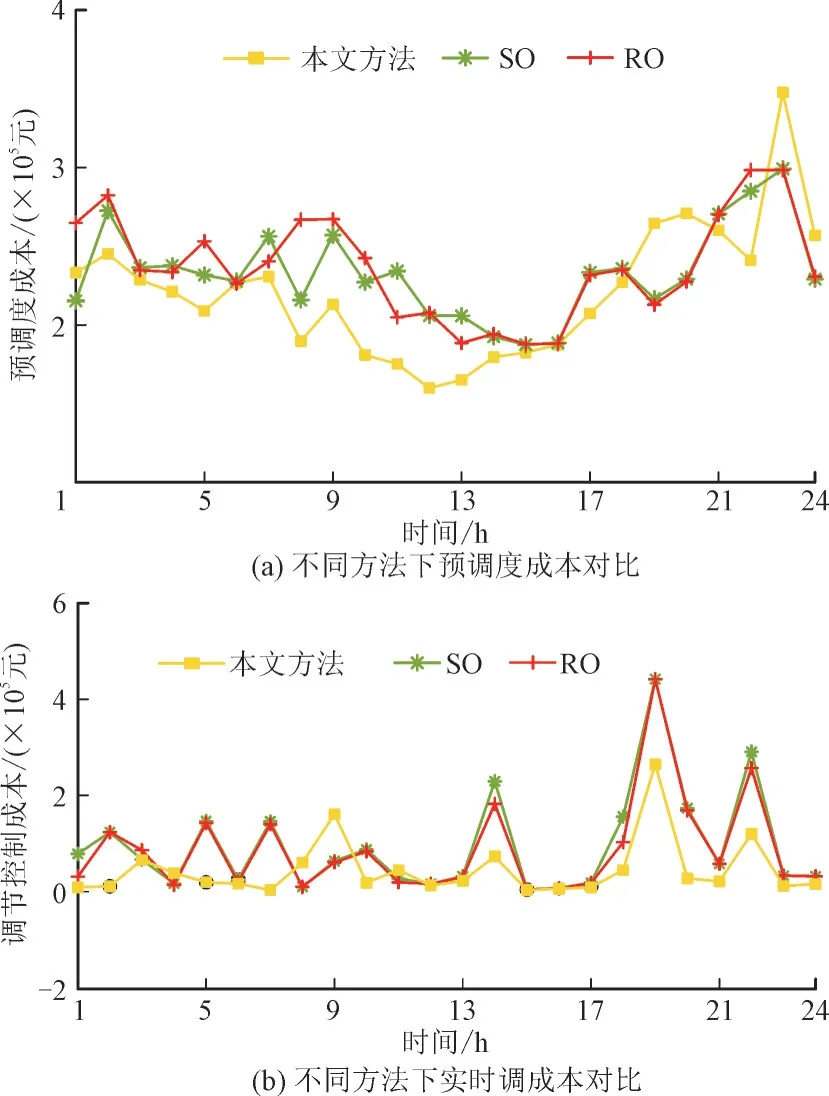
图7 不同方法下两阶段运行成本对比Fig.7 Comparison of two-stage operation cost with different methods

由图7 可知，相较于RO 方法与SO 方法，基于本文方法得到的两阶段成本较少，特别是在02:00，05:00，07:00，21:00，22:00 等时刻；而RO 方法与SO方法较高地估计了负荷功率，导致预调度和实时调控阶段过多地从ISO 购买电量，使得两阶段成本都很高。本文方法较好实现了光伏、风机和负荷不确定性变量的预测，从而有效降低了两阶段的成本。

5 结语

本文提出了基于数据驱动的多微电网互联系统分布鲁棒运行优化策略，利用数据驱动方法，在分布模糊集内构建了一个包含预调度和实时调控两阶段多区域微电网运行优化模型，在不确定变量的最坏概率分布下优化ISO 与多微电网运行总成本。为了保持各个微电网的独立性，提出了一种基于ADMM 和C&CG 结合算法的ISO 与多微电网分解迭代求解方案，并保证了ADMM 和C&CG 结合算法的收敛性。通过将本文方法与SO 方法、RO 方法进行比较，表明了本文方法总体成本最低，系统安全性更高。