对“证明”的认识

李沅骏

七年級下学期我学习了“证明”，知道了证明在数学学习中的重要性。但对于什么是证明，为什么要证明，以及怎样证明，还有许多小伙伴不是很理解。下面，我就来谈一谈我对“证明”的认识，希望能对小伙伴们的学习有所帮助。

“证明”的释义为：用一定材料来表明事物的真实性。在数学学习中，根据已知的真命题，确定某个命题真实性的过程叫作证明。经过证明的真命题是定理。这里还涉及一个概念——“命题”，教材解释是：判断一件事情的句子叫作命题。命题分为真命题和假命题两类。证明用到的命题必须是真命题。

为什么要证明呢？证明是为了用客观事实来判断真伪。在数学学习过程中，通过观察、操作和实验等方式可以探索、发现一些数学结论，但这些结论不一定正确。这就需要我们用数学知识对发现的结论加以证实。只有经过证明的结论才是准确的、科学的。

证明的过程要求言必有据，通常包含几个推理。每个推理应包括因（因为）、果（所以）和由因得果的依据。

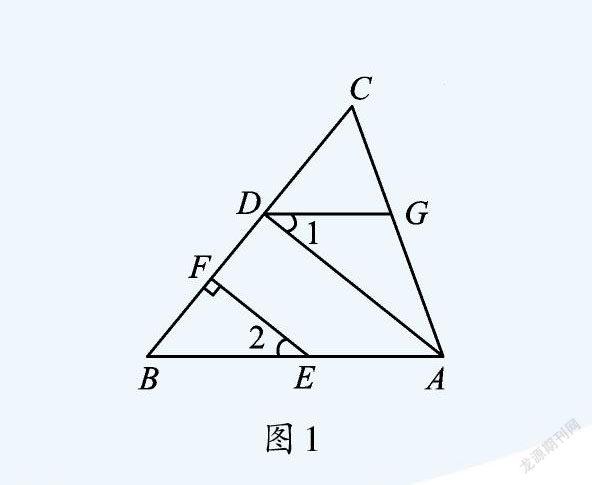
例如，如图1，∠CGD=∠CAB，∠1=∠2，EF⊥BC于点F。求证：AD⊥BC。

证明：∵∠CGD=∠CAB（已知），

∴DG∥AB（同位角相等，两直线平行），

∴∠1=∠DAB（两直线平行，内错角相等）。

又∵∠1=∠2（已知），

∴∠2=∠DAB（等量代换），

∴AD∥EF（同位角相等，两直线平行），

∴∠ADB=∠EFB（两直线平行，同位角相等）。

∵EF⊥BC（已知），

∴∠EFB=90°（垂直的定义），

∴∠ADB=90°（等量代换），

∴AD⊥BC（垂直的定义）。

在证明的过程中，我们主要根据已经学习的定理把“角”的数量关系转换为“线”的位置关系，再通过线的位置关系证明出结论。证明时要注意书写规范，做到每一步证明有因有果、有理有据、逻辑清晰。总之，我们只有了解了证明的定义、证明的目的以及证明的方法，才能更好地完成证明。

教师点评

证明是很有讲究的。如何使证明过程规范合理，有说服力，需要我们去认真研究。小作者结合学习和思考，对证明的认识很到位，值得我们学习。相信他的认识会对同学们的几何学习提供一些帮助。 （指导教师：孙 凯）